
Introduction to Methods of Approximation in Physics and Astronomy PDF
Preview Introduction to Methods of Approximation in Physics and Astronomy
Undergraduate Lecture Notes in Physics Maurice H.P.M. van Putten Introduction to Methods of Approximation in Physics and Astronomy Undergraduate Lecture Notes in Physics Undergraduate Lecture Notes in Physics (ULNP) publishes authoritative texts covering topicsthroughoutpureandappliedphysics.Eachtitleintheseriesissuitableasabasisfor undergraduateinstruction,typicallycontainingpracticeproblems,workedexamples,chapter summaries, andsuggestions for further reading. ULNP titles mustprovide at least oneof thefollowing: (cid:129) Anexceptionally clear andconcise treatment ofastandard undergraduate subject. (cid:129) Asolidundergraduate-levelintroductiontoagraduate,advanced,ornon-standardsubject. (cid:129) Anovel perspective oranunusual approach toteaching asubject. ULNPespeciallyencouragesnew,original,andidiosyncraticapproachestophysicsteaching at theundergraduate level. ThepurposeofULNPistoprovideintriguing,absorbingbooksthatwillcontinuetobethe reader’spreferred reference throughout theiracademic career. Series editors Neil Ashby University of Colorado, Boulder, CO, USA William Brantley Department of Physics, Furman University, Greenville, SC, USA Matthew Deady Physics Program, Bard College, Annandale-on-Hudson, NY, USA Michael Fowler Department of Physics, University of Virginia, Charlottesville, VA, USA Morten Hjorth-Jensen Department of Physics, University of Oslo, Oslo, Norway Michael Inglis SUNY Suffolk County Community College, Long Island, NY, USA Heinz Klose Humboldt University, Oldenburg, Niedersachsen, Germany Helmy Sherif Department of Physics, University of Alberta, Edmonton, AB, Canada More information about this series at http://www.springer.com/series/8917 Maurice H.P.M. van Putten Introduction to Methods of Approximation in Physics and Astronomy 123 Maurice H.P.M.vanPutten Department ofPhysics andAstronomy SejongUniversity Seoul Republicof Korea (SouthKorea) ISSN 2192-4791 ISSN 2192-4805 (electronic) Undergraduate Lecture Notesin Physics ISBN978-981-10-2931-8 ISBN978-981-10-2932-5 (eBook) DOI 10.1007/978-981-10-2932-5 LibraryofCongressControlNumber:2017932117 ©SpringerNatureSingaporePteLtd.2017 Thisworkissubjecttocopyright.AllrightsarereservedbythePublisher,whetherthewholeorpart of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission orinformationstorageandretrieval,electronicadaptation,computersoftware,orbysimilarordissimilar methodologynowknownorhereafterdeveloped. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publicationdoesnotimply,evenintheabsenceofaspecificstatement,thatsuchnamesareexemptfrom therelevantprotectivelawsandregulationsandthereforefreeforgeneraluse. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authorsortheeditorsgiveawarranty,expressorimplied,withrespecttothematerialcontainedhereinor for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictionalclaimsinpublishedmapsandinstitutionalaffiliations. Printedonacid-freepaper ThisSpringerimprintispublishedbySpringerNature TheregisteredcompanyisSpringerNatureSingaporePteLtd. Theregisteredcompanyaddressis:152BeachRoad,#21-01/04GatewayEast,Singapore189721,Singapore To my parents Preface ModernastronomyrevealsanevolvingUniverserifewithtransientsources,mostly discovered—few predicted—in multi-wavelength observations. Our window of observations now includes electromagnetic radiation, gravitational waves and neutrinos. For the practicing astronomer, these are highly interdisciplinary devel- opments that pose a novel challenge to be well-versed in astroparticle physics and data analysis. In realizing the full discovery potential of these multimessenger approaches, the latter increasingly involves high-performance supercomputing. These lecture notes developed out of lectures on mathematical-physics in astronomy to advanced undergraduate and beginning graduate students. They are organizedtobe largely self-contained, starting from basic conceptsand techniques in the formulation of problems and methods of approximation commonly used in computation and numerical analysis. This includes root finding, integration, signal detection algorithms involving the Fourier transform and examples of numerical integration of ordinary differential equations and some illustrative aspects of modern computational implementation. In the applications, considerable emphasis is put on fluid dynamical problems associated with accretion flows, as these are responsible for a wealth of high energy emission phenomena in astronomy. Thetopicschosenarelargelyaimedatphenomenologicalapproaches,tocapture mainfeaturesofinterestbyeffectivemethodsofapproximationatadesiredlevelof accuracy and resolution. Formulated in terms of a system of algebraic, ordinary or partial differential equations, this may be pursued by perturbation theory through expansions in a small parameter or by direct numerical computation. Successful application of these methods requires a robust understanding of asymptotic behavior,errorsandconvergence.Insomecases,thenumberofdegreesoffreedom may be reduced, e.g., for the purpose of (numerical) continuation or to identify secular behavior. For instance, secular evolution of orbital parameters may derive from averaging over essentially periodic behavior on relatively short, orbital peri- ods. When the original number of degrees of freedom is large, averaging over dynamical time scales may lead to a formulation in terms of a system in approxi- matelythermodynamicequilibriumsubjecttoevolutiononaseculartimescalebya regular or singular perturbation. vii viii Preface In modern astrophysics and cosmology, gravitation is being probed across an increasingly broad range of scales and more accurately so than ever before. These observations probe weak gravitational interactions below what is encountered in our solar system by many orders of magnitude. These observations hereby probe (curved) spacetime at low energy scales that may reveal novel properties hitherto unanticipated in the classical vacuum of Newtonian mechanics and Minkowski spacetime. Dark energy and dark matter encountered on the scales of galaxies and beyond, therefore, may be, in part, revealing our ignorance of the vacuum at the lowest energy scales encountered in cosmology. In this context, our application of Newtonian mechanics to globular clusters, galaxies and cosmology is an approxi- mation assuming a classical vacuum, ignoring the potential for hidden low energy scales emerging on cosmological scales. Given our ignorance of the latter, this posesachallengeinthepotentialforunknownsystematicdeviations.Ifofquantum mechanical origin, such deviations are often referred to as anomalies. While they aresmallintraditional,macroscopicNewtonianexperimentsinthelaboratory,they same is not a given in the limit of arbitrarily weak gravitational interactions. Wehopethisselectionofintroductorymaterialisusefulandkindlesthereader’s interest to become a creative member of modern astrophysics and cosmology. Thisbookwouldnothavebeenpossiblewithoutnumerousin-classinteractions that largely shaped the choice of materials and method of presentation. The author gratefullythanksthemanystudentswhoparticipatedinthisdevelopment.Someof this work is supported by the National Research Foundation of Korea under Grant Nos. 2015R1D1A1A01059793 and 2016R1A5A1013277. Seoul, Republic of Korea (South Korea) Maurice H.P.M. van Putten Contents Part I Preliminaries 1 Complex Numbers ... .... ..... .... .... .... .... .... ..... .. 3 1.1 Quotients of Complex Numbers.. .... .... .... .... ..... .. 7 1.2 Roots of Complex Numbers. .... .... .... .... .... ..... .. 8 1.3 Sequences and Euler’s Constant.. .... .... .... .... ..... .. 9 1.4 Power Series and Radius of Convergence .. .... .... ..... .. 13 1.5 Minkowski Spacetime ..... .... .... .... .... .... ..... .. 17 1.5.1 Rindler Observers.. .... .... .... .... .... ..... .. 20 1.6 The Logarithm and Winding Number . .... .... .... ..... .. 24 1.7 Branch Cuts for logZ. ..... .... .... .... .... .... ..... .. 25 1 1.8 Branch Cuts for zp ... ..... .... .... .... .... .... ..... .. 27 1.9 Exercises .. .... .... ..... .... .... .... .... .... ..... .. 29 Reference ... .... .... .... ..... .... .... .... .... .... ..... .. 33 2 Complex Function Theory. ..... .... .... .... .... .... ..... .. 35 2.1 Analytic Functions... ..... .... .... .... .... .... ..... .. 35 2.2 Cauchy’s Integral Formula.. .... .... .... .... .... ..... .. 38 2.3 Evaluation of a Real Integral.... .... .... .... .... ..... .. 42 2.4 Residue Theorem.... ..... .... .... .... .... .... ..... .. 43 2.5 Morera’s Theorem ... ..... .... .... .... .... .... ..... .. 48 2.6 Liouville’s Theorem.. ..... .... .... .... .... .... ..... .. 50 2.7 Poisson Kernel.. .... ..... .... .... .... .... .... ..... .. 51 2.8 Flux and Circulation . ..... .... .... .... .... .... ..... .. 52 2.9 Examples of Potential Flows .... .... .... .... .... ..... .. 55 2.10 Exercises .. .... .... ..... .... .... .... .... .... ..... .. 56 References .. .... .... .... ..... .... .... .... .... .... ..... .. 60 ix x Contents 3 Vectors and Linear Algebra..... .... .... .... .... .... ..... .. 61 3.1 Introduction .... .... ..... .... .... .... .... .... ..... .. 61 3.2 Inner and Outer Products... .... .... .... .... .... ..... .. 63 3.3 Angular Momentum Vector. .... .... .... .... .... ..... .. 63 3.3.1 Rotations.... ..... .... .... .... .... .... ..... .. 64 3.3.2 Angular Momentum and Mach’s Principle ... ..... .. 65 3.3.3 Energy and Torque. .... .... .... .... .... ..... .. 66 3.3.4 Coriolis Forces .... .... .... .... .... .... ..... .. 70 3.3.5 Spinning Top ..... .... .... .... .... .... ..... .. 71 3.4 Elementary Transformations in the Plane... .... .... ..... .. 74 3.4.1 Reflection Matrix .. .... .... .... .... .... ..... .. 74 3.4.2 Rotation Matrix.... .... .... .... .... .... ..... .. 76 3.5 Matrix Algebra.. .... ..... .... .... .... .... .... ..... .. 77 3.6 Eigenvalue Problems . ..... .... .... .... .... .... ..... .. 78 3.6.1 Eigenvalues of Rð’Þ.... .... .... .... .... ..... .. 78 3.6.2 Eigenvalues of a Real-Symmetric Matrix .... ..... .. 79 3.6.3 Hermitian Matrices. .... .... .... .... .... ..... .. 80 3.7 Unitary Matrices and Invariants.. .... .... .... .... ..... .. 83 3.8 Hermitian Structure of Minkowski Spacetime ... .... ..... .. 86 3.9 Eigenvectors of Hermitian Matrices... .... .... .... ..... .. 91 3.10 QR Factorization .... ..... .... .... .... .... .... ..... .. 94 3.10.1 Examples of Image and Null Space .... .... ..... .. 96 3.10.2 Dimensions of Image and Null Space... .... ..... .. 97 3.10.3 QR Factorization by Gram-Schmidt .... .... ..... .. 100 3.11 Exercises .. .... .... ..... .... .... .... .... .... ..... .. 101 References .. .... .... .... ..... .... .... .... .... .... ..... .. 107 4 Linear Partial Differential Equations . .... .... .... .... ..... .. 109 4.1 Hyperbolic Equations. ..... .... .... .... .... .... ..... .. 109 4.1.1 Inhomogeneous Wave Equation (Duhamel) .. ..... .. 113 4.2 Diffusion Equation... ..... .... .... .... .... .... ..... .. 115 4.2.1 Photon Diffusion in the Sun .. .... .... .... ..... .. 121 4.3 Elliptic Equations.... ..... .... .... .... .... .... ..... .. 122 4.4 Characteristics of Hyperbolic Systems. .... .... .... ..... .. 125 4.5 Weyl Equation.. .... ..... .... .... .... .... .... ..... .. 126 4.6 Exercises .. .... .... ..... .... .... .... .... .... ..... .. 129 References .. .... .... .... ..... .... .... .... .... .... ..... .. 131 Part II Methods of Approximation 5 Projections and Minimal Distances ... .... .... .... .... ..... .. 135 5.1 Vectors and Distances ..... .... .... .... .... .... ..... .. 135 5.2 Projections of Vectors ..... .... .... .... .... .... ..... .. 137 5.3 Snell’s Law and Fermat’s Principle ... .... .... .... ..... .. 142
Description:The list of books you might like

The Mountain Is You

Credence

Mind Management, Not Time Management

The Subtle Art of Not Giving a F*ck

Greek Government Gazette: Part 2, 2006 no. 315

Testamento español

Bölüm-10-sunu

Greek Government Gazette: Part 7, 2006 no. 915

Japanese Journal of Pharmacology 1993: Vol 63 Index

Die Kaiserliche Marine während der Wirren in China 1900-1901
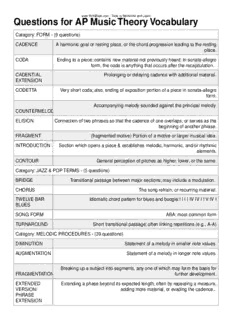
Questions for AP Music Theory Vocabulary

c_paginas INICIAIS_nova.indd

Mary Wares Promised Land by Annie Fellows Johnston

Trocknungstechnik: Die wissenschaftlichen Grundlagen der Trocknungstechnik

DTIC ADA426630: Do We Need An Information Corps? (Joint Force Quarterly, Autumn 1993)

Cytoskeletal Changes of Vitrified Porcine Oocytes

Globalizzazione e decadenza industriale. L'Italia tra delocalizzazioni, «crisi secolare» ed euro

Arthur Gomes Dantas de Araújo PROVAS DE CARGA ESTÁTICA COM CARREGAMENTO ...

Two new species of the genus Gymnomus Loew from Asia (Diptera: Heleomyzidae)

1 AJANTA BULDHANA.cdr

Greek Government Gazette: Part 10, 2009 no. 544

Molecular Evolution of miR-34 Gene Family


