
Preview Robots and Lattice Automata
Emergence, Complexity and Computation ECC Georgios Ch. Sirakoulis Andrew Adamatzky E ditors Robots and Lattice Automata Emergence, Complexity and Computation Volume 13 Series editors Ivan Zelinka, Technical University of Ostrava, Ostrava, Czech Republic e-mail: ivan.zelinka@vsb.cz Andrew Adamatzky, University of the West of England, Bristol, UK e-mail: adamatzky@gmail.com Guanrong Chen, City University of Hong Kong, Hong Kong e-mail: eegchen@cityu.edu.hk Editorial Board Ajith Abraham, MirLabs, USA Ana Lucia C. Bazzan, Universidade Federal do Rio Grande do Sul, Porto Alegre RS, Brazil Juan C. Burguillo, University of Vigo, Spain Sergej Čelikovský, Academy of Sciences of the Czech Republic, Czech Republic Mohammed Chadli, University of Jules Verne, France Emilio Corchado, University of Salamanca, Spain Donald Davendra, Technical University of Ostrava, Czech Republic Andrew Ilachinski, Center for Naval Analyses, USA Jouni Lampinen, University of Vaasa, Finland Martin Middendorf, University of Leipzig, Germany Edward Ott, University of Maryland, USA Linqiang Pan, Huazhong University of Science and Technology, Wuhan, China Gheorghe Păun, Romanian Academy, Bucharest, Romania Hendrik Richter, HTWK Leipzig University of Applied Sciences, Germany Juan A. Rodriguez-Aguilar, IIIA-CSIC, Spain OttoRössler,InstituteofPhysicalandTheoreticalChemistry,Tübingen,Germany Vaclav Snasel, Technical University of Ostrava, Czech Republic Ivo Vondrák, Technical University of Ostrava, Czech Republic Hector Zenil, Karolinska Institute, Sweden About this Series The Emergence, Complexity and Computation (ECC) series publishes new developments, advancements and selected topics in the fields of complexity, computation and emergence. The series focuses on all aspects of reality-based computation approaches from an interdisciplinary point of view especially from applied sciences, biology, physics, or chemistry. It presents new ideas and inter- disciplinary insight on the mutual intersection of subareas of computation, com- plexity and emergence and its impact and limits to any computing based on physical limits (thermodynamic and quantum limits, Bremermann’s limit, Seth Lloyd limits…) as well as algorithmic limits (Gödel’s proof and its impact on calculation,algorithmiccomplexity,theChaitin’sOmeganumberandKolmogorov complexity, non-traditional calculations like Turing machine process and its con- sequences,…) and limitations arising in artificial intelligence field. The topics are (but not limited to) membrane computing, DNA computing, immune computing, quantumcomputing,swarmcomputing,analogiccomputing,chaoscomputingand computing on the edge of chaos, computational aspects of dynamics of complex systems (systems with self-organization, multiagent systems, cellular automata, artificiallife,…),emergenceofcomplexsystemsanditscomputationalaspects,and agent based computation. The main aim of this series it to discuss the above mentioned topics from an interdisciplinary point of view and present new ideas coming from mutual intersection of classical as well as modern methods of com- putation. Within the scope of the series are monographs, lecture notes, selected contributions from specialized conferences and workshops, special contribution from international experts. More information about this series at http://www.springer.com/series/10624 Georgios Ch. Sirakoulis Andrew Adamatzky (cid:129) Editors Robots and Lattice Automata 123 Editors Georgios Ch.Sirakoulis Andrew Adamatzky Department of Electricaland Computer Unconventional ComputingCentre Engineering Universityof theWest ofEngland Democritus University ofThrace Bristol Xanthi UK Greece ISSN 2194-7287 ISSN 2194-7295 (electronic) ISBN 978-3-319-10923-7 ISBN 978-3-319-10924-4 (eBook) DOI 10.1007/978-3-319-10924-4 LibraryofCongressControlNumber:2014951740 SpringerChamHeidelbergNewYorkDordrechtLondon ©SpringerInternationalPublishingSwitzerland2015 Thisworkissubjecttocopyright.AllrightsarereservedbythePublisher,whetherthewholeorpartof the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation,broadcasting,reproductiononmicrofilmsorinanyotherphysicalway,andtransmissionor informationstorageandretrieval,electronicadaptation,computersoftware,orbysimilarordissimilar methodology now known or hereafter developed. Exempted from this legal reservation are brief excerpts in connection with reviews or scholarly analysis or material supplied specifically for the purposeofbeingenteredandexecutedonacomputersystem,forexclusiveusebythepurchaserofthe work. Duplication of this publication or parts thereof is permitted only under the provisions of theCopyrightLawofthePublisher’slocation,initscurrentversion,andpermissionforusemustalways beobtainedfromSpringer.PermissionsforusemaybeobtainedthroughRightsLinkattheCopyright ClearanceCenter.ViolationsareliabletoprosecutionundertherespectiveCopyrightLaw. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publicationdoesnotimply,evenintheabsenceofaspecificstatement,thatsuchnamesareexempt fromtherelevantprotectivelawsandregulationsandthereforefreeforgeneraluse. While the advice and information in this book are believed to be true and accurate at the date of publication,neithertheauthorsnortheeditorsnorthepublishercanacceptanylegalresponsibilityfor anyerrorsoromissionsthatmaybemade.Thepublishermakesnowarranty,expressorimplied,with respecttothematerialcontainedherein. Printedonacid-freepaper SpringerispartofSpringerScience+BusinessMedia(www.springer.com) Preface Robots and Automata are notionally related. In this context, Automata (originated fromthelatinizationoftheGreekword“αυτόµατoν”)asself-operatingautonomous machines,inventedfromancientyearscanbeeasilyconsideredasthefirststepsof these robotic-like efforts. On other words, an Automaton is a self-operating machine, while a robot is a hardware agent with role(s) to operate usually without animmediatehumanoperator.Automataareusefultoolsforformaldescriptionsof robots. Automata themselves are formally represented by final state machines: the abstract machines which take finite number of states and change their state while triggered by certain conditions. Authors of the book bring together concepts, architectures and implementations of Lattice Automata and Robots. Lattice Auto- mataareminimaluniversalinstantiationofspaceandtime.ALatticeAutomatonis either a regular array of finite state machines or collectives of mobile finite state machines inhabiting a discrete space. In both cases the finite states machines, or Automata, update their states by the same rules depending on states of their immediate neighbours. Automata and Robots often share the same notional meaning: Automata are mathematical models of robots and also they are integral parts of robotic control systems. ThebookopenswithinspiringtextbyRosenberg—Chap.1—oncomputational potential of groups of identical finite-state machines. The chapter lays somewhat foundational theoretical background for the rest of the book. Modular robots are kinematic machines of many units capable for changing its topology by dynamically updating connections between the units. To develop efficient algorithms of reconfiguration, we represent the robotic units by configu- rations ofLatticeAutomataandstudyAutomatontransitionrulescorrespondingto reconfiguration. The topic is studied in full details in three chapters: Chap. 2 by Stoy introduces the reader to the theoretical and general aspects of modular reconfigurable robots in Lattice Automata; Chap. 3 by Eckenstein and Yim reproduces all the up-to-date related works and corresponding modular reconfigu- rable robotic systems;whileinChap.4,Tomitaandco-authorsprovidefulldetails forsomeofthesemodular systems,namelyFractumandM-Traninevery possible aspect and discuss the general problems of Lattice-based robotic systems. v vi Preface Motion control and path planning are amongst key problems of robotics, they put high demands on detailed knowledge of environment and consume substantial computational resources. Five chapters explicitly deal with these problems. Thus, Arena and co-authors, in Chap. 5, use Automaton networks to control locomotion of the fly-inspired robot. Efficient ways of routing, an abstract version of path planning, are designed and analysed by Hoffman and Désérable in Chap. 6. Mar- cheseproposestouseparticularfamiliesofCellularAutomatatoprovideanoptimal representation of space and maps in precise parallel motion planning, in Chap. 7. Charalampous and co-authors in Chap. 8 adapt classical designs of Cellular Automaton based shortest path finders to undertake autonomous collision-free navigation. Moreover, Ioannidis and co-authors proposed the employment of Cel- lular Automata advanced with Ant Colony Optimization techniques resulting to CellularRoboticAntssynergycoordinationfortacklingthepathplanningproblem for robotic teams in Chap. 9. Further applications of Lattice Automata in Robotics are presented in the fol- lowingchapters.AnovelmethodofmaprepresentationisproposedinChap.10by Kapoutsis and his co-authors. There, a configuration of elevation heights is con- verted to cells’ states; thus, an entire map is represented by a Cellular Automaton configuration. Cellular Automata have been a classical tool in image processing communitysincemid-1970s,yet,thereisstillvastlandsofunexploredfeaturesand algorithms. In his Chap. 11, Nalpantidis demonstrates practical, real-life imple- mentation of Cellular Automaton algorithms onboard of a mobile robot. The last two chapters deal with cooperative actions in large-scale robotic collectives.Inbothchapters,robotsareoscillatingmechanisms arrangedonatwo- dimensional array: their aim is to adjust their oscillations or states to produce a specifiedvibrationpattern.Silvaandco-authors,inChap.12providemodellingand analysis of the space–time behaviour of such collectives and transitions between different modes of behaviour. Application of the vibrating automaton array to physicalmanipulatorofobjectsinreallifeisstudiedbyGeorgilasandco-authorsin Chap. 13. They show how Automaton model of an sub-excitable medium can be used to purposefully transport objects. All chapters are written in an accessible manner and lavishly illustrated. The book will help computer and robotic scientists and engineers to understand mechanismsofdecentralisedfunctioningofroboticcollectivesandtodesignfuture and emergent reconfigurable, parallel and distributed robotic systems. Georgios Ch. Sirakoulis Andrew Adamatzky Contents 1 Algorithmic Insights into Finite-State Robots. . . . . . . . . . . . . . . . 1 Arnold L. Rosenberg 1.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1.2 Technical Background. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.2.1 FSM “Robots” and Their Domains . . . . . . . . . . . . . . 4 1.2.2 Algorithmic Standards and Simplifications. . . . . . . . . 8 1.3 Mn’s “Walls” as an Algorithmic Tool. . . . . . . . . . . . . . . . . . 9 1.3.1 Algorithms Based on “Bouncing Off” Mn’s “Walls”. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.3.2 Algorithms Based on “Hugging” Mn’s “Walls”. . . . . 15 1.4 The Power of Cooperation. . . . . . . . . . . . . . . . . . . . . . . . . . 21 1.4.1 The Need for Cooperation . . . . . . . . . . . . . . . . . . . . 21 1.4.2 Tasks Enabled by Cooperative Behavior . . . . . . . . . . 23 1.5 Conclusion. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 1.5.1 Retrospective . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 1.5.2 Prospective . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 References. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 2 Lattice Automata for Control of Self-Reconfigurable Robots. . . . . 33 Kasper Stoy 2.1 Self-Reconfigurable Robots . . . . . . . . . . . . . . . . . . . . . . . . . 33 2.1.1 Origin, Features, and Applications . . . . . . . . . . . . . . 35 2.1.2 Mechatronic Implementation . . . . . . . . . . . . . . . . . . 36 2.2 Assumptions of Lattice Automata. . . . . . . . . . . . . . . . . . . . . 37 2.3 Lattice Automata-Based Control. . . . . . . . . . . . . . . . . . . . . . 40 2.4 Hybrid Control. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.5 Conclusion. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 References. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 vii viii Contents 3 Modular Reconfigurable Robotic Systems: Lattice Automata . . . . 47 Nick Eckenstein and Mark Yim 3.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 3.1.1 Motivation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 3.1.2 Key Terminology . . . . . . . . . . . . . . . . . . . . . . . . . . 48 3.1.3 Environments. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 3.2 Challenges and Practical Issues for MRR. . . . . . . . . . . . . . . . 50 3.2.1 General Limitations. . . . . . . . . . . . . . . . . . . . . . . . . 50 3.2.2 Key Metrics. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 3.2.3 Modular Robot Morphology—Shape and Connectedness . . . . . . . . . . . . . . . . . . . . . . . . . 52 3.3 Example Lattice System Hardware . . . . . . . . . . . . . . . . . . . . 52 3.3.1 Key Designs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 3.3.2 Lattice Locomotion. . . . . . . . . . . . . . . . . . . . . . . . . 61 3.3.3 Connection Types. . . . . . . . . . . . . . . . . . . . . . . . . . 63 3.4 Software Systems for MRR . . . . . . . . . . . . . . . . . . . . . . . . . 68 3.4.1 Reconfiguration Planning. . . . . . . . . . . . . . . . . . . . . 68 3.5 Assembly Robotics. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 3.5.1 Self-Assembly and Self-Repair. . . . . . . . . . . . . . . . . 69 3.6 Conclusions and the Future of MRR. . . . . . . . . . . . . . . . . . . 72 References. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72 4 Lattice-Based Modular Self-Reconfigurable Systems. . . . . . . . . . . 77 Kohji Tomita, Haruhisa Kurokawa, Eiichi Yoshida, Akiya Kamimura, Satoshi Murata and Shigeru Kokaji 4.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 4.2 Fractum. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 4.2.1 Basic Design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 4.2.2 Algorithm I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 4.2.3 Algorithm II. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81 4.2.4 Meta Unit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 4.3 3D Units . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 4.3.1 Design. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 4.3.2 Reconfiguration . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 4.4 M-TRAN. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 4.4.1 Design. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 4.4.2 Reconfiguration . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 4.4.3 Robotic Motion . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 4.5 General Problems of Lattice-Based Mechanical Systems . . . . . 90 4.5.1 Improvement in M-TRAN Hardware. . . . . . . . . . . . . 91 4.5.2 General, Physical Problem in Modular Reconfigurable Systems. . . . . . . . . . . . . . . . . . . . . . 91 4.5.3 Achievement by M-TRAN. . . . . . . . . . . . . . . . . . . . 94 4.6 Conclusions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 References. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 Contents ix 5 Speed Control on a Hexapodal Robot Driven by a CNN-CPG Structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97 E. Arena, P. Arena and L. Patané 5.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97 5.2 The Neural Network for Locomotion Control. . . . . . . . . . . . . 99 5.2.1 Leg Motor Neuron Network. . . . . . . . . . . . . . . . . . . 102 5.3 Reward-Based Learning for Speed Control. . . . . . . . . . . . . . . 103 5.4 Dynamic Simulator. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 5.5 Simulation Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 5.6 Conclusions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 References. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115 6 Routing by Cellular Automata Agents in the Triangular Lattice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117 Rolf Hoffmann and Dominique Désérable 6.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117 6.1.1 Cellular Automata Agents . . . . . . . . . . . . . . . . . . . . 118 6.1.2 CA and CA–w Models . . . . . . . . . . . . . . . . . . . . . . 119 6.1.3 Lattice Topology . . . . . . . . . . . . . . . . . . . . . . . . . . 121 6.1.4 The Problem: Routing. . . . . . . . . . . . . . . . . . . . . . . 123 6.2 Minimal Routing in the Triangular Grid. . . . . . . . . . . . . . . . . 125 6.2.1 Topology of S and T. . . . . . . . . . . . . . . . . . . . . . . . 125 6.2.2 Minimal Routing Schemes in S and T. . . . . . . . . . . . 126 6.2.3 Computing the Minimal Route in T (XYZ–Protocol). . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 6.2.4 Deterministic Routing . . . . . . . . . . . . . . . . . . . . . . . 129 6.2.5 Adaptive Routing . . . . . . . . . . . . . . . . . . . . . . . . . . 130 6.3 Modeling the Multi-Agent System . . . . . . . . . . . . . . . . . . . . 130 6.3.1 Dynamics of the Multi-Agent System . . . . . . . . . . . . 130 6.3.2 The CA–w and CA Copy–Delete Rules. . . . . . . . . . . 135 6.3.3 Programming Issues . . . . . . . . . . . . . . . . . . . . . . . . 137 6.4 Router Efficiency and Deadlocks . . . . . . . . . . . . . . . . . . . . . 138 6.4.1 Efficiency of Deterministic Routing . . . . . . . . . . . . . 139 6.4.2 Efficiency of Adaptive Routing . . . . . . . . . . . . . . . . 141 6.4.3 Deadlocks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 6.5 Summary. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 References. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145 7 Multi-Resolution Hierarchical Motion Planner for Multi-Robot Systems on Spatiotemporal Cellular Automata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149 Fabio M. Marchese 7.1 Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149 7.2 MRS Motion Planning Problem . . . . . . . . . . . . . . . . . . . . . . 150
The list of books you might like

The 48 Laws of Power

The Spanish Love Deception

A Thousand Boy Kisses

The Sweetest Oblivion (Made Book 1)

Le Lettere di Giovanni

Trade unions and democracy : Cosatu workers' political attitudes in South Africa

An Introduction to the Theory of Point Processes

By Force of Instinct

Paying Daddy's Debt (Yes, Daddy Book 3)

A NEW SPECIES OF CALLAEUM (MALPIGHIACEAE) FROM PUEBLA, MEXICO

Psychophysics, Second Edition: A Practical Introduction

Manifiesto cubista

The Founding Fathers of American Intelligence

IS 15644: Safety of Electric toys

By Magic Alone

Materials for the Distribution of Lichens in Japan (15) Toninia sedifolia

The Brooklyn Paper Volume 29 Issue 15
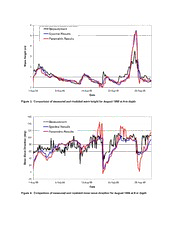
DTIC ADA454270: Incident Boundary Conditions for Wave Transformation

August 2016 PART I

Compressors: Selection and Sizing




