
An Adaptive Modulation Scheme for Two-user Fading MAC with Quantized Fade State Feedback PDF
Preview An Adaptive Modulation Scheme for Two-user Fading MAC with Quantized Fade State Feedback
An Adaptive Modulation Scheme for Two-user Fading MAC with Quantized Fade State Feedback Sudipta Kundu and B. Sundar Rajan Dept. of ECE, IISc, Bangalore 560012, India, Email: sudiptak, bsrajan @ece.iisc.ernet.in { } z ∼CN(0,σ2) Abstract—WithnoCSIattheusers,transmissionoverthetwo- User-1 user Gaussian Multiple Access Channel with fading and finite h1 constellationattheinput,isnotefficientbecauseerrorrateswill 2 be high when the channel conditions are poor. However, perfect x1ǫS1 1 CSI at the users is an unrealistic assumption in the wireless 0 scenario,asitwouldinvolvemassivefeedbackoverheads. Inthis 2 paperweproposeaschemewhichusesonlyquantizedknowledge User-2 y=h1x1+h2x2+z ofCSIatthetransmitterswiththeoverhead beingnominal.The n users rotate their constellation without varying their transmit h2 a J power to adapt to the existing channel conditions, in order x2ǫS2 to meet certain pre-determined minimum Euclidean distance 5 requirement in the equivalent constellation at the destination. Fig. 1: Two-user fading MAC with Gaussian noise 1 The optimal modulation scheme has been described for thecase whenboth theusersusesymmetric M-PSKconstellationsat the ] input, where M = 2λ, λ being a positive integer. The strategy T signal at the destination is thus represented by has been illustrated by considering examples where both users .I useQPSKor8-PSKsignal setsat theinput.It isshownthat the y =√Ph x +√Ph x +z. s proposed scheme has better throughput and error performance 1 1 2 2 c [ coofmapfaereeddbatcokthoevecrohnevaedntoifonjualstnlolno-ga2d(cid:16)apMt8i2ve−scM4he+me2,(cid:17)amt+th1ebciotsst, Wonelyasastutmhee tdheasttipneartfioecnt.CAStIthi.ee.dtehsetitnuaptlieon(hth1,ehs2y)stiesmavcaailnabblee 1 for the M-PSK case. viewed as a single user AWGN channel with the symbols v drawn from a sum constellation 8 8 I. INTRODUCTION =√Ph +√Ph 0 Ssum 1S1 2S2 3 Amultipleaccesschannel(MAC)consistsofmultipleusers =√Ph ( + h2 ) 1. transmittingindependentinformationtoacommondestination. 1 S1 h1S2 0 Thereis no cooperationamongthe users. The capacityregion =√Ph ( +γejθ ), (1) 1 1 2 2 for a discrete memoryless MAC is well known [1] [2]. For a S S 1 two-user MAC with additive white Gaussian noise (AWGN) eff S iv: tphheabceatp.aTcihtey tawcoh-ieuvsienrgGianupsustiains MtheACconwtiitnhuofiunsiteGainupssuitancoanl-- where γ = |hh21|, θ = ∠hh21 |and S{ezff deno}tes the effective X constellation. stellations like M-QAM, M-PSK was studied in [3] [4]. It r was shown that relative rotation between input constellations Without loss of generality it can be assumed that γ 1, a ≥ [3], or a constellation power allocation scheme [4] may be as destination has knowledge of both h1 and h2 separately. employed to maximize the constellation constrained (CC) If h2 < 1, then at the destination the ratio can be simply |h1| capacity regions. Trellis based coding schemes were also reversed to compute h1. Which one among the two ratios h2 suggested to achieve any rate pair within the CC capacity is calculated is made known to the users via a single bit of region. feedback.Fortherestofthepaper,weassumethattheratio h2 h1 In this paper, a two-user MAC with quasi-static fading is calculated at the destination. However, the results obtained is considered, as shown in Fig. 1. The two users transmit stillholdwhentheratiocalculatedis h1,byinterchangingthe h2 information to a common destination. The random variables roles of User-1 and User-2. For the rest of the paper a M- h and h are the channel gains for User-1 and User-2 PSK constellation refers to a symmetric PSK signal set, with 1 2 respectively and h ,h (0,1), where (0,s) denotes M =2λ,λbeingapositiveinteger.ThepointsintheM-PSK 1 2 the circular symmetric∼coCmNplex GaussianCrNandom variable signal set are of the form ej(k−M1)2π, where 1 k M. ≤ ≤ with variance s. AWGN z gets added to the received signal We assume that = = , where is an M-PSK 1 2 S S S S at the destination, z (0,σ2). User-i transmits a symbol constellation. We refer to the pair (γ,θ) to represent γejθ ∼CN x from a complex finite constellation (like M-QAM or and call it the fade state throughoutthe paper.We refer to the i i M-PSK) of unit average energy, i.e, E[S x 2] = 1. Let P complex plane that represents γejθ with γ 1 as the (Γ,Θ) i | | ≥ be the average power constraint for each user. The received plane. Perfect channel state information (CSI) is available at the the two points (s ,s ) and (s ,s ) , where (s ,s ) , 1 2 sum ′1 ′2 sum 1 2 sum destination only, which quantizes the (Γ,Θ) plane into finite (s ,s ) refer to the points√Ph (s +γejθs ) and ′1 ′2 sum ∈Ssum 1 1 2 number of regions. The quantization obtained is similar to √Ph (s +γejθs ) respectively with s ,s ,s ,s . It is 1 ′1 ′2 1 2 ′1 ′2 ∈S the one used for physical layer network coding in [5], which given by was subsequently derived analytically in [6]. This quantized knowledge of the fade state is made available to the users to d′(2s1,s2)sum↔(s′1,s′2)sum =P|h1|2|(s1−s′1)+γejθ(s2−s′2)|2 adapt their modulation scheme via rotation of constellations =P h 2d2 , (2) to compensate for the possibly bad channel conditions. MAC | 1| (s1,s2)↔(s′1,s′2) where (2), d2 denotes the distance between the with limited channel state information at transmitter (CSIT) points (s ,s()s1a,sn2d)↔((ss′1,,ss′2)), where (s ,s ),(s ,s ) refers to has been studied from an information theoretic point of view 1 2 ′1 ′2 1 2 ′1 ′2 the points s +γejθs and s +γejθs in . Since P h 2 in [7], [8]. In [9], it was shown that for a two-user discrete 1 2 ′1 ′2 Seff | 1| simply scales the distances in we can focus only on memoryless MAC with additional common message, finer eff S CofSIoTurreksnuoltwsleindgien,creexapsliincgittmheodcualpaatcioitny srcehgeiomne.sTwoitthhefibneitset d2(s1,s2)↔(s′1,s′2) =|(s1−s′1)+γejθ(s2−s′2)|2 (3) constellations and quantized fade state feedback has not been as the quantity of interest. reported before. It is clear from (3) that for certain values of (γ,θ) the The contributions and organization of this paper are as distance between points (s1,s2) and (s′1,s′2) in Seff reduces follows: to zero, i.e. if A quantization of the (Γ,Θ) plane is derived, for the (s s ) • γejθ = 1− ′1 (4) case when both users use M-PSK constellations at the −(s s ) 2− ′2 input. We illustrate the quantization procedure by taking then d2 = 0. These values of (γ,θ) are called examples of the QPSK and 8-PSK case. (Section II-B) the sin(gsu1,lsa2r)↔fa(ds1e′,sst2a′)tes [5], [6]. Singular fade states can also A modulation scheme is proposed for the users, which • be defined as follows: adaptsaccordingtothequantizedfeedbackaboutthefade state that they receive from the destination, in order to Definition 1: A fade state (γ,θ) is said to be a singular satisfy a certain minimum distance guarantee δ in fade state if eff <M2. eff |S | given in (1). The fade states which leads to violationSof Clearly, γejθ =0 is a singular fade state, for any arbitrary signal set . For any input constellation the other non-zero this minimum distance guarantee have been identified. S S singular fade states are obtained using (4). For a given input Adaptation involves rotation of the constellation of one constellation ,let denotethesetofallsingularfadestates. user relative to the other, without any change in transmit S H power, in order to effectively avoid these bad channel conditions. (Section III-A) Example 1: When = = , where is a QPSK 1 2 S S S S Theproceduretoobtaintheoptimalanglesforrotationis constellation, then the non-zero singular fade states are at • stated for the M-PSK case. The optimal rotation angles γ =√2, θ =45 ,135 ,225 ,315 are calculated in closed form for the QPSK and 8-PSK ◦ ◦ ◦ ◦ case. (Section III-B) γ =1, θ =0◦,90◦,180◦,270◦ An upper bound on δ, i.e., the maximum value of the 1 • minimum distance in the effective constellation that can γ = √2, θ =45◦,135◦,225◦,315◦ be guaranteed, is derived. (Section III-C) Since for an AWGN channel the error performance at the Simulation results are presented to show the extent to • destinationisdominatedbytheminimumdistanceoftheinput whichtheproposedstrategyoutperformstheconventional constellation, it is sufficient to study the minimum distance transmission scheme without adaptation. (Section IV) of . Also from Definition 1 minimum distance in eff eff S S II. CHANNEL QUANTIZATIONFORM-PSK SIGNAL reduces to zero at the singular fade states. The following SETS lemma provides an upper bound on the minimum distance of the effective constellation . In this section we obtain a quantizationof the (Γ,Θ) plane Seff into finite number of regions at the destination. Lemma 1: When both the users use any arbitrary signal set (which includes M-PSK, M-QAM) at the input, then A. Distance Distribution in the effective constellation S for any fade state (γ,θ), the minimum distance d (γ,θ) min Without loss of generality we assume that the average between any two points in is upper bounded by the eff power constraint of each user is P = 1. It is known minimum distance in the inpuSt constellation d ( ). min that the error performance for an AWGN channel is deter- Proof: From the definition of d2 (γ,θ), we hSave, min mined by the Euclidean distance distribution of the input constellation. In our case, the distance distribution of d2min(γ,θ)= min |(s1−s′1)+γejθ(s2−s′2)|2 Ssum (s1,s2)6=(s′1,s′2)∈S2 doefc(idγe,sθ)th,ede′(2srr1o,sr2)psuemr↔fo(rsm′1,as′2n)csuematdtehneotdeessttihneatidoins.taFnocreanbyetvwaeluene (s≤1,s2)6=m(si′1n,s′2)∈S2(cid:8)|s1−s′1|2+γ2|s2−s′2|2(cid:9) Now d2min(γ,θ)≤ min |s1−s′1|2 =d2min(S). (5) FromLemma2,itisclearthatwhenbothusersuseM-PSK s16=s′1∈S signalsets, if (γ′,θ′) is a singular fade state, then there exists Also d2min(γ,θ)≤s26=msi′2n∈Sγ2|s2−s′2|2 =γ2d2min(S). (6) sbiencgauulsaer fdaidsteansctaetedsisattri(bγu′t,ioθn′+inp2Mπ),iwshpeerreio1di≤c wpi≤thMper−io1d eff S 2π. The distance distribution of is the basis for channel From (5) and (6), and using the fact that γ ≥1, we have M Seff quantization. Also from Lemma 2, it suffices to obtain such d2 (γ,θ)≤min{d2 (S),γ2d2 (S)}=d2 (S). min min min min a quantization only for the wedge [0,π/M]. This can then be reflected alongthe θ =π/M line, to givethe quantizationfor the wedge [0,2π/M], which when repeated for the remaining Inthefollowinglemma,itisprovedthatinordertostudythe M 1 wedges will cover the entire (Γ,Θ) plane. distanceprofilein eff itissufficienttoconsiderθ [0,π/M] − S ∈ when bothusers use M-PSK signal sets. Distance profilesfor B. Channel Quantization for the M-PSK case other values of θ can be obtained from θ [0,π/M]. We In this subsection we propose a technique to obtain the ∈ use the term wedge [θ ,θ ] to denote the region γ 1 and 1 2 ≥ quantization of the (Γ,Θ) plane, when both users use M- θ [θ ,θ ] on the (Γ,Θ) plane. The lines θ =θ and θ =θ ∈ 1 2 1 2 PSKsignalsets.FromLemma1,whenbothusersuseM-PSK forγ 1andthearcγ =1forθ [θ ,θ ]formtheboundary 1 2 signal sets at the input, the minimum distance in for any ≥ ∈ eff of the wedge [θ ,θ ]. S 1 2 value of (γ,θ), d (γ,θ) d ( ) = 2 1 cos(2π) . min ≤ min S − M Lemma 2: To study the distance profile in Seff when both Now the following lemma gives the numbqer o(cid:2)f singular fad(cid:3)e theusersuseM-PSKconstellations,itissufficienttoconsider states in the wedge [0,π/M]. the case 0 θ π/M. All other cases can be obtained from ≤ ≤ Lemma 3: When both users use M-PSK signal sets at this. the input, the number of singular fade states in the wedge Proof: The proof is in two steps. First we show that the [0,π/M], is given by M2 M +1. Further, these singular distance profile is a repetitive structure with period 2π/M. 8 − 4 fade states lie along the two lines θ =0 and θ =π/M. Next,itisshownthatwithinthewedge[0,2π/M]thedistance Proof: From [6], the total number of singular fade states profile is symmetric about the bisector of this wedge i.e., the other than zero is M3 M2 +M. Out of these, M lie on the θ =π/M line. We have from (1), 4 − 2 circleγ =1.Itisalsoknownfrom[6],thatifγejθ isasingular eff = +γejθ . fade state, then γ1e−jθ is also a singular fade state. Thus, half S S S ofthetotalnumberofremainingsingularfadestateslieinside For any arbitrary value of θ = kM2π +θ′ where k ∈ Z, 0 ≤ the circle γ = 1 and the other half lies outside it. This along θ′ < 2Mπ, with the fact thatsingular fade states are periodic,impliesthe numberofsingularfadestatesforthewedge[0,π/M],isgiven Seff =S+γejθ′(Sej2Mkπ) by = +γejθ′ . S S 1 M3 M2 M2 M 4 − 2 +M = +1. The last equality follows from the fact that rotating a M- M 2 ! 8 − 4 PSK constellation by an integral multiple of 2π/M does not alter the distance profile of the constellation. Thus, whatever Also from[6], it is clear thatthese fade states lie alongθ =0 distanceprofilesfor areobtainedforthewedge[0,2π/M], and θ =π/M lines. eff itisexactlyrepeatedSfortheremainingM 1wedgestocover Wedenotethissetofallsingularfadestateslyinginthewedge the entire range of θ. − [0,π/M] by W. Let NW = W . H |H | To show that the distance profiles are symmetric about Observe from (3), that the distance between two points in θSpr+o=fiγleejsπ(./MπWM−eα,h)wSav,eewnheeerde0to≤sαho≤wπt/hMat,hSav+etγheejs(aMπm+eαd)iSstaanncde Sbφejeftfw=iese∠na(tshfjuen−ecltesiom′jn)enfootfsroγjf=athned1p,θa2.i.rLN{e(otsw1|△,fsrs2oj)m|,(=s(′13,)|s,s′2jt)h}−e∈dsi′jSs|te2affanncisde S+γej(Mπ−α)S ==S++γγee−j(jMπ(Mπ−+α)α()Se.−M2π) (7) d2(s1,s2)↔(s′1,s′2)=|△s1|2+γ2|△s2|2+2γ|△s1△s2|cos(θ+φ2−(φ81)). S S Consider another other pair (sˆ ,sˆ ),(sˆ ,sˆ ) 2 with The first equality is because S = Sejk2π/M, i.e. rotating S sˆ , sˆ , sˆ , sˆ ,andlet sˆ{ =1 sˆ2 sˆ′1 a′2nd}φˆ∈=Se∠ff(sˆ by 2kπ/M gives the same constellation. Thus for k = 1, 1 ′1 2 ′2 ∈S |△ j| | j− ′j| j j− = e−M2π. Also due to the symmetric nature of M-P−SK sˆ′j) for j = 1, 2. If |△sˆ1| = |△s1|, |△sˆ2| = |△s2| and S S φˆ φˆ = φ φ or φˆ φˆ = π (φ φ ), then from constellation,thedistancedistributionofthesumconstellation 2 1 2 1 2 1 2 1 − − − − − (8), d2 =d2 for all values of (γ,θ), dineppuetndcsonosntelyllaotinontsh.eTrheulastive+anγgelβe ofanrodtatio+nγbeetwβeenhathvee even t(hsˆ1o,usˆ2g)h↔t(hsˆe′1,sˆv′2a)lue o(fs1th,si2s)↔di(sst′1a,ns′2c)e changes with (γ,θ). − S S S S same distance profiles, for any β [0,π]. This together with Definition 2: A distance class denoted by , is a subset of ∈ C (7) proves the second part of the lemma. 2 , which contains the pairs of the form (s ,s ),(s ,s ) , Seff { 1 2 ′1 ′2 } Fig. 2: constellation, when both users use QPSK signal sets, for (γ,θ) = (2,14 ). In the figure d stands for the class eff ◦ i S distance function d (γ,θ). Cki (s ,s ) = (s ,s ) where (s ,s ) and (s ,s ) denote the alongwith thecorrespondingclassdistancefunctions,andthe 1 2 6 ′1 ′2 1 2 ′1 ′2 complex points in , such that the distance between the class representatives. eff S two elements of a pair is same for all pairs in and this Wedefinethesetofallclassdistancefunction,d¯(γ,θ)and property holds for all values of γ and θ, though thCe value of the set of all fade state distance functionsd ( )Cas follows, Γ,Θ C the distance depends on (γ,θ). d¯(γ,θ)= d (γ,θ) ¯ Foragiveninputconstellation ,let ¯denotethesetofthe C { C |C ∈C} all distance classes for it. S C dΓ,Θ(C)={dγ,θ(C)|(γ,θ)∈(Γ,Θ)plane}. From Definition 1, at a singular fade state the value of at Definition 3: Associated with every distance class is a function d (γ,θ) : (Γ,Θ) R, called the class diCstance leastoneoftheclassdistancefunctionsind¯(γ,θ)willreduce function, wChich gives the va↔lue of the distance between the to zero. C Lemma 4: Among the set of all class distance functions two elements of a pair in for any (γ,θ). C that reduce to zero at the singular fade state (γ ,θ ), there is Definition 4: For a given fade state (γ,θ), the function ′ ′ a particular one which is the minimum amongthat set, for all d ( ) : ¯ R gives the value of the distance between thγe,θtwCo eleCme→nts of a pair in , for any ¯. This is called values of (γ,θ)6=(γ′,θ′). C C ∈C Proof: Let L be the number of class distance functions the fade state distance function. that reduce to zero at the singular fade state (γ ,θ ). Denote ′ ′ We use integer m, 1 m M to represent the point these by d (γ,θ), 1 i L and let (s ,s ),(s ,s ) emj(+m−MM1)2(πnin 1S),i.1e. thqe M≤-MPS2Kd≤esnigonteasl tsheet.cTohmepilnextegpeorinqt i=n (b3e)tahnedre(4p)rC,eisweenthataivvee≤elem≤ent for the {dist1a,nice2,cilass′1C,ii. F′2r,oim} − ≤ ≤ obtained by combining the points m and n of i.e. it rSeeffefrsto the pointej(m−M1)2π +γejθej(n−M1)2π in eff. FSor each d2Ci(γ,θ)=d2(s1,i,s2,i)↔(s′1,i,s′2,i) distanceclassC,amongallthepairs(i,j)∈C chSoosetheone =|(s1,i−s′1,i)+γejθ(s2,i−s′2,i)|2 withtheminimumvalueofi+jtobetherepresentativein .If s s C = s s 2 γejθ+ 1,i− ′1,i 2 morethanonepairhasthesame valueofi+j choosetheone | 2,i− ′2,i| | s s | withthelowestvalueofiastheclassrepresentative.Whenthe 2,i− ′2,i usersM-PSKsignalsetatinput,thereare M2(M2−1) pairwise =|s2,i−s′2,i|2|γejθ−γ′ejθ′|2. (9) 2 distancesin . Thesepairwise distancesare thuspartitioned From (9), these L class distance functions differ only in the eff S into distance classes. constant coefficient s s 2. From Definition 2, all these | 2,i− ′2,i| Example 2: Fig. 2, shows when both users use QPSK coefficients are different. Let eff S dcoisntastneclelastiaonnds2fo0rd(isγt,aθn)ce=cla(2ss,e1s4.◦T).heTsheearreealrieste1d20inpTaairbwleisIe, l′ =arg 1miinL|s2,i−s′2,i|2. ≤≤ TABLE I: Distance classes when both users use QPSK signal set. k1 C(1k,2),(1,4),(2,3),(3,4),(5,6),(6,7),(7,8),(5,8), d√C2k(γ,θ) C(1la,s2s)representative (9,10),(10,11),(11,12),(9,12),(13,14),(14,15),(15,16),(13,16) 2 (1,3),(2,4),(5,7),(6,8),(9,11),(10,12),(13,15),(14,16) 2 (1,3) 3 (1,6),(1,16),(2,15),(4,7),(6,11),(5,12),(11,16),(10,13) 2γ2+2+4γcosθ (1,6) 4 (1,8),(2,7),(2,13),(3,16),(6,9),(7,12),(11,14),(12,13) 2γ2+2+4γsinθ (1,8) 5 (1,14),(4,15),(3,6),(4,5),(8,11),(6,10),(9,16),(10,15) 2γ2+2 4γsinθ (3,6) 6 (2,5),(3,8),(3,14),(4,13),(7,10),(8,9),(12,15),(9,14) 2γ2+2−4γcosθ (2,5) 7 (1,5),(1,13),(4,8),(2,6),(2,14),(3,7),(3,15),(4,16), 2γ2 − (1,5) (6,10),(7,11),(8,12),(5,9),(12,16),(11,15),(10,14),(9,13) 8 (1,9),(2,10),(3,11),(4,12),(6,14),(5,13),(7,15),(8,16) 4γ2 (1,9) 9 (1,7),(2,16),(6,12),(11,13) 2γ2+4+4γcosθ+4γsinθ (1,7) 10 (1,15),(4,6),(5,11),(10,16) 2γ2+4+4γcosθ 4γsinθ (4,6) 11 (3,13),(2,8),(7,9),(12,14)) 2γ2+4 4γcosθ+−4γsinθ (2,8) 12 (3,5),(8,10),(9,15),(4,14) 2γ2+4−4γcosθ 4γsinθ (3,5) 13 (1,12),(2,11),(6,13),(7,16) 4γ2+2−+4γcosθ−+4γsinθ (1,12) 14 (1,10),(6,15),(4,11),(5,16) 4γ2+2+4γcosθ 4γsinθ (1,10) 15 (2,9),(3,12),(7,14),(8,13) 4γ2+2 4γcosθ+−4γsinθ (2,9) 16 (3,10),(8,15),(4,9),(5,14) 4γ2+2−4γcosθ 4γsinθ (3,10) 17 (1,11),(6,16) 4γ2+4+−8γcosθ− (1,11) 18 (2,12),(7,13) 4γ2+4+8γsinθ (2,12) 19 (3,9),(8,14) 4γ2+4 8γcosθ (3,9) 20 (4,10),(5,15) 4γ2+4−8γsinθ (4,10) − Now, from(9), d (γ,θ) is minimumamongall d (γ,θ) for Step 2 For the singular fade state (γ ,θ ) in , identify the all values of (γ,θC)l′=(γ′,θ′). Ci set of class distance function1s in1d¯(γH,θW) that reduces Definition 5: The6 regioncorrespondingto distance class , to zero at that singular fade state (Cγ ,θ ). Choose the 1 1 C ( )denotestheregioninthecomplexplane (Γ,Θ)/ for one among them, which is minimum in that set for all R C { H} whichthe classdistance functiond (γ,θ) givesthe minimum values of (γ,θ) = (γ ,θ ). (From Lemma 4, there is 1 1 distance in , i.e., C always only one6such class distance function.) Let this eff S class distance function be d (γ,θ) corresponding to R(C)={(dγ,(θγ),θ∈){(Γd,Θ()γ/,Hθ)}f|or all ′ = ¯ . dtoistoabntcaeincalasssetCokf1.cRlaespsedaitsttahCniksc1efofrunaclltio(nγsi,θdi) ∈(γH,Wθ),, C ≤ C′ C 6 C ∈C} { Cki 1 i N . Each d (γ,θ) reduces to zero at the Definition 6: When both the users use M-PSK constella- sin≤gula≤rfadWes}tate (γ ,θC)ki. Thisisthesetofallpossible tions at the input, ( ) denotes the portion of the region i i RW C class distance functions other than d ( ), that can ( ) lying in the wedge [0,π/M], i.e., min S R C possibly produce the minimum distance in eff. S ( )= ( ) wedge[0,π/M]. Step 3 To find the region ( ), we need to obtain the val- RW C R C ∩ ues of (γ,θ) weRdgWe[0C,kπi/M] for which d2 (γ,θ) Notethat,whenboththeusersuseM-PSKconstellationsat d2 (γ,θ) wh∈ere 1 j = i N , and d2Cki(γ,θ) ≤ the input, for some ¯the correspondingregion ( ) can Ckj ≤ 6 ≤ W Cki ≤ C ∈C R C d2 ( ). The curves d2 (γ,θ) = d2 (γ,θ), 1 i = civbdslaeCald(suaγse,nCθou)fl∈ld(=γosC¯ee,tdsθf,o)nbroeinwtc(ahg{uii)(svc.ΓeheW,tttΘhhheeee)d\aemasnsHsisonoot}icecm.iiatauThttemeihsddeprdcceaillsraatitssasiscsnuacddllewaiissriattnaadynnisSsccteeeaaffnffdcuufieonsnrtcccattlaniiaooncsnynes pajrenamgid≤riinowCniSkssNje.WcboTo,rhurefenosdprcamournyrdvtbhienesetgwdptCe2Coakekiiinrt(whtγhei,seeθtwr)ebog=oiuodnnidCsdsk2mtajacrinonycr(reSebsec)ptlwaofsonesrdee≤minsngCtthhkt6oeei (γ,θ) min afusnCcCdtimoinn(iSs)t.hFeruopmpSeLrebmomunad1f,orthtehevamluineimofumthisdicstlaansscediisntance. disisttahnactercelgaisosnesiCnkithaendwCeddmgien(S[0),.πT/hMe r]egeixocnluRdiWng(Ctkhie) eff For example when both users use QPSK signal sets atSthe complex point (γi,θi), which is the innermost region input, then from Table I, = and the associated boundedbythesepairwiseboundaries,enclosingthesin- class distance function is dCCd1m(γin,(θS))=dCm1in(S)=√2. rgeugliaornfacdoerrsetsapteon(dγiin,gθit)o. Fthoerseixnagmulpalre,faFdige.s6tadteepaitc(ts1,th0e) Theproceduretoobtainthequantizationofthe(Γ,Θ)plane, when both users use 8-PSK signal sets. In the figure, when both users use M-PSK constellations at the input, is as the curve d2 = d2 refers to the curve d2 (γ,θ) = follows: 1 j Ck1 d2 (γ,θ), and d2 = 2 √2 refers to the curve Step 1 Othbetawinedtghee[N0,Wπ/sMing].uElaarchfadoef tshtaetseessiinngHulWarif.aed.,elystiantgeiins dC2kk(γ,θ)=2 √12. It is th−e innermostregion (shaded denoted by (γ ,θ ) where 1 i N . inCkt1hefigure)in−thewedge[0,π/8]boundedbythepair- i i W ≤ ≤ Fig. 3: Quantization of the wedge [0,π/4] for QPSK signal Fig.4:Quantizationoftheentire(Γ,Θ)planeforQPSKsignal sets. sets wise boundaries d2 (γ,θ) = d2 (γ,θ), d2 (γ,θ) = the quantization obtained for θ [0,π/4] is reflected along d2 (γ,θ), d2 (γ,Cθk1) = d2 (γC,kθ2) and d2Ck1(γ,θ) = the line θ = π/4 to obtain the∈quantization for the wedge d2Ck4(γ,θ) suCrkr1ounding theCks5ingular fade Cskta1te (1,0). [0,π/2]. This is now rotated by kπ, 1 k 3, to obtain the OCnkc6e the regions ( ), 1 i N are obtained, quantization for θ kπ,(k+1)π2 , th≤us co≤vering the entire R Cki ≤ ≤ W ∈ 2 2 the region exterior to all these regions, lying within the (Γ,Θ) plane. This hashbeen showniin Fig. 4. wedge [0,π/M], is the region where d ( ) is the min Example 4: Channel quantization for 8-PSK signal sets S minimumdistancein ,i.e.,theregion ( ). Step 4 The quantization obtSaeifnfed in Step 3, RfoWr tChdemwine(Sd)ge Here we consider the scenario when both users use 8-PSK signal sets at the input. The number of singular fade states [0,π/M], can now be extended by the procedure sug- lying in the wedge [0,π/8] is, N = 7. The singular fade W gested in Section II-A to cover the entire (Γ,Θ) plane. states (γ ,θ ), 1 i 7 are as follows: i i We will illustrate the procedure with two examples. ≤ ≤ (1,0), (√2,0), (1+√2,0), Example 3: Channel Quantization for QPSK signal sets. Here we consider the scenario where both users use QPSK π 1 π constellations at input, i.e. M =4. From Lemma 3, there are 4 2√2, , 1+ , , twosingularfadestatesinthewedge[0,π/4],i.e.N =2and (cid:18)q − 8(cid:19) s √2 8! W these are at (1,0) and (√2,π4). The class distance functions 2+√2,π , 4+2√2,π . in d¯(γ,θ) which reduce to zero at these singular fade states (cid:18)q 8(cid:19) (cid:18)q 8(cid:19) are iCdentified.For the singularfade state (√2,π) the distance 4 The class distance functionsin d¯(γ,θ) which reduce to zero bdoCkth1 ffaallllstotozezreoro,,asansdhofworn(i1n,0F)igth2e. TdihsetasnecaersedaCsk2foallnodwsd:Ck3 foreachofthe abovesingularfadCestatesareidentified.When more than one class distance function reduces to zero at a d2 (γ,θ)=2γ2+4 4γcosθ 4γsinθ singular fade state (γi,θi), the one which is minimum among Ck1 − − them for any other (γ,θ) = (γ ,θ ) is chosen. The class d2 (γ,θ)=2γ2+2 4γcosθ 6 i i d2Ck2(γ,θ)=4γ2+4−8γcosθ =2d2 d2 . dshisotwannceinfuFnigc.tio5n.sIndCtkhie(γfi,gθu)r,e1d≤deino≤tes7thaerecliadsesntdifiisetadncaes i Ck3 − Ck2 ≥ Ck2 function d (γ,θ). These are as follows As d (γ,θ) > d (γ,θ) for all values of (γ,θ) = (1,0), Cki we coCkn3sider the claCsk2s distance function correspondin6 g to the d2 (γ,θ)=(2 √2)(γ2 2γcosθ+1) osibntgauinlarthfeadreegsiotantse (1,0() as),dCk2(γ(,θ)). Nanodw we(proceed t)o. dC2k1(γ,θ)=2γ2−+4 4√−2γcosθ The pair-wise boundRaWriesCka1re oRbtWainCedk2as folloRwWs, Cdmin(S) d2Ck2(γ,θ)=(2 √2)−γ2+2+√2 2√2γcosθ Ck3 − − d2 (γ,θ)=(2+√2)γ2+4 2(2+√2)γcosθ 2√2γsinθ d2 (γ,θ)=d2 (γ,θ) γsinθ=1/2 Ck4 − − Ck1 Ck2 ⇒ d2 (γ,θ)=2γ2+2+√2 2(1+√2)γcosθ 2γsinθ d2Ck1(γ,θ)=d2min(S)=2⇒(γcosθ−1)2+(γsinθ−1)2=1 d2Ck5(γ,θ)=(2 √2)γ2+−2 2(√2 1)γsinθ− 2γcosθ d2Ck2(γ,θ)=d2min(S)=2⇒(γcosθ−1)2+γ2sin2θ=1. d2Ck6(γ,θ)=(2−√2)γ2+4−2(2 −√2)γsinθ−2√2γcosθ. TheseregionsareshowninFig.3forthewedge[0,π/4].This Ck7 − − − − can now be extended to cover the entire range of θ. For this, Now to obtain the region ( ) we need to obtain the RW Ck1 A. Adaptive Modulation Scheme It is clear from Section II-B that the minimum distance in falls to zero at the singular fade states. For fade eff S states (γ,θ) lying close to a singular fade state, the minimum distance in is very low, resulting in degradation of error eff S performance at the destination. Hence, such values of (γ,θ) have to be avoided to provide better performance. Our goal is to provide a minimum distance guarantee of δ in i.e., not allow minimum distance in to fall eff eff S S below δ. In the previous subsection, the regions ( ) on R Cki the (Γ,Θ) plane was identified, in which the class distance functiond (γ,θ), 1 i N givesthe minimumdistance Cki ≤ ≤ W in . In order to satisfy the minimum distance guarantee of eff S δ in , it is thus required to avoid the fade states (γ,θ) for eff S which d (γ,θ)<δ, 1 i N . Fig.5:Effectiveconstellation for(γ,θ)=(2.9,10 )when AttheCskiingularfadesta≤te(γ≤,θW),theclassdistancefunction eff ◦ i i S both users use 8-PSK signal set. d (γ,θ) reduces to zero. If (s ,s ),(s ,s ) is the reCpkriesentative element for the{di1s,tianc2e,i clas′1s,i ′2,i, }then at Cki the singular fade state (γ ,θ ) the two points (s ,s ) and i i 1,i 2,i curves d2 (γ,θ) = d2 (γ,θ), 2 j 7 and d2 (γ,θ) = (s ,s )collapsetoasinglepointin .Fromthedefinition Ck1 Ckj ≤ ≤ Ck1 ′1,i ′2,i Seff d2 ( )=2 √2. These are as follows: of singular fade state (4), we have min S − s s d2Ck1(γ,θ)=d2Ck2(γ,θ)⇒(γcosθ−(3−1 √2))2+γ2sin2θ=10−7√2 γiejθi =−s12,,ii−−s′1′2,,ii. d2 (γ,θ)=d2 (γ,θ) γcosθ= Ck1 Ck3 ⇒ 2 √2 From (3), we have − 1 3 2√2 d2Ck1(γ,θ)=d2Ck4(γ,θ)⇒(γcosθ−1)2+1(γsinθ− 2)2= 1−4 dCki(γ,θ)=|s2,i−s′2,i||γejθ −γiejθi|. (10) d2Ck1(γ,θ)=d2Ck5(γ,θ)⇒(γcosθ−2+ √2)2+(γs=in3θ−2√√22)2 1OnlyithosNeWfadheavsetattoesb(eγa,vθo)idwehdi,chi.er.e,sfurlotsmin(1d0C),kiw(γe,nθe)e<d tδo, − ≤ ≤ 1 avoid the fade states (γ,θ), for 1 i N , where d2 (γ,θ)=d2 (γ,θ) γcosθ+γsinθ=1+ ≤ ≤ W Ck1 Ck6 ⇒ √2 δ d2 (γ,θ)=d2 (γ,θ) √2γcosθ+γsinθ= 3 +√2 γejθ γiejθi < . (11) dC2k1(γ,θ)=2Ck7√2 (⇒γcosθ 1)2+γ2sin2θ2=1. | − | |s2,i−s′2,i| Ck1 − ⇒ − Theaboveequationrepresentsacircularregioninthecomplex plane (Γ,Θ) centred at the singular fade state (γ ,θ ) and i i All of the above curves are shown in Fig. 6. In the figure, radius δ/s s . We call these circular regions, the the curved2 =d2 refersto the curved2 (γ,θ)=d2 (γ,θ), | 2,i − ′2,i| 1 j Ck1 Ckk violation circles because when the fade state lies inside them andd2 =2 √2referstothecurved2 (γ,θ)=2 √2.The theminimumdistancerequirementof isviolated.Forfade region1 (− )istheinnermostregiCokn1inthewed−ge[0,π/8] states outside the violation circles thSeefmf inimum distance in RW Ck1 boundedbythesecurves,surroundingthepoint(1,0).Itisthe isalwaysgreaterthanδ. Theradiusoftheviolationcircle eff S shadedregionintheFig.6.Alltheregions ( ),1 i centred at the singular fade state (γ ,θ ) by is denoted by RW Cki ≤ ≤ i i 7 can be obtained by the same procedure.The regionexterior ρ(γ ,θ ). Formally violation circles are defined as follows: i i to all these regions, inside the wedge [0,π/8] is the region Definition 7: Violation Circles are circular regions on the RwdiesWdtag(nCecde[m0iin,nπ(SS/e)8f)f].,Tiwshhuoesbr,teathidnemeqdiun.a(InStt)iizs=astihpoonw2on−ftihs√eF2fiagids.et7hsteiantmetsihnfeiomrnutehxmet N(−Γss,21Θ,,.ii−−)ssp′2′1l,,aiinweiwthitrhadceiunstrρes(γait,tθhie)s=inδg/u|lsa2r,ifa−des′2s,tia|tefsor(γ1i,≤θi)i ≤= page. This can now be extended to cover the entire (Γ,Θ) W It is observed that the the violation circles centred at plane by the similar technique used for the QPSK case in the (γ ,θ +p2π),1 i N and1 p M 1havethesame Example 3. i i M ≤ ≤ W ≤ ≤ − radius as the one centred at (γ ,θ ), where (γ ,θ ) . i i i i W III. THE ADAPTIVEMODULATION SCHEME This is because from Lemma 2, the corresponding e∈ffeHctive In this section the fade states which results in reducing the constellations are the same. minimumdistancein belowaminimumdistanceguarantee Example 5: When both users use QPSK constellations at eff S of δ are identified.Then a modulationschemeis proposedfor the input,the violationcircles areas follows.At singularfade theuserstoavoidthesefadestatesbysuitablerelativerotation state (√2,π/4) the class distance function d (γ,θ) reduces Ck1 between the signal sets used by the two users. tozero,i.e.thepoints3and5in collapsetoasinglepoint, eff S Fig. 6: The figure explains how to region (d ) (shaded region in the figure) corresponding to the singular fade state (1,0 ) 1 ◦ R is obtained. Fig. 7: Channel quantization for θ [0,π/8] when both users use 8-PSK signal sets ∈ as shown in Fig. 2. The 3 and 5 are obtained after combining in Table II. 3, 1 and 1, 2 respectively. Thus, s s =√2. ∈S ∈S | 2,1− ′2,1| When the fade state (γ,θ) lies inside any of the violation The violation circle corresponding to class distance function circles the users need to adapt their transmission, in order d (γ,θ) is the circular region centred at (√2,π/4) and Ck1 to avoid these fade states effectively. One way to achieve radius δ/√2. Similarly, for the singular fade state at (1,0) this without increasing the transmit power, is to rotate the the violationcircle hasa radiusof δ/√2. These are shownby constellation of User-2. Rotation can be interpreted as simply dotted circles around the singular fade states in Fig. 4. altering the phase of the fade state. Example 6: When both users are using 8-PSK constella- Lemma 5: When the fade state is (γ,θ), rotation of the tions at the input, the centresand radiiof the violationcircles constellation of User-2 by an angle α with respect to the corresponding to the distances d , 1 i 7 are tabulated constellation of User-1 in an anticlockwise direction, results Cki ≤ ≤ TABLE II: Centre and Radius of violation circles for 8-PSK the wedge [0,π/M]. In order to obtain the optimal angle of case rotationfortheviolationcirclecentredat(γ ,θ ),itisrequired i i i Centre Radius to calculate for fixed γ = γi the value of phase θ = θi,opt, 1 (1,0) δ θ [0,π/M] which maximizes the minimum distance in √2 √2 ∈ 2 (√2,0) −δ eff. Thus after rotation the violation circle centred (γi,θi) 3 (√2+1,0) √δ2 Sis shifted such that its new centre is the point (γi,θi,opt) on √2 √2 the(Γ,Θ)plane.Werefertothisrotatedviolationcircleasthe − 4 (cid:16)p4−2√2,π8(cid:17) √2+δ√2 effective shifted circle. We now prove two lemmas to obtain 56 (cid:16)(cid:16)qp12++√√122,,π8π8(cid:17)(cid:17) √2√−δδ2√2 wthheLicevhmalrmueeaduθ6ci:,eospLtteowtzhederCnokiab(toγtt,hhθe)ussiebnregsuutlhasreefMacdlae-sPssStaKdteiss(tiaγgnin,caθeli)sfeutns.ctiWon. 7 (cid:16)p4+2√2,π8(cid:17) √2−δ√2 For a fixed γ0 and (γ0,θ) lying within the wedge [0,∈π/HM], the value of d (γ ,θ) increases as the difference θ θ Cki 0 | i − | increases. in effectively altering the phase of the fade state from θ to Proof: From (10), we have θ+αP.roof: Let be the constellation being used by both the d2Cki(γ0,θ)=|s2,i−s′2,i|2|γ0ejθ−γiejθi|2 users at the inpuSt. Now the User-2 rotates its constellation by =|s2,i−s′2,i|2γ02|1−γ′ej(θi−θ)|2whereγ′ =γi/γ0 >0 angle α in the anticlockwise direction, such that it can now =|s2,i−s′2,i|2γ02n1+γ′2−2γ′cos|θi−θ|o. berepresentedasejα .Theeffectiveconstellation canbe eff S S As cosφ is a decreasing function of φ, 0 φ π/M, written as ≤ ≤ d2 (γ ,θ) increases as θ θ increases. This proves the 0 i +γejθ ejα = +γej(θ+α) . leCmkima. | − | S { S} S S Lemma 7: Let (γ ,θ ) be a singular fade state. Let Hence, the fade state (γ,θ) is transformed to (γ,θ+α) after i i ( ) and ( ) be the regions surrounding the sin- rotation. RW Cka RW Ckb gular fade states (γ ,θ ) and (γ ,θ ) respectively. Consider The proposed strategy is thus, to rotate the signal set of a a b b the arc traced by the point (γ ,θ) that lies within the wedge User-2 whenever the fade state (γ,θ) lies within any of the i [0,π/M] as θ varies in the direction to move away from violation circles such that the transformed fade state lies the singular fade state (γ ,θ ). Let the region ( ) is outside the violation circles, in order to satisfy the minimum i i R Cka encounteredbefore ( )asθvaries.Wehavethefollowing: distanceguaranteein eff.Forfadestatesoutsidetheviolation R Ckb S (i) The minimum distance in is maximized at one of circles no rotation is required. The destination which has eff S the points of intersection of this arc and the boundaries complete CSI sends feedback of log (N +1) bits to the usersto indicate in whichone oft⌈he v2iolaWtioncirc⌉lesthe fade between the regions R(Cka) and R(Ckb). (ii) Amongallthepointsin(i),thosethatlieontheboundary state lies, or if it lies outside all of them. between ( )and ( )withθ =θ =θ cannever R Cka R Ckb i a b B. Optimal Angle of Rotation for the M-PSK case correspond to the maximum value. Definition 8: An optimal rotation angle, for a violation Proof: The proof for part (i) is as follows. Let A and B circle with centre at singular fade state (γ ,θ ) , 1 i N bethefirstandthesecondpointsofintersectionofthearcwith i i W ≤ ≤ is that angle of rotation which maximizes the minimum the boundary of the region ( ). From Section II-B, the RW Cka distance in for the same transmit power, when fade state valueofclassdistancefunctiond (γ,θ)givestheminimum (γ,θ)=(γS,θeff). distance in when (γ,θ) Cka ( ). Now if θ = θ , i i Seff ∈ RW Cka a i It should be noted for non-singular fade states inside the then from Lemma 6, d (γ ,θ) increases as (γ ,θ) moves violation circle, the minimum distance in after rotation from A to B. Likewise,Ckiaf θi = θ , then again froim Lemma eff a i willbelessthanwhatitcouldhavebeenifthSefadestate(γ,θ) 6, d (γ ,θ) decreasesas one6movesfromA to B. Thusthe wasexactlyknownatthe users. Whenbothusersuse M-PSK miniCmkaumidistance in can never be maximum for (γ ,θ) eff i S constellations at the input, it is sufficient to concentrate on lying inside the regions ( ). It can only be maximized RW Cka the violation circles centred at (γ ,θ ) , because the at the points of intersection of the arc with the boundary of i i W ∈ H optimal rotation angles for these, is also optimal for other the region. such circles centred at (γ ,θ +p2π), where 1 p M 1. To prove the second part of the lemma, we assume θ = i i M ≤ ≤ − i This follows from the fact that the corresponding effective π/M. Consider the scenario shown in Fig. 8. To prove part constellations are equivalent. (ii), we need to show that the minimum distance in can eff From Lemma 5, rotation of the constellation of User-2 never be maximum at the point B. In the region S ( ) RW Cka relativetoUser-1,resultsineffectivelyalteringthephaseofthe the value of class distance function d (γ,θ) gives the fade state. Rotation thus results in movingthe violation circle minimum distance in . As (γ ,θ) moCvkaes from A to B, eff i S with centre at singular fade state (γ ,θ ), along a circular arc from Lemma 6, the minimum distance in , i.e. the value i i eff such that its centre always lie on the curve γ =γ and within of d (γ ,θ), increases since θ θ incSreases. At B, we i Cka i | a − | Fig. 8: Diagram illustrates the variation of the minimum distance in , for fixed γ on varying θ eff i S have d (γ ,θ) = d (γ ,θ). Beyond B, in the region Fig. 9: Optimal rotation angles for the QPSK case Cka i Ckb i ( ), the class distance function d (γ,θ) gives the mRiWnimCukbm distance in . As (γ ,θ) moCvkebs from B to C, eff i S If θ = π/M, from Lemma 5, the optimal rotation is θb θ increases,thus fromLemma6, the minimumdistance • i i|cnanS−nefef,v|ie.re.ctohrerevsaplounedotfodtChkeb(pγoii,nθt)wchoenrteinthueesmtoiniinmcuremasdei.sStaoncBe αIfi,θoipt==0,πf/rMom−Lθeim,omptain5,athceloocpktwimisaelrdoirtaetcitoionni.s αi,opt = • θ in an anticlockwise direction. in is maximized. The proof for the case when θ = 0 is i,opt eff i exaSctly similar to the above proof. This completes the proof. Example 7: Optimal angles for QPSK signal sets When both users use QPSK constellations at input, the channel Theproceduretoobtaintheoptimalphaseθ ofthefade quantization is shown in Fig. 3. The optimal rotation angle i,opt state, for the violation circle centred at singular fade state are calculated as shown below. These are shown in Fig. 9. (γ ,θ ) is stated as follows: Forviolationcirclecentredat(√2,π),theoptimalphase i i ∈HW • 4 Step 1 Find the points of intersections of the arc γ = γi, θ θ1,opt is the phase of pointof intersectionof the arc γ = [0,π/M], with the boundaries that satisfy the condition∈s √2 and pairwise boundary d2 (γ,θ) = d2 (γ,θ) i.e. mentioned in Lemma 7. γsinθ = 0.5. Therefore, θ1,opCtk1= sin−1(2√1C2k2) ≈ 20.7◦. Step 2 Ifthereisonlyonesuchpointofintersection,saywiththe Thus the optimal rotation angle for the constellation of boundary between the regions ( ) and ( ), User-2relativetoUser-1isα =45 20.7 =24.3 RW Cka RW Ckb 1,opt ◦− ◦ ◦ θ is obtained by solving the equation d2 (γ,θ) = in a clockwise direction. i,opt d2 (γ,θ) . On the other hand, if thereCakrae L such For violation circle centred at (1,0), the optimal phase poCkinbts of|γin=tγeirsections, say with boundaries between • corresponds to the point of intersection of the arc γ =1 regions ( ) and ( ), 1 l L, calculate and boundary d2 (γ,θ)=d2 (γ,θ), i.e. γsinθ =0.5. thephasReoWfeCakcah,lofthesRepWoinCtksb,olfinte≤rsec≤tion,θl,intersect, Thus θ2,opt = siCnk1−1(0.5) = 3C0k2◦. Thus the optimal rota- 1 l L by solving the equation d2 (γ,θ) = tion anglefor User-2 is α =30 in an anticlockwise d2≤ (γ,≤θ) . Then compute the minimCukma,ldistances direction relative to User-21,.opt ◦ inCkb,l for|γt=heγi fade state corresponding to the point Example 8: Optimal Angles for 8-PSK signal sets When eff S of intersection (γ ,θ ) as d (γ ,θ ) = both users are using 8-PSK constellations at the input, the i l,intersect min i l,intersect d2 (γ,θ) . Choose channel quantization is obtained as shown in Fig. 7. The Cka,l |γ=γi,θ=θl,intersect optimalanglesofrotationfor User-2relative to User-1,α i,opt l′ =arg max dmin(γi,θl,intersect). canbecalculatedusingthesametechniqueforalltheviolation 1 l L ≤≤ circles centred at the singular fade states (γ ,θ ), 1 i 7. i i Then we have, For each (γ ,θ ), 1 i 7, the boundaries corres≤pon≤ding i i ≤ ≤ to the optimal phase, θ and α are tabulated in Table θ =θ . i,opt i,opt i,opt l′,intersect III. The letters (C) or (A) in the column corresponding to The optimal rotation angles for the violation circle with α indicates the direction of rotation as clockwise and i,opt centres at (γi,θi), can now be easily calculated from θi,opt. anticlockwise respectively. The optimal rotation angle, α , for the violation circle i,opt centred at (γ ,θ ) is that rotation angle that transforms the C. Upper Bound on δ i i fade state from (γ ,θ ) to (γ ,θ ). (See Lemma 5.) Inthissubsectionweobtainanupperboundonδ forwhich i i i i,opt For violation circles with centre at (γ ,θ ) , 1 i N , theproposedrotationschemecanbeemployed.Itisnecessary i i W ≤ ≤ the optimal rotation angles for the User-2 are as follows: that the violation circle corresponding to any of the singular
The list of books you might like

Rich Dad Poor Dad

As Good as Dead

Corrupt (Devil's Night #1)

The Silent Patient
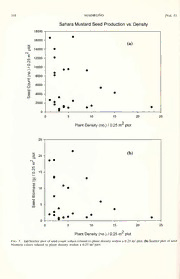
SEED PRODUCTION BY THE NON-NATIVE BRASSICA TOURNEFORTII (SAHARA MUSTARD) ALONG DESERT ROADSIDES

Investigating Psychology 2 - From Social to Cognitive

Carleson Potentials and the Reproducing Kernel Thesis for Embedding Theorems

Haryana Gazette, 2006-01-04, No. 4

NEW SPECIES AND RECORDS OF THE PSEUDOSCORPION FAMILY MENTHIDAE (PSEUDOSCORPIONES)

China and the Middle East: from Silk Road to Arab Spring

Meet the Masters

Economics: A Primer for India

Greek Government Gazette: Part 4, 2006 no. 465

Project 1 - Workbook (3rd Edition)

DTIC ADA275521: CBSD: The Celestial Background Scene Descriptor

Un canalla que no lo era

Yoga Cures: Simple Routines to Conquer More Than 50 Common Ailments and Live Pain-Free

EatingWell soups: 100 healthy recipes for the ultimate comfort food

C anton €>0sctt»er

Advancements in Genetic Linkage Maps and Quantitative Trait Locations of Aquatic Farming Animals




