
Quantum Walks and Search Algorithms PDF
Preview Quantum Walks and Search Algorithms
Quantum Science and Technology Renato Portugal Quantum Walks and Search Algorithms Second Edition Quantum Science and Technology Series editors Raymond Laflamme, Waterloo, Canada Gaby Lenhart, Sophia Antipolis, France Daniel Lidar, Los Angeles, USA Arno Rauschenbeutel, Vienna, Austria Renato Renner, Zürich, Switzerland Maximilian Schlosshauer, Portland, USA Yaakov S. Weinstein, Princeton, USA H. M. Wiseman, Brisbane, Australia Aims and Scope The book series Quantum Science and Technology is dedicated to one of today’s mostactiveandrapidlyexpandingfieldsofresearchanddevelopment.Inparticular, the series will be a showcase for the growing number of experimental implemen- tations and practical applications of quantum systems. These will include, but are not restricted to: quantum information processing, quantum computing, and quantum simulation; quantum communication and quantum cryptography; entan- glement and other quantum resources; quantum interfaces and hybrid quantum systems; quantum memories and quantum repeaters; measurement-based quantum control and quantum feedback; quantum nanomechanics, quantum optomechanics and quantum transducers; quantum sensing and quantum metrology; as well as quantum effects in biology. Last but not least, the series will include books on the theoretical and mathematical questions relevant to designing and understanding these systems and devices, as well as foundational issues concerning the quantum phenomena themselves. Written and edited by leading experts, the treatments will be designed for graduate students and other researchers already working in, or intending to enter the field of quantum science and technology. More information about this series at http://www.springer.com/series/10039 Renato Portugal Quantum Walks and Search Algorithms Second Edition 123 RenatoPortugal National Laboratory of Scientific Computing(LNCC) Petrópolis, Brazil ISSN 2364-9054 ISSN 2364-9062 (electronic) QuantumScience andTechnology ISBN978-3-319-97812-3 ISBN978-3-319-97813-0 (eBook) https://doi.org/10.1007/978-3-319-97813-0 LibraryofCongressControlNumber:2018950813 1stedition:©SpringerScience+BusinessMediaNewYork2013 2ndedition:©SpringerNatureSwitzerlandAG2018 Thisworkissubjecttocopyright.AllrightsarereservedbythePublisher,whetherthewholeorpart of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission orinformationstorageandretrieval,electronicadaptation,computersoftware,orbysimilarordissimilar methodologynowknownorhereafterdeveloped. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publicationdoesnotimply,evenintheabsenceofaspecificstatement,thatsuchnamesareexemptfrom therelevantprotectivelawsandregulationsandthereforefreeforgeneraluse. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authorsortheeditorsgiveawarranty,expressorimplied,withrespecttothematerialcontainedhereinor for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictionalclaimsinpublishedmapsandinstitutionalaffiliations. ThisSpringerimprintispublishedbytheregisteredcompanySpringerNatureSwitzerlandAG Theregisteredcompanyaddressis:Gewerbestrasse11,6330Cham,Switzerland To my father (in memoriam) Preface This is a textbook about quantum walks and quantum search algorithms. The readers will take advantage of the pedagogical aspects and learn the topics faster andmakelesseffortthanreadingtheoriginalresearchpapers,oftentooconvoluted. The exercises and references allow the readers to deepen their knowledge on specific issues. Guidelines to use or to develop computer programs for simulating the evolution of quantum walks are also available. Almostnothingcanbeextractedfromthisbookifthereaderisunfamiliarwiththe postulatesofquantummechanics,describedinthesecondchapter,andthematerial on linear algebra described in Appendix A. Some extra bases are required: It is desirablethatthereaderhas(1)notionsofquantumcomputing,includingthecircuit model, references of which are provided at the end of Appendix A, (2) notions of graph theory, references of which are provided at the end of Appendix B, and (3) notions of classical algorithms and computational complexity. Any undergrad- uate or graduate student with this background can read this book. Some topics addressed in this second edition are currently active research areas with impact on thedevelopmentofnewquantumalgorithms.Becauseofthat,researchersworking with quantumcomputing may findthis bookuseful. Thesecondeditionbringsatleastthreemainnovelties:(1)anewchapteronthe staggered quantum walk model—Chap. 8, (2) a new chapter on the element dis- tinctnessproblem—Chap.10,and(3)anewappendixongraphtheory—Appendix B. Besides, the chapter on quantum-walk-based search algorithm—Chap. 9—was rewritten,thepresentationhasbeensimplified,andnewmaterialhasbeenincluded. Corrections,suggestions,andcommentsarewelcome,whichcanbesentthrough Web page (qubit.lncc.br)or directly tothe author by email (portugal@lncc.br). Petrópolis, RJ, Brazil Renato Portugal vii Acknowledgements I am grateful to many people, including colleagues, graduate students, and the group of quantum computing of LNCC, friends and coauthors in research papers, projects, and conference organization. I am also grateful to many researchers for exchanging ideas in conferences and in collaborations. Some of them helped by reviewing, giving essential suggestions, and spending time on this project, in special,Drs.StefanBoettcher,NorioKonno,RaquelineSantos,andEtsuoSegawa. In January and February 2018, I gave a short course on quantum-walk-based search algorithms at the Tohoku University under the invitation of Dr. Etsuo Segawa. I thank the students and researchers that attended the course, who raised interesting discussion topics, helping to improve some chapters of the new edition of this book. IthankTomSpicerandCindyZitterfromSpringerforencouragingmetowrite thesecondedition,whichturnedouttobeanopportunityforfixingmanyproblems ofthefirstedition andimprovingthebookbyaddingnewmaterial. Ihopetohave introduced fewer problems this time. IthankthesupportoftheNationalLaboratoryofScientificComputing(LNCC), the funding agencies CNPq, CAPES, and FAPERJ, and the scientific societies SBMAC and SBC. Last but not least, from the bottom of my heart, I thank my family, wife and sons, for giving support and amplifying my inner motivation. ix Contents 1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 2 The Postulates of Quantum Mechanics . . . . . . . . . . . . . . . . . . . . . . 5 2.1 State Space. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.1.1 State Space Postulate . . . . . . . . . . . . . . . . . . . . . . . . . 7 2.2 Unitary Evolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 2.2.1 Evolution Postulate. . . . . . . . . . . . . . . . . . . . . . . . . . . 8 2.3 Composite Systems. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2.4 Measurement Process . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.4.1 Measurement Postulate . . . . . . . . . . . . . . . . . . . . . . . . 12 2.4.2 Measurement in the Computational Basis. . . . . . . . . . . 14 2.4.3 Partial Measurement in the Computational Basis . . . . . 16 3 Introduction to Quantum Walks. . . . . . . . . . . . . . . . . . . . . . . . . . . 19 3.1 Classical Random Walk on the Line . . . . . . . . . . . . . . . . . . . . 19 3.2 Classical Discrete-Time Markov Chains. . . . . . . . . . . . . . . . . . 23 3.3 Coined Quantum Walks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 3.3.1 Coined Walk on the Line . . . . . . . . . . . . . . . . . . . . . . 26 3.4 Classical Continuous-Time Markov Chains . . . . . . . . . . . . . . . 33 3.5 Continuous-Time Quantum Walks . . . . . . . . . . . . . . . . . . . . . . 35 3.5.1 Continuous-Time Walk on the Line. . . . . . . . . . . . . . . 35 3.5.2 Why Must Time be Continuous?. . . . . . . . . . . . . . . . . 38 4 Grover’s Algorithm and Its Generalization. . . . . . . . . . . . . . . . . . . 41 4.1 Grover’s Algorithm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 4.2 Quantum Circuit of Grover’s Algorithm. . . . . . . . . . . . . . . . . . 44 4.3 Analysis of the Algorithm Using Reflection Operators . . . . . . . 45 4.4 Analysis Using the Two-Dimensional Real Space. . . . . . . . . . . 50 4.5 Analysis Using the Spectral Decomposition . . . . . . . . . . . . . . . 52 4.6 Optimality of Grover’s Algorithm . . . . . . . . . . . . . . . . . . . . . . 53 4.7 Search with Repeated Elements . . . . . . . . . . . . . . . . . . . . . . . . 59 xi xii Contents 4.7.1 Analysis Using Reflection Operators . . . . . . . . . . . . . . 60 4.7.2 Analysis Using the Reduced Space . . . . . . . . . . . . . . . 62 4.8 Amplitude Amplification. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 4.8.1 The Technique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 5 Coined Walks on Infinite Lattices. . . . . . . . . . . . . . . . . . . . . . . . . . 69 5.1 Hadamard Walk on the Line . . . . . . . . . . . . . . . . . . . . . . . . . . 69 5.1.1 Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 5.1.2 Analytic Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75 5.1.3 Other Coins . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 5.2 Two-Dimensional Lattice . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 5.2.1 The Hadamard Coin. . . . . . . . . . . . . . . . . . . . . . . . . . 81 5.2.2 The Fourier Coin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 5.2.3 The Grover Coin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 5.2.4 Standard Deviation. . . . . . . . . . . . . . . . . . . . . . . . . . . 84 5.3 Quantum Walk Packages. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 6 Coined Walks with Cyclic Boundary Conditions . . . . . . . . . . . . . . 89 6.1 Cycles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 6.1.1 Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . 91 6.1.2 Analytic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 6.1.3 Periodic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . 97 6.2 Finite Two-Dimensional Lattices . . . . . . . . . . . . . . . . . . . . . . . 98 6.2.1 Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 6.2.2 Analytic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . 104 6.3 Hypercubes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 6.3.1 Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 6.3.2 Analytic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . 114 6.3.3 Reducing a Hypercube to a Line Segment . . . . . . . . . . 115 7 Coined Quantum Walks on Graphs . . . . . . . . . . . . . . . . . . . . . . . . 125 7.1 Quantum Walks on Class-1 Regular Graphs. . . . . . . . . . . . . . . 126 7.2 Coined Quantum Walks on Arbitrary Graphs . . . . . . . . . . . . . . 127 7.2.1 Locality. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129 7.2.2 Grover Quantum Walk . . . . . . . . . . . . . . . . . . . . . . . . 130 7.2.3 Coined Walks on Cayley Graphs. . . . . . . . . . . . . . . . . 131 7.2.4 Coined Walks on Multigraphs. . . . . . . . . . . . . . . . . . . 132 7.3 Dynamics and Quasi-periodicity . . . . . . . . . . . . . . . . . . . . . . . 132 7.4 Perfect State Transfer and Fractional Revival . . . . . . . . . . . . . . 137 7.5 Limiting Probability Distribution . . . . . . . . . . . . . . . . . . . . . . . 139 7.5.1 Limiting Distribution Using the Fourier Basis . . . . . . . 142 7.5.2 Limiting Distribution of QWs on Cycles . . . . . . . . . . . 143 7.5.3 Limiting Distribution of QWs on Hypercubes . . . . . . . 147 7.5.4 Limiting Distribution of QWs on Finite Lattices. . . . . . 150
Description:The list of books you might like

Mind Management, Not Time Management

The Spanish Love Deception

Better Than the Movies

The 48 Laws of Power

Выступления полномочного представителя Президента РФ в Конституционном Суде Российской Федерации. 2015–2018 годы. Сборник. Том 2. 2017–2018 годы

Oxford Reviews of Reproductive Biology 1993: Vol 15 Index

The Hunter Cats of Connorloa by Helen Jackson H H

Greek Government Gazette: Part 2, 1993 no. 453

ERIC ED375369: Simulating Society: An Experimental Approach to Teaching Race/Class Relations.

A new stegelytrine leafhopper genus from China and Thailand (Hemiptera: Cicadellidae)

Mind Hack: A Cyberpunk Saga (Book 4)

Planet.Mars.-.Story.of.Another.World

By Blood Alone

Business and Society 2006: Vol 45 Index

Cairo University Repository
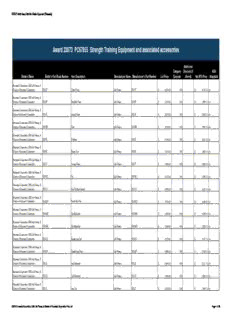
Award 23073 PC67855 Strength Training Equipment and associated accessories

The Spy Condensed for Use in Schools by J Fenimore Cooper

Guardians of Time






