Introduction to Confidence Intervals and Limit Setting via APEX - Hall A

24 Pages·2010·1.78 MB·English

Introduction to Confidence Center for
Cosmology and
Particle Physics
Intervals and Limit Setting
via APEX
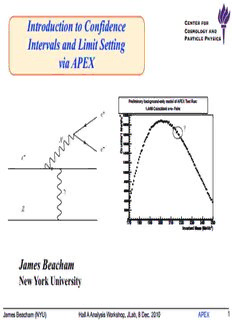
Preliminary background-only model of APEX Test Run:
TTooyy MMooddeell ooff AAPPEEXX TTeesstt RRuunn:: 11..4444MM CCooiinncciiddeenntt ee++ee-- PPaaiirrss
1.44M Coincident e+e- Pairs
e+
22 2222000000
cc
VV//
ee2200000000 ?
MM
11 1188000000
A ss//
" nntt1166000000
e uu
− oo
CC1144000000
e
−
1122000000
1100000000
88000000
γ
66000000
44000000
Z
22000000
00
117700 118800 119900 220000 221100 222200 223300 224400 225500
IInnvvaarriiaanntt MMaassss ((MMeeVV//cc22))
James Beacham
New York University
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 1
Outline Center for
Cosmology and
Particle Physics
1) Goals of statistical analysis in collider physics
Statistical inference
‣
2) Hypothesis testing
3) APEX as an example
Probability model and likelihood function
‣
Profile likelihood ratio
‣
Confidence interval from hypothesis test
‣
Look elsewhere effect
‣
Limit setting, with preliminary expected projected results
‣
4) Other methods
5) Summary
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 2
Goals of Statistical Analysis in Collider Physics Center for
Cosmology and
Particle Physics
We performed an experiment and we made some measurements
Ostensibly, we did this for a reason, such as to
‣
Measure a property (cross section, mass, etc.) of a known particle
●
Discover a new particle (pentaquarks, A , etc.)
● ￿
Set limits on something, e.g., the cross section of an undiscovered particle; that
●
is, we didn’t see it in a certain mass (or some other observable) range, so its
cross section (based on some model) must be less than X
We want to make a quantitative statement about the relationship
‣
between the experiment we conducted and the thing we set out to
measure (or detect) statistical inference
I’ll focus on discovery and setting limits
●
In those two cases, we want to answer
●
Did I discover something or not, and how can I demonstrate this?
•
What are the upper and lower limits on ___ of the particle I was looking for?
•
Both of these involve hypothesis testing and confidence intervals
●
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 3
Hypothesis Testing Center for
Cosmology and
Particle Physics
We start with a probability model likelihood function
Likelihood of what? Likelihood that the data set corresponds to the
‣
model parameters, θ .
i
‣ We’re actually testing hypotheses, H (null, SM, background-only)
0
and H (alternate, new physics, etc.)
1
Test statistic: A real-valued function that summarizes the data in a way
relevant to the hypotheses being tested
Neyman-Pearson lemma: The test statistic that minimizes the
‣
probability of accepting H when H is true, for a fixed CL, is
0 1
L ( x H ) which can be generalized to L(x θ )
0 0
| |
L(x H ) L(x θ )
1 best
| |
Separate parameters into
‣
Parameters of interest (physics parameters: mass, # signal events, etc.)
●
Nuisance parameters (everything else: background shape, etc.)
●
Nuisance parameters = systematics; we must deal with them somehow
●
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 4
Hypothesis Testing Center for
Cosmology and
Particle Physics
Want a test statistic that incorporates the nuisance parameters
Profile likelihood ratio
‣
ˆ
ˆ
L(x θ , θ )
r0 ν
λ = |
ˆ ˆ
L(x θ , θ )
r ν
|
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 5
Hypothesis Testing Center for
Cosmology and
Particle Physics
Want a test statistic that incorporates the nuisance parameters
Profile likelihood ratio
‣
Parameters of interest (POI),
ˆ
set to values for H ˆ
0
L(x θ , θ )
r0 ν
λ = |
ˆ ˆ
L(x θ , θ )
r ν
|
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 6
Hypothesis Testing Center for
Cosmology and
Particle Physics
Want a test statistic that incorporates the nuisance parameters
Profile likelihood ratio
‣
Conditional MLE of
Parameters of interest (POI),
nuisance parameters
ˆ
set to values for H ˆ
0 (i.e., for θ = θ )
L(x θ , θ ) r r0
r0 ν
λ = |
ˆ ˆ
L(x θ , θ )
r ν
|
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 7
Hypothesis Testing Center for
Cosmology and
Particle Physics
Want a test statistic that incorporates the nuisance parameters
Profile likelihood ratio
‣
Conditional MLE of
Parameters of interest (POI),
nuisance parameters
ˆ
set to values for H ˆ
0 (i.e., for θ = θ )
L(x θ , θ ) r r0
r0 ν
λ = |
ˆ ˆ
L(x θ , θ )
r ν
|
MLE of nuisance
MLE of POI
parameters
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 8
Hypothesis Testing Center for
Cosmology and
Particle Physics
Want a test statistic that incorporates the nuisance parameters
Profile likelihood ratio
‣
Conditional MLE of
Parameters of interest (POI),
nuisance parameters
ˆ
set to values for H ˆ
0 (i.e., for θ = θ )
L(x θ , θ ) r r0
r0 ν
λ = |
ˆ ˆ
L(x θ , θ )
r ν
|
MLE of nuisance
MLE of POI
parameters
A good choice: It’s the maximum likelihood under the H as a fraction of its
● 0
largest possible value; large values of λ indicate that H is reasonable
0
And, via Wilks’s Theorem, under certain conditions, 2 l o g λ is
‣
2 −
χ
asymptotically distributed as a with # d.o.f. = # POI
We can use it to calculate p-values and confidence intervals
●
Let’s look at a concrete example: APEX
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 9
APEX Example Center for
Cosmology and
Particle Physics
APEX TestA RPuEnX, T2e%st oRfu dna, t2a%, porfe dliamta. optics
2
c 450
V/
Analysis of APEX raw data e
M 400
1
s/ 350
t
invariant mass spectrum n
u
o 300
C
250
200
150
100
50
We want to
‣ 0
100 120 140 160 180 200 220 240 260 280 300
Invariant Mass (MeV/c2)
I ) Identify any statistically significant excesses in spectrum
●
• Search for small peaks of widths mass resolution
≤
2
II ) Set limits on A cross section, which scales as ￿ = α /α
● ￿ ￿
2
• Determine range in cross section (or ￿ ) of hypothetical narrow resonance
consistent with observed spectrum
‣ Spectrum of background-only = H (null hypothesis)
0
‣ Spectrum with significant small peak = H (alternate hypothesis)
1
‣ We first determine a probability model
James Beacham (NYU) Hall A Analysis Workshop, JLab, 8 Dec. 2010 APEX 10