
Combinatorics of free probability theory [Lecture notes] PDF
Preview Combinatorics of free probability theory [Lecture notes]
Combinatorics of free probability theory Roland Speicher Queen’s University, Kingston, Ontario Abstract. The following manuscript was written for my lec- turesatthespecialsemester’Freeprobabilitytheoryandoperator spaces’, IHP, Paris, 1999. A complementary series of lectures was given by A. Nica. It is planned to combine both manuscripts into abookA. Nica and R. Speicher: Lectures on the Combinatorics of Free Probability, which will be published by Cambridge University Press Contents Part 1. Basic concepts 5 Chapter 1. Basic concepts of non-commutative probability theory 7 1.1. Non-commutative probability spaces and distributions 7 1.2. Haar unitaries and semicircular elements 10 Chapter 2. Free random variables 17 2.1. Definition and basic properties of freeness 17 2.2. The group algebra of the free product of groups 21 2.3. The full Fock space 23 2.4. Construction of free products 27 Part 2. Cumulants 35 Chapter 3. Free cumulants 37 3.1. Motivation: Free central limit theorem 37 3.2. Non-crossing partitions 46 3.3. Posets and M¨obius inversion 50 3.4. Free cumulants 52 Chapter 4. Fundamental properties of free cumulants 59 4.1. Cumulants with products as entries 59 4.2. Freeness and vanishing of mixed cumulants 66 Chapter 5. Sums and products of free variables 75 5.1. Additive free convolution 75 5.2. Description of the product of free variables 84 5.3. Compression by a free projection 87 5.4. Compression by a free family of matrix units 91 Chapter 6. R-diagonal elements 95 6.1. Definition and basic properties of R-diagonal elements 95 6.2. The anti-commutator of free variables 103 6.3. Powers of R-diagonal elements 105 Chapter 7. Free Fisher information 109 7.1. Definition and basic properties 109 3 4 CONTENTS 7.2. Minimization problems 112 Part 3. Appendix 123 Chapter 8. Infinitely divisible distributions 125 8.1. General free limit theorem 125 8.2. Freely infinitely divisible distributions 127 Part 1 Basic concepts CHAPTER 1 Basic concepts of non-commutative probability theory 1.1. Non-commutative probability spaces and distributions Definition 1.1.1. 1) A non-commutative probability space (A,ϕ) consists of a unital algebra A and a linear functional ϕ : A → C; ϕ(1) = 1. 2) If in addition A is a ∗-algebra and ϕ fulfills ϕ(a∗) = ϕ(a) for all a ∈ A, then we call (A,ϕ) a ∗-probability space. 3) If A is a unital C∗-algebra and ϕ a state, then we call (A,ϕ) a C∗- probability space. 4) If A is a von Neumann algebra and ϕ a normal state, then we call (A,ϕ) a W∗-probability space. 5) A non-commutative probability space (A,ϕ) is said to be tracial if ϕ is a trace, i.e. it has the property that ϕ(ab) = ϕ(ba), for every a,b ∈ A. 6) Elements a ∈ A are called non-commutative random variables in (A,ϕ). 7) Let a ,...,a be random variables in some probability space (A,ϕ). 1 n If we denote by ChX ,...,X i the algebra generated freely by n non- 1 n commuting indeterminates X ,...,X , then the joint distribution 1 n µ of a ,...,a is given by the linear functional a1,...,an 1 n (1) µ : ChX ,...,X i → C a1,...,an 1 n which is determined by µ (X ...X ) := ϕ(a ...a ) a1,...,an i(1) i(k) i(1) i(k) for all k ∈ N and all 1 ≤ i(1),...,i(k) ≤ n. 8) Let a ,...,a be a family of random variables in some ∗-probability 1 n space (A,ϕ). If we denote by ChX ,X∗,...,X ,X∗i the algebra gener- 1 1 n n ated freely by 2n non-commuting indeterminates X ,X∗,...,X ,X∗, 1 1 n n then the joint ∗-distribution µ of a ,...,a is given by the a1,a∗1,...,an,a∗n 1 n linear functional (2) µ : ChX ,X∗,...,X ,X∗i → C a1,a∗1,...,an,a∗n 1 1 n n 7 8 1. BASIC CONCEPTS which is determined by µ (Xr(1)...Xr(k)) := ϕ(ar(1)...ar(k)) a1,a∗1,...,an,a∗n i(1) i(k) i(1) i(k) for all k ∈ N, all 1 ≤ i(1),...,i(k) ≤ n and all choices of r(1),...,r(k) ∈ {1,∗}. Examples 1.1.2. 1) Classical (=commutative) probability spaces fit into this frame as follows: Let (Ω,Q,P) be a probability space in the classical sense, i.e., Ω a set, Q a σ-field of measurable subsets of Ω and P a probability measure, then we take as A some suitable algebra of complex-valued functions on Ω – like A = L∞(Ω,P) or A = L∞−(Ω,P) := T Lp(Ω,P) – and p≤∞ Z ϕ(X) = X(ω)dP(ω) for random variables X : Ω → C. R Note that the fact P(Ω) = 1 corresponds to ϕ(1) = 1dP(ω) = P(Ω) = 1. 2) Typical non-commutative random variables are given as operators on Hilbert spaces: Let H be a Hilbert space and A = B(H) (or more generallyaC∗-orvonNeumannalgebra). Thenthefundamentalstates areoftheformϕ(a) = hη,aηi,whereη ∈ Hisavectorofnorm1. (Note that kηk = 1 corresponds to ϕ(1) = hη,1ηi = 1.) All states on a C∗-algebra can be written in this form, namely one has the following GNS-construction: Let A be a C∗-algebra and ϕ : A → C a state. Then there exists a representation π : A → B(H) on some Hilbert space H and a unit vector η ∈ H such that: ϕ(a) = hη,π(a)ηi. Remarks 1.1.3. 1)Ingeneral, thedistributionofnon-commutative random variables is just the collection of all possible joint moments of these variables. In the case of one normal variable, however, this collection of moments can be identified with a probability measure on C according to the following theorem: Let (A,ϕ) be a C∗-probability space and a ∈ A a normal random variable, i.e., aa∗ = a∗a. Then there exists a uniquely determined probability measure µ on the spectrum σ(a) ⊂ C, such that we have: Z ϕ(p(a,a∗)) = p(z,z¯)dµ(z) σ(a) for all polynomials p in two commuting variables, i.e. in particular Z ϕ(ana∗m) = znz¯mdµ(z) σ(a) 1.1. NON-COMMUTATIVE PROBABILITY SPACES AND DISTRIBUTIONS 9 for all n,m ∈ N. 2) We will usually identify for normal operators a the distribution µ a,a∗ with the probability measure µ. In particular, for a self-adjoint and bounded operator x, x = x∗ ∈ B(H), its distribution µ is a probability measure on R with compact x support. 3) Note that above correspondence between moments and probability measures relies (via Stone-Weierstrass) on the boundedness of the op- erator, i.e., the compactness of the spectrum. One can also assign a probability measure to unbounded operators, but this is not necessarily uniquely determined by the moments. 4) The distribution of a random variable contains also metric and al- gebraic information, if the considered state is faithful. Definition 1.1.4. A state ϕ on a ∗-algebra is called faithful if ϕ(aa∗) = 0 implies a = 0. Proposition 1.1.5. Let A be a C∗-algebra and ϕ : A → C a faithful state. Consider a self-adjoint x = x∗ ∈ A. Then we have (3) σ(x) = suppµ , x and thus also (4) kxk = max{|z| | z ∈ suppµ } x and (5) kxk = lim(cid:0)ϕ(xp)(cid:1)1/p. p→∞ Proposition 1.1.6. Let (A ,ϕ ) and (A ,ϕ ) be ∗-probability 1 1 2 2 spaces such that ϕ are ϕ are faithful. Furthermore, let a ,...,a in 1 2 1 n (A ,ϕ ) and b ,...,b in (A ,ϕ ) be random variables with the same 1 1 1 n 2 2 ∗-distribution, i.e., µ = µ . a1,a∗1,...,an,a∗n b1,b∗1,...,bn,b∗n 1) If A is generated as a ∗-algebra by a ,...,a and A is generated 1 1 n 2 as a ∗-algebra by b ,...,b , then 1 7→ 1, a 7→ b (i = 1,...,n) can be 1 n i i ∼ extended to a ∗-algebra isomorphism A = A . 1 2 2) If (A ,ϕ ) and (A ,ϕ ) are C∗-probability spaces such that A is as 1 1 2 2 1 C∗-algebra generated by a ,...,a and A is as C∗-algebra generated 1 n 2 ∼ by b ,...,b , then we have A = A via a 7→ b . 1 n 1 2 i i 3) If (A ,ϕ ) and (A ,ϕ ) are W∗-probability spaces such that A is 1 1 2 2 1 as von Neumann algebra generated by a ,...,a and A is as von 1 n 2 ∼ Neumann algebra generated by b ,...,b , then we have A = A via 1 n 1 2 a 7→ b . i i 10 1. BASIC CONCEPTS 1.2. Haar unitaries and semicircular elements Example 1.2.1. Let H be a Hilbert space with dim(H) = ∞ and orthonormal basis (e )∞ . We define the two-sided shift u by (k ∈ i i=−∞ Z) (6) ue = e and thus u∗e = e . k k+1 k k−1 We have uu∗ = u∗u = 1, i.e., u is unitary. Consider now the state ϕ(a) = he ,ae i. The distribution µ := µ is determined by (n ≥ 0) 0 0 u,u∗ ϕ(un) = he ,une i = he ,e i = δ 0 0 0 n n0 and ϕ(u∗n) = he ,u∗ne i = he ,e i = δ . 0 0 0 −n n0 Since u is normal, we can identify µ with a probability measure on σ(u) = T := {z ∈ C | |z| = 1}. This measure is the normalized Haar measure on T, i.e., dµ(z) = 1 dz. It is uniquely determined by 2π Z (7) zkdµ(z) = δ (k ∈ Z). k0 T Definition 1.2.2. A unitary element u in a ∗-probability space (A,ϕ) is called Haar unitary, if (8) ϕ(uk) = δ for all k ∈ Z. k0 Exercise 1.2.3. Let u be a Haar unitary in a ∗-probability space (A,ϕ). Verify that the distribution of u+u∗ is the arcsine law on the interval [−2,2], i.e. ( √1 dt, −2 ≤ t ≤ 2 (9) dµ (t) = π 4−t2 u+u∗ 0 otherwise. Example 1.2.4. Let H be a Hilbert space with dim(H) = ∞ and basis (e )∞ . The one-sided shift l is defined by i i=0 (10) le = e (n ≥ 0). n n+1 Its adjoint l∗ is thus given by (11) l∗e = e (n ≥ 1) n n−1 (12) l∗e = 0. 0 We have the relations (13) l∗l = 1 and ll∗ = 1−|e ihe |, 0 0
The list of books you might like

Shatter Me Complete Collection (Shatter Me; Destroy Me; Unravel Me; Fracture Me; Ignite Me)

The Sweetest Oblivion (Made Book 1)

The Spanish Love Deception

Corrupt (Devil's Night #1)

NASA Technical Reports Server (NTRS) 20060047744: Mated Flight Control Issues for Space Exploration Systems

Design of Observational Studies

Bölüm Oku

The Georgia Historical Quarterly 1993: Vol 77 Index

Bölüm Oku

A PRELIMINARY CHECKLIST OF THE VASCULAR PLANTS OF THE CHIQUIBUL FOREST, BELIZE

C. V. de Francisco Aguilar Piñal

International Law by George Fox Tucker and George Grafton Wilson
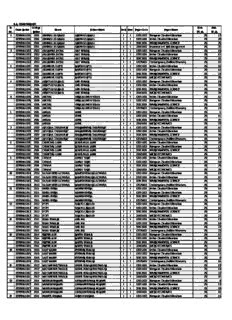
Sr. No. Exam Rollno College Rollno Name Father Name Part Sem Paper Code Paper Name Max

Together

Oracle Communications Session Border Controller Admin

Legislative Studies Quarterly 2006: Vol 31 Index

Psychiatry Research: Neuroimaging 1993: Vol 50 Index

Living with an Implanted Cardioverter Defibrillator (ICD)

DTIC ADA521722: Orchestrating Instruments of Power for Nationbuilding

Journal of Organometallic Chemistry 1993: Vol 448 Table of Contents




