CMOS Analog Circuit Design (2nd Ed.) Homework Solutions

509 Pages·2002·4.95 MB·English

CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 1
Chapter 1 Homework Solutions
1.1-1 Using Eq. (1) of Sec 1.1, give the base-10 value for the 5-bit binary number 11010
(b4 b3 b2 b1 b0 ordering).
From Eq. (1) of Sec 1.1 we have
N
b 2-1 + b 2-2 + b 2-3 + ...+ b 2-N =∑b 2-i
N-1 N-2 N-3 0 N-i
i=1
1 1 0 1 0
1 × 2-1 + 1× 2-2 + 0 × 2-3 + 1 × 2-4 + 0 × 2-5 = + + + +
2 4 8 16 32
16 + 8 + 0 + 2 + 0 26 13
= = =
32 32 16
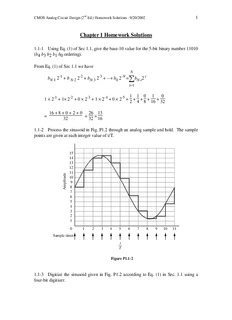
1.1-2 Process the sinusoid in Fig. P1.2 through an analog sample and hold. The sample
points are given at each integer value of t/T.
15
14
13
12
11
e
ud 10
plit 9
m
8
A
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11
Sample times
_ t_
T
Figure P1.1-2
1.1-3 Digitize the sinusoid given in Fig. P1.2 according to Eq. (1) in Sec. 1.1 using a
four-bit digitizer.
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 2
1111
15
1110
14
1101
13
12
1100
11
ude 10 1010
plit 9
m 8 1000 1000
A
7
0110
6
5
0101
4
0011
3
2 0010
0010
1
0 1 2 3 4 5 6 7 8 9 10 11
Sample times
_ t_
T
Figure P1.1-3
The figure illustrates the digitized result. At several places in the waveform, the digitized
value must resolve a sampled value that lies equally between two digital values. The
resulting digitized value could be either of the two values as illustrated in the list below.
Sample Time 4-bit Output
0 1000
1 1100
2 1110
3 1111 or 1110
4 1101
5 1010
6 0110
7 0011
8 0010 or 0001
9 0010
10 0101
11 1000
1.1-4 Use the nodal equation method to find v /v of Fig. P1.4.
out in
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 3
A B
R R
1 2
v R v g v R v
in 3 1 m 1 4 out
Figure P1.1-4
Node A:
0 = G (v -v ) + G (v ) + G (v - v )
1 1 in 3 1 2 1 out
v (G + G + G ) - G (v ) = G (v )
1 1 2 3 2 out 1 in
Node B:
0 = G (v -v ) + g (v ) + G ( v )
2 out 1 m1 1 4 out
v (g - G ) + v (G + G ) = 0
1 m1 2 out 2 4
 G +G +G G v 
1 2 3 1 in
 
g - G 0
 m1 2 
v =
out  G +G +G - G 
1 2 3 2
 
g - G G + G
 m1 2 2 4 
v G (G - g )
out 1 2 m1
=
v G G + G G + G G + G G + G G + G g
in 1 2 1 4 2 4 3 2 3 4 2 m1
1.1-5 Use the mesh equation method to find v /v of Fig. P1.4.
out in
R R
1 2
vin ia R3 v1 gmv1 R4 vout
ib ic
Figure P1.1-5
0 = -v + R (i + i + i ) + R (i )
in 1 a b c 3 a
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 4
0 = -v + R (i + i + i ) + R (i + i ) + v
in 1 a b c 2 b c out
v
out
i =
c R
4
i = g v = g i R
b m 1 m a 3
 v 
out
0 = -v + R i + g i R +  + R i
in 1 a m a 3 R 3 a
 4
 v   v 
out out
0 = -v + R i + g i R +  + R  g i R +  + v
in 1 a m a 3 R 2 m a 3 R out
 4  4
R
1
v = i (R + R + g R R ) + v
in a 1 3 m 1 2 out R
4
R + R + R 
1 2 4
v = i (R + g R R + g R R ) + v  
in a 1 m 1 3 m 2 3 out R
 4 
 R +R + g R R v 
1 3 m 1 3 in
 
R + g R R + g R R v
 1 m 1 3 m 2 3 in 
v =
out  R + R + g R R R / R 
1 3 m 1 3 1 4
 
R + g R R + g R R (R + R +R ) / R
 1 m 1 3 m 2 3 1 2 4 4 
v R R (1 - g R )
in 3 4 m 2
v =
out 2 2
(R + R + g R R ) (R + R + R ) - (R + g R R + g R R R )
1 3 m 1 3 1 2 4 1 m 1 3 m 1 2 3
v R R (1 - g R )
in 3 4 m 2
v =
out R R + R R + R R + R R + R R + g R R R
1 2 1 4 1 3 2 3 3 4 m 1 3 4
v R R (1 - g R )
out 3 4 m 2
=
v R R + R R + R R + R R + R R + g R R R
in 1 2 1 4 1 3 2 3 3 4 m 1 3 4
1.1-6 Use the source rearrangement and substitution concepts to simplify the circuit
shown in Fig. P1.6 and solve for i /i by making chain-type calculations only.
out in
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 5
i
R
2
i R v r i R i
in 1 1 m 3 out
i
R
2
i R v r i r i R i
in 1 1 m m 3 out
i
R
2
i R v R-r r i R i
in 1 1 m m 3 out
Figure P1.1-6
-r
m
i = i
out R
3
R
1
i = i
R + R - r in
1 m
i -r R /R
out m 1 3
=
i R + R - r
in 1 m
1.1-7 Find v /v and v /i of Fig. P1.7.
2 1 1 1
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 6
gm(v1-v2)
i
1
v R v
1 L 2
Figure P1.1-7
v
2
= g (v - v ) R
v m 1 2 L
1
v (1 + g R ) = g R v
2 m L m L 1
v g R
2 m L
=
v 1 + g R
1 m L
v = i R
2 1 L
substituting for v yields:
2
i R g R
1 L m L
=
v 1 + g R
1 m L
v R ( 1 + g R )
1 L m L
=
i g R
1 m L
v
1 1
= R +
i L g
1 m
1.1-8 Use the circuit-reduction technique to solve for v /v of Fig. P1.8.
out in
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 7
A (v - v )
v in 1
vin R1 v1 R2 vout
N N
1 2
A v A v
v 1 v in
vin R1 v1 R2 vout
Figure P1.1-8a
Multiply R by (A + 1)
1 v
A v
v in
vin v1 R2 vout
R (Av+1)
1
Figure P1.1-8b
-A v R
v in 2
v =
out R + R (A +1)
2 1 v
v -A R
out v 2
=
v R + R (A +1)
in 2 1 v
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 8
-A
v
R
v -A + 1 2
out v
=
v R
in 2
+ R
A + 1 1
v
As A approaches infinity,
v
v -R
out 2
=
v R
in 1
1.1-9 Use the Miller simplification concept to solve for v /v of Fig. A-3 (see
out in
Appendix A).
R R
1 3
r i
ma
v v
in R 1 v
2 out
i i
a b
Figure P1.1-9a (Figure A-3 Mesh analysis.)
v -r i -r
out m a m
K = = =
v i R R
1 a 2 2
R
3
Z =
1 r
m
1 +
R
2
-r
m
R
3 R
2
Z =
2 r
m
- - 1
R
2
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 9
R
3
r
m R R
2 3
Z = =
2 r R
m 2
+ 1 + 1
R r
2 m
R
1
r i
ma
vin R2 Z1 Z2 vout
i
a
Figure P1.1-9b
v (R || Z )
in 2 1  1 
i =  
a (R || Z ) + R R
2 1 1  2
v = -r i
out m a
-v r (R || Z )
in m 2 1  1 
v =  
out (R || Z ) + R R
2 1 1  2
v -r (R || Z )
out m 2 1  1 
=  
v (R || Z ) + R R
in 2 1 1  2
v -r R
out m 3
=
v (R R + R R + R r + R R )
in 1 2 1 3 1 m 2 3
1.1-10 Find v /i of Fig. A-12 and compare with the results of Example A-1.
out in
i R1 v1 R'2 R3 vout
in
g v
m 1
Figure P1.1-10
CMOS Analog Circuit Design (2nd Ed.) Homework Solutions : 9/20/2002 10
'
v = i (R || R )
1 in 1 2
'
v = -g v R = -g R i (R || R )
out m 1 3 m 3 in 1 2
v
out '
= -g R (R || R )
i m 3 1 2
in
R
' 2
R =
2 1 + g R
m 3
R R
1 2
1 + g R
' m 3
R || R =
1 2 (1 + g R ) R + R
m 3 1 2

1 + g R
m 3
R R
' 1 2
R || R =
1 2 (1 + g R ) R + R
m 3 1 2
v -g R R R
out m 1 2 3
=
i R + R + R + g R R
in 1 2 3 m 1 3
The A.1-1 result is:
v R R - g R R R
out 1 3 m 1 2 3
=
i R + R + R + g R R
in 1 2 3 m 1 3
if g R >> 1 then the results are the same.
m 2
1.1-11 Use the Miller simplification technique described in Appendix A to solve for the
output resistance, v /i , of Fig. P1.4. Calculate the output resistance not using the Miller
o o
simplification and compare your results.
R R
1 2
v R v g v R v
in 3 1 m 1 4 out
Figure P1.1-11a