Circular-Polarization Dependent Cyclotron Resonance in Large-Area Graphene in Ultrahigh Magnetic Fields

0.47 MB·English

by  L. G. Booshehri

Circular-Polarization Dependent Cyclotron Resonance in Large-Area Graphene in
Ultrahigh Magnetic Fields
L. G. Booshehri,1,2 C. H. Mielke,2 D. G. Rickel,2 S. A. Crooker,2 Q. Zhang,1 L. Ren,1 E. H. Ha´roz,1
A. Rustagi,3 C. J. Stanton,3 Z. Jin,4 Z. Sun,4 Z. Yan,4 J. M. Tour,4,5,6 and J. Kono1,7,
∗
1Department of Electrical and Computer Engineering, Rice University, Houston, Texas 77005
2National High Magnetic Field Laboratory, Los Alamos, New Mexico 87545
3Department of Physics, University of Florida, Gainesville, Florida, 32611
4Department of Chemistry, Rice University, Houston, Texas 77005
2
5Department of Computer Science, Rice University, Houston, Texas 77005
1
6Department of Mechanical Engineering and Materials Science, Rice University, Houston, Texas 77005
0
2 7Department of Physics and Astronomy, Rice University, Houston, Texas 77005
(Dated: January 17, 2012)
n
a Using ultrahigh magnetic fields up to 170 T and polarized midinfrared radiation with tunable
J wavelengthsfrom9.22to10.67µm,westudiedcyclotronresonanceinlarge-areagraphenegrownby

4 chemical vapor deposition. Circular-polarization dependent studies reveal strong p-typedoping for
1 as-grown graphene, and the dependence of the cyclotron resonance on radiation wavelength allows
for a determination of the Fermi energy. Thermal annealing shifts the Fermi energy to near the

] Diracpoint,resultinginthesimultaneousappearanceofholeandelectroncyclotronresonanceinthe
l
l magneticquantumlimit, eventhoughthesample isstill p-type,duetographene’slinear dispersion
a
anduniqueLandaulevelstructure. Thesehigh-fieldstudiesthereforeallowforaclearidentification
h
of cyclotron resonance features in large-area, low-mobility graphene samples.
-
s
e PACSnumbers: 78.67.Ch,63.22.+m,73.22.-f,78.67.-n
m
.
t The band structure of graphene exhibits a zero-gap the slope of the linear dispersions. Thus, different inter-
a
m linear dispersion relation near each of the Dirac points, Landau level (LL) transitions occur at different ener-
which results in a variety of exotic properties of two- gies or magnetic fields. Hence, the absence or presence
-
d dimensional (2D) Dirac fermions.1–3 While a number of a certain resonance can determine the Fermi energy.
n of electronic transport studies have revealed novel phe- Thisisinmarkedcontrasttoconventionalmaterialswith
o nomena in the presence of a high magnetic field, in- parabolicdispersions,whichformequallyspacedLLsina
c cluding half-integer quantum Hall states observed at magnetic field (E =(n+1/2)e~B/m , where m is the
[ n ∗ ∗
room temperature,1,2,4 magneto-optical properties are effective mass)and in whichall inter-LLtransitions (∆n

2 expectedtobeequallyunusual,5–15especiallyinthemag- = 1) occur at the same energies (for a given magnetic
v neticquantumlimit12wheretheFermilevelresidesinthe fiel±d) or at the same magnetic field (for a given probe
2
lowest Landau level (LL). Even in conventional 2D elec- photon energy).
2
tronsystemssuchasfoundinGaAsquantumwells,stud-
5 A number of CR measurements have been performed
4 iesofcyclotronresonance(CR)inthemagneticquantum on graphene,22–32 successfully resolving the unusual LL
. limit have shown many-body effects,16–19 such as spin-
0 structure, particularly when the graphene samples in-
splitting in the fractional quantum Hall regime, even
1 vestigated have relatively high mobilities, such as ex-
though CR is not expected to be sensitive to electron-
1 foliated graphene or epitaxial graphene on SiC. How-
1 electroninteractionsduetoKohn’stheorem.20Thelinear
ever, for technologically important applications requir-
: dispersionsofgrapheneautomaticallyevadethisbasicre-
v ing large-area graphene films grown via chemical vapor
quirementfor Kohn’stheorem, motivating CRstudies of
i deposition (CVD), we still face the current problem of
X graphene in ultrahigh magnetic fields.
lowmobilities ( 103 cm2V 1s 1), whichseverelybroad-
− −
ar An applied magnetic field (B) creates LLs for charge ens CR. Theref∼ore, for these low-mobility samples, CR
carriers both in the conduction and valence bands, and measurements must be explored within the regime of ul-
CR measures resonant optical transitions between ad- trahigh magnetic fields that makes the CR observabil-
jacent LLs (∆n = 1, where n is the Landau level ity condition ω τ > 1 achievable (here, ω is the cy-
± c c
index).21 CRisawell-establishedandpowerfultechnique clotron frequency and τ is the carrier scattering time).
to determine many fundamental parameters of a sam- Furthermore, a pulsed high-field magnet can be read-
ple, such as carrier effective masses, densities, mobilities ily combined with an infrared laser to perform CR mea-
and scattering rates. When performed with circularly surementswithcircularly-polarizedradiation,21,33 allow-
polarized radiation, the sign of the charge carriers can ing us to distinguish between electron-like and hole-like
also be determined. Furthermore, owing to graphene’s CR transitions. Magneto-spectroscopy using circularly-
nonparabolic(i.e., linear)dispersion,LLenergiesarenot polarized radiation indeed played a crucial role in elu-
equally spaced; rather, they follow E = c √2e~Bn, cidating electron and hole states in graphite.34–37 Fur-
n, ∗
where n 0 and c = 1.0 106 m/±s co±rresponds to thermore, a recent magneto-optical study on multilayer
∗
≥ ×
2
graphene on SiC using circularly-polarized radiation re- (a)
B = 170 Tesla
vealedmultipleCRcomponents,demonstratingtheexis-
tence of multiple species of carriers with different Fermi Circularly
2.3 MA
velocities.32 Polarized
Here,wepresentanexperimentalstudyofCRinCVD- Light
growngrapheneatultrahighmagnetic fields. Circularly-
polarizedmagneto-transmissionofCO laserlight(wave-
2
length λ = 9.22 µm to 10.7 µm) revealed a strong and
unintentional p-type (hole) doping of these nominally- 1.05
undoped graphene samples. A small CR feature at 10 T ] (b) l = 10.67 (cid:181)m 160
)
and a larger CR feature at 65 T corresponds to the n = 0 T = 300 K
(
0sittioonns, =res−pe1ctainvedlyn. =Wa−v1eletnognth-=dep−e2ndinentetr-mLLagntreatno-- )/BT 1.00 CERle cAtcrotinve 120 Ma
g
(
transmission data show a good agreement with calcu- T n
tlahteedsaLmLplteratonsbiteiodnest,eramlloinweidng(−th2e50FemrmeVi)e.nMerogryeo(vEeFr,)woef sion [ 0.95 (CHERoll eeInc Aatrccottniivv ee) 80 etic F
ftoournedmothveatphaynsniesaolribnegdtmheolgecruaplehsesnheiftssamthpeleFserinmivaencuerugmy mis 0.90 40 ield
tmoargkreadplhyecnleo’sserutnoiqtuheeDLiarnadcapuoilnetv(eEl Fstr=uc−tu34rem, ewVe).sDhouwe ans 0 (T)
r 0.85
thatinthemagneticquantumlimitthisallowsbothhole T 0 2 4 6

(n = 0 to n = 1) and electron (n = 0 to n = +1) CR Time (ms)
−
to be observed simultaneously, even though the sample
is still p-type. 1.02
(c)
We measured graphene samples grown via CVD on a 0)] 1.00
large-area ( 4 cm2) copper foil, resulting in the growth (
of large-are∼a, high-quality graphene.38 A poly (methyl )/T 0.98 Upsweep
methacrylate) (PMMA) film was spin-coated onto the B
graphene-coveredcopperfoilandwasheatedupto60 C (T 0.96
◦ [ 10 T

for 5 min to cure the PMMA film. Then the PMMA/ n 0.94
o
graphene layer was separated from the copper foil by si Downsweep
etching in a 1 M CuCl /6 M HCl aqueous solution and s 0.92
2 mi 65 T
was placed on the surface of Milli-Q water to remove
s 0.90
any water-soluble residues. The PMMA/ graphene film n
a
wasthentransferredontoathalliumbromoiodide(KRS- r 0.88
5) substrate, which is transparent at mid-infrared wave- T 0 40 80 120 160
lengths. The PMMA film wasdissolvedawayby soaking Magnetic Field (T)
the substrate in acetone for 8 hours,38 thus leaving only
the CVD-graphene sheets remaining on the KRS-5 sub-
strate.
FIG. 1: (color online) (a) Experimental configuration for
Transmission measurements were performed at room
magneto-transmission using the STC magnet. (b) Magneto-
temperature in the Faradaygeometry (where light prop-
transmission of 10.67 µm light through a nominally-undoped
agatesparalleltothemagneticfield),usingacontinuous-
CVD-grown graphene sample, during a 170 T magnet pulse.
wave, single-mode CO2 laser that is tunable from 9.2 Data for both circular polarizations are shown. The pro-
to 10.7 µm. The combination of a linear polarizer and nounced CR absorption that appears for “electron CR inac-
quarter-wave plate was used to switch between opposite tive” polarization indicates that the graphene is p-type(hole
circularpolarizations(historicallycalled“electronCRac- doped). (c) Electron CR inactive transmission versus mag-
tive” and “electron CR inactive”), and the transmission netic field shows two CR features at 10 T and 65 T, corre-
wasdetected with a mercurycadmium telluride detector spondington=0ton=−1andn=−1ton=−2inter-LL
transitions.
sensitive in the 2-12µm spectral range. The handedness
ofthe circularpolarizationanddirectionofthe magnetic
field were cross-checked via electron CR of bulk n-type
GaAs. long single-turn copper coil that discharges a maximum
To access ultrahigh magnetic fields, we used the Sin- currentof 4MAin 6µsandreachesmagneticfieldsin
∼ ∼
gle Turn Coil (STC) magnet at the National High Mag- excessof200Tduringstandardoperation. Thelargecur-
neticFieldLaboratory(NHMFL)inLosAlamos39,40(see rent, magnetic field, and associated Lorentz forces cause
Fig. 1a). The STC magnet combines a low-inductance, an outward,radial expansion (and eventual destruction)
60-kV capacitor bank with a 10-mm diameter, 10-mm of the copper coil within 15 µs. However, the sample
∼
3
and sample probe are not damaged, and repeated mea-
surements on the sample are possible. 1.00 (a)
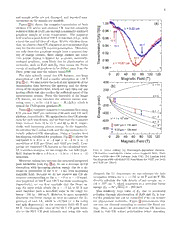
Figure 1(b) shows the magneto-transmission of both
l = 9.22 (cid:181)m
electron CR active and electron CR inactive circularly )] 0.98
0
polarizedlightat10.67µmthroughanominally-undoped (
T
graphene sample at room temperature. The magnetic )/ 0.96
B
fieldreachesapeakfieldof170Tinlessthan2.5µs,with ( 10 T
T
atotalriseandfalltimeof 6µs. Withinthistimedura-
tion,weobserveclearCRa∼bsorptionastransmissiondips n [ 0.94 15 T 80 T
o
onlyfortheelectronCRinactivepolarization. Therefore, si 0.92
not only does this graphene sample have a nonzero den- s
mi
sity of charge carriers, these charge carriers are holes.
s 0.90 65 T
This p-type doping is typical for as-grown, nominally- n
a l = 10.67 (cid:181)m
undoped graphene, most likely due to physisorption of r
T
molecules, such as H2O and O2, that causes the Fermi 0.88
energy ofundoped grapheneto be shifted awayfromthe
Dirac point and into the valence band.38,41 0 20 40 60 80 100 120
The data actually reveal two CR features, one large Magnetic Field (T)
absorption at 65 T and a smaller absorption at 10 T 400
∼ ∼
[Fig.1(c)]. Wealsonoticethelackofanyhysteresisofthe (b) n = +1
transmission data between the upsweep and the down-
200
sweepofthemagneticfield,whichnotonlyrulesoutany
heatingeffectsbutalsoverifiesthesufficientspeedofthe
0 n = 0
measurement system. From the linewidth of the larger
)
V
CR feature, we can calculate the effective carrier scat-
e
tering time, τ, to be 14 fs (ω τ = B /∆B ), which is m -200
c c c
typical for CVD-grown∼graphene.42 (

y
Figure2(a)comparesmagneto-transmissiondatausing g -400 n = -1
r
9.22µm and10.67µm radiation(134meV and116meV e
n n = -2
photons,respectively). WeagainobservetwoCRabsorp- E -600 c* = 1 x 106 m/s
tionsforeachwavelength,andwefindthattheresonance n = -3
fields increase from 10 to 15 T and 65 to 80 T, respec- 10.67 (cid:181)m = 116 meV n = -4
-800
tively, with increasing photon energy. In the Appendix,
9.22 (cid:181)m = 134 meV
wecalculatetheLandaulevelsandtheexpressionsforcir-
cularly polarized CR absorption. Using a Landau level 0 20 40 60 80 100 120
fandiagramcalculatedfor graphene,Fig.2(b)showsthe Magnetic Field (T)
calculated n = 0 to n = 1 and n = 1 to n = 2
− − −
transitions at 9.22 µm (blue) and 10.67 µm (red). Com-
paringourmeasuredCRfeaturestothecalculatedinter-
LL transitionenergies,we canassignthe low-field(high- FIG. 2: (color online) (a) Wavelength-dependent electron-
field)featuretothen=0ton= 1(n= 1ton= 2) CR-inactive transmission traces versus magnetic field. Each
− − −
transition. trace exhibits two CR features (hole CR). (b) Landau level
fandiagramwithcalculatedLLtransitionsfor10.67µm(red)
Moreover,takingintoaccountthemeasuredintegrated
and 9.22 µm (blue).
peak intensities from Fig. 2(a), we see a decrease in CR
absorption with increasing photon energy due to a de-
crease in population of the n = 1 LL with increasing
magnetic field. Because we do no−t observe any CR ab- alongside the LL degeneracy, we can estimate the hole
sorption corresponding to the n = 2 to n = 3 transi- occupation within the n= 1 LL at 65 T and 80 T. We
tion(expectedat103Tand135Tf−orthesewa−velengths, directly calculate the hole−density of our sample, nh =
respectively), we can first conclude that the Fermi en- 1.6 1012 cm−2, which translates to a zero-field Fermi
ergy EF must reside within the n =−1 LL at 65 T and ener×gy, EF = ~c∗√4πnh ≈ −295 meV.
must therefore have a zero-field value in the range be- This relatively large value of E due to accidental
F
tween 140 to 400 meV. However, to more accurately p-doping through physisorption of H O and O is typ-
2 2
− −
determine the Fermi energy, we need to consider the de- ical for graphene but can be controlled if we can remove
generacy of each LL, which is eB/2π~ ( 4 for valley the physisorbed molecules. Figure 3 demonstrates that
×
and spin degeneracy), at the resonance fields 65 T and one can use thermal annealing to control the Fermi en-
80 T. Calculating the ratio of the 65-T CR peak inten- ergy. Here, we measured CR with electron CR inactive
sity to the 80-T CR peak intensity and using this ratio (that is, hole CR active) polarization before annealing
4
200
1.02 (a) (c)
100 n = +1
1.00 0 n = 0
)
V
e -100 E (After) = -34 meV
n = -1 to -2 m F
0.98 y ( -200 E (Before) = -295 meV
] g F
)
(0 er -300 n = -1
/T 0.96 electron hole En
)B active active Before Annealing -400 n = -2
(T n = -4 n = -3
n [ (b) 0 10 20 30 40 50 60 70
o 1.01 Magnetic Field (T)
si
s
mi
1.00 (d)
s E
n
a
Tr 0.99
0 to +1 E ’ n = 0
0.98
F
0 to -1 After Annealing Annealing E DOS n = -1
0.97 F
n = -2
-40 0 40 80 120
n = -3
Magnetic Field (T) Valence Band
FIG.3: (coloronline) (a)Electron CR inactivetransmission at 10.6 µm before annealing, and (b)after annealing. (c)Landau
fandiagramshowingtheFermienergyoscillationwithmagneticfieldforbefore(blue)andafter(red)annealing,and(d)depicts
that annealing moves theFermi energy from −295 to −34 meV.
[Fig. 3(a)] and immediately after we annealed the sam- occupied states within the n = 0 LL to be 1:1.5. We
∼
ple for 2 hours at 150 C and 10 6 mbar to remove any can then use this ratio and the LL degeneracy to cal-
◦ −
physisorbedmolecules[Fig.3(b)]. AsshowninFig.3(b), culate the hole density of our sample after annealing to
the majority of the doped holes are removed during the be n = 2.1 1010 cm 2. As a result, we can deter-
h −
×
annealingprocess,andwenowseetwosmallerCRpeaks mine the zero-field Fermi energy after annealing to be
at +10 T and 10 T, corresponding to the n = 0 to E = 34 meV, again through E = ~c √4πn . Fig-
F F ∗ h
− −
n = 1 transition and the n = 0 to n = +1 transition, ure 3(c) shows the oscillations of the Fermi energy with
−
i.e., to hole and electron CR in the magnetic quantum increasingmagneticfieldforbothbefore(blue)andafter
limit. Note that, since the polarizationis hole CRactive (red) annealing. As Fig. 3(d) depicts, before annealing
forpositivemagneticfield,anyresonanceonthenegative the Fermi level sits within the n = 1 LL at 65 T and
−
magnetic field side is due to electron CR (note that the after annealing the Fermi energy now sits within the n
fieldswingsnegativeto about 40T followinga+170T = 0 LL at 10 T. The annealing process has successfully
−
pulse,allowingbothpositiveandnegativefieldstobeex- removedmostofthe physisorbedmoleculesthatp-doped
aminedinasinglepulse). Theemergenceofthetwo10T the graphene, leaving the system only slightly p-type.
peaks with opposite signs, andthe absence of the 60T Qualitatively similar thermal effects were observed for
∼
peak (the n= 1 to n= 2 transition), unambiguously other monolayer graphene samples that we investigated.
− −
demonstrate that the Fermi energy now resides in the n
Itshouldbeemphasizedherethatthesimultaneousap-
= 0 LL — the magnetic quantum limit — at 10 T.
pearanceofbothholeandelectronCRisanunusualphe-
Furthermore, as the integrated hole CR absorption is nomenon, made possible only via the unique electronic
strongerthanthe electronCRabsorption[see Fig. 3(b)], structure and Landau quantization of graphene. This
the graphene sample is still slightly p-type and the in- phenomenoncannotoccurinconventionalmaterialscon-
tensity ratio between the two peaks provides informa- taining only one carrier type. At B = 0, our graphene
tionabouttheratioofoccupiedversusunoccupiedstates samplesarestillslightlyp-typeevenafterannealing,and
within the n = 0 LL. More specifically, comparing the they contain only hole carriers. However, as soon as a
peakintensities,wecalculatetheratioofoccupiedtoun- finite magnetic field is applied, a Landau level with ex-
5
actly zero energy appears, i.e., the n = 0 Landau level Finally, this research was also made with Government
(4-fold degenerate due to valley and spin). This level support under and awarded by DoD, Air Force Office of
never moves with B in energy but simply grows in de- Scientific Research, National Defense Science and Engi-
generacy. As long as the Fermi energy lies within this neering Graduate (NDSEG), 32 CFR 168a. S.A.C. ac-
level, this level is partially filled, containing both holes knowledgessupportfromtheUCOPprogramonCarbon
and electrons, allowing the observation of both electron Nanostructures.
and hole CR even at T = 0.
Detailedcalculationsconfirmthese results. Inthe Ap-
pendix,wecomputetheCRabsorptionforbothelectron- Appendix: CALCULATION OF CYCLOTRON
active and hole-active circular polarizations. The results RESONANCE AND INTERBAND
MAGNETO-ABSORPTION FOR GRAPHENE
are givenby Eqs. (A.33) and (A.37). The results show a
number of interesting and unusual features that we have
discussed: i) The optical field Hamiltonian for graphene Here,wecalculatethecircularpolarizationdependence
comes in through an A σ term rather than the usual of the cyclotron resonance absorption of graphene in a
·
termA p;ii)theexpressionsshowthatevenanundoped magneticfield. WeuseCGSunitshereasopposedtothe
·
sample will show CR in contrast to conventional semi- textsothatwecancompareourexpressionstoothers. In
conductors where the sample must be doped; iii) if the addition,wecalculatethe interbandmagneto-absorption
Fermi energy lies in the n = 0 level, then CR is present (i.e., the valence band to conduction band transitions).
for both electron-activeandhole-activecircularpolariza- TheHamiltonianforgrapheneneartheKpointisgiven
tions;andiv)iftheFermilevelliesinthen=0level,the by
ratio of CR absorption between the electron-active and
0 k ik
hFoerlem-aiclteivveelpaenadkscaarlrlioewrsdoennesittyo.accurately determine the H =~c∗σ·k=~c∗(cid:18)kx+iky x−0 y(cid:19), (A.1)
Insummary,we havemeasuredcyclotronresonancein
where c is the Fermi velocity (and slope of the linear
graphene at ultrahigh magnetic fields. From polariza- ∗
dispersion), σ are the Pauli matrices and k is wavevec-
tion and wavelength dependent measurements, we have
shown unintentional chemical doping is strongly p-type tor measured from the K point k = kΓ −K (kΓ is the
wavevector measured from the Γ point). The energy
byobservingthen=0ton= 1andn= 1ton= 2
− − − eigenvalues for this Hamiltonian are
transitions in nominally-undoped graphene. Addition-
ally, we demonstrated that annealing effectively removes ε= ~c k. (A.2)
∗
p-doping from graphene,shifting the Fermi energy much ± | |
closer to the Dirac point. This shift completely blocked A similar Hamiltonian H = ~c σ k exists at the K
∗ ∗ ′ ′
then= 1ton= 2holecyclotronresonancetransition ·
pointbutwewillfocusonlyontheKpoint. Intheresults
− −
andrevealedthe n =0 to n=+1 electroncyclotronres-
for our final expressions, we simply add a factor of four
onance transition. As a result, due to graphene’s unique to account for both the spin degeneracy and the K,K
′
band structure, we simultaneously observed both hole
degeneracy.
and electron cyclotron resonance in the magnetic quan-
In the presence of an external field (DC magnetic or
tum limit, even with a p-type graphene sample. These
AC optical), one uses the Peierls substitution (minimal
high-fieldstudiesthereforeallowforaclearidentification coupling) k k+eA/~c (note the electron charge is
of cyclotron resonance features in large-area graphene →
e), where A is the vector potential, to yield
samples,and anaccuratedeterminationof their low car- −
rier mobilities and fast scattering times. eA
H =~c σ k+ . (A.3)
∗ ·(cid:18) ~c (cid:19)
Acknowledgments Todeterminethecyclotronresonanceandabsorption,we
will consider the case of both a DC magnetic field and
AC optical field so that the Hamiltonian becomes
This work was supported by the National Science
Foundation through Grant Nos. DMR-1006663, DMR-
eA eA
1105437, and OISE-0968405, the Department of Energy H =~c∗σ·(cid:18)k+ ~cB + ~copt(cid:19). (A.4)
BES Program through Grant No. DEFG02-06ER46308,
and the Robert A. Welch Foundation through Grant
The magnetic field will be oriented in the zˆ direction
No. C-1509. Work carried out at the National High
(perpendicular to the graphene layer), and we will use
Magnetic Field Laboratory – Pulsed Field Facility at
the Landau gauge in the form
Los Alamos National Laboratory was provided by fund-
ingfromtheNationalScienceFoundationthroughGrant A =(0,Bx,0). (A.5)
B
No. DMR-0654118 and from the Department of Energy
BES program, the State of Florida, and the Los Alamos For the AC optical field, we will take plane waves prop-
National Laboratory through the LDRD-DR program. agating in the zˆ direction (i.e., in the same direction as
6
the magnetic field). The vector potential A for the perturbation term is
opt
photon field can be related to the AC electric field by
eA iec
H1 =c∗σ opt = ∗ exp(iq r)
E =E exp[i(q r ωt)] (A.6) ·(cid:18) c (cid:19) − ω ·
opt 0
· −
cE 0 E iE
Aopt = iω0 exp[i(q·r−ωt)]. (A.7) ×(cid:18)Ex+iEy x−0 y(cid:19). (A.14)
Here q is in the zˆ direction and E can be left or right This is not the usual A p term that one uses in calcu-
0
·
circularlypolarizedinthex-yplane. WewritetheHamil- latingthe opticalpropertiesofconventionalsemiconduc-
tonian [Eq. (A.4)] as a sum of an unperturbed term and tors. Ifwe hadusedthe entire Hamiltonianforgraphene
′
a perturbation term instead of the Dirac approximation for the K and K
points we could have used an A p term in treating this
H =HB+H1, (A.8) interaction. ·
The optical matrix element corresponding to a transi-
where HB is the unperturbed Hamiltonian with only a tioncausedbytheperturbationterm(forin-planepolar-
DC magnetic field. This can be solved exactly by re- ization,i.e., qisalongthe z-direction)fromstatentom
placing k with ~ /i in Eq. (A.4) and keeping only the is calculated to be
∇
magnetic field term. The spectrum in the absence of the
iec
perturbation H1 is simply the Landau level spectra m,α,k H1 n,β,k = d2r ∗e(iqz)b b
′ m n
h | | i −ZZ ω ×
En,± =±γ√n, (A.9) (Φ∗m−1,k′,−αiΦ∗m,k′)(cid:18)Ex+0iEy Ex−0iEy(cid:19)(cid:18)ΦβinΦ−n1,,kk(cid:19).
where γ = √2lBc∗~ = c∗q2ec~B, n = 0,1,2..., and the (A.15)
magneticlength,l ,isgivenbyl = ~c/eB. Notethat
B B We note that n and m are 0 and that α,β = de-
theenergiesvarywith√nandalsowipth√B(throughthe ≥ ±
pending onwhetherthe stateisthe positiveenergystate
magnetic length). Note also that there is an n = 0 level.
(conduction band) or the negative energy state (valence
We can also write Eq. (A.9) in a simplified form
band). Cyclotron resonance absorption corresponds to
α=β and the inter-band magneto-absorptionto α=β.
En,± =±~ω0√n, (A.10) Forpositivecircularlypolarizedlight ,wehaveE6 0 =
⊕
E (xˆ+iyˆ)/√2 so that E = E /√2, E = iE /√2 and
with ω = √2c /l being the characteristic frequency. 0 x 0 y 0
0 ∗ B the matrix element becomes:
The wavefunctions are two-component spinors given by
iec
m,α,k H1 n,β,k = d2r ∗e(iqz)b b
Wehxt,ryea|tn,n±a,skip=osiΨtinv,e±(oxr,yz)er=obann(cid:18)d±ΦtihnΦ−e1n+,,kk(cid:19)si.gn(cAo.r1r1e)- ×h (Φ∗m−1′,k|′,−α|iΦ∗m,k′)i⊕(cid:18)βi−√2ZE0Z0Φn,k(cid:19)ω, (Am.16n)
sponds to the positive energy solution and the sign which integrates to
−
corresponds to the negative energy solution. The nor-
malization is given by m,α,k H1 n,β,k =β√2E0ec∗e(iqz)
′
h | | i⊕ ω
bn =(cid:26) 11 iiff nn==00 (A.12) ×bmbnδm−1,nδk,k′. (A.17)
√2 6
Using the Fermi Golden Rule, we can evaluate the tran-
and the component functions Φn are given by sition rate Wnm for an electron in state n going to an
unoccupied state m, n m
→
1 1 (x kl2)2
Φn.k = 2nn!√π LylBeikyexp(cid:18)− −2lB2B (cid:19) Wnm = 2~π|hm,α,k′ |H1 |n,β,ki|2δ(~ω−∆Enm,β,α),
(px kl2) p (A.18)
H − B , (A.13)
n
× (cid:18) l (cid:19)
B where ∆Em,α = E E . Taking into account the
n,β m,α − n,β
wdeitrhnΦ, a−n1d=0k, tHhen qbueainngtutmhenHumerbmeirteasPsooclyiantoemdiwalitohftohre- fpmro,αb)abtihliattytfhne,βsttahtaet(tmhe,αst)aitseu(nno,βcc)uispioecdc,utphieedtraanndsi(t1io−n
y motion in the Landau gauge. The wavefunctions in rate per unit volume is
Eq. (A.13) are harmonic oscillator wavefunctions in the
1 2π
x direction and plane waves in the y direction. R = m,α,k H1 n,β,k 2
We will treat the radiative Hamiltonian H1 perturba- n→m (cid:18)V (cid:19) ~ |h ′ | | i|
tively using the spinor wavefunctions in Eq.(A.11). The f (1 f )δ(~ω ∆Em,α). (A.19)
× n,β − m,α − n,β
7
We must also take into account the inverse process it follows that
(through emission of a photon), m n. The transition
→ 4 e2c 2
rate per unit volume is given by R = ∗ E2b2
⊕ L ~ω2l2 0 n
R = 1 2π n,β,k H1 m,α,k 2 z nXα≥,β0 B
m→n (cid:18)V (cid:19) ~ |h ′ | | i| (f f )δ(~ω ∆En+1,α), (A.27)
f (1 f )δ( ~ω+∆Em,α). (A.20) × n,β − n+1,α − n,β
× m,α − n,β − n,β
whereL isthethicknessofthegraphenelayer. Thetotal
z
The total net rate/volume is the difference between the power loss per unit volume is
two,
4 e2c 2
Rnm =Rn1→m2−πRm→n PL⊕ =R⊕~ω = Lz nX0 ωlB2∗ E02b2n
= m,α,k H1 n,β,k 2 α≥,β
(cid:18)V (cid:19) ~ |h ′ | | i| (f f )δ(~ω ∆En+1,α). (A.28)
(f f )δ(~ω ∆Em,α). × n,β − n+1,α − n,β
× n,β − m,α − n,β
(A.21) The absorption coefficient, αabs, is defined to be44
For undoped systems at T= 0, f = 1 and f = #of photons absorbed/unit volume second
0 for m > 0, i.e., all conduction bma,n−d states aremem,+pty αabs = #of photons injected/unit area ×second
×
and all valence bands states are occupied, while f0, = R R~ω
f0,+ =1/2. − = S/~ω = S , (A.29)
For positive circular polarized light,
whereS isthemagnitudeoftheaveragePoyntingvector:
4πe2c 2
Rm⊕n = V~ω2∗ E02b2mb2n n cE2
×(fn,β −fm,α)δm−1,nδk,k′δ(~ω−∆Enm,β,α). S =|hS(r,t)i|= r8π 0. (A.30)
(A.22)
Therefore, for positive circularly polarized light,
The total transition rate R summed over all possible
⊕ 8πe2c 2
transitions is α⊕abs =4 L ωl2n∗ cb2n
Rm⊕n = V4 Xmα,,βnXk,k′ 4π~eω2c2∗2E02b2mb2n[δm−1,nδk,k′]2 ×(fn,β −nXα≥f,βn0+1z,α)δB(~ωr −∆Enn,+β1,α). (A.31)
×(fn,β −fm,α)δ(~ω−∆Enm,β,α) We will set Lz = 1 to get the dimensionless absorption
4 2πe2c 2 per graphene layer. For cyclotron resonance, α = β,
= ∗ E2b2 and for positive circularly polarized light, the require-
V ~ω2 0 n
nX0Xk ment that
α≥,β
(f f )δ(~ω ∆En+1,α). ~ω =∆En+1,β =γ β√n+1 β√n >0 (A.32)
× n,β − n+1,α − n,β n,β −
(cid:0) (cid:1)
(A.23)
restricts the cyclotron resonance transitions to the elec-
tron (β = +) Landau levels and yields:
Thefactorof4comesfromthe2-foldspindegeneracyand
the 2-foldvalley degeneracy. Since the Landaulevelsare 16πe2c 2~ 2b2
sahbioftuetd harmonic oscillators in the x direction centered α⊕abs = nrclB2∗ nX0γ √n+1n−√n
≥ (cid:0) (cid:1)
x0 =klB2 (A.24) ×(fn,+−fn+1,+)δ(~ω−∆Enn,++1,+). (A.33)
and since the oscillatorcenter should be within the sam- If we account for scattering which results in linewidth
ple, following Roth43, we require that broadening, we can replace the delta function by a
Lorentzian:
0<x <L 0<k <L /l2. (A.25)
0 x ⇒ x B 1 ~τ 1
δ(~ω ∆En+1,α) −
Thisrestrictstheallowedvaluesofk. Convertingthesum − n,β → π(~ω ∆En+1,α)2+(~τ 1)2
over k into an integral − n,β −
1 ~τ 1
−
= ,
kmax Lydk = LyLx, (A.26) π(~ω−γα√n+1+γβ√n)2+(~τ−1)2
Xk →Z0 2π 2πlB2 (A.34)
8
yielding the expression: in a similar manner to obtain:
16πe2c 2~ 2b2 16πe2c 2~ 2b2
α⊕abs = nrclB2γ∗2 nX0 √n+1n−√n (fn,+−fn+1,+) α−abs = nrclB2∗ nX1γ √n−n√−1n−1
× γ2τ2 ~ω √nπγ+τ~≥1+(cid:0) √n 2+1. (cid:1) (A.35) ×(fn,−−fn−1,−)δ(≥~ω−(cid:0)∆Enn,−−1,−), (cid:1) (A.37)
~2 (cid:16) γ − (cid:17) To obtain the inter-band magneto-absorption (valence
band to conductionband), we use α=β and worryonly
This expression agrees with the results of Abergel and 6
about absorption (not emission) to get:
Fal’ko10(uptospinandvalleydegeneracy),whoobtained
these results using the Keldysh technique. 16πe2c 2~ 2b2
sitFiornosmdEepqe.n(dA.u3p3o),nw√eBse.eAthfaatcttohreosftrBengcothmoesftfhroemtrathne- α⊕abs = nrclB2∗ nX1γ √n+1n+√n
≥ (cid:0) (cid:1)
d1/aluB2 lteevremls)(wahnidchacfoamcteosrfroofm1/th√eBdecgoemneersacfryoomftthheeL1a/nω- ×(fn,−−fn+1,+)δ(~ω−∆Enn,+−1,+), (A.38)
dependence of Eq.(A.28) at the ω=ω √n resonance. and
0
Forcyclotronresonance(α=β)withnegativelycircu-
lpahrolytopnoalanrdizLedanlidgahut,letvheelsrelation between energy of the α−abs = 16nπrec2lcB2∗2~nX1γ √n2+b2n√−1n−1
≥ (cid:0) (cid:1)
~ω =∆Enn,−β1,β =γ β√n−1−β√n >0 (A.36) ×(fn,−−fn−1,+)δ(~ω−∆Enn,−−1,+). (A.39)
(cid:0) (cid:1)
requires that β = , i.e., only valence band transitions Note that the usual ∆n = 0 selection rule for the inter-
−
are allowed. One can repeat the calculation for the cy- band magneto-absorption now becomes ∆n = 1 de-
±
clotron resonance for negative circularly polarized light pending on the circular polarization.
∗ [e-mail]; www.ece.rice.edu/~kono; corresponding Semicond. Sci. Technol. 7, 1274 (1992).
author. 17 G. M. Summers, R. J. Warburton, J. G. Michels, R. J.
1 K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Nicholas, J. J. Harris, and C. T. Foxon, Phys. Rev. Lett.
M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and 70, 2150 (1993).
A. A.Firsov, Nature438, 197 (2005). 18 N.R.CooperandJ.T.Chalker,Phys.Rev.Lett.72,2057
2 Y.Zhang, Y.-W.Tan, H.L.Stormer,and P.Kim, Nature (1994).
438, 201 (2005). 19 K.AsanoandT.Ando,J.Phys.Soc.Jpn.65,1191(1996).
3 M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, Nat. 20 W. Kohn,Phys. Rev.123, 1242 (1961).
Phys. 2, 620 (2006). 21 J. Kono, in Methods in Materials Research, edited by
4 Y. Zhang, Z. Jiang, J. P. Small, M. S. Purewal, Y.-W. E. N. Kaufmann, R. Abbaschian, A. Bocarsly, C.-L.
Tan, M. Fazlollahi, J. D. Chudow, J. A. Jaszczak, H. L. Chien, D. Dollimore, B. Doyle, A. Goldman, R. Gronsky,
Stormer,and P.Kim,Phys.Rev.Lett.96, 136806 (2006). S.Pearton,andJ.Sanchez(JohnWiley&Sons,NewYork,
5 Y. Zhengand T. Ando,Phys. Rev.B 65, 245420 (2002). 2001), chap. 9b.2.
6 T. Ando, Y. Zheng, and H. Suzuura, J. Phys. Soc. Jpn. 22 M.L.Sadowski,G.Martinez,M.Potemski,C.Berger,and
71, 1318 (2002). W. A.de Heer, Phys.Rev.Lett. 97, 266405 (2006).
7 V. P. Gusynin and S. G. Sharapov, Phys. Rev. B 73, 23 Z. Jiang, E. A.Henriksen, L. C. Tung, Y.-J. Wang, M. E.
245411 (2006). Schwartz, M. Y. Han, P. Kim, and H. L. Stormer, Phys.
8 V. P. Gusynin,S. G. Sharapov, and J. P.Carbotte, Phys. Rev.Lett. 98, 197403 (2007).
Rev.Lett. 96, 256802 (2006). 24 R. S. Deacon, K.-C. Chuang, R. J. Nicholas, K. S.
9 A.Iyengar,J.Wang,H.A.Fertig,andL.Brey,Phys.Rev. Novoselov, and A. K. Geim, Phys. Rev. B 76, 081406
B 75, 125430 (2007). (2007).
10 D.S.L.AbergelandV.I.Fal’ko,Phys.Rev.B75,155430 25 E. A. Henriksen, Z. Jiang, L.-C. Tung, M. E. Schwartz,
(2007). M. Takita, Y.-J. Wang, P.Kim, and H. L.Stormer, Phys.
11 J. Milton Pereira, F. M. Peeters, and P. Vasilopoulos, Rev.Lett. 100, 087403 (2008).
Phys. Rev.B 76, 115419 (2007). 26 M. Orlita, C. Faugeras, P. Plochocka, P. Neugebauer,
12 V. P. Gusynin,S. G. Sharapov, and J. P.Carbotte, Phys. G. Martinez, D. K. Maude, A.-L. Barra, M. Sprinkle,
Rev.Lett. 98, 157402 (2007). C. Berger, W. A. de Heer, et al., Phys. Rev. Lett. 101,
13 M.KoshinoandT.Ando,Phys.Rev.B77,115313(2008). 267601 (2008).
14 Y. Barlas, R. Cˆot´e, K. Nomura, and A. H. MacDonald, 27 P. Neugebauer, M. Orlita, C. Faugeras, A.-L. Barra, and
Phys. Rev.Lett. 101, 097601 (2008). M. Potemski, Phys. Rev.Lett.103, 136403 (2009).
15 S. A.Mikhailov, Phys. Rev.B 79, 241309 (2009). 28 E. A. Henriksen, P. Cadden-Zimansky, Z. Jiang, Z. Q.
16 M.Besson,E.Gornik,C.M.Engelhardt,andG.Weimann, Li, L.-C. Tung, M. E. Schwartz, M. Takita, Y.-J. Wang,
9
P. Kim, and H. L. Stormer, Phys. Rev. Lett. 104, 067404 36 W. W.Toy,M. S. Dresselhaus, and G. Dresselhaus, Phys.
(2010). Rev.B 15, 4077 (1977).
29 I. Crassee, J. Levallois, A. L. Walter, M. Ostler, A. B. E. 37 R. E. Doezema, W. R. Datars, H. Schaber, and
Rotenberg, T. Seyller, D. van der Marel, and A. B. Kuz- A. VanSchyndel,Phys.Rev. B 19, 4224 (1979).
menko, NaturePhys. 7, 48 (2011). 38 Z. Jin, J. Yao, C. Kittrell, and J. M. Tour, ACS Nano 5,
30 A.M.Witowski,M.Orlita,R.St¸epniewski,A.Wysmol ek, 4112 (2011).
J. M. Baranowski, W. Strupin´ski, C. Faugeras, G. Mar- 39 C. H. Mielke and R. D. McDonald, in 2006 IEEE Inter-
tinez, and M. Potemski, Phys.Rev.B 82, 165305 (2010). national Conference on Megagauss Magnetic Field Gener-
31 M. Orlita, C. Faugeras, R. Grill, A. Wysmolek, ation and Related Topics (2006), vol. 5, pp.227–231.
W. Strupinski, C. Berger, W. A. de Heer, G. Martinez, 40 C.H.MielkeandB.Mircea,IEEETransactionsonPlasma
and M. Potemski, Phys.Rev.Lett. 107, 216603 (2011). Science 38, 1739 (2010).
32 I. Crassee, J. Levallois, D. van der Marel, A. L. Walter, 41 F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill,
T.Seyller,andA.B.Kuzmenko,Phys.Rev.B84,035103 P. Blake, M. I. Katsnelson, and K. S. Novoselov, Nat.
(2011). Mater. 6, 652 (2007).
33 J. Kono and N. Miura, in High Magnetic Fields: Sci- 42 Y.-W.Tan,Y.Zhang,K.Bolotin,Y.Zhao,S.Adam,E.H.
ence and Technology, Volume III,edited byN. Miura and Hwang, S. Das Sarma, H. L. Stormer, and P. Kim, Phys.
F. Herlach (World Scientific, Singapore, 2006), pp. 61–90, Rev.Lett. 99, 246803 (2007).
ISBN 981-02-4966-7. 43 L.M.Roth,B.Lax,andS.Zwerdling,Phys.Rev.114,90
34 P. R. Schroeder, M. S. Dresselhaus, and A. Javan, Phys. (1959).
Rev.Lett. 20, 1292 (1968). 44 S. L. Chuang, Physics of Optoelectronic Devices (Wiley,
35 H. Suematsu and S. Tanuma, J. Phys. Soc. Jpn. 33, 1619 New York,1995).
(1972).