
approximate reasoning using anytime algorithms PDF
Preview approximate reasoning using anytime algorithms
1 APPROXIMATE REASONING USING ANYTIME ALGORITHMS ShlomoZilbersteinandStuartRussell* DepartmentofComputerScience UniversityofMassachusetts,Amherst,MA01003 *DepartmentofEECS,ComputerScienceDivision UniversityofCalifornia,Berkeley,CA94720 ABSTRACT The complexityof reasoning in intelligent systemsmakes it undesirable, and some- times infeasible, to find the optimal action in every situation since the deliberation process itself degrades the performanceof the system. The problem is then to con- structintelligentsystemsthatreacttoasituationafterperformingthe“right”amount of thinking. It is by now widely accepted that a successful system must trade off decisionqualityagainstthecomputationalrequirementsofdecision-making. Anytime algorithms,introducedbyDean,Horvitzandothersinthelate1980’s,weredesigned tooffersuchatrade-off. Wehaveextendedtheirworktotheconstructionofcomplex systemsthatarecomposedofanytimealgorithms. Thispaperdescribesthecompila- tionandmonitoringmechanismsthatarerequiredtobuildintelligentsystemsthatcan efficientlycontroltheirdeliberationtime. Wepresenttheoreticalresultsshowingthat thecompilationandmonitoringproblemsare tractableinawiderangeofcases, and providetwoapplicationstoillustratetheideas. 1 INTRODUCTION A fundamental problem in computer science and artificial intelligence is the construction of systems that can operate robustly in a variety of real-time environments. A real-time environment can be characterized by a time- dependent utility function. In almost all cases, the deliberation required to select optimal actions will degrade the system’s overall utility. It is by now well-understood that a successful system must trade off decision quality for deliberationcost[1,12,14,19,21,22]. 1 2 (cid:0)(cid:2)(cid:1)(cid:4)(cid:3)(cid:6)(cid:5)(cid:8)(cid:7)(cid:10)(cid:9)(cid:12)(cid:11)(cid:14)(cid:13) The problem of deliberation cost has been widely discussed in artificial in- telligence, economics, engineering and philosophy. In artificial intelligence in particular, researchershave proposeda numberof meta-levelarchitectures to control the cost of base-level reasoning [4, 7, 9, 12, 18]. One promising approach is to use anytime [3] or flexible [10] algorithms, which allow the execution time to be specified, either as a parameter or by an interrupt, and exhibit a time/quality tradeoff defined by a performance profile. They pro- vide a simple means by which a system can control its deliberation without significantoverhead. Soonaftertheintroductionofanytimealgorithms,itbecameapparentthattheir compositionpresents a vital, non-trivial problem [3]. We show that modular composition of anytime algorithms can be achieved, hence the advantages of anytime algorithms can be extended to the design of complex real-time systems with many components. In standard algorithms, the fixed quality of the output allows for composition to be implemented by a simple call-return mechanism. Whenalgorithmshaveresourceallocationasadegreeoffreedom, and can be interrupted at any time, the situation becomes more complex. Consider the following simple example: a real-time medical expert system containing a diagnosis component which passes its results to a treatment- planningcomponent. Thefollowingissuesarise: 1. Howcantheindividualcomponentsbedesignedasanytimealgorithms? 2. How can their performance be described as a function of time and the natureoftheinputs? 3. How does the output quality of the treatment component depend on the accuracyofthediagnosisitreceives? 4. Whatsortofprogramminglanguageconstructsareneededtospecifyhow thesystemisbuiltfromitscomponents? 5. Foranygivenamountoftime,howshouldthattimebeallocatedtoeach ofthecomponents? 6. What if theconditionof thepatient suddenlyrequiresinterventionwhile the diagnosis component is still running and no treatment has been con- sidered? 7. How should the execution of the compositesystem be managed so as to optimize overall utility, particularlywhen the total execution time is not knowninadvance? ApproximateReasoningUsingAnytimeAlgorithms 3 In several publications, particularly [23], we address these issues in some depth. Here, we sketch our general approach, focusing in particular on the compilationproblem. Givenasystemcomposedofanytimealgorithms,com- pilation determines off-line the optimal allocationof time to the components for any given total allocation. The crucial meta-level knowledge for solving this problem is kept in the anytime library in the form of conditionalperfor- manceprofiles. Theseprofilescharacterizetheperformanceofeachelementary anytimealgorithmasafunctionofrun-timeandinputquality. In Section2, we define thebasic propertiesof anytimealgorithms. We show howtoconstructanytimealgorithmsandhowtocharacterizethetrade-offthat theyofferbetweenqualityofresultsandcomputationtime. Section3explains thebenefitsanddifficultiesinvolvedinthecompositionofanytimealgorithms. Sections 4 and 5 describe the two main components of our solution to the composition problem, namely off-line compilation and run-time monitoring. Section 6 describes briefly two applications of this approach. Finally, in Section 7, we summarize the benefits of our approach and discusses some directionsforfurtherworkinthisfield. 2 ANYTIMEALGORITHMS The term “anytime algorithm” was coined by Dean in the late 1980’s in the context of his work on time-dependent planning. Anytime algorithms are algorithms whose quality of results improves gradually as computation time increases,hencetheyofferatradeoffbetweenresourceconsumptionandoutput quality. Variousmetricscanbeusedtomeasurethequalityofaresultproducedbyan anytime algorithm. From a pragmatic point of view, it may seem useful to defineasingletypeofqualitymeasuretobeappliedtoallanytimealgorithms. Such a unifying approach may simplify the meta-level control. However, in practice,differenttypesofanytimealgorithmstendtoapproachtheexactresult incompletelydifferentways. Thefollowingmetricshavebeenproveduseful inanytimealgorithmconstruction: 1. Certainty – this metric reflects the degree of certainty that the result is correct. The degree of certainty can be expressed using probabilities, certaintyfactors,oranyotherapproach. 4 (cid:0)(cid:2)(cid:1)(cid:4)(cid:3)(cid:6)(cid:5)(cid:8)(cid:7)(cid:10)(cid:9)(cid:12)(cid:11)(cid:14)(cid:13) 2. Accuracy – this metric reflects a measure of the difference between the approximate result and the exact answer. Many anytime algorithms can provideaguaranteeaboundontheerror,wheretheboundisreducedover time. 3. Specificity – this metric reflects the level of detail of the result. In this case,theanytimealgorithmalwaysproducescorrectresults,butthelevel ofdetailisincreasedovertime. Many existing programming techniques produce useful anytime algorithms. Examplesincludeiterativedeepeningsearch,iterativeimprovementalgorithms innumericalcomputation,variableprecisionlogic,andrandomizedtechniques suchasMonteCarloalgorithmsorfingerprintingalgorithms. Forasurveyof suchprogrammingtechniquesandexamplesofalgorithmssee[23]. The notion of interrupted computationis almost as old as computationitself. Traditionally, interruptionwas used primarily for two purposes: aborting the executionof an algorithmwhose resultsare no longernecessary,or suspend- ing the execution of an algorithm for a short time because a computation of higher priority must be performed. Anytime algorithms offer a third type of interruption: interruption of the execution of an algorithm whose results are considered “good enough” by their consumer. Similar ideas motivated the developmentoftheCONCORDsystemforimprecisecomputation[15]. 2.1 Conditionalperformanceprofiles Toallowforefficientmeta-levelcontrolofanytimealgorithms,wecharacterize theirbehaviorbyconditionalperformanceprofiles(CPP)[24]. Aconditional performanceprofilecapturesthedependencyofoutputqualityontimealloca- tionaswellasoninputquality. In[23],thereadercanfindadetaileddiscussion of varioustypes of conditionalperformanceprofiles and their representation. To simplify the discussionof compilation, we will refer only to the expected CPPthatmapscomputationtimeandinputqualitytotheexpectoutputquality. Definition1 The conditional performance profile (CPP), of an algorithm (cid:0) is a function that maps input quality and (cid:1)(cid:3)(cid:2)(cid:4)(cid:2)(cid:6)(cid:5) (cid:7)(cid:9)(cid:8)(cid:11)(cid:10)(cid:13)(cid:12)(cid:15)(cid:14)(cid:17)(cid:16)(cid:19)(cid:18)(cid:21)(cid:20) (cid:8)(cid:23)(cid:22)(cid:25)(cid:24)(cid:27)(cid:26) computationtimetotheexpectedqualityoftheresults. ApproximateReasoningUsingAnytimeAlgorithms 5 q 1.00 0.90 0.80 0.70 0.60 0.50 0.40 0.30 0.20 0.10 0.00 0.00 1.00 2.00 3.00 4.00 t Figure1 GraphicalrepresentationofaCPP Figure1showsatypicalCPP.Eachcurverepresentstheexpectedoutputquality asafunctionoftimeforagiveninputquality. 2.2 Interruptibleandcontractalgorithms In [20] we make an important distinction between two types of anytime al- gorithms, namely interruptible and contract algorithms. An interruptible al- gorithm can be interrupted at any time to produce results whose quality is described by its performance profile. A contract algorithm offers a similar trade-off between computation time and quality of results, but it must know the total allocation of time in advance. If interrupted at any point before the termination of the contract time, it may yield no useful results. Interruptible algorithms are in many cases more appropriate for the application, but they are also more complicated to construct. In [20] we show that a simple, gen- eral construction can produce an interruptible version for any given contract algorithm. Furthermore, the interruptible algorithm requires at most sec- (cid:0)(cid:2)(cid:1) onds to produceresults of the qualityachievedby the contractalgorithmin (cid:1) seconds,forall . Thistheoremallowsustoconcentrateontheconstructionof (cid:1) contractalgorithmsforcomplexdecision-makingtasksandthenconvertthem intointerruptiblealgorithmsusingastandardtransformation. 6 (cid:0)(cid:2)(cid:1)(cid:4)(cid:3)(cid:6)(cid:5)(cid:8)(cid:7)(cid:10)(cid:9)(cid:12)(cid:11)(cid:14)(cid:13) speech recognizer classify speaker recognize utterance linguistic validity keyword meaning gender accent syntax Figure2 Acompositemoduleforspeechrecognition 3 COMPOSINGANYTIMEALGORITHMS Modularity is widely recognized as an important issue in system design and implementation. However,theuseofanytimealgorithmsasthecomponentsof amodularsystempresentsaspecialtypeofschedulingproblem. Thequestion is how much time to allocate to each component in order to maximize the outputqualityofthecompletesystem. Werefertothisproblemastheanytime algorithmcompositionproblem. Consider for example a speech recognition system whose structure is shown in Figure 2. Each box represents an elementary anytime algorithm whose conditional performance profile is given. The system is composed of three maincomponents. First,thespeakerisclassifiedintermsofgenderandaccent. Then a recognition algorithm suggests several possible matching utterances. Andfinally,thelinguisticvalidityofeachpossibleutteranceisdeterminedand thebestinterpretationisselected. Thecompositionproblemistheproblemof calculating how much time to allocate to each elementary component of the compositesystem,soastomaximizethequalityoftheutterancerecognition. Solving the composition problem is important for several reasons. First, it introduces a new kind of modularity into real-time system development by allowing for separation between the development of the performance com- ponents and the optimization of their performance. In traditional design of real-time systems, the performance components must meet certain time con- straintsthatarenotalwaysknownatdesigntime. Theresultisahand-tuning process that may, or may not, culminate with a working system. Anytime computation offers an alternative to this approach. By developing perfor- mancecomponentsthatareresponsivetoawiderangeoftimeallocations,one ApproximateReasoningUsingAnytimeAlgorithms 7 avoids the commitment to a particular performance level that might fail the system. The second reason why the composition problem is important relates to the difficulty of programming with anytime algorithms. To make a composite system optimal (or even executable), one must control the activation and interruptionofthecomponents. Insolvingthecompositionproblem,ourgoal istominimizetheresponsibilityoftheprogrammerregardingthisoptimization problem. Oursolutionisdescribedinthefollowingtwosections. 4 COMPILATION Given a system composed of anytime algorithms, the compilation process is designed to: (a) determine the optimal performance profile of the complete system;and(b)insertintothecompositemodulethenecessarycodetoachieve that performance. The precise definitionand solutionof the problem depend onthefollowingfactors: 1. Composite program structure – what type of programming operators areusedtocomposeanytimealgorithms? 2. Type of performance profiles – what kind of performance profiles are usedtocharacterizeelementaryanytimealgorithms? 3. Type of anytime algorithms – what type of elementary anytime algo- rithms are used as input? what type of anytime algorithm should the resultingsystembe? 4. Typeofmonitoring–whattypeofrun-timemonitoringisusedtoactivate andinterrupttheexecutionoftheelementarycomponents? 5. Qualityofintermediateresults–whataccessdoesthemonitoringcom- ponenthavetointermediateresults? istheactualqualityofanintermediate resultknowntothemonitor? Depending on these factors, different types of compilation and monitoring strategies are needed. To simplify the discussion in this paper, we will con- sideronlytheproblemofproducingcontractalgorithmswhentheconditional performance profiles of the components are given. We will assume that no 8 (cid:0)(cid:2)(cid:1)(cid:4)(cid:3)(cid:6)(cid:5)(cid:8)(cid:7)(cid:10)(cid:9)(cid:12)(cid:11)(cid:14)(cid:13) activemonitoringisallowedoncethesystemisactivated. Abroader,in-depth analysisofcompilationandmonitoringcanbefoundin[23]. Let be a setof anytimefunctions. Assumethat all functionparametersare (cid:0) passedby valueandthat functionshavenoside-effects(asinpurefunctional programming). Let be a set of input variables. Then, the notion of a (cid:1) compositeexpressionisdefinedasfollows: Definition2 Acompositeexpressionover withinput is: (cid:0) (cid:1) 1. An expression where is a functionof argumentsand (cid:2)(cid:4)(cid:3)(cid:6)(cid:5)(cid:8)(cid:7)(cid:10)(cid:9)(cid:12)(cid:11)(cid:13)(cid:11)(cid:14)(cid:11)(cid:13)(cid:9)(cid:8)(cid:5) (cid:16)(cid:15) (cid:2)(cid:18)(cid:17)(cid:19)(cid:0) (cid:20) (cid:12) . (cid:5) (cid:7) (cid:9)(cid:12)(cid:11)(cid:13)(cid:11)(cid:13)(cid:11)(cid:14)(cid:9)(cid:21)(cid:5) (cid:17)(cid:22)(cid:1) (cid:12) 2. Anexpression where isa functionof argumentsand (cid:2)(cid:4)(cid:3)(cid:24)(cid:23) (cid:7) (cid:9)(cid:25)(cid:11)(cid:14)(cid:11)(cid:13)(cid:11)(cid:13)(cid:9)(cid:26)(cid:23) (cid:15) (cid:2)(cid:27)(cid:17)(cid:28)(cid:0) (cid:20) (cid:12) each isacompositeexpressionoraninputvariable. (cid:23) (cid:10) Forexample,theexpression isacompositeexpressionover (cid:29)(cid:30)(cid:3) (cid:31)!(cid:3)#"$(cid:15)%(cid:9) (cid:22)(cid:3)(cid:6)&(cid:28)(cid:3)(cid:6)’((cid:15)(cid:21)(cid:15)(cid:8)(cid:15) ) with input ) . Supp(cid:1) ose that each function in has a con- (cid:29)*(cid:9)+(cid:31),(cid:9) -(cid:9)(cid:21)&/. "0(cid:9)(cid:21)’1. (cid:0) (cid:1) ditional performanceprofile associatedwith it that specifiesthe quality of its outputasafunctionoftimeallocationtothatfunctionandthequalitiesofitsin- puts. Givenacompositeexpressionofsize ,themainpartofthecompilation (cid:20) processistodetermineamapping: 2 (1.1) 3(cid:3) (cid:8)(cid:7)4(cid:9)(cid:12)(cid:11)(cid:13)(cid:11)(cid:13)(cid:11)(cid:14)(cid:9) (cid:16)(cid:15) (cid:7) (cid:1) (cid:20) (cid:1) (cid:1) (cid:12) This mapping determines for each total allocation, , the allocation to the (cid:1) componentsthatmaximizestheoutputquality. 4.1 Acompilationexample Letuslookfirstatasimpleexampleofcompilationinvolvingonlytwoanytime algorithms. Supposethatonealgorithmtakestheinputandproducesaninter- mediateresult. Thisresultisthenusedasinputtoanotheranytimealgorithm which, in turn, produces the final result. Many systems can be implemented by a compositionof a sequenceof two or more algorithms. For example, an automated repair system can be composed of two algorithms: diagnosis and treatment. Thiscanberepresentedingeneralbythefollowingexpression: 5-6 6 *; 6 (cid:0) (cid:0) 87 :9 (cid:3) (cid:7)<(cid:3)(cid:6)=>(cid:20)?7 (cid:26)(cid:15)(cid:8)(cid:15) (cid:1) (cid:1) (cid:1) ApproximateReasoningUsingAnytimeAlgorithms 9 Q Q 1 1 x Time t−x Time Figure3 Theperformanceprofilesof and (cid:0)(cid:2)(cid:1) (cid:0)(cid:4)(cid:3) Figure 3 shows the performance profiles of (cid:0) and (cid:0)*; . These performance (cid:7) profilesaredefinedby: (cid:5) (cid:5) ; (cid:7)(cid:10)(cid:3) (cid:1)(cid:8)(cid:15)(cid:7)(cid:6)(cid:9)(cid:8)(cid:11)(cid:10)(cid:13)(cid:12)(cid:15)(cid:14)(cid:17)(cid:16)(cid:19)(cid:18) (cid:26) (cid:3) (cid:1)(cid:8)(cid:15)(cid:20)(cid:6)(cid:21)(cid:8)(cid:11)(cid:10)(cid:13)(cid:12)(cid:15)(cid:14)(cid:17)(cid:16)(cid:23)(cid:22) (cid:26) Assumethattheoutputqualityisthesumofthequalitiesof (cid:0) and (cid:0)*; andis (cid:7) expressedby: (cid:5) (cid:3)(cid:6)" (cid:15)(cid:20)(cid:6)(cid:24)(cid:8)(cid:11)(cid:10)(cid:13)(cid:12)(cid:25)(cid:14)(cid:26)(cid:16)(cid:19)(cid:18)(cid:28)(cid:27)(cid:2)(cid:29)(cid:30)(cid:8)(cid:11)(cid:10)(cid:31)(cid:12)(cid:15)(cid:14)(cid:17)(cid:16)(cid:23)(cid:22)! (cid:26) (cid:14)"(cid:27)$# (1.2) Themaximalqualityisachievedwhen . Inotherwords: %$& (cid:6)(cid:30)’ % (cid:27) ( ( ; (1.3) (cid:7) (cid:12)(cid:15)(cid:14)(cid:26)(cid:16)$(cid:18))(cid:27)*(cid:10) (cid:12)(cid:15)(cid:14)(cid:17)(cid:16)(cid:23)(cid:22)+ (cid:26) (cid:14),(cid:27)(cid:23)#(cid:7)(cid:6)-’ The solution of this equation yields the following optimal time allocation mapping: .0/(cid:2)( .0/(cid:2)( ; ( ; .2/(cid:2)( ; .2/(cid:2)( ( 2 (cid:7)(cid:2)(cid:1)(cid:6)(cid:20)3(cid:3) (cid:7)1(cid:10)( (cid:7) (cid:29) ( ; (cid:29) (cid:1) (cid:9) (cid:10)( (cid:7) (cid:29) ((cid:7)(cid:20); (cid:29) (cid:7) (cid:1) (cid:15) (1.4) Tocompletethecompilationprocess,thecompilerneedstoinsertcodeinthe originalexpressionfor properactivationof (cid:0) (cid:7) and (cid:0) ; as contractalgorithms with the appropriate time allocation. This is done by replacing the simple function call by an anytime function call [23]. The implementation of an anytimefunctioncalldependsontheparticularprogrammingenvironmentand willnotbediscussedinthispaper. 4.2 Thecomplexityofcompilation The compilation problem is defined as an optimization problem, that is, a problem of finding a schedule of a set of components that yields maximal outputquality. Inordertoanalyzeitscomplexity,itismoreconvenienttorefer tothedecisionproblemvariantofthecompilationproblem. Givenacomposite 10 (cid:0)(cid:2)(cid:1)(cid:10)(cid:3) (cid:5)(cid:8)(cid:7)(cid:10)(cid:9)(cid:12)(cid:11)(cid:14)(cid:13) expression ,theconditionalperformanceprofilesofitscomponents,andatotal (cid:12) allocation , the decision problem is whether there exists a schedule of the (cid:31) components that yields output quality greater than or equal to . To begin, (cid:0) considerthegeneralproblemofglobalcompilationofcompositeexpressions, orGCCE.In[23],weprovethefollowingresult: Theorem3 TheGCCEproblemisNP-completeinthestrongsense. TheproofisbasedonareductionfromthePARTIALLYORDEREDKNAP- SACK problem which is known to be NP-completein the strong sense. The meaningofthisresultisthattheapplicationofthecompilationtechniquemay be limited to small programs. To address the complexity problem of global compilation,wehavedevelopedanefficientlocalcompilationtechnique. 4.3 Localcompilation Local compilation is the process of finding the best performance profile of a module based on the performance profiles of its immediate components. If those components are not elementary anytime algorithms, then their perfor- mance profiles are determined using local compilation. Local compilation replacestheglobaloptimizationproblemwithasetofsimpler,localoptimiza- tion problems and reduce the complexity of the whole problem. Unfortu- nately,localcompilationcannotbeappliedtoeverycompositeexpression. If theexpressionhasrepeatedsubexpressions,thencomputationtimeshouldbe allocated only once to evaluate all identical copies. Local compilation can- nothandlesuchcases. However,thefollowingthreeassumptionsmakelocal compilationbothefficientandoptimal[23]: 1. The tree-structured assumption – the input composite expression has norepeatedsubexpressions,thusitsDAG(directedacyclicgraph)repre- sentationisatree. 2. Theinput-monotonicityassumption–theoutputqualityofeachmodule increaseswhenthequalityoftheinputimproves. 3. Thebounded-degreeassumption–thenumberofinputstoeachmodule isboundedbyaconstant, . (cid:1)
Description:The list of books you might like

Shatter Me Complete Collection (Shatter Me; Destroy Me; Unravel Me; Fracture Me; Ignite Me)

Do Epic Shit

The Subtle Art of Not Giving a F*ck

Credence

El derecho explicado a los jóvenes

capoeira angola – danza de guerra

Ram Accelerators: Proceedings of the Third International Workshop on Ram Accelerators Held in Sendai, Japan, 16–18 July 1997

Burgen und Schlösser Natur aktiv Tag der Franken

Journal of Vascular Surgery 1993: Vol 17 Index

AMO Overview

C++ for You++, AP Edition

C++ för dig som kan Java

C9553 an Arabic a Colloquial Handbook in the Syrian Dialect

Detection of Ketenimine (CH2CNH) in SGRB2(N) Hot Cores

A new species of Tetralonia (Thygatina) from India, with notes on the Oriental fauna (Hymenoptera, Apidae)

The Outsider

The Fantasy Trip. Hexagram
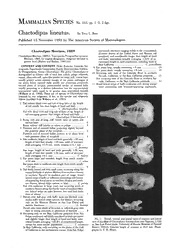
Chaetodipus lineatus

Developmental Brain Research 1993: Vol 74 Index





