Table Of ContentPaper Number: AIAA-2002-1761
FIELD-PROGRAMMABLE GATE ARRAY COMPUTER IN STRUCTURAL ANALYSIS: AN INITIAL
EXPLORATION
Robert C. Singleterry Jr., NASA Langley Research Center, Hampton, Virginia 1
Jaroslaw Sobieszczanski-Sobieski, AIAA F, NASA Langley Research Center, Hampton, Virginia
Samuel Brown, Star Bridge Systems Inc., Midvale Utah
Abstract 1. Introduction
This paper reports on an initial assessment of using As in other areas of applied mechanics, structural
aField-Programmable Gate Array (FPGA) analysis poses apersistent demand for faster
computational device asanew tool for solving computing. This is particularly true in applications
structural mechanics problems. A FPGA is an involving nonlinear behavior and in design optimization
assemblage of binary gates arranged in logical blocks because of the repetitive analysis. Until recently, the
that are interconnected via software in amanner computer hardware technology has responded to this
dependent on the algorithm being implemented and can demand via a two-prong development of faster
be reprogrammed thousands of times per second. In processors and concurrent processing with an
effect, this creates acomputer specialized for the increasing number of processors packaged either in a
problem that automatically exploits all the potential for single machine or distributed in a network.
parallel computing intrinsic in an algorithm. This The Field Programmable Gate Array (FPGA) is a
inherent parallelism is the most important feature of the relatively new addition to the above technology of
FPGA computational environment. It is therefore Massively Concurrent and Distributed Processing.
important that if aproblem offers achoice of different Relatively few engineers and scientists have had an
solution algorithms, an algorithm of ahigher degree of opportunity to explore the FPGA computers. This
inherent parallelism should be selected. paper reports on an initial assessment of the utility of
It is found that in structural analysis, an "analog the FPGA machine and its graphic programming
computer" style of programming, which solves language illustrated by a few simple examples in
problems by direct simulation of the terms in the
structures and dynamics. A variety of commercially
governing differential equations, yields a more available FPGA systems now exist. They are supplied
favorable solution algorithm than current solution
either as separate boards or as complete, turnkey
methods. This style of programming is facilitated by a systems. The information reported herein was obtained
"drag-and-drop" graphic programming language that is at the NASA Langley Research Center by using one
supplied with the particular type of FPGA computer such turnkey system containing 20 FPGA's called
reported in this paper. Simple examples in structural HAL-30 Hypercomputer TM (Reference [3]),
dynamics and statics illustrate the solution approach programmed with a graphic language VIVA ®
used. The FPGA system also allows linear scalability (Reference [2]), both from Star Bridge Systems ®. The
in computing capability. As the problem grows, the assessment includes a simplified description of the
number of FPGA chips can be increased with no loss of
salient features that distinguish the FPGA computer
computing efficiency due to data flow or algorithmic from single or multiple processor computers. The
latency that occurs when a single problem is distributed current merits and demerits of the FPGA computer and
among many conventional processors that operate in its future potential are discussed.
parallel.
This initial assessment finds the FPGA hardware
2. Conventional CPU vs FPGA
and software to be in their infancy in regard to the user
conveniences; however, they have enormous potential The kernel of most current computer architectures
for shrinking the elapsed time of structural analysis is the general purpose Central Processing Unit (CPU),
solutions if programmed with algorithms that exhibit programmed individually or in networked groups. The
inherent parallelism and linear scalability. This CPU itself consists of a large number of gates that work
potential warrants further development of FPGA- as on-off switches and are permanently wired in a
tailored algorithms for structural analysis. variety of fixed circuits that implement, in a binary-
logic framework, the whole gamut of functions needed
1Corresponding author: Robert C. Singleterry, Jr.; NASA Langley Research Center, MS 188B, Hampton VA 23681;
757-864-1437; r.c.singleterry @larc.nasa.gov
This paper is declared a work of the U.S. Government and is not subject to copyright protection in the United States
1
American Institute of Aeronautics and Astronautics
for its operation. At any particular time, only a small equals the number of gates supplied in the array. This
fraction of the total number of gates may be gainfully "inherently parallel" attribute allows all M operations to
employed, while the idle gates consume power and be executed at the same time, so that the maximum M is
generate heat. For engineers, the ability to generate only a function of the size and number of FPGAs
floating-point results is essential; therefore, some CPUs available.
have multiple floating-point units. In a massively
parallel environment that employs many CPUs, the 3. Graphic Programming of FPGA
number of floating-point results that can be generated
simultaneously is limited by the number of the CPUs, To make the multitude of gates available to the
user without performing machine-language level
the communication speed, and the memory capability,
all combined with the solution algorithm programming for each application, high-level languages
characteristics. exist, such as, HANDEL-C TM (Reference [1]), and
VIVA ®(Reference [2]), the latter having been used as a
In an FPGA, a command to execute a particular
basis for this report.
function is interpreted by the resident operating system
The authors' experiences to date indicate that the
to interconnect "by software" as many gates as
FPGA-based computers can benefit engineers in at least
necessary to perform that particular function and only
that function. The particular interconnection scheme two ways:
exists only as long as the job executes and can be 1. They exploit inherent parallelism in the algorithm
reconfigured to execute other functions many times per being executed, hence they have apotential to
second. In effect, a "specialized CPU" is created for radically reduce the computation elapsed time.
the job at hand. It isreminiscent of using an UV light 2. They may be programmed in an analog computer
source to burn-in the inter-gate conduits to implement a style that bypasses the need to develop solution
particular logic circuit, an operation known as algorithms to the equations that govern the
programming by "firmware". However, the result of problem.
this firmware programming is irreversible, while the These two points are illustrated by an introduction to
FPGA program can be changed by the user in the field - the VIVA language using simple examples.
-hence "Field" in FPGA. The VIVA language hides the tailoring of a
If the algorithm being implemented offers an specialized CPU from the amorphous supply of gates
opportunity to do M number of operations specifically for the job at hand under a veneer of a
simultaneously, then M specialized CPUs are being graphic language that enables coding by drawing what
created in the FPGA computer. In the extreme, the looks like a wiring diagram. In this regard, VIVA
specialized CPUs might all be different in terms of the extends to the FPGA machines the same approach that
number of gates and their interconnection logic if the languages such as MATLAB Simulink (Reference [4])
functions to be executed are different. Some of these implemented on a conventional, single or multiple
specialized CPUs could operate simultaneously and processor computers.
some could operate sequentially as required by the logic The essence of the VIVA graphic program is
of the algorithm being executed. Thus, the set of gates illustrated in Figure 1by the simple example of
computing a2for a given value of a.
available in an FPGA computer is viewed as aresource
for creating a computer tailored to the job at hand. In VIVA has a library of processing tools available in
principle, if the job is not large enough to use all the adisplay on right the margin of the screen. The tools
gates available, another unrelated job might be executed needed to execute the example problem are
simultaneously. Also, the hardware executes the entire 1. Input a from the user, illustrated by a horn on the
left
algorithm at once unless a sequencing step is part of the
algorithm, e.g., when the algorithm involves iterations. 2. Multiply (a *a), illustrated by the box with ×
To illustrate the computational parallelism afforded 3. Output a2to the user, illustrated by the horn on the
right
by a FPGA, consider the example of computing
These objects are dragged and dropped onto the main
a = b. c+ d. A conventional CPU needs two steps for
screen area and the inputs and outputs are connected to
this operation: first to calculate the product b. c and
the multiply object. The resulting diagram is
then to perform the sum because the steps are logically
"compilea_' into an executable code that can accept any
sequential. The FPGA potentially can complete both
value of a as input. The entire diagram may be named,
operations in one step provided the gates are properly
saved, turned into another icon in the library of tools,
configured. Furthermore, if the example is extended to
and displayed. In this manner, one can develop a
a = e. f + b. c + d, a FPGA still needs only one step
complex code by building blocks forming many
because it can engages more gates. This example can
hierarchically related levels. These building blocks
be extended in this manner while holding the execution
to a single step until the number of gates employed
2
American Institute of Aeronautics and Astronautics
workbesitfthealgorithmcanbemaderecursivine
velocity, and translation as functions of time computed
nature.
by VIVA for an impulse force excitation are presented
in Figure 6for a subcritical value of the damping
3.1 Equation Solution
constant. Should the damping be set to a negative
Now consider two algebraic equations with two
value, a divergent behavior reminiscent of wing flutter
unknowns y and z and six constants a, b, d, e, P, and M results.
3.3 Inclusion of non-linearitv
adyy ++ebzz ==MP (1)
A primary benefit of the analog computer
programming style is that the handling of non-linearity
One may program a VIVA solution using Cramer's
becomes almost trivial. For example, should the right
rule:
hand side of the first equation in Eq. (1) depend
Pe-Mb nonlinearly on the solution for y, Eq. (1) becomes
y=
ae-db
(2)
Ma- Pd ay +bz = P- ky2 (4)
Z-" dy + ez = M
ae -db
and the diagram in Figure 2 changes by the simple
and as in the previous example execute it in one step.
addition of the "Two DOF NL term" object shown in
However, expansion of the system of simultaneous
Figure 7. The numerical solution is obtained by
equations to larger number of variables causes
recording the output values ofy and z as the system
nonlinear explosion in the number of terms and
converges to a steady state. In effect the usual
operations that would quickly exhaust the FPGA
approach of devising a solution to the equations and
capacity and make the VIVA program exceedingly
then programming the solution is replaced by
complex. Therefore, a better method in VIVA is a
programming an iterative solution by directly
fixed-point iteration solution, as in Figure 2,
simulating the terms of the governing equations and
corresponding to
their connectivity. Table 1shows the results of the
above iterations along with results from a double
Yi = P- bzi-1 precision FORTRAN program, which agrees to six
a
(3) significant figures.
zi = M-dyi-1
e 3.4 Concurrent computing
To see the concurrent computing capability in the
Upon initialization, the system represented by the above application, consider alinear equation with only
diagram in Figure 2 converges to the fixed-point one unknown whose iterative solution may be written
as
(y=,Zoo) solution as the iterations are stepped through.
The need to iterate (with arate of convergence that (Xi_l)2-1
depends on the properties of the matrix of coefficients) Xi "- (5)
3
is the penalty for the solution simplicity. The flow of
execution within one cycle is: all the "divide" operators and the corresponding VIVA diagram in Figure 8. The
first, all the "multiply" operators next, followed by all reduced diagram amounts to one half of the diagram for
the "subtraction" operators. the system of two equations as in Eq. (1) shown in
Figure 2 (top left inset) and, yet, the execution time per
3.2 Analog programmin_ style iteration for the full system would be the same as for
The diagram in Figure 2is strikingly similar to a the reduced system because of the concurrent
processing.
wiring diagram one would have developed for this
problem when using an analog computer. The
similarity is more than superficial. It implies a style of 4. Initial Assessment of Experience with Statics and
programming based entirely on the now nearly Dynamics
forgotten analog computer methods. In fact, for a case
The next step is the application of alarger number
of a spring-mass vibrating system with damping shown
of degrees of freedom. Figure 9depicts asystem of
in Figure 3, one may revert to an analog computer
two vibrating masses with three springs, three dampers,
diagram from a more than 30-year-old reference [5,
and two governing, coupled differential equations. The
Figure 2-9] rendered in Figure 4 and derive from it the
corresponding analog computer wiring diagram is
VIVA diagram shown in Figure 5. The acceleration,
illustrated in Figure 10. A VIVA program based on
3
American Institute of Aeronautics and Astronautics
that diagram is shown in Figure 11with the program's labor and the amount of memory required to hold the
output shown in Figure 12. Again, if there were anon- intermediate results. This complexity stems from the
linearity in the system, for example, the k2 spring phenomenon of the sparse matrix filling-in with
stiffness were proportional to the spring elongation x2- nonzero terms in the direct solution process. The
xl, a simple modification shown by the inset in Figure number of the new, fill-in entries created in the process
10 would implement that non-linearity. of a sparse [K] matrix solution is, typically, of the
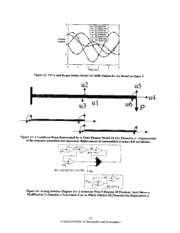
A cantilever beam in Figure 13provides an
order of 10 to 20 times the original number of nonzero
example of a static analysis case with multiple degrees entries.
of freedom. This simple case suggests a conclusion of
In general, the filling-in pattern cannot be precisely
general significance. The conclusion is that to use
predicted but reordering the degrees of freedom and the
FPGA's efficiently, one needs to select among the
associated reshuffling of the rows and columns in the
solution algorithms available, one that affords the
matrix can mitigate its detrimental effect on both the
largest degree of inherent parallelism. For the case at
amount of numerical labor and memory utilization.
hand, three possible algorithms to choose from are:
The graphic programming in VIVA does not lend itself
1. Forming the Load-Deflection equations
easily to the large, sparse matrix reordering. Even if it
[K]{u} = {P} and solving them by one of the did, that approach would still be unattractive because
direct solution methods, e.g., the Cholesky the experience shows that when the algorithms based on
decomposition algorithm. that approach are implemented on a multiprocessor
2. Solving the Load-Deflection equations by an computer, the interprocessor communication time
iterative method as in Figure 2. grows relative to the computing time. The resulting
3. Treating the beam as a quasi-dynamic system that loss of scalability brings in the law of diminishing
asymptotically tends to a solution corresponding to returns that limits the number of processors that may be
the static state.
used efficiently to well below 100 (Reference [7]). For
The above alternative algorithms have the following these reasons, Alternative 1does not appear to be the
merits and demerits.
best choice for an FPGA programmed by a pictorial
4.1 Direct solution methods language considering the currently available
information.
The direct solution approach is the least
advantageous in FPGA programming because it is a 4.2 Iterative solution methods
procedure, which consists mostly of the array An iterative scheme has an obvious advantage of
bookkeeping that exploits the [K] matrix sparseness. avoiding the filling-in phenomenon completely. In
Considering that in a large problem, only a few percent principle, one could assign a separate processor to each
of the [K] matrix entries may be nonzero, the equation, or even to each... + a_i*u i ... term in the
exploitation of sparseness is a necessity in problems of equations so that they all would be evaluated
any significance because processing of all the elements concurrently. That leaves the sparsity intact but does
including the null ones requires the number of generate data transfers that consume significant time.
arithmetical operations that is of order N3. On the other Furthermore, a separate and complete fixed-point
hand, that number reduces radically to order Nb2if one iterative process needs to be converged for each loading
exploits a banded structure of the matrix with the case whose number in practical applications may be in
bandwidth b. Exploitation of an irregular sparsity, thousands. Focusing on the positive, one iteration of a
measured by S equal to the ratio of the number of the [K] matrix, NxN, with sparseness S requires that the
nonzero elements in the matrix to N2,generates number of floating point multiplications be proportional
comparable or greater reduction. For example, for an to SN 2and all of them could be performed in the time
acoustic analysis reported in Reference [8] involving required by a single multiplication if a sufficient
millions of equations, it was observed that the growth in number of processors is available.
the number of arithmetical operations was reduced to On the other hand, if the number of iterations to
N4/3owing to the sparsity of the equation system. convergence is M and the number of loading cases isL,
However, that reduction is too problem dependent to be the total number of multiplications grows to SN2ML
expressed by a simple formula in terms of N and S. and the total elapsed time to execute them in an ideally
Elaborate schemes have been created to exploit concurrent processing grows in proportion to ML. It
efficiently the bandedness or irregular sparsity on single follows that the advantage of the iterative solution in
and multiprocessor computers (Reference [6]). These terms of the elapsed time decreases with the increase of
schemes although efficient and effective on today's the product ML and may vanish beyond a certain
computers are also complex as they employ critical threshold of that product. The value of M is
sophisticated bookkeeping and elaborate if-trees to find problem-dependent but should be expected to be large
a compromise between the minimum of the numerical because the [K] matrix conditioning that governs M is
4
American Institute of Aeronautics and Astronautics
knowntobepoor.ForexampleR,eferenc[6e]citesa
that the FPGA hardware capacity develops to that level,
casewith
N = 16000 that required M = 50000 for L =1. programming the FPGA using Alternative 3has a
It appears that implementation of an iterative potential for near perfect linear scalability of the
solution a large system of equations with exploitation of equation solution stage in static and dynamic structural
irregular sparsity is possible on a FPGA using VIVA. analysis. As abonus, this alternative is amenable to the
The language supports matrix operations by treating a simple implementation of a non-linearity as illustrated
matrix as one long vector and keeping track of the by inset in Figure 14.
element location indices. Therefore, the foregoing
assessment of the iterative solution, Alternative 2, 4.4 Computing time for operations other than
implemented on a multiprocessor computer applies to solving the load-deflection equations
FPGA as well. Therefore, one should consider Regardless of the load-deflection equation solution
Alternative 2, an iterative solution, as a viable one for method, the total elapsed time of astructural analysis in
FPGA up to a limit imposed by the product ML. any particular case is asum of the equation solution
time discussed above and the times consumed by the
4.30uasi-dynamic, step-by-step solution method
other stages in the total analysis process:
In Alternative 3, a structure such as the example of 1. development of afinite element model,
a cantilever beam represented by two finite element 2. assembly of the [K] matrix, and
portrayed in Figure 13 is treated as a dynamic system 3. interpretation of results.
solved by a step-by-step algorithm in time domain the The time of stage 1is primarily the human labor. To
same as the one used for the dynamic cases depicted in make aradical reduction using an FPGA based system,
Figures 3 and 9. To use that approach, one converts the the conventional finite element analysis would have to
structure to a dynamic system by adding inertia and be rewritten, starting from the very fundamentals and
damping. In case of the beam in Figure 13, that is tailoring the solution to the FPGA architecture.
accomplished by assuming fictitious mass and moment Regarding stage 3,the FPGA is being used for
of inertia associated with each of the unsupported visualization of voluminous data in non-engineering
degrees of freedom. Similarly, fictitious translational applications, so it is conceivable that it may assist at
and rotational dampers are attached to these degrees of that stage. For stage 2, the now-routine technique of
freedom. The magnitudes of the fictitious quantities are assembling the [K] matrix consists of selective
not important, except that for asymptotic convergence summing and placing the entries of the elemental
the damping coefficient values should be close to the stiffness matrices in the framework of [K]. That
critical ones. technique does not lend itself to efficient
The dynamic equation for the system so modified implementation in VIVA for the same reasons that were
reads
previously discussed in conjunction with Alternative 1.
That leaves an option of assembling [K] by the
[M]{ii} +[D]{u} + [K]{u} ={P(t)} (6)
textbook operation.
where matrices [M], [D], and [K] represent inertia,
[K] = [A]T[kdiag ] [A] (7)
damping, and stiffness.
Using amatrix-vector capability in VIVA the where [A] stands for the 0-1 connectivity matrix and
solution diagram for Eq. (6) shown in Figure 14 looks [k_ag] is the block-diagonal matrix of the unassembled
the same as one for asingle degree of freedom system structure. VIVA supports matrix operations so it could
except that the matrix operations replace the scalar execute Eq. (7); however, because the matrices
ones. When the loading {P(t)} advances in small involved aremostly zeros, it would be mandatory to
implement azero-bypass capability in the VIVA
increments from zero to {P(t)} in fictitious time the
language.
system converges to the static state of the displacement
Eventually, the FPGA capability may prove to be a
and stress under {P(t)}.
strong enough motivator for development of non-
Further experimentation is needed to determine conventional solution methods. One example of such
whether the number of increments for {P(t)} does not emerging methods whose intrinsic parallelism makes
them anatural match for FPGA is the cellular automata
have to grow with N for good convergence. If it does
method that has been demonstrated effective in
not, then the solution elapsed time would grow only
with the number of loading cases L and Alternative 3 structural analysis (Reference [9]) and in both analysis
would become better than Alternative 2 up to alimit and optimization in Reference [10].
governed by L and by the size of the FPGA. The pictorial programming in VIVA has the
Furthermore, the L limit can also be overcome if obvious advantage of being very intuitive. In computer
science community, there is no consensus whether that
the FPGA is large enough to carry the solution of Eq.
advantage can be sustained when the volume of detail
(6) for many loading cases simultaneously. Assuming
5
American Institute of Aeronautics and Astronautics
tobeseenbegintsoexceeodfwhaat singlescreemnay
developed in the past for the single processor,
displayT. heauthoresxperientcoedatereinforcewdith
sequential computing. The FPGA-based system is one
thegrowinguseofgraphicasyl stemssuchasReference
type of a computer on that path, and the methods
[4],indicatethsattheabilitytocollapsaesinglescreen
tailored to its architecture now will grow in their
diagramintoasingleicontobeusedasabuilding
effectiveness as the FPGA technology develops. The
blockinanothesrcreeinseffectivienkeepintghe
first exploratory step reported herein has but scratched
visuaclodecomplexituyndecrontrolI.tisroughly
the surface of the potential for this class of computers
equivalentotthegeneralalycceptegdoodpractice
and solution methods.
principleofstructurepdrogrammitnogkeepa
subroutinleengthtoonepage.
6. References
1. HANDEL-C at www.celoxica.com
5. Concluding Remarks
2. VIVA at www.starbridgesystems.com and are
Initial exploratory experience to date with a marks of Star Bridge Systems, Copyright 1998-
particular FPGA system, the VIVA/HAL-30 2001 by Star Bridge Systems, Inc.
software/hardware combination, has been reported and 3. HAL-15 at www.starbridgesystems.com and are
its merits and demerits assessed. Tentatively, on the marks of Star Bridge Systems, Copyright 1998-
negative side one should point to the lack of 2001 by Star Bridge Systems, Inc.
informative error messages, an effective debugger, and 4. SIMULINK at www.mathworks.com
absence of textual or graphic output rendering to a disk. 5. Michael G. Rekoff, Jr., Analog Computer
Considering that this FPGA technology is now in its Programming, Charles E. Merrill Books, Inc,
infancy, one may expect that these shortcomings will be Columbus, Ohio, 1967.
addressed as the VIVA product matures. On the 6. Nguyen, D. T.: Parallel-vector Equation Solvers for
positive side, the FPGA hardware/software system fully Finite Element Engineering Applications; Kluwer
exploits the solution algorithm's inherent parallelism, Academic Publ., 2002.
and no engineering time needs to be spent on devising 7. Storaasli, O.O.; Nguyen, D.T.; Baddourah, M.A.;
solutions to the governing equations. The problems of and Qin, J.: Computational Mechanics Analysis
scaling, precision, and stability faced by the analog Tools for Parallel Vector Supercomputers;
computer user in the past are absent owing to the digital Computing Systems in Engineering, Vol.4, N0:4-6,
accuracy and repeatability. However, the careful pp.349-354, Elsevier Publ. 1993.
choice of the time step in dynamic applications to stay 8. Watson, W.R.; and Storaasli, O.O.: Application of
within the problem's time scale is still required. NASA general purpose solver to large-scale
The analog programming style realizes best the computations in aeroacoustics; Advances in
FPGA potential in structural analysis. It offers a Engineering Software, No.31, pp.555-561.
potential to reduce the equation solving elapsed time, , Kim, P.; and Hajela, P.: Elastic Element Based
and an easy way to implement non-linearities. Cellular Automata Models in Structural Design; 4th
Extension of the FPGA utility to all the phases of a World Congress on Structural and
complete structural analysis process, will require Multidisciplinary Optimization, Dalian, China,
redevelopment from the ground up tailored to the June 2001.
FPGA architecture.
10. Abdalla, M.; and Gurdal, Z.: Structural Design
There is no doubt that computing technology has Using Optimality Based Cellular Automata; Paper
embarked on a path of inherent parallelism in AIAA-2002-1676; 43rdAIAA Structures,
processing that in due course will likely supplant many Dynamics, and Materials Conference; Denver, CO,
of the engineering physics solutions that were April 2002.
Table 1: Results of Fixed Point Iterations with Zo=3, Yo=2, a=P=l, b=d=0.5, M=0.0001
FORTRAN
VIVA K
(double " " - 10-13) (non-lineari:
Y= Z= Iterations y= Z=
1.3332667 -0.66653333 47 1.333267 -0.6665334
1.1553033 -0.57755163 69 1.155303 -0.5775517
6
American Institute of Aeronautics and Astronautics
asau,ared
!i!_iii!Z:ii!!::ii_i!iii:!!iii:i!iiiiii!:
Figure 1: Viva Algorithm to Calculate f(a) = a2
(Features left not explained are internal VIVA C
housekeeping details beyond the scope of this
report)
k
1 [cY_+ kx + f(t)]
m
Figure 3: Frictionless Mass and Spring with Damper
7
American Institute of Aeronautics and Astronautics
d2 dt2
X
f(t)
multiplier (amplifier)
integrator adder
-critical damping coefficient; natural vibration circular
(,On -
frequency;
Figure 4: Analog Computer Diagram corresponding to the System in Figure 3; It is Directly Translatable into
the Viva Algorithm in Figure 5
:_i_-_;&,; ----:_i-.......= _"-_:i::E__i::::.__i •:..::.:::..::::._._...................
15 Xo = Vo= to= 0
dt = 0.125 -- Position II
Step infirst dt -- Velocity
Impluse =125.0
iiil ;i'::i:!!:i!"'.::i 10 _k-......Damplng=O.5 ....................................... -- A_cceleration ......
= .
Arbitrary
0
-lO
:i:/iii:i/:i:i!.
0 2 4 Time 6 8 10
Figure 5: Viva Algorithm to Solve the Mass and
Spring with Dampers from Figure 3
Figure 6: Plotted Output from the Viva Algorithm
in Figure 5
8
American Institute of Aeronautics and Astronautics
!i:!ii%iiii!ii
i!iii!:i!!!ii!:_i
Figure 8: Viva Algorithm to Solve Equation (5) Via
the Fixed Point Algorithm for One Degree of
Freedom
Figure 7: Viva Algorithm to Solve Equation (4) Via
the Fixed Point Algorithm with a Non-linearity
X
C1 C2 C3
k
k2 k3
1
[C2X 2 -_- k2x 2 -- (C1 -_- C2)X 1 -(k 1 + k2)Xl]
m 1
1
[C2X 1 "_"k2x 1 -- (C2 -[- C3)'X 2 -- (k2 + k3)x2]
m 2
Figure 9: Two Masses Connected by Three Springs with Three Dampers on a Frictionless Surface
9
American Institute of Aeronautics and Astronautics
1/(ml)
.f(t)
w'!
> J
c2
1/(m2)
Figure 10: Analog Equivalent Wiring Diagram to Solve System in Figure 9
=_ __',H _o4 /
_w
_ I__:
Figure 11: Viva Algorithm to Implement Figure 10
10
American Institute of Aeronautics and Astronautics