The Probability Density of the Higgs Boson Mass

3 Pages·0.12 MB·English

by  Jens Erler

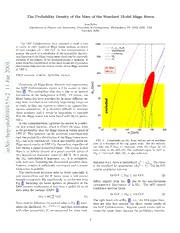
The Probability Density of the Mass of the Standard Model Higgs Boson
Jens Erler
Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, PA 19104-6396, USA
(October 2000)
The LEP Collaborations have reported a small excess 1000
of events in their combined Higgs boson analysis at center Γ, σ , R, R
of mass energies √s ∼< 208 GeV. In this communication, I asZymhamdetrliesq
presenttheresult of acalculation oftheprobability distribu- ν scattering
tionfunctionoftheHiggsbosonmasswhichcanberigorously 500 M
W
obtained ifthevalidityoftheStandardModelisassumed. It mt
1 arisesfromthecombinationofthemostrecentsetofprecision
0 electroweakdataandthecurrentresultsoftheHiggssearches
0 all data
at LEP 2.
2 90% CL
200
n PACS numbers: 14.80.Bn, 12.15.Mm, 12.15.Ji.
a
J
1 Combining all Higgs decay channels and experiments, eV] 100
1 the LEP Collaborations report a 2.5σ excess in their G
data [1]. The probability that this is due to an upward M [H
2
fluctuation of the background is 0.6%. Of course, the
v
Higgs boson has been searched for in many different en- 50
3 d
5 ergybins,andthereisaninfinitelylargeenergyrangeout de
1 of reach, so that one expects to observe an upward fluc- u
l
0 tuation somewhere. It is therefore difficult to interpret c
x
1 these numbers, and it would be imprudent to conclude e
0 that the Higgs boson has been found with 99.4% proba- 20
0
/ bility.
h
Inthiscommunication,Ipresenttheanswertoadiffer-
p
ent but related question, which is Given the data, what
- 10
p is the probabilitythatthe Higgsbosonis within reachof 100 120 140 160 180 200
e LEP 2? This question can be answered unambiguously mt [GeV]
h
oncetheprobabilitydistributionoftheHiggsbosonmass,
:
v MH,hasbeenconstructed. Thisisnotpossiblegiventhe FIG.1. Constraints on MH from varioussets of precision
Xi HiggssearchresultsatLEP2bythemselves,regardlessof data as a function of the top quark mass. For the individ-
ual data sets I show 1σ contours, while the ellipse for all
howstrongasignalis observedthere. The reasonis that
r
a there is an infinite domain of a priori possible values of data refers to the 90% CL. The excluded region by LEP 2,
M beyond the kinematic reach of LEP 2. As a result, MH <113.2 GeV (95% CL), is also indicated.
H
the M distribution is improper, i.e., it is asymptoti-
H
cally non-zero. Including the electroweakprecisiondata, mizationw.r.t.theseisunderstood,χ2 χ2 . Theerror
≡ min
however, renders it sufficiently convergent and a proper is the standard 1σ uncertainty (∆χ2 = 1). The 68.27%
integration is possible. central confidence interval,
The electroweak precision data by itself, especially Z
pole asymmetries and the W boson mass, is now precise 53 GeV MH 131 GeV, (2)
≤ ≤
enoughtoconstrainM significantly,ascanbeseenfrom
H differs slightly from Eq. (1) due to the non-Gaussian
Fig. 1. Including the latest updates as presented at the
(asymmetric) distribution of lnM . The 90% central
2000 summer conferences, I find from a global fit to all H
confidence interval yields,
data using the package GAPP [2],
38 GeV M 173 GeV. (3)
M =86+48 GeV. (1) ≤ H ≤
H −32
The righthandside ofEq.(3), i.e., the 95%upper limit,
Note,thatbydefinitionthecentralvalueinEq.(1)maxi- does not take into account the direct search results of
mizesthelikelihood,Ne−χ2(MH)/2,andthatcorrelations the LEP Collaborations. Negative search results will in-
with other parameters, ξi, are accounted for, since mini- crease the upper limit, because the probability distribu-
1
tion function is effectively being renormalized. For ex- This choice corresponds to a flat prior in the variable
ample,inapreviousanalysis[3]wefoundthatthe Higgs lnM , and there are various ways to justify it [7]. One
H
exclusioncurve presentedby the LEP Collaborationsin- rationale is that a flat distribution is most natural for a
creased the 95% upper limit by 30 GeV. variable defined over all the real numbers. This is the
The use of the Higgs exclusion curve, however, is only case for lnM but not M2. Also, it seems that a priori
H H
appropriate if no indication of an excess is observed. In it is equally likely that M lies, say, between 30 and
H
general,it is more appropriate to consider the likelihood 40 GeV, or between 300 and 400 GeV. In any case, the
ratio for the data, sensitivityoftheposteriortothe(non-informative)prior
diminishes rapidly with the inclusion of more data. As
(datasignal+background)
Q = L | , (4) discussed before, p(MH) is an improper prior but the
LEP 2
(databackground) likelihood constructed from the precision measurements
L |
will provide a proper posterior.
whereboththenumeratorandthedenominatorarefunc-
Occasionally,the Bayesianmethod is criticized for the
tions of M . The quantity,
H need of a prior, which would introduce unnecessary sub-
∆χ2(direct) 2lnQ (5) jectivity into the analysis. Indeed, care and good judge-
LEP 2
≡− ment is needed, but the same is true for the likelihood
can then be added to the χ2-function obtained from the model,whichhastobespecifiedinanystatisticalmodel.
precision data. If the signal hypothesis gives a better Moreover, it is appreciated among Bayesian practition-
(worse)descriptionofthedatathanthebackgroundonly ers, that the explicit presence of the prior can be advan-
hypothesis we find a negative (positive) contribution to tageous: it manifests model assumptions and allows for
the total χ2. Note, that this is a consistent treatment sensitivity checks. From the theorem (6) it is also clear
also in the case of a large downward fluctuation of the thatanyothermethodmustcorrespond,mathematically,
background or even if no events are observedat all. Use tospecific choicesforthe prior. Thus,Bayesianmethods
of Q had been originally advocated in Ref. [5] (see are more general and differ rather in attitude: by their
LEP 2
Eq. (23) in that reference). strong emphasis on the entire posterior distribution and
This treatment can be rigorously justified within the by their first principles setup.
framework of Bayesian statistics [6,7], which is particu- Including QLEP 2 in this way, one obtains the 95%
larlysuited for parameterestimation. Bayesianmethods CL upper limit MH 201 GeV, i.e. notwithstanding
≤
are based on Bayes theorem [6], the observed excess events, the information provided by
the Higgs searches at LEP 2 increase the upper limit by
p(dataM )p(M ) 28 GeV.
p(M data)= | H H , (6)
H| p(data) Given extra parameters, ξi, the distribution func-
tion of M is defined as the marginal distribution,
H
awnhdicphrmiourstdibsetrsibautitsifioend, opn(MceHth),ealirkeeslipheocoifide,dp.(dpa(tdaa|Mta)H≡), pli(hMooHd|dfaacttao)ri=zesR,pp((MMHH,,ξξii|)d=atap)(MQHip)(pξ(iξ)id)ξ,it.heIfξtihdeepliekne--
Rthpe(pdraotpa|eMrnHo)rpm(MaliHza)dtiMonHofinthtehpeosdteenrioomridniasttorribuptrioovnidoens dmeantceelyc)amnubletiviganrioarteed.noIrfmnaolt,,tbhuetnp(ξi|MH) is (approxi-
the left hand side. Depending on the case at hand, the
prior can χ2(M ,ξi)=χ2 (M )+
H min H
1. contain additional information not included in the 1∂2χ2(M )
H (ξi ξi (M ))(ξj ξj (M )).
likelihood model, 2 ∂ξ ∂ξ − min H − min H
i j
2. containlikelihoodfunctionsobtainedfromprevious The latter applies to our case, where ξi =
measurements, (m ,α ,α(M )). Integration yields,
t s Z
3. or be chosen non-informative. p(M data) √detEe−χ2min(MH)/2, (9)
H
| ∼
Of course, the posterior does not depend on how infor-
mationis separatedinto the likelihoodandthe prior. As wheretheξi errormatrix,E =(∂2χ2(MH))−1,introduces
∂ξi∂ξj
for the present case, I choose the informative prior, a correction factor with a mild M dependence. It cor-
H
responds to a shift relative to the standard likelihood
p(MH)=QLEP 2 pnon−inf(MH), (7) model, χ2(MH)=χ2min(MH)+∆χ2(MH), where
wherethenon-informativepartofthepriorwillbechosen detE(M )
∆χ2(M ) ln H . (10)
as H ≡ detE(M )
Z
pnon−inf(M )=M−1. (8) This effect tightens the M upper limit by 1 GeV.
H H H
2
[1] T. Junk, Combined LEP Higgs Searches, Talk presented
at theLEP Fest 2000, CERN, October 2000.
[2] http://www.physics.upenn.edu/˜erler/electroweak;
J. Erler, Global Fits to Electroweak Data Using GAPP,
e-print hep-ph/0005084, to appear in Physics at RUNII:
QCD and Weak Boson Physics.
[3] J. Erler and P. Langacker, Electroweak Model and Con-
straints on New Physics, p. 95 in Ref. [4].
[4] D.E. Groom et al., Eur. Phys. J. C15, 1 (2000).
[5] G. d’Agostini and G. Degrassi, Eur. Phys. J. C10, 663
(1999).
[6] T. Bayes, Phil. Trans. 53, 370 (1763), reprinted in Bio-
metrica 45, 296 (1958).
[7] For a comprehensive introduction and review of applied
statistics and data analysis see A. Gelman, J.B. Carlin,
H.S. Stern, and D.B. Rubin, Bayesian Data Analysis,
(Chapman & Hall, London,1995).
FIG. 2. Probability distribution function for the Higgs
boson mass. Theprobability isshown forbin sizes of 1GeV.
Includedareallavailabledirectandindirectdata. Theshaded
and unshaded regions each mark 50% probability.
I also include theory uncertainties from uncalculated
higher orders. This increases the upper limit by 5 GeV,
M 205 GeV (95% CL). (11)
H
≤
The entire probability distribution is shown in Fig. 2.
Taking the data at face value, there is (as expected)
a significant peak around M = 115 GeV, but more
H
than half of the probability is for Higgs boson masses
above the kinematic reach of LEP 2 (the median is at
M = 119 GeV). However, if one would double the in-
H
tegrated luminosity and assume that the results would
be similar to the present ones, one would find most of
the probability concentrated aroundthe peak. A similar
statement will apply to Run II ofthe Tevatronat a time
when about 3 to 5 fb−1 of data have been collected.
The described method is robust within the SM, but it
should be cautioned that M extracted from the preci-
H
sion data is strongly correlatedwith certain new physics
parameters. Likewise, the Higgs searches at LEP 2 de-
pend on the predictions of signalandbackgroundexpec-
tations which are strictly calculable only within a spec-
ified theory. This note focussed on the Standard Model
Higgs boson.
Acknowledgements:
This work was supported in part by the US Depart-
ment of Energy grant EY–76–02–3071.
3