THE “HYPER” BOLIC FUNCTIONS Antony Foster What are the PDF
Preview THE “HYPER” BOLIC FUNCTIONS Antony Foster What are the
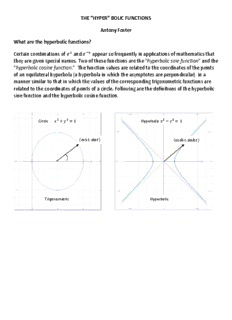
THE “HYPER” BOLIC FUNCTIONS Antony Foster What are the hyperbolic functions? Certain combinations of and appear so frequently in applications of mathematics that they are given special nam𝑥𝑥es. Two− o𝑥𝑥f these functions are the "hyperbolic sine function" and the 𝑒𝑒 𝑒𝑒 "hyperbolic cosine function.” The function values are related to the coordinates of the points of an equilateral hyperbola (a hyperbola in which the asymptotes are perpendicular) in a manner similar to that in which the values of the corresponding trigonometric functions are related to the coordinates of points of a circle. Following are the definitions of the hyperbolic sine function and the hyperbolic cosine function. Circle Hyperbola 2 2 2 2 𝑥𝑥 +𝑦𝑦 = 1 𝑥𝑥 −𝑦𝑦 = 1 (cos𝑡𝑡,sin𝑡𝑡) (cosh𝑡𝑡,sinh𝑡𝑡) Trigonometric Hyperbolic Definition: The hyperbolic sine function denoted by (pronounced “cinch”) is defined by 𝑠𝑠𝑠𝑠𝑠𝑠ℎ 𝑥𝑥 −𝑥𝑥 𝑒𝑒 − 𝑒𝑒 The domain and range is the set of all real numbers. sinh𝑥𝑥 = 2 sinh𝑥𝑥 Definition: The hyperbolic cosine function denoted by (rhymes with “gosh”) is defined by 𝑐𝑐𝑐𝑐𝑠𝑠ℎ 𝑥𝑥 −𝑥𝑥 𝑒𝑒 + 𝑒𝑒 The domain is the set of all real numbers and the range is the set of all real numbers in the cosh𝑥𝑥 = interval ∞ . 2 [1,+ ) cosh𝑥𝑥 Note that these functions are not periodic. The remaining four hyperbolic functions may be defined in terms of the hyperbolic sine and hyperbolic cosine functions. You should note that each satisfies a relation analogous to one satisfied by corresponding trigonometric functions. Definition: The hyperbolic tangent function, hyperbolic cotangent function, hyperbolic secant function, and hyperbolic cosecant function are defined, respectively, as follows: 𝑥𝑥 −𝑥𝑥 sinh𝑥𝑥 𝑒𝑒 − 𝑒𝑒 tanh𝑥𝑥 = = 𝑥𝑥 −𝑥𝑥 cosh𝑥𝑥 𝑒𝑒 + 𝑒𝑒 𝑥𝑥 −𝑥𝑥 1 𝑒𝑒 + 𝑒𝑒 coth𝑥𝑥 = = 𝑥𝑥 −𝑥𝑥 tanh𝑥𝑥 𝑒𝑒 − 𝑒𝑒 1 2 sech𝑥𝑥 = = 𝑥𝑥 −𝑥𝑥 cosh𝑥𝑥 𝑒𝑒 + 𝑒𝑒 1 2 csch𝑥𝑥 = = 𝑥𝑥 −𝑥𝑥 sinh𝑥𝑥 𝑒𝑒 − 𝑒𝑒 tanh𝑥𝑥 There are identities that are satisfied by the hyperbolic functions which are similar to those satisfied by the trigonometric functions. Four of the fundamental identities are given below. The other four fundamental identities are as follows: 1 tanh𝑥𝑥 = 2 co2th𝑥𝑥 cosh 𝑥𝑥 − sinh 𝑥𝑥 = 1 2 2 coth 𝑥𝑥 −2 1 = csch2𝑥𝑥 1 − tanh 𝑥𝑥 = sech 𝑥𝑥 Note the following identities 𝑥𝑥 −𝑥𝑥 𝑥𝑥 −𝑥𝑥 𝑥𝑥 𝑒𝑒 − 𝑒𝑒 𝑒𝑒 + 𝑒𝑒 𝑒𝑒 = + = sinh𝑥𝑥 + cosh𝑥𝑥 and ����2��� ����2��� 𝑂𝑂𝑂𝑂𝑂𝑂 𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 𝐸𝐸𝐸𝐸𝐸𝐸𝐸𝐸 𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 𝑥𝑥 −𝑥𝑥 𝑥𝑥 −𝑥𝑥 −𝑥𝑥 𝑒𝑒 + 𝑒𝑒 𝑒𝑒 − 𝑒𝑒 𝑒𝑒 = − = cosh𝑥𝑥 − sinh𝑥𝑥 From which it follows that we can d2erive hyperb2olic identities similar to the trigonometric identities 𝑥𝑥±𝑦𝑦 −(𝑥𝑥±𝑦𝑦) �𝑒𝑒 − 𝑒𝑒 � sinh(𝑥𝑥 ± 𝑦𝑦) = = sinh𝑥𝑥cosh𝑦𝑦 ± sinh𝑦𝑦cosh𝑥𝑥 2 𝑥𝑥±𝑦𝑦 −(𝑥𝑥±𝑦𝑦) 𝑒𝑒 + 𝑒𝑒 cosh(𝑥𝑥 ± 𝑦𝑦) = = cosh𝑥𝑥cosh𝑦𝑦 ± sinh𝑥𝑥sinh𝑦𝑦 2 𝑥𝑥±𝑦𝑦 −(𝑥𝑥±𝑦𝑦) 𝑒𝑒 − 𝑒𝑒 tanh𝑥𝑥 ± tanh𝑦𝑦 tanh(𝑥𝑥 ± 𝑦𝑦) = 𝑥𝑥±𝑦𝑦 −(𝑥𝑥±𝑦𝑦) = 𝑒𝑒 + 𝑒𝑒 1 ∓ tanh𝑥𝑥tanh𝑦𝑦 sinh2𝑥𝑥 = 2sinh𝑥𝑥cosh𝑥𝑥 2 2 cosh 𝑥𝑥 + sinh 𝑥𝑥 2 � cosh2𝑥𝑥 = � 2sinh 𝑥𝑥 + 1 2 2cosh 𝑥𝑥 − 1 2tanh𝑥𝑥 tanh2𝑥𝑥 = 2 1 − tanh 𝑥𝑥 𝑥𝑥 cosh𝑥𝑥 − 1 sinh = ±� 2 2 𝑥𝑥 cosh𝑥𝑥 + 1 cosh = � 2 2 DERIVATIVE OF THE HYPERBOLIC FUNCTIONS The formulas for the derivatives of the hyperbolic sine and hyperbolic cosine functions may be obtained by applying the definitions and differentiating the resulting expressions involving exponential functions. For example, 𝑥𝑥 −𝑥𝑥 𝑥𝑥 −𝑥𝑥 𝑑𝑑 𝑑𝑑 𝑒𝑒 − 𝑒𝑒 𝑒𝑒 + 𝑒𝑒 (sinh𝑥𝑥) = � � = = cosh𝑥𝑥 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 2 2 𝑥𝑥 −𝑥𝑥 𝑥𝑥 −𝑥𝑥 𝑑𝑑 𝑑𝑑 𝑒𝑒 + 𝑒𝑒 𝑒𝑒 − 𝑒𝑒 (cosh𝑥𝑥) = � � = = sinh𝑥𝑥 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 2 2 2 2 𝑑𝑑 𝑑𝑑 sinh𝑥𝑥 cosh 𝑥𝑥 − sinh 𝑥𝑥 1 2 (tanh𝑥𝑥) = � � = 2 = 2 = sech 𝑥𝑥 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 cosh𝑥𝑥 cosh 𝑥𝑥 cosh 𝑥𝑥 𝑑𝑑 𝑑𝑑 1 2 (csch𝑥𝑥) = � � = −(cosh𝑥𝑥)/(sinh 𝑥𝑥) = −csc𝑥𝑥coth𝑥𝑥 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 sinh𝑥𝑥 𝑑𝑑 𝑑𝑑 1 (sech𝑥𝑥) = � � = −sech𝑥𝑥tanh𝑥𝑥 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 cosh𝑥𝑥 𝑑𝑑 𝑑𝑑 1 2 2 2 (coth𝑥𝑥) = � � = −(sech 𝑥𝑥)/(tanh 𝑥𝑥) = −csch 𝑥𝑥 𝑑𝑑 𝑥𝑥 𝑑𝑑𝑥𝑥 tanh𝑥𝑥 You should notice that the formulas for the derivatives of the hyperbolic sine, cosine, and tangent all have a plus sign, whereas the formulas for the derivatives of the hyperbolic cotangent, secant, and cosecant all have a minus sign. Otherwise, the formulas are similar to the corresponding formulas for the derivatives of the trigonometric functions. Example 1: Find if 2 𝑑𝑑𝑦𝑦/𝑑𝑑𝑥𝑥 𝑦𝑦 = tanh (1 − 𝑥𝑥 ) Solution: 𝑑𝑑𝑦𝑦 𝑑𝑑 2 2 2 𝑑𝑑 2 2 2 = (tanh(1 − 𝑥𝑥 )) = sech (1 − 𝑥𝑥 ) ⋅ (1 − 𝑥𝑥 ) = −2𝑥𝑥sech (1 − 𝑥𝑥 ) 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 𝑑𝑑𝑥𝑥 Example 2: Find if 2 𝑑𝑑𝑦𝑦/𝑑𝑑𝑥𝑥 𝑦𝑦 = ln(sinh𝑥𝑥 ) Solution 2 𝑑𝑑 2 1 𝑑𝑑 2 2𝑥𝑥cosh𝑥𝑥 2 (ln(sinh𝑥𝑥 )) = 2 ⋅ (sinh𝑥𝑥 ) = 2 = 2𝑥𝑥tanh𝑥𝑥 𝑑𝑑𝑥𝑥 sinh𝑥𝑥 𝑑𝑑𝑥𝑥 sinh𝑥𝑥 INTEGRALS OF THE HYPERBOLIC FUNCTIONS The six derivative formulas above gives rise to six integral formulas below ∫ sinh𝑥𝑥𝑑𝑑𝑥𝑥 = cosh𝑥𝑥 + 𝐶𝐶 ∫ cosh𝑥𝑥 𝑑𝑑𝑥𝑥 = sinh𝑥𝑥 + 𝐶𝐶 2 ∫ sech 𝑥𝑥 𝑑𝑑𝑥𝑥 = tanh𝑥𝑥 + 𝐶𝐶 ∫ csch𝑥𝑥coth𝑥𝑥 𝑑𝑑𝑥𝑥 = −csch𝑥𝑥 + 𝐶𝐶 ∫ sech𝑥𝑥tanh𝑥𝑥 𝑑𝑑𝑥𝑥 = −sech𝑥𝑥 + 𝐶𝐶 2 ∫ csch 𝑥𝑥 𝑑𝑑𝑥𝑥 = −coth𝑥𝑥 + 𝐶𝐶 Example 3. Evaluate the indefinite integral Solution 3 2 ∫ sinh 𝑥𝑥coth 𝑥𝑥 𝑑𝑑𝑥𝑥 2 2 2 2 ∫ sinh 𝑥𝑥cosh 𝑥𝑥𝑠𝑠𝑠𝑠𝑠𝑠ℎ𝑥𝑥 𝑑𝑑𝑥𝑥 = ∫(cosh 𝑥𝑥 − 1)cosh 𝑥𝑥sinh𝑥𝑥 𝑑𝑑𝑥𝑥 4 2 = ∫ (cosh 𝑥𝑥 − cosh 𝑥𝑥)sinh𝑥𝑥 𝑑𝑑𝑥𝑥 4 2 = ∫ cosh 𝑥𝑥sinh𝑥𝑥 𝑑𝑑𝑥𝑥 − ∫ cosh sinh𝑥𝑥 𝑑𝑑𝑥𝑥 1 5 1 3 = cosh 𝑥𝑥 − cosh 𝑥𝑥 + 𝐶𝐶 Example 4. Evaluate the indefinite i5ntegral 3 Solution: 4 ∫ sech 𝑥𝑥 𝑑𝑑𝑥𝑥 4 2 2 2 2 ∫ sech 𝑥𝑥 𝑑𝑑𝑥𝑥 = ∫(sech 𝑥𝑥) 𝑑𝑑𝑥𝑥 = ∫ sech 𝑥𝑥 sech 𝑥𝑥 𝑑𝑑𝑥𝑥 2 2 = ∫(1 − tanh 𝑥𝑥)sech 𝑥𝑥 𝑑𝑑𝑥𝑥 2 2 2 = ∫ sech 𝑥𝑥 𝑑𝑑𝑥𝑥 − ∫ tanh 𝑥𝑥sech 𝑥𝑥 𝑑𝑑𝑥𝑥 1 3 = tanh𝑥𝑥 − tanh 𝑥𝑥 + 𝐶𝐶 3 A catenary is the curve formed by a homogeneous flexible cable hanging from two points under its own weight. If the lowest point of the catenary is the point , it can be shown that an equation of it is (0,𝑎𝑎) 𝑥𝑥 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) = 𝑎𝑎cosh , 𝑎𝑎 > 0 𝑎𝑎 Post Post Catenary Example 5 Find the length of the arc of the catenary have equation 𝑥𝑥 from the point to a point where 𝑦𝑦 = 𝑎𝑎cosh�𝑎𝑎�,𝑎𝑎 > 0 (0,𝑎𝑎) (𝑥𝑥1,𝑦𝑦1) 𝑥𝑥1 > 0. Solution: and so 𝑑𝑑𝑦𝑦 𝑑𝑑 𝑥𝑥 𝑥𝑥 1 𝑥𝑥 𝑑𝑑𝑥𝑥 = 𝑑𝑑𝑥𝑥 �𝑎𝑎cosh�𝑎𝑎�� = 𝑎𝑎sinh�𝑎𝑎� ⋅ 𝑎𝑎 = sinh�𝑎𝑎� 2 𝑑𝑑𝑦𝑦 2 𝑥𝑥 𝑥𝑥 Therefore, the arc length� is1 + � � = �1 + sinh � � = cosh� � 𝑑𝑑𝑥𝑥 𝑎𝑎 𝑎𝑎 𝑥𝑥1 2 𝑥𝑥1 𝑥𝑥1 𝑑𝑑𝑦𝑦 𝑥𝑥 𝑥𝑥 𝑥𝑥1 � � 1 + � � 𝑑𝑑𝑥𝑥 = � cosh� � 𝑑𝑑𝑥𝑥 = �𝑎𝑎sinh� �� = 𝑎𝑎sinh� � − 𝑎𝑎sinh0 0 𝑑𝑑𝑥𝑥 0 𝑎𝑎 𝑎𝑎 0 𝑎𝑎 𝑥𝑥1 = 𝑎𝑎sinh� � 𝑎𝑎 THE INVERSE OF THE HYPERBOLIC FUNCTIONS From the graph of the hyperbolic sine function (drawn above), we see that any horizontal line intersects the graph in one and only one point; therefore, to each number in the range of the function there corresponds one and only one number in the domain. The hyperbolic sine function is continuous and increasing on its domain, and so the hyperbolic sine function has an inverse function. Definition. The inverse hyperbolic sine function, denoted by , is defined as follows: −1 sinh 𝑥𝑥 −1 𝑦𝑦 = sinh 𝑥𝑥 ⇔ 𝑥𝑥 = sinh𝑦𝑦 −1 sinh 𝑥𝑥 A sketch of the graph of is show above and its domain and range is the set of all real numbers. −1 𝑦𝑦 = sinh 𝑥𝑥 It follows from earlier discussions about inverse functions that −1 −1 −1 −1 f(f (x)) = sinh(sinh 𝑥𝑥) = 𝑥𝑥 and 𝑓𝑓 �𝑓𝑓(𝑦𝑦)� = sinh (sinh𝑦𝑦) = 𝑦𝑦. From the graph of the hyperbolic cosine, we notice that any horizontal line , where intersects the graph in two points. Therefore, for each number greater than in the 𝑦𝑦 = 𝑘𝑘 range of this function, there corresponds two numbers in the domain. So the hyperbolic cosine 𝑘𝑘 > 1, 1 function does not have an inverse function. However, we define a function as follows: 𝐹𝐹 𝐹𝐹(𝑥𝑥) = cosh𝑥𝑥, for 𝑥𝑥 ≥ 0 The domain of is the interval , and the range is the interval A sketch of the graph of F is shown above. The function F is continuous and increasing on its entire domain, 𝐹𝐹 [0,+∞) [1,+∞). and so, F has an inverse function, which we call the "inverse hyperbolic cosine function.” Definition: The inverse hyperbolic cosine function, denoted by , is defined as follows: −1 cosh 𝑥𝑥 −1 𝑦𝑦 = cosh 𝑥𝑥 ⇔ 𝑥𝑥 = cosh𝑦𝑦 and 𝑦𝑦 ≥ 0. −1 cosh 𝑥𝑥 A sketch of the graph of the inverse hyperbolic cosine function is shown above. The domain of this function is the interval and the range is the interval . We conclude That [1,+∞), [0,+∞) −1 −1 𝑐𝑐𝑐𝑐𝑠𝑠ℎ(cosh 𝑥𝑥 ) = 𝑥𝑥 if 𝑥𝑥 ≥ 1 and cosh (cosh𝑦𝑦) = 𝑦𝑦 and y≥0 As with the hyperbolic sine function, a horizontal line intersects each of the graphs of the hyperbolic tangent function, the hyperbolic cotangent function, and the hyperbolic cosecant function at one and only one point. For the hyperbolic tangent function, this may be seen below. Each of the above three functions is continuous and monotonic on its domain; hence, each has an inverse function. tanh𝑥𝑥 The inverse hyperbolic tangent function, the inverse hyperbolic cotangent function, and the inverse hyperbolic cosecant function, denoted respectively by , , and , are defined as follows: −1 −1 tanh 𝑥𝑥 coth 𝑥𝑥 −1 csch 𝑥𝑥 −1 𝑦𝑦 = tanh 𝑥𝑥 ⇔ 𝑥𝑥 = tanh𝑦𝑦 −1 𝑦𝑦 = coth 𝑥𝑥 ⇔ 𝑥𝑥 = coth𝑦𝑦 −1 𝑦𝑦 = csch 𝑥𝑥 ⇔ 𝑥𝑥 = csch𝑦𝑦
Description:The list of books you might like
