The Faintest X-ray Sources from z=0-8

0.63 MB·

by  L. L. Cowie

DraftversionJanuary17,2012
PreprinttypesetusingLATEXstyleemulateapj
THE FAINTEST X-RAY SOURCES FROM Z =0−81,2,3
L. L. Cowie,4 A. J. Barger,4,5,6 G. Hasinger4
In press at The Astrophysical Journal
ABSTRACT
We use the new 4 Ms exposure of the CDF-S field obtained with the Chandra X-ray satellite to
2
investigatethepropertiesofthefaintestX-raysourcesoverawiderangeofredshifts. Weuseanoptimized
1
averaging procedure to investigate the weighted mean X-ray fluxes of optically selected sources in the
0
2 CDF-Sovertheredshiftrangez =0−8anddownto0.5−2keVfluxesaslowas5×10−19 ergcm−2 s−1.
None of the samples of sources at high redshifts (z > 5) show any significant flux, and at z = 6.5 we
n placeanupperlimitonthe X-rayluminosityof4×1041 ergs−1 inthe rest-frame3.75−15keVbandfor
a
J the sample of Bouwens et al. (2006). This is consistent with any X-ray production in the galaxies being
solely due to star formation. At lower redshifts we find significant weighted mean X-ray fluxes in many
3
samplesofsourcesoverthe redshiftrangez =0−4. Weuse theseto arguethat(1)the relationbetween
1
star formationand X-ray productionremains invariantoverthis redshift range,(2) X-ray sources below

] the direct detection threshold in the CDF-S are primarily star-forming,and (3) there is full consistency
O between UV and X-ray estimations of the star formation history.
C Subject headings: cosmology: observations— galaxies: distances and redshifts — galaxies: evolution—
. galaxies: starburst — galaxies: active
h
p
1. INTRODUCTION verse, it does not rule out the possibility that substantial
-
o accretion onto supermassive black holes is occurring be-
Wewouldliketobeabletodeterminedirectlyhowmuch
r hind veils of obscuring material. The only way to deter-
t growthoccursinsupermassiveblackholesintheearlyuni-
s mine this is by probing the faintest X-ray fluxes. Thus,
verse. Unfortunately, however, only the most luminous
a the continued deepening of the deepest X-ray images of
[ quasarsatz >6haveeverbeendetectedindividually(e.g.,
Fan et al. 2006;Willott et al. 2010;Mortlock et al. 2011), the sky is essentialfor studying this important issue. The
2 latest of these deepenings is the now nearly 4 Ms of expo-
and these sources are so massive that their evolutionary
v sure on the Chandra Deep Field-South (CDF-S; Giaconni
histories are far from typical.
6 etal.2002;Alexanderetal.2003,hereafterA03;Luoetal.
We wouldalsolike toknowthe relativecontributionsof
2 2008;Xue et al. 2011,hereafter X11). The 4 Ms exposure
the galaxyandactivegalacticnucleus (AGN) populations
3 is deep enough to detect all sources above a luminosity of
3 to the UV and X-ray ionizing radiation in the early uni- ∼ 5×1042 erg s−1 in the rest-frame 3.5−14 keV band
. verse. Estimates from optical data were that AGNs could
0 at z = 6. Thus, almost all luminous AGNs, even at very
not account for the required UV ionizing flux at z > 3
1 high redshifts, will be included in the catalog of directly
(e.g., Bolton et al. 2005; Meiksin 2005). It is now recog-
1 detected sources. However, only one source with a red-
nized that complete samples of AGNs—or at least those
1 shift greaterthan z =5 has been spectroscopicallyidenti-
: which are not Compton thick—are most easily obtained
v fied(Bargeretal.2003)inthe Chandra Deep Field-North
with X-ray observations. Direct searches for high-redshift
i (CDF-N; Brandt et al. 2001; A03) and CDF-S fields.
X (z = 3.5− 6.5) AGNs carried out using combined deep
Faintersourcesarelikelytobedominatedbystarforma-
Chandra X-ray samples and optical imaging data (e.g.,
r tion,low-luminosityAGNs(LLAGNs), orhighlyobscured
a Barger et al. 2003; Fontanot et al. 2007) also found that
AGNs. Suchsourcesshouldhavestrongbreaksintherest-
the ionizationfromAGNs wasinsufficientto maintainthe
frame UV owing to the Lyα forest of the intergalactic gas
observed ionization of the intergalactic medium at high
or to the intrinsic Lyman continuum break and should
redshifts. Thisresultwasconclusivelyestablishedatz >3
be included in optical or near-infrared dropout samples
by Cowie et al. (2009) by measuring the contribution of
identified from the break properties. We can attempt to
AGNs to the ionizing flux as a function of redshift using
measure the properties of these fainter sources through
X-ray, optical, and UV observations.
averaging (sometimes referred to as “stacking”) analyses
However, even if the space-density of high-redshift, un-
of optically or near-infraredselected galaxy samples (e.g.,
obscuredAGNs isnotsufficientlyhightoreionizethe uni-
1Based in part on data obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the/ the California
Institute ofTechnology, theUniversityofCalifornia,andNASAand wasmade possiblebythe generous financial supportofthe W. M.Keck
Foundation.
2Based in part on observations taken by the CANDELS Multi-Cycle Treasury Program with the NASA/ESA HST, which is operated by
theAssociationofUniversitiesforResearchinAstronomy,Inc.,underNASAcontractNAS5-26555.
3BasedinpartondataobtainedfromtheMultimissionArchiveattheSpaceTelescopeScienceInstitute(MAST).STScIisoperatedbythe
AssociationofUniversitiesforResearchinAstronomy,Inc.,underNASAcontract NAS5-26555.
4Institute forAstronomy,UniversityofHawaii,2680WoodlawnDrive,Honolulu,HI96822.
5DepartmentofAstronomy,UniversityofWisconsin-Madison,475NorthCharterStreet,Madison,WI53706.
6DepartmentofPhysicsandAstronomy,UniversityofHawaii,2505CorreaRoad,Honolulu,HI96822.
1
2
Brandt et al. 2001; Nandra et al. 2002; Reddy & Steidel estimations of the star formation history.
2004; Lehmer et al. 2005; Worsley et al. 2006; Hickox & We use a standard H = 70 km s−1 Mpc−1, Ω = 0.3,
0
Markevitch 2006, 2007; Treister et al. 2011). This is of Ω=0.7 cosmologythroughout. All magnitudes are in the
particular interest for the highest redshift samples, where AB magnitude system.
wemaybeprobingsupermassiveblackholesattimesvery
close to their formation. However, it also allows us to ex- 2. X-RAYDATA
amine the X-rayproperties ofstar-forminggalaxiesovera X11 presented the X-ray images from the 3.872 Ms
wide range in redshifts (out to beyond z = 4) and to test total exposure of the CDF-S, which covers an area of
whetherthe propertiesofthesegalaxieschangewithtime. 464.5arcmin2. TheyprovidedamainChandra sourcecat-
Treister et al. (2011; hereafter T11) used the CDF-N alogcontaining740X-raysourcesdetectedwithWAVDE-
andCDF-SdatatoperformsensitiveX-raystackinganal- TECT at a false-positive probability threshold of 10−5 in
ysesonz >6galaxycandidatesthatcouldnotbedetected at least one of three X-ray bands: full (0.5 − 8 keV),
individually to look for detectable X-ray signal from the soft (0.5 − 2 keV), and hard (2 − 8 keV). The catalog
population as a whole. The high-redshift samples they also satisfies a binomial-probability source-selection cri-
used (z ∼ 6 from Bouwens et al. 2006, hereafter Bo06, terion of P < 0.004, which means that the probability
and z ∼ 7 and z ∼ 8 from Bouwens et al. 2011, here- that the sources not are real is less than 0.004. The
after Bo11) were selected with the drop-out technique us- on-axis flux limits are ≈ 3.2 × 10−17, 9.1 × 10−18, and
ing Hubble Space Telescope (HST) ACS and WFC3 data. 5.5×10−17ergcm−2 s−1 forthefull,soft,andhardbands,
For the z ∼ 6 Bo06 sample, T11 found significant detec- respectively.
tions (≥ 5σ) in both the observed soft (0.5−2 keV) and The CDF-S is now almost twice as deep as the CDF-N
theobservedhard(2−8keV)bands. Thestackedhard-to- field,whichistheonlyotherextremelydeepChandra field.
soft X-ray flux ratio that they found was a relatively high For most of our analysis we will therefore concentrate on
factor of ∼9, which they said could only be explained by the CDF-S alone, but in some cases we will also include
very high levels of obscuration. Moreover, since the ratio similarly selected samples from the CDF-N, where these
was a ratio of the stacks,they inferredthat there must be can provide an increase in the sensitivity. For the CDF-N
very few sources with significantly lower levels of obscu- we use the images and corresponding source catalog from
ration. This led them to the conclusion that black holes A03,whichcontains503sourcesselectedinthesamethree
grow significantly at early times but are heavily buried in X-ray bands described above.
gas and dust. X11 shifted the optical positions in deep R-band
These results are rather surprising. Galaxies selected imaging data—which were already matched to the HST
by the drop-out technique are generally classic starburst ACS Great Observatories Origins Deep Survey-South
galaxies;i.e., they are small, blue, and compact with high (GOODS-S; Giavalisco et al. 2004) images—by 0′.′175 in
surface brightnesses (e.g., Stanway et al. 2004). Mean- right ascension and −0′.′284 in declination in order to
while, the masses of local supermassive black holes are match them to the radio positions of sources in the Very
generallycorrelatedwiththebulgeluminositiesofthehost Large Array (VLA) 1.4 GHz radio catalog (5σ) of Miller
galaxies(e.g.,Ferrarese&Merritt2000;Kormendy&Geb- etal.(2008)andN.A.Milleretal.(2011),inpreparation.
hardt 2001; Gebhardt et al. 2000; Tremaine et al. 2002). They then matched the X-ray centroid positions to the
At z ∼ 3, this would be akin to finding AGNs in Lyman opticalsourcesdetected in the R-bandimage to put them
Break Galaxies (LBGs), which is not very common (e.g., on a common astrometric frame. In this paper, we moved
Steideletal.2004). Moreover,iftherewerealotofgasand X11’s source positions back to the GOODS-S ACS frame
dust present to obscure the central black hole (T11 argue by shifting them by −0′.′175 in right ascension and 0′.′284
thatthesourcesmustbenearlyCompton-thickalongmost in declination. This allows us to work with the astromet-
directions), then one might expect the dust to also affect ricpositionsoftheopticalsourcesandspectraldatainthe
the properties of the host galaxy, unless it were somehow GOODS-S samples.
confined to the region around the AGN itself. In Figure 1 we show the X-ray image of the CDF-S.
Indeed, Fiore et al. (2011) conducted an independent, With small circles we show the positions of all of the X-
non-optimized stacking analysis using the Bo06 sample in ray sources from X11. With larger circles we show the
the CDF-S and did not confirm the T11 results. More re- positions of the X-ray sources that also have deep near-
cently, Willott (2011)providedanindependent critique of infrared(NIR) coveragefromHST WFC3 imaging (Early
T11thatparallelssomeoftheresultsofthepresentpaper. Release Science or ERS, Windhorst et al. 2011; Cosmic
HerewearguethattheT11resultisaconsequenceofan Assembly Near-Infrared Deep Extragalactic Legacy Sur-
incorrect background subtraction procedure. In our anal- vey or CANDELS, Grogin et al. 2011 and Koekemoer et
ysis we find a 2σ upper limit on the X-ray luminosity at al. 2011). Given the X-ray positional uncertainties, we
z = 6.5 of 4×1041 erg s−1, which is consistent with any identified an X-ray source with a NIR counterpart if an
X-ray production in the galaxies being solely due to star F160W band counterpart brighter than F160W∼ 25 (5σ)
formation. waswithin2′′ oftheX-rayposition. Ifmorethanonesuch
At lower redshifts we find significant weighted mean X- NIR counterpart was within the search radius, then we
ray fluxes in many samples of sources over the redshift identifiedtheX-raysourcewiththenearestNIRneighbor.
range z = 0−4. We use these to argue that (1) the rela- As pointed out in X11 (see also A. J. Barger et al. 2011,
tionbetweenstarformationandX-rayproductionremains in preparation), nearly all of the X-ray sources have NIR
invariantover this redshift range,(2) X-ray sourcesbelow counterparts. Finally, we mark with a rectangle the part
the direct detection threshold are primarily star-forming, of the GOODS-S region that was uniformly covered with
and (3) there is full consistency between UV and X-ray ACS. The X-ray sensitivity degrades rapidly at large off-
Cowie, Barger,& Hasinger 3
Fig. 1.—CDF-S4Msfull-bandimageoverlaidwithacircleshowinganoff-axisradiusof6′andarectangleshowingtheHST ACSuniformly
coveredregionoftheGOODS-S(Giavaliscoetal.2004). ThesmallcirclesshowthepositionsoftheX-raysourcesintheX11CDF-Scatalog,
and thelargercirclesshow theX-raysources withNIRcoverage fromthe ERS(Windhorst etal.2011) andCANDELS(Grogin etal.2011;
Koekemoer et al. 2011) observations using the F125W and F160W filters on HST WFC3. We refer to the area within both the 6′ radius
circleandtheuniformlycoveredregionoftheGOODS-Sasourcoreregion.
axis radiias the point spread function (PSF) of the X-ray etal.(2001),Bunkeretal.(2003),Dickinsonetal.(2004),
imageincreases,sowerestrictouranalysistosourceslying Stanwayetal.(2004),Strolgeretal.(2004),Szokolyetal.
withinanoff-axisradiusof6′(verylargecircle). Theover- (2004),vanderWeletal.(2004),Dohertyetal.(2005),Le
lap of the 6′ regionwith the uniformly coveredGOODS-S F`evreetal.(2005),Mignolietal.(2005),Ravikumaretal.
regionis 101arcmin2. This regioncontains 360of the 740 (2007), and Vanzella et al. (2008). We added to this cat-
X-ray sources in X11 and 19,294 of the 33,955 optically alog 144 new redshifts for previously unidentified sources
selected sources given in the v2 catalog of the ACS obser- thatwemeasuredwithDEIMOSintheFallof2010,aswell
vations of the GOODS-S. In this paper we shall refer to some additional redshifts obtained by S. Koposov et al.
this overlap region in both fields as our core region. (unpublished) that were presented in Taylor et al. (2009).
In our compilation we only included sources with secure
3. TARGETSAMPLESOVERTHEZ =0−8REDSHIFT redshifts. In the case of the VIMOS-VLT Deep Survey or
RANGE VVDS (Le F`evre et al. 2005), we only included sources
We measured the weighted mean X-ray counts s−1 in classified as 100% secure. We included a small number of
three types of selected galaxy samples. First, we used redshifts from papers that did not give a quality flag, but
galaxies with secure spectroscopic redshifts. This is a rel- in these cases the spectral identifications appeared robust
ativelysmallsample,andthesourcesarebrightintherest- based on the material presented in the papers.
frame optical. Thus, if more optically-luminous galaxies In our final compilation, we have secure redshifts for
are X-ray brighter (e.g., Lehmer et al. 2005), then this 1792 galaxies and 158 stars in the full GOODS-S field.
samplemaybeexpectedtoproducehigherweightedmean In Figure 2(a) we plot the spectroscopic redshifts versus
X-ray counts s−1. Second, we used a photometric redshift the F850LP magnitudes for the final compilation (black
sampletoprobefaintergalaxies. Finally,weuseddropout small squares). 1158 of the galaxies with secure redshifts
selectedsamplestoprovideascompleteaselectionaspos- lie in the core region. Using insecure redshifts would add
sible in a given redshift range. a comparablenumber of additionalredshifts, but many of
these are clearly problematic based on our inspections of
3.1. Secure Spectroscopic Redshift Sample thespectraoronourcomparisonsoftheredshiftsgivenin
the different catalogs, so we prefer to work only with the
FortheGOODS-S,westartedwiththeEuropeanSouth-
secure redshifts.
ern Observatory (ESO) master redshift catalog compiled
FortheGOODS-N,weusedthecatalogsofBargeretal.
by A. Rettura in 2004 and subsequently updated by
(2008)updatedwithasyetunpublishedDEIMOSredshifts
Popesso et al. (2009)and Balestra et al. (2010). This cat-
obtainedbyusandsomeadditionalredshiftsfromCooper
alogincludes redshifts fromCristianietal.(2000),Croom
4
et al. (2011). The GOODS-N sample has secure redshifts are a fair number of outliers: about 4% of sources lie at
for2987galaxiesand199stars. Theslightlylargersample (z−z )/(1+z)>0.2. Muchofthisseemstobeassociated
p
in the GOODS-N as comparedto the GOODS-S compen- withthez =2−3redshiftrange. Athigherredshiftsthere
satesfortheshallowerexposureintheCDF-N,andweuse are few problems, presumably because the identifications
both samples in computing the weighted mean fluxes. aremoresecureduetothebreaks. InFigure2(b)weshow
the photometric redshifts versus the F850LP magnitudes
fortheGrazianetal.(2006)sample(blacksmallsquares).
This sample contains 10,071 galaxies in our core region.
3.3. Dropout Samples
We used Beckwith et al. (2006, hereafter Beck06)’s list
ofb(1335),v(328),andi(105)dropoutsintheGOODS-S
and Hubble Ultra Deep Field (HUDF). Bo06 compiled an
alternative list of 522 i dropouts in these fields plus the
GOODS-N. The Beck06 i dropout sample overlaps with
the Bo06 sample but contains some sources that are not
in Bo06 and vice versa. We will consider both of these
samples separately in our subsequent analysis.
We show the sources in these dropout selected samples
in the redshift-magnitude plots of Figure 2 (colored sym-
bols). Allofthe spectroscopicallyidentifiedsourcesfallat
theredshiftsexpectedfromthedropoutselection. Thereis
asmallamountofinconsistencybetweenthedropoutsand
the photometric redshifts, as can be seen in Figure 2(b),
where a number of the dropouts lie at low photometric
redshifts. The inconsistent fraction is 68 out of 631 ob-
jects with photometric redshifts in the b dropout sample,
33 out of 161 in the v dropout sample, and 6 out of 39 in
the i dropout sample. The median photometric redshifts
(which we will use for later plots) are z = 3.74 for the b
dropouts, z =4.78 for the v dropouts, and =5.84 for the
idropouts(wherethelattercontainsboththeBeck06and
Bo06 samples).
Higher redshift (z ∼ 7 − 8) sources fall out of the
GOODS-SF850LPselectedsample. Hereweuse thesam-
pleofBo11. AlthoughMcLureetal.(2011)criticizedsome
of the Bo11 sources (which they consider to be lower red-
shift interlopers) and gave their own robust list, we use
the Bo11samples here because they are deeper. However,
we note that we do not detect any significant mean X-ray
flux in either sample and that the error limits are similar
regardless of the choice of sample.
Fig. 2.— (a) Secure spectroscopic redshift vs. F850LP magni- 4. OPTIMIZEDAVERAGINGPROCEDURE
tude for all the sources with secure spectroscopic redshifts in the
full GOODS-S (black small squares; see text for references). X- AfullyoptimallyweighteddeterminationofthemeanX-
ray sources are marked with a black enclosing square. The lower
rayflux in a sample fromthe Chandra data wouldinvolve
blue histogram (right-hand vertical scale) shows the fraction of
sources that have not been identified as a function of magnitude. usingvariableellipticalaperturesthataredynamicallyad-
(b) Same for the sources with photometric redshifts from Grazian justedtomatchthelocalPSFsandbackground. However,
etal.(2006). Thecoloredsymbolsshowtheb(blue),v(green),and withoptimalweightings,mostofthesignal—evenforaset
i(red)dropoutsfromBeck06(plusBo06fortheidropoutsample)
ofsourcesthatisuniformlydistributedoverthefullChan-
that have (a) spectroscopic redshifts or (b) photometric redshifts.
ThemoreX-rayluminousbroad-lineAGNsarenotselectedbythe dra field—arisesatrelativelysmalloff-axisradii(lessthan
dropouttechniques. 6′), where we may include most of the counts within the
PSFwithamoderatelysizedcircularaperture(e.g.,Allen
et al. 2004). Even at these small off-axis angles the opti-
3.2. Photometric Redshift Sample
malweightingofthe Chandra datainvolvesseveralissues,
Forourphotometricredshiftsample,werestrictedtothe most particularly which aperture to choose and how far
deeperCDF-SdataandusedtheGOODS-MUSICcatalog outinoff-axisangleto include sources(e.g., Lehmeret al.
of Grazian et al. (2006). (Dahlen et al. 2010 report on an 2005; Hickox & Markevitch 2006, 2007; T11).
alternate photometric redshift computation based on up- For faint sources, the noise level is dominated by the
dateddata, butthe actualcataloghas yetto be released.) background. We may write the S/N in an aperture of ra-
The Grazian et al. catalog gives photometric redshifts for diusr asproportionalto f(r,θ)/(b0.5×r), wheref(r,θ)is
13,820sourcesinthefullGOODS-Sfield. Theyreproduce thefractionofthecountsfromthesourcecontainedwithin
the secure spectroscopicredshifts quite well, thoughthere the aperture at off-axis radius θ (often referred to as the
Cowie, Barger,& Hasinger 5
enclosedenergyfraction),andbisthebackgroundperunit general,thenumberofbackgroundcountsintheaperture,
solid angle (see also T11). We show this quantity for the B, is high enough to justify the Gaussian approximation.
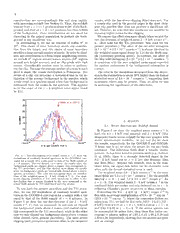
2−8keVbandinFigure3asafunctionofθ(blacksolid: 0′ Foragivensampleweformtheoptimallyweightedmean
or on-axis; red: 1.5′; blue: 3′; green: 5′; black dashed: 7′) X-raycounts s−1, L,and the correspondingerror,E . To
L
and r, assuming b is roughly constant within the region. do this, we first exclude all sources with a known X-ray
As T11 point out, the optimal r to maximize the S/N in- sourcewithin6′′orabright(0.5−8keVcountsabove1000)
creases with increasing θ, rising from r = 0.4′′ at θ = 0′ X-ray source within 13′′ in the existing catalogs (X11 for
(black solid) to approximately r = 5′′ at θ = 7′ (black the CDF-S and A03 for the CDF-N) to remove any con-
dashed). However, as can also be seen from Figure 3, the tamination from these sources. These two values (6′′ and
dependence on r at larger θ is very soft, so choosing a 13′′) correspond to the 90% and 95% enclosed light radii,
smaller aperture radiushas little effect onthe S/N.More- respectively, at an energy of 5 keV and an off-axis radius
over,using a smaller apertureradius has the advantageof of 6′. This ensures that the contribution from the ex-
minimizing contamination by neighboring sources. tended wings of the known sources is less than about a
A very small aperture is optimal close to on-axis, but count in any aperture, even for the hard band. When av-
the use of such a small aperture places stress on the as- eraged over the ensembles, this level of contamination is
trometry (see T11). We have therefore chosen to use a negligible. Our contamination radii are smaller than the
constant r = 0.75′′ aperture within an off-axis angle of values adopted by Hickox & Markevitch (2006, 2007) or
θ = 3′ and a constant r = 1.25′′ aperture at larger θ. by T11, but tests with random samples show that there
This roughly brackets the optimal radius for θ = 3′ (see is little sensitivity to increasing them, and choosing the
blue curve in Figure 3 for the 2−8 keV band), namely smallest possible contamination radii minimizes the num-
r = 0.9′′ in the 0.5− 2 keV band and r = 1.2′′ in the ber of sources excluded by this step. The adopted proce-
2−8 keV band. The noise in typical samples computed durereducesthecoreareafrom101arcmin2to86arcmin2.
with this procedure only differs from that computed with We form the optimally weighted mean X-ray counts s−1,
a fully optimizedapertureasa functionofradiusby afew L = Σ(C/E2)/Σ(1/E2), by summing over the remain-
percent. ing sources in the sample. The corresponding error is
We include sources out to θ =6′, which, in conjunction E =(1/Σ(1/E2))0.5.
L
with the samples lying within the well covered areas of Thefinalissueishowtocomputethebackgroundcounts
the GOODSfields,is ourdefinitionofthe coreregion. We per unit solid angle, b. There are two possible approaches
stress that the results are quite insensitive to the choice to this. One can compute a local background for each
of the maximum θ, because the high off-axis sources have source using either a surrounding annulus (T11) or a
low S/N in an optimally weighted mean. Decreasing the wavelet approach (Hickox & Markevitch 2006, 2007), or
off-axis angle at which we include sources to θ = 5′ (4′) one can compute the averagebackground by randomizing
would raise the noise in typical samples by 5% (15%). the positions of the sources and measuring the values ob-
tainedintheblank-fieldaperturesgenerated(e.g.,Lehmer
etal.2005). Hereweusebothprocedures: Weuseannular
measurements as our primary background determination,
andthenweuserandomizedpositionmeasurementstotest
that the procedure is not introducing offsets.
Before we continue, we note that the background we
are measuring is composed of several elements: an ap-
proximatelyuniforminstrumentalbackground,atrulydif-
fuse component containing contributions from hot inter-
stellar or intergalactic gas, and contributions from indi-
vidual sources below the direct detection threshold of the
deep CDF images. While a local estimate of the back-
ground contributions from the instrument and the diffuse
background should provide a good average measure, such
estimates could be more problematic for the unresolved
sources, which may be clustered. Clustering could, in
principle, result in an underestimate in determining the
background subtraction, since the annulus in which the
background is measured lies further from the source than
Fig. 3.— Relative S/N in the 2−8 keV band vs. aperture ra- the aperture in which the signalis measured. However,in
dius shown for five values of θ: 0′ or on-axis (black solid curve), practice, the surface density of X-ray sources at a given
1.5′ (red),3′ (blue),5′ (green),and7′ (blackdashed). Thevalueis
redshift is small, and the average contribution of these
normalizedtothepeakon-axisvalue.
sources to the background is also small. (Contributions
With the aperture specified, we can now compute the from sources at other redshifts may be viewed as random
X-ray counts s−1 as C = (S −B)/(f(r,θ)×t), where S with respect to the sources whose signal is being mea-
is the number of counts in the aperture, B(=πr2b) is the sured.)
number of background counts expected in the same aper- We may use the results of Section 5.2 to estimate that
ture,andtisthe effectiveexposuretime atthepositionof thetotalcontributionofallthesourcesinourphotometric
this aperture. C maybe negativeorpositive. Wetakethe redshiftsampleisapproximately2%oftheobservedback-
erroronthisquantitytobeE =B0.5/(f(r,θ)×t),since,in ground in the CDF-S. In smaller redshift intervals, these
6
contributions are correspondingly less and drop rapidly counts,while the lesssevereclipping (blue) does not. The
withincreasingredshift(seeSection6). Thus,theredshift 4 counts clip used in the present paper is the most strin-
intervalfromz =1−1.1producesabout0.001oftheback- gent clip possible that does not produce a significant off-
ground, and that at z =3−3.1 produces less than 0.0003 set. However,we note that the results are not sensitive to
of the background. These contributions are too small for choosing higher values for the clipping.
clustering in the galaxy population to perturb the back- Wecanseethisoffsetevenmoreclearlywhenweplotthe
ground in any significant way. two distributions of weighted mean 2−8 keV counts s−1,
In determining b, we use an annulus of radius 8′′ to L. (Red solid for the T11 procedure; blue solid for the
22′′. This choice of inner boundary avoids any contribu- present procedure.) The offset of the red solid histogram
tion from the target, and this choice of outer boundary (8.1×10−7±2.2×10−7 counts s−1) is almostidenticalto
providesalargeenoughnumberofpixels. Inordertoelimi- the weightedmeansignalfoundby T11forthe Bo06sam-
nateanycontributiontobfrombrightneighboringsources, ple (downward pointing arrow). In contrast, the offset of
we exclude 6′′ regions around known sources (13′′ regions thebluesolidhistogram(5×10−8±2.2×10−7countss−1)
around very bright sources), and we clip pixels with high is consistent with the zero weighted mean signal expected
counts. Considerable caution must be taken in perform- for random realizations if the background subtraction is
ingtheclip. Becausetheaveragenumberofcountsineach correct.
pixel is small, the counts distribution is Poissonian. Too The error in the simulations measured from the disper-
severe of a clip can introduce a downward bias in the es- sionintherealizationsisabout30%higherthantheformal
timation of the averagebackgroundin the annulus, which statistical error of 1.6×10−7 counts s−1, suggesting that
would result in a spurious signalwhen that backgroundis systematic effects may be present. Thus, we allow for this
subtracted from the counts in the aperture. This appears in assessing the significance of the detections.
to be the cause of the z ∼ 6 weighted mean signal found
by T11.
5. RESULTS
5.1. Secure Spectroscopic Redshift Sample
In Figure 5 we show the weighted mean counts s−1 in
both the 0.5−2 keV (red squares) and 2−8 keV (blue
diamonds)bandsversusredshiftforthe coresampleswith
secure spectroscopic redshifts. In (a) and (b) we show
the results, respectively, for the GOODS-S and GOODS-
N fields, and in (c) we show the results for the two fields
combined. The individual fields show a broadly similar
pattern. Ashasbeenfoundinpreviouswork(e.g.,Lehmer
Fig. 4.—Twodistributionsof2−8keVcountss−1,C,from100 et al. 2005), there is a strongly detected signal in the
realizations of randomly located apertures in the GOODS-S core 0.5−2 keV band out to z = 4 (see also Bomans, Zinn
regionforasamplewithasizeequal tothatoftheBo06sampleof
z ∼ 6 galaxies. The red dashed curve shows the results when the and Blex 2011). Beyond this redshift, even in the com-
background pixels are clipped above 2 counts (this corresponds to bined fields, the signal falls below the 3σ threshold, even
the T11 procedure), and the blue dashed curve shows the results when only the formal statistical error is used.
whenthebackgroundpixelsareinsteadonlyclippedabove4counts The weighted mean 0.5−2 keV counts s−1 in the com-
(present procedure). The solid line histograms show the distribu-
tions of the weighted mean 2−8 keV counts s−1, L. The more binedfieldsare5.2±1.0×10−7 countss−1 fortheredshift
severe clipping procedure of T11 (red) introduces an offset in the interval z = 3 − 4 and 7.2 ± 3.0× 10−7 counts s−1 for
distribution that is almost identical to the value measured in the z =4−5. The weightedmean2−8keVcountss−1 inthe
actual Bo06samplebyT11(downwardpointingarrow).
combinedfieldsareweakerandonlydetectedouttoz =3,
To test both the present procedure and the T11 proce- reflecting Chandra’s poorer sensitivity at these energies.
dure, we ran 100 realizations of randomly located aper- Converting the 0.5−2 keV (2−8 keV) counts s−1 to
turesintheGOODS-Scoreregionforasamplewithasize fluxwithanaveragemultiplicationof6.8×10−12ergcm−2
equal to that of the Bo06 sample of z ∼ 6 galaxies. In (23.9×10−12 erg cm−2), where the conversionfactors are
Figure 4 we show the two distributions of the 2−8 keV takenfromT11,wefindthefluxratiof(0.5−2keV)/f(2−
counts s−1, C, that we measured. In one case we clipped 8 keV)=0.91±0.15 at z =0−1, 0.95±0.23 at z =1−2,
the background pixels above 2 counts (red dashed curve; and 0.65±0.32 at z = 2−3. If the source spectra can
this correspondsto theT11procedure),whileinthe other be represented by power laws, then these flux ratios cor-
caseweonlyclippedthebackgroundpixelsabove4counts respond to photon indices of 1.93±0.13, 1.96±0.19 and
(blue dashed curve; present procedure). The more severe 1.69±0.28,respectively,showingthatthesourcesarequite
clipping(red)producesasystematicoffsetinthemeasured soft on average.
Cowie, Barger,& Hasinger 7
comparewith the GOODS-S secure spectroscopicredshift
sample in the same redshift intervals. In Columns (1)
and (2), we give, respectively, the minimum and maxi-
mum of the redshift interval. In Column (3), we give the
number of sources in the spectroscopic redshift sample.
In Columns (4) and (5), we give, respectively, the mean
0.5−2 keV and 2−8 keV counts with 1σ errors for the
spectroscopic redshift sample in units of 10−7 counts s−1.
In Column (6), we give the number of sources in the pho-
tometricredshiftsample. Finally,inColumns (7)and(8),
we give, respectively, the mean 0.5−2 keV and 2−8 keV
counts with 1σ errors for the photometric redshift sample
in units of 10−7 counts s−1.
Figure6issimilartoFigure5inthatweseeastrongsig-
nalouttoz =4 inthe 0.5−2keVbandbutnodetections
at higher redshifts. For example, for the redshift interval
z = 4−5, the weighted mean 0.5−2 keV counts s−1 is
1.38±0.62×10−7countss−1 orf(0.5−2keV)=9.4±4.2×
10−19 erg cm−2 s−1. We also again see a weak 2−8 keV
signal with respect to the 0.5−2 keV signal; it is only
detected in the redshift interval z = 1−3, where we find
a flux ratio f(0.5 − 2 keV)/f(2 − 8 keV)= 0.67 ± 0.15
corresponding to a photon index of Γ=1.7.
Fig. 6.— Weighted mean X-ray counts s−1, L, vs. redshift for
the sources with photometric redshifts in the GOODS-S core re-
gion. The red squares denote the 0.5−2 keV band, and the blue
diamonds denote the 2−8 keV band. Error bars are ±1σ. Also
shownaretheweightedmean0.5−2keVcountss−1 oftheBeck06
b, v, and i dropout samples (red open squares; these samples are
from the GOODS-S and HUDF) and the Bo06 i dropout sample
(red open triangle; this sample is from the GOODS-N, GOODS-S,
andHUDF).SourcesdirectlydetectedintheX11ortheA03X-ray
catalogsareexcluded. Noneofthez>4sampleshasanysignificant
signal.
Fig. 5.—(a)WeightedmeanX-raycountss−1,L,vs. redshiftfor
While the overallpattern with redshift is similar in the
all sources with secure spectroscopic redshifts in (a) the GOOD-S
coresample,(b)theGOODS-Ncoresample,and(c)thecombined spectroscopic redshift and photometric redshift samples,
core samples. The red squares denote the 0.5−2 keV band, and the weighted mean X-ray counts s−1 are more than a fac-
thebluediamondsdenotethe2−8keVband. Errorbarsare±1σ. tor of 2 lower in the photometric redshift sample than in
Sources directlydetected intheX11ortheA03X-raycatalogs are
the spectroscopic redshift sample. As we shall show in
excluded.
the discussion section (Section 6), this is a simple con-
sequence of the fact that the photometric redshift sam-
5.2. Photometric Redshift Sample
ple contains sources down to fainter optical magnitudes
In Figure 6 we show the weighted mean counts s−1 in than the spectroscopic sample. The photometric redshift
both the 0.5−2 keV (red squares) and 2−8 keV (blue sample, while containing the spectroscopically identified
diamonds) bands versus redshift for the sources in the sources as a subsample, probes to fainter optical magni-
GOODS-S core region with photometric redshifts. We tudes, and these optically fainter sources are intrinsically
give the results in tabular form in Table 1, where we fainter in the X-rays, reducing the weighted mean X-ray
8
Table 1
Mean X-ray Counts Per Second Versus Redshift: GOODS-S
Spectroscopic Sample Photometric Sample
z z N 0.5−2 keV 2−8 keV N 0.5−2 keV 2−8 keV
min max spec photz
(1) (2) (3) (4) (5) (6) (7) (8)
0.0 0.50 127 7.64±0.83 2.59±1.37 1170 1.59±0.28 1.41±0.46
0.50 1.0 350 9.81±0.50 2.55±0.81 2459 2.29±0.19 0.09±0.32
1.0 1.5 190 9.39±0.68 3.95±1.11 1500 3.35±0.25 1.50±0.41
1.5 2.0 25 12.2±1.81 0.09±2.95 817 3.76±0.34 1.76±0.55
2.0 2.5 38 9.66±1.68 4.67±2.78 835 3.00±0.33 1.52±0.54
2.5 3.0 32 8.00±1.82 4.04±3.04 697 2.10±0.36 0.15±0.58
3.0 3.5 24 7.82±2.09 1.19±3.48 430 2.46±0.46 0.21±0.76
3.5 4.0 14 9.00±2.43 -5.86±4.02 253 1.90±0.61 -1.03±0.99
4.0 4.5 6 -1.64±4.57 -8.19±7.65 145 1.00±0.81 0.07±1.33
4.5 5.0 0 ··· ··· 89 1.98±0.986 0.79±1.62
5.0 5.5 0 ··· ··· 46 0.50±1.33 .015±2.19
5.5 6.0 5 1.19±4.07 11.6±6.79 31 2.02±1.70 0.46±2.81
6.0 6.5 0 ··· ··· 6 3.64±3.59 -3.94±5.83
fluxes. However,because the photometric redshift sample find that the weighted mean 0.5 − 2 keV counts s−1 is
contains a larger number of sources, it identifies more of −11.4±5.1×10−8 counts s−1, while the weighted mean
theX-raybackgroundlight,asmeasuredbytheproductof 2−8 keV counts s−1 is −6.9±9.7×10−8 counts s−1. We
the number of sources per unit area and the mean counts conclude that high-redshift sources are generally too faint
per source, than the secure spectroscopic redshift sample. to be detected in X-rays, even in these extremely deep
At redshifts between z =0 and 1, the contribution to the stacks. The typical 2σ upper limits on the weightedmean
X-ray background light by the photometric redshift sam- fluxes are approximately 7×10−19 erg cm−2 s−1.
pleisabouttwiceasmuchasthecontributiontotheX-ray
backgroundlightbythesecurespectroscopicsample,while
between z =2 and 3, it is about six times as much.
The mean counts per source in the photometric red-
shift samples do not change rapidly as a function of red-
shift. Thus, the results are not very sensitive to catas-
trophic photometric redshift errors. If 4% of the sources 6. DISCUSSION
that the photometric redshift sample placed at z = 0−1 The X-ray fluxes probed by the optimized averaging
were really at z = 2 − 3, then the mean counts at analysis are, by construction, bounded above by the flux
z =2−3 would only change from 2.59×10−7 counts s−1 detection limits in the direct X-ray catalogs. As we illus-
to 2.55×10−7 countss−1. At z =3−4,the changein the trateinFigure7,evenathighredshifts,this placesanup-
mean counts would be even smaller. per bound onthe observed-frame0.5−2 keVluminosities
of ∼ 1042 erg s−1. We may therefore expect the sources
5.3. Dropout Samples
inthe averaginganalysisto be dominatedby star-forming
None of the dropout samples are detected in either the galaxieswithsomecontributionfromLLAGNs(e.g.,Bauer
0.5−2keVorthe 2−8keVbandsatanysignificantlevel. et al. 2004). The power law photon indices based on the
For the Beck06 b, v, and i dropout samples, we find that broadband X-ray colors (Γ = 1.7−2 for z = 1−3; see
the weighted mean 0.5−2 keV counts s−1 are 4.7±3.4× Section 5.1) are broadly consistent with this interpreta-
10−8 counts s−1 for z =3.74, 4.2±7.0×10−8 counts s−1 tion. Swartz et al. (2004) give an average Γ = 1.7 for the
forz =4.78,and2.5±12.3×10−8countss−1 forz =5.84. ultraluminous X-ray sources (ULXs) that dominate the
We show these with red open squares on Figure 6. X-ray contributions in strong star-forming galaxies. How-
For the Bo06 i dropout sample, we find that the ever, the photon indices of ULXs are poorly determined
weightedmean0.5−2keVcountss−1 is−10.7±5.3×10−8 above 10 keV, which adds some uncertainty to the com-
counts s−1 (red open triangle in Figure 6), while the parisonat the highest redshifts (z ∼3) for which we were
weighted mean 2 − 8 keV counts s−1 is −13.1 ± 9.7 × able to measure the weighted mean observed-frame flux
10−8 counts s−1. In contrast, T11 obtained a 2−8 keV ratios, f(0.5− 2 keV)/f(2− 8 keV). The dominance of
signalof88±13×10−8countss−1,whichishighlyinconsis- star-forming galaxies at the low X-ray fluxes is also sup-
tent withthe presentlimits. As we discussedinSection4, portedby fluctuation analyses,which show that the unre-
the T11 detection appearsto be the consequence ofincor- solvedfluxdistributionisconsistentwithanextrapolation
rect backgroundsubtraction. of the star-forming galaxy log N/log S (Hickox & Marke-
At higher redshifts (z ∼ 7 − 8; Bo11 sample), we vitch 2007; Soltan 2011).
Cowie, Barger,& Hasinger 9
Fig. 7.— Comparison of the weighted mean 0.5−2 keV lumi-
nosities (units of 1040 erg s−1) of the sources in the spectroscopic
(redsolidsquares)andphotometric(redopensquares)redshiftsam-
ples with the individually detected sources in the CDF-S (blue di-
amonds) and CDF-N (green triangles). Also shown are the on-
axisdetectionlimitsfortheCDF-S(bluecurve)andCDF-N(green
curve).
Fig. 8.— (a) The 0.5−2 keV contributions to the X-ray back-
grounddeterminedfromtheresultsofthepresentphotometricred-
shiftaveraginganalysisintheGOODS-Scoreregion(opensquares).
Dijkstra et al. (2011) predicted the X-ray sky surface
These contributions combined with the contributions from the di-
brightness (i.e., the X-ray background light) from star- rectly detected low X-ray luminosity sources in the X11 catalog
forming galaxies using the star formation history of Hop- give the total contributions to the 0.5−2 keV surface brightness
from sources withX-ray luminosities less than 1042 erg s−1 inthe
kins & Beacom (2006) and the star formation rate (SFR)
0.5−2keVband(solidcircles). (b)Sameforthe2−8keVcontribu-
to X-rayconversionof Mineo et al. (2011). This allows us
tions. Inbothcases,thesolidcurveshowstheDijkstraetal.(2011)
to make a very simple comparison of the light measured calculationinthe2−8keVbandofthecontributionofstar-forming
from the low-luminosity X-ray sources in the averaging galaxies to the X-ray background (for the assumption of a photon
indexofΓ=2,thisshouldequalthecontributioninthe0.5−2keV
analysis with the X-ray prediction made from star forma-
band), and the dashed curve shows the contribution of LLAGNs
tion histories measured at other wavelengths. In Figure 8 with X-rayluminosities less than 1042 erg s−1, as computed using
wecomparetheDijkstraetal.calculationinthe2−8keV themodelofGillietal.(2007).
band (black solid curve; we assume a photon index of
Γ =2) with the X-ray contributions determined from the The agreement between the averaging analysis results
results ofthe presentphotometric redshiftaveraginganal- (open squares) and the Dijkstra et al. (2011) prediction
ysis in the GOODS-S core region. In Figure 8(a) we use are extremely good. As expected from the discussion of
opensquarestoshowforthe0.5−2keVbandthequantity the photon indices, the 0.5−2 keV and 2−8 keV sur-
N × S/(A×(z −z )), where N is the number ofsources face brightnesses are almost identical and match to the
1 2
usedintheaveraginganalysis,Sistheweightedmeanflux, prediction for most of the z = 0 − 3 range over which
A is the observed area in square degrees, and (z −z ) is thepredictionwasmade,thoughthenoiselevelsaremuch
1 2
theredshiftinterval. Wecancombinethiswiththecontri- higher in the 2 − 8 keV sample. The only exception is
butions from the directly detected low-luminosity sources at low redshifts (z < 0.5), where the upper bound on the
in the X11 catalog to determine the value for all sources fluxexcludesmanyofthestar-forminggalaxies. Whenthe
with 0.5−2 keV luminosities less than 1042 erg s−1 (solid results from the directly detected low-luminosity sources
circles). Figure8(b)showsthesameplotforthe2−8keV in the X11 catalog are combined with the averaginganal-
band. ysis results (solid circles), the data also then agree with
10
the prediction at these low redshifts. Integrating through
the combined results, we find that a very large percent-
age of the contribution to the X-ray background from
L < 1042 erg s−1 star-forming galaxies comes from low-
X
redshiftobjects: 79%at0.5−2keVand83%at2−8keV
arise from z ∼< 2. We also show the contributions from
LLAGNs with L < 1042 erg s−1 to the 0.5 − 2 keV
X
and 2 − 8 keV surface brightnesses, as computed using
the model of Gilli et al. (2007). These can be significant
at z <1 but drop rapidly at higher redshifts.
We mayinvertthis anduse the X-raydatato construct
the star formation history as a function of redshift from
X-ray samples (e.g., Norman et al. 2004; Lehmer et al.
2008). We converted the total X-ray surface brightness
in the 0.5−2 keV band of all sources with luminosities
less than 1042 erg s−1 in each redshift interval to the
corresponding comoving X-ray luminosity density in the
0.5−8 keV band, assuming a photon index of Γ=2. We
then computed the SFR per unit comoving volume using
Fig. 9.—TheSFRperunitcomovingvolumecalculatedfromthe
the relation in Mineo et al. (2011). For the present data, 0.5−2keV sources withX-rayluminosities lessthan 1042 ergs−1
we cannot separate the various contributions to the X- (redsquareswith1σ errorbars)vs. redshift. Theblacksolidcurve
ray light, so rather than adopting the Mineo et al. (2011) shows the Hopkins & Beacom (2006) parametric fit to their star
formation history renormalized to a Salpeter IMF stretching from
best-fitting linearrelationobtainedfromonlythe resolved
0.1to100M⊙.
sample (their Equation 22), we used their linear relation
obtained from only the unresolvedgalaxies(given in their
Section 8.1):
With these data we can also address the evolution of
the relation between the X-ray luminosity and the SFR
as a function of redshift. This relation, L = c × SFR,
X X
depends on the initial mass function (IMF), the proper-
ties of binary stars, and the galaxy metallicities, among
other things. One might expect that the normalization,
c ,wouldbehigherinlow-metallicitygalaxies(e.g.,Book-
X
SFR(M⊙ yr−1)=2.7×10−40L0.5−8 keV(erg s−1). (1) binder et al. 1980; Dray 2006; Linden et al. 2010). There
is some weak evidence for this (Kaaret et al. 2011). In
turn, this might suggest that c could be higher at high
X
redshifts. Mirabel et al. (2010) invoke this evolution as a
possible reionization mechanism.
Dijkstraetal.(2011)triedtoconstrainsuchanevolution
using the contributions to the X-ray backgrounds. Their
results could only weakly constrain any evolution in c ,
X
Here the SFR is for a Salpeter (1955) initial mass func- but this might be due to the fact that the contributions
tion stretching from 0.1 to 100 M⊙. The normalization to the backgrounds from the higher redshifts are small.
is a factor of 1.4 higher than if we had instead used their We can more directly constrain any evolution in c as a
X
result for only the hard X-ray binaries. We note that this function of redshift by comparing how the X-ray flux de-
calibrationdoesdependonthestarformationhistory. We pends on the UV flux as a function of redshift. Since the
alsonotethattherehavebeennumerouscalibrationsofthe star formation histories, particularly at the highest red-
SFR with X-ray luminosity, and these vary by up to 40% shifts, are generally computed from extinction corrected
(Grimm etal.2003;Ranallietal.2003;Persic&Rephaeli UV luminosity densities, this is the most direct test we
2007; Lehmer et al. 2010; Mineo et al. 2011). Thus, the can make.
estimated SFR will be uncertain at least at this level. ForeachgalaxyintheGOODS-Scoreregionwithapho-
Weshowthestarformationhistorydeterminedfromthe tometric redshift, we computed the rest-frame UV magni-
X-raydatainFigure9,wherewecompareitwiththatde- tude at 2500 ˚A by interpolating between the four ACS
rivedbyHopkins&Beacom(2006)usingmultiwavelength bandsintheGOOD-Scatalogandthentranslatingthisto
data. The shape and normalization of the two curves are a bolometric flux, νf , evaluated at the redshifted wave-
ν
in very good agreement. The normalization agreement length. Therest-framebolometricluminosityat2500˚Ais
is probably overly good, since this could be changed by νL = 4πd2νf , where d is the luminosity distance. We
ν l ν l
any one of a number of factors, such as contamination restricted our analysis to z > 1 so that in our lower red-
by LLAGNs, cosmic variance, or the uncertainty in the shift intervals the above interpolation is valid. At z >2.6
X-ray to SFR conversion factor. As discussed above, the where the observed wavelength lies beyond the reddest
LLAGN contribution is probably most significant below band (F850LP) in the ACS data, we used the F850LP
z = 1, where it may result in the X-ray estimate of the magnitude alonetoestimate the rest-framebolometriclu-
SFR being high. minosity.