Table Of Content

Sudden collapse of a colloidal gel Paul Bartlett,1,∗ Lisa J. Teece,1 and Malcolm A. Faers2 1School of Chemistry, University of Bristol, Bristol BS8 1TS, UK. 2Bayer CropScience AG, 40789, Monheim am Rhein, Germany Metastable gels formed by weakly attractive colloidal particles display a distinctive two-stage time-dependent settling behavior under their own weight. Initially a space-spanning network is formed that for a characteristic time, which we define as the lag time τ , resists compaction. This d solid-like behavior persists only for a limited time. Gels whose age tw is greater than τd yield andsuddenlycollapse. Weuseacombinationofconfocalmicroscopy,rheologyandtime-lapsevideo imagingtoinvestigateboththeprocessofsuddencollapseanditsmicroscopicorigininanrefractive- indexmatchedemulsion-polymersystem. Weshowthattheheighthofthegelintheearlystagesof 2 collapseiswelldescribedbythesurprisinglysimpleexpression,h(τ)=h0−Aτ23,withh0 theinitial 1 heightandτ =tw−τd thetimecountedfromtheinstantwherethegelfirstyields. Weproposethat 0 this unexpected result arises because the colloidal network progressively builds up internal stress 2 as a consequence of localized rearrangement events which leads ultimately to collapse as thermal equilibrium is re-established. n a PACSnumbers: 82.70.Dd,83.80.Kn,64.75.Xc,83.50.-v J 4 2 I. INTRODUCTION has been attributed to channel formation within the gel [12, 13], the microscopic processes operating have never ] t Soft materials such as colloidal suspensions and emul- beenfullyestablished. Abettermicroscopicunderstand- f o sionsformaremarkablyrichvarietyofnon-ergodicstates ing of the origin of sudden gel collapse is important not s [1–3] – examples of which are familiar to us in our daily only because the distinctive settling behavior is intrigu- t. life in products as diverse as foodstuffs, surface coatings, ingfromascientificviewpointbutalsobecauseaquanti- a m fabric conditioners, and pesticides. Out-of-equilibrium tative prediction of gel stability is a critically important phases occur when suspensions are quenched deep into issue in the formulation and manufacture of many com- d- a region of thermodynamic phase separation. Unable mercial products. n to phase separate, amorphous solids form which are me- The aim of this paper is to report a detailed experi- o chanically rigid but without the long-range translational mental study of the stability of gels under gravitational c order characteristic of crystalline solids. Slow relaxation stress. We use a colloidal suspension of nearly monodis- [ dynamics prevents the system from reaching their un- perse emulsion drops of radius a suspended in an index- 2 derlyingglobalequilibriumconfigurationssotheseamor- matchedmixtureofsolvents,whichhasbeenwellcharac- v phoussolidsevolveslowlyinacomplexenergylandscape terized elsewhere [17]. Gelation is induced by long-range 3 with a high number of local minima and as a result dis- attractivedepletionforces. Usingtime-lapsevideoimag- 9 play glassy dynamics with a rich phenomenology of ef- ing we measure the dependence of the height h of a gel 8 fectssuchasaging,non-linearresponses,andspatialand upon its age t , counted from the moment when the gel 4 w . temporal dynamic heterogeneities. was formed. No macroscopic sedimentation is observed 9 One of the most dramatic macroscopic manifestations initially but after a period of latency the gel undergoes 0 ofagingisthephenomenonofsuddennetworkcollapsein a rapid collapse as the system separates into colloid-rich 1 gels. Gelsconsistofanetworkofparticleslinkedtogether and colloid-poor phases. We investigate the collapse dy- 1 : by long-lived attractive bonds. Sedimentation or cream- namics as a function of the strength −Uc/kBT of the at- v ing of the particles within a gel imposes a buoyant stress tractive interactions and the initial height h of the gel. i 0 X on the network which since gels are intrinsically rather Remarkablywefindthatwhencollapsestartsthechange r delicatehasdramaticconsequencesformicroscopicstruc- in the height of the gel ∆h = h0 −h follows a simple a ture and dynamics [4–6]. Weak gels, where the strength universal dependence on t which is independent of the w of the attractive potential at contact U is only a few initial height h of the gel. The observation of height- c 0 k T, show, for instance, a very unusual mechanical re- independentcollapseissurprisingandcontrastswiththe B sponse. Initially, the gel behaves as a solid but after a marked height dependence seen in short-range gels stud- finite lag time τ , the gel yields and catastrophically col- ied to date [13, 18, 19]. Using a combination of rheol- d lapses. Sudden or ‘delayed’ network collapse is observed ogy, confocal microscopy and time-lapse video imaging inawidevarietyofmaterials[7–16]andseemstobeubiq- we speculate that the collapse of the gel network occurs uitous at small U /k T. However, while sudden collapse as a result of irreversible aging, via a spatially heteroge- c B neous process of localized ‘micro-collapses’, which leads to a build up of internal stress within the gel and its ultimate failure. ∗ Correspondingauthor:[email protected] The paper is organized as follows: Section II discusses 2 the preparation of the emulsion gels studied and the ex- the index-matched PDMS drops so that the colloid-rich perimental techniques used. Section III details experi- phase appears dark in transmitted light. The colloid- mental results from both macroscopic and microscopic polymer mixtures were thoroughly mixed at the start measurements on the settling behavior of suspensions of of the experiments before being loaded into cylindrical attractive particles. The interpretation of the results in glass vials with an internal diameter of d=17 mm. The termsofinternalstressrelaxationsisdiscussedinSec.IV cell diameter was varied between 15 – 23 mm and both before we summarize our main findings in Sec. V. cylindrical glass and poly(styrene) cells were used, with no significant change in collapse behavior. To eliminate air bubbles which lead to irreproducible settling dynamics we used a gentle slow tumbling of the sample vial to II. MATERIALS AND METHODS thoroughly mix the samples before observation. Repeat experiments showed that following this protocol the col- A long-range attractive interaction was induced be- lapse kinetics could be measured with a reproducibility tweenemulsioncolloidsbypolymerdepletion. Theemul- of about 10-15%. sionconsistedofpoly(dimethylsiloxane)dropsdispersed in a solvent mixture of 1,2-ethane diol (ED) and wa- Rheological measurements were performed at 23◦C ter (mass fraction of ED = 0.59). The solvent compo- with a Bohlin HR Nano rheometer (Malvern Instru- sition was adjusted to closely match the refractive in- ments). To study simultaneously the temporal evolution dex of the emulsion to minimize van der Waals attrac- of the elastic properties and the height of the gel a novel tionsbetweendropsandtoenableconfocalimagingtobe rheometricvaneexperimentwasdevelopedwhichallowed conducted deep within the sample. A particle radius of visualobservationofthegelasrheologicalmeasurements a=316 ± 11nmandasizepolydispersityof0.17±0.07 were performed. The vane was made from stainless steel was determined from dynamic light scattering measure- and consisted of four blades (diameter 22.7 mm, height ments. The thickness of the polymeric stabilizing layer 10mm). Thevanewascarefullyinsertedintoclearpoly- surrounding each emulsion drop was evaluated by cen- carbonatesamplevials(diameter25mm,height65mm), trifuging a suspension and equating the packing fraction 10 mm below the top surface of the gel and a thin layer of the sediment to the jamming density of a hard sphere of silicone oil added to minimize evaporation. The vane systemwiththesamepolydispersity[20]. Thisprocedure remainedinsidethedenseupperphaseforthedurationof gave a layer thickness of ≈ 7±1 nm. The density mis- therheologicalexperiments,allowingthecollapseprocess matchbetweenemulsiondropsandthecontinuousphase to be continuously monitored. Oscillation measurements is ∆ρ = −130±10 kg m−3. To induce a depletion in- were performed at 0.5 Hz at intervals of 200-250 s under teraction, we added the non-adsorbing anionic polymer controlled stress conditions, within the experimentally- xanthan(Kelco,M =4.66x106gmol−1). Thepolymer determined linear viscoelastic region, while the height of w radiusofgyrationwasdeterminedasr =194±10nmby thegelwasmonitoredsimultaneouslybytime-lapsevideo g light scattering and viscometry. The strength of the de- microscopy. The absence of wall slip was confirmed by pletion attraction generated is a function of the polymer watching the movement of small air bubbles deliberately concentration and its range is controlled by the relative introduced into samples. size r /a=0.62±0.04 of the polymer and particle. The To directly probe changes in the microscopic topology g polymer concentration is quoted here in terms of the di- of the gel during collapse we used fluorescent confocal mensionless ratio c /c∗, where c∗ =3M /4πr3N is the microscopy. The continuous phase of the gel was la- p p p w g A overlapconcentration(c∗ =0.25mg/ml)andN isAvo- beledwith0.02mg/mlofthefluorescentdyerhodamine- p A gadro’s constant. Full details of sample preparation are B which combined with the high transparency of the contained in Teece et al. [17]. emulsions provided by refractive-index matching allowed To monitor the collapse of the gels we used time-lapse high resolution optical visualization deep within the gel. videorecordingtorecordimagesoftheemulsionsasthey A light microscope (Zeiss, Axioskop S100) was mounted cream. Alowmagnificationimageofthesettlinggelwas horizontally on its side, at right angles to gravity, and projected onto a CCD camera (Allied Vision Technolo- two-dimensional fluorescent images of regions 146 × 146 giesF-080B).Aregularsequenceofimageswascaptured µm were acquired at 543 nm. The gel was contained in every 20 seconds. The image series was corrected for op- a square cross-section glass vial, with an internal dimen- tical distortion and non-uniformities in illumination be- sionof13mm,mountedonalowprofiletranslationstage forebeingcalibratedusinganaccurategridoflines. The so that the gel could be imaged at different vertical po- images near the center of the cells were analyzed and sitions, throughout the full 30 mm height of the sample the interface separating the upper (dark) phase from the [17]. Since the emulsion drop radius is below the optical lower (bright) phase was identified automatically using resolution limit of the confocal microscope we can not an image analysis routine. The height h of the interface identify individual drops. Instead, we concentrated on was extracted as a function of time with an accuracy of the larger scale structure of the gel. The bicontinuous about ±0.3 mm. To aid visualization a low concentra- network was identified by thresholding the confocal im- tion (≈ 0.001 mg/ml) of an adsorbing black dye, Sudan agestodeterminethelocationoftheinterfaceseparating black, was added. 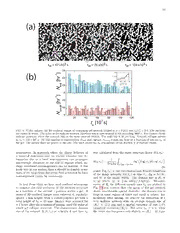The dye preferentially partitions into the (dark) emulsion phase from the (bright) continuous 3 (a) 25 50 100 150 200 250 300 350 400 (b) FIG. 1. (Color online). State diagram showing gels studied. The solid curve corresponds to the gas-liquid binodal calculated from the generalized free volume theory [22], for a polymer-colloid size ratio rg/a = 0.62. The open triangles identify the experimentally determined phase boundary. The theoretical prediction for the critical point is shown by the filled circle. The region below the coexistence line can be separated into two kinetic regimes: a region of complete FIG. 2. (Color online). Sudden collapse of a gel. (a) Time- demixing (I), and gelation (II). Quenched into region II, sus- lapse images of an emulsion-polymer mixture, with compo- pensions form a space-spanning network consisting of thick sition φ = 0.21 and c /c∗ = 3.6, as a function of the time p p strands of particles. The vertical line indicates the constant aftershaking. Eachimageislabelledbythetimeelapsedtw, colloid volume fraction gels studied (φ=0.213). The colored in units of 103 s. The initial height h of the sample is 40 0 symbols represent estimates of φ for the strands of particles mm. The characteristic delay time τ after which the net- d (bluesquares)andthecoexistinggas(redsquares)afterphase workstartstocollapseisindicatedbythedashedarrow. The separation is complete locally. Error bars represent the age- solid line denotes the position of the interface between the dependent variation in φ from the same sample. upper colloid-rich and lower polymer-rich phases. (b) The normalizedheighth/h ofthegelshowninpart(a)asafunc- 0 tion of the elapsed time showing the three stages of settling phase. To correct for in-plane variation in the fluores- characteristic of sudden collapse. cence yield, each image was divided into 16 sub-images andalocalthresholdforeachsub-imagewasdetermined using a cluster-based algorithm [21]. A careful analy- tween the calculated gas-liquid binodal and experiments sis of the resulting binary images, backed up by direct isgoodconfirmingthattheexperimentalsystemisaccu- observation, showed that this approach reliably located rately represented by a simple mixture of hard spheres the shape and positions of the emulsion and aqueous do- and non-adsorbing polymer chains. mains. Thesuddencollapseofgelswasinvestigatedasafunc- tionofboththestrengthoftheattractions−U /k T and c B theinitialheighth ofthesample. Intheabsenceofpoly- 0 III. EXPERIMENTAL RESULTS mer,emulsionsremainedstableandshowednonoticeable separation so the mechanical instability seen is a conse- A. Collapse dynamics quenceofaggregateformation. Theprocessofcollapseis exemplifiedbythetime-lapseCCDimagesreproducedin To begin, the phase behavior of mixtures of emulsion Fig. 2(a). Qualitatively we identify three distinct stages, and polymer was investigated as a function of both the characterizedbytheinterfacevelocityν =dh/dt ,where w emulsion volume fraction φ and polymer concentration t is the age of the gel. During an initial lag period (I) w c /c∗. The state diagram plotted in Fig. 1 summarizes the network of attractive particles produces a mechani- p p the results and shows the locations of a stable liquid cally stable solid, which is capable of supporting its own phase, a narrow region of equilibrium gas-liquid demix- weight. This regime of solid-like stability persists how- ing(I)andabroadzoneofnon-equilibriumgelation(II). ever only for a limited duration. On times longer than The generalized free volume predictions (GFVT) [22] for τ , the lag time, the network yields and a clear interface d apolymer-colloidsizeratior /a=0.62inagoodsolvent appears (identified by the solid line in Fig. 2(a)). The g areshownbythesolidlinesinFig.1. Theagreementbe- interface velocity ν grows smoothly as the gel shrinks 4 (a) and the collapse becomes progressively more rapid. This period (II) of rapid collapse terminates when phase separation nears completion and the interface approaches the final equilibrium plateau. In the final consolidation stage (III), the settling velocity drops markedly as the collapsed gel continues to slowly compress like a solid under its own weight. The lag time τ is a strong function of the polymer d concentrationandhencethestrengthofdepletionattrac- tions. Fig 3(a) shows the time-dependent height h(t ) w of gels prepared with different polymer concentrations but for the fixed initial height h = 40 mm. Inspection 0 reveals two striking features. First, as reported in pre- (b) vious work [10, 11], τ grows strongly with increasing d polymer concentration. Indeed the concentration dependence of the lag time is well described by the exponential relationship, τ ∼exp(c /c∗), as shown in Fig. 3(c). d p p Δ Second, the sedimentation profiles are remarkably similar in shape when plotted in a linear-log representation. τ3/2 The height profile at a low polymer concentration may be simply mapped onto a high concentration sample by Δ shifting the collapse profile to the right along the loga- rithmictime-axis. Toexplorethisscalingbehaviorquan- titatively, we focus purely on the collapse regime and replot the change ∆h = h −h in the height of the gel τ3/2 0 as a function of the shifted time variable τ = t −τ , w d thetimecountedfromtheinstantwhenthenetworkfirst (c) yields. Fig.3(b)demonstrates,ratherunexpectedly,that theinitialchangeintheheightofthegeldependslinearly upon τ3/2, over a wide range of polymer concentrations. In the early stages of gel collapse, where ∆h (cid:46) 0.5h , 0 the height of the gel follows approximately the algebraic expression h(τ)=h0−Aτ32 (1) where A is a polymer-dependent prefactor. The exis- tence of this simple relationship suggests a single com- mon mechanism is controlling the collapse of the gel at different polymer concentrations. We return to a more detailed discussion of this point in Sec. IV to speculate onapossibleoriginoftheτ32 scalingfoundhere. Finally, FIG.3. (Coloronline). Gelcollapseatfixedheight. (a)Time we note that an alternative scaling has been suggested evolution of gel height for different polymer concentrations. by Kilfoil et al. [23]. We found however that their ap- Only data in the lag and collapse regimes is shown for clar- proach failed when applied to the wide range of polymer ity. (b)Thechange∆hinheightasafunctionofτ3/2,where concentrations and heights studied here. τ = tw −τd is the time elapsed from the start of collapse. Previousstudies [13,24]of gelcollapse havesuggested Symbols and data are the same as in (a). The solid lines are thatthemechanismofcollapsedependssensitivelyonthe straight line fits. The inset shows an expanded view of the short-timedata. (c)Comparisonbetweentheexperimentally- initial height h of the gel. Gels formed in short sample 0 measuredlagtimesτ (filledpoints)andtheaveragelifetime cellsdisplaysteadyor‘creeping’sedimentationwherethe d height falls continuously with age at a rate which decays τesc of an individual particle bond (solid line). Lag times were measured in both glass (triangles) and poly(styrene) exponentially with time while taller samples show sud- vials (squares). The dashed line, which reproduces the ex- den collapse. To test whether this behavior is intrinsic perimental data reasonably well, equates to a fixed number to the long-range systems studied here we have varied of bond lifetimes (τd ≈240τesc). the initial height h and monitored the evolution of the 0 height of the gel with time. In all the samples reported here, polymer concentration from c /c∗ = 2.4−4.0 and p p heightsh =22−63mm,suddengelcollapsewasalways 0 observed and we saw no transition to creeping sedimen- 5 pension below, so σ = ∆ρgφh . Taking φ = 0.21 and g 0 ∆ρ=−130 kg m−3 we estimate that σ varies from be- τ g tweenapproximately5to15Pafortheheightsusedhere. (a) The values for the buoyant stress considerably exceeds the yield stress of the gel network, which we estimate from rheological measurements as σ ∼ 0.1 Pa, so even y while σ is an order of magnitude larger than the stress g required to break the gel’s load-bearing structure the gel does not collapse macroscopically. The insensitivity of τ to h means we can rule out the possibility that the d 0 initial period of latency of the gel is determined purely by the breaking of single uncorrelated bonds. Collapse clearly requires a substantially larger degree of restruc- turing of the network than is necessary simply for mechanical yielding. To explore the effect of height on the kinetics of col- (b) c / c* 106 2P.4p lapse we focus on the initial rate of collapse of the gel 3.2 with different h . Figure 5 shows that the power-law ex- 3.6 0 4.0 pression (Eq. 1) which captures well the height variation ] in gels with a fixed h also holds for gels with a wide s 0 [ 105 variety of different starting heights. The gel does not τd collapse with a fixed time-invariant velocity but rather the interface velocity ν = dh/dτ behaves at short times 104 like τ1/2, a behavior which hints at a surprisingly novel mechanism of collapse. To further investigate this mechanism we have studied the dependence of the prefactor 20 30 40 50 60 70 A=d∆h/dτ3/2ontheheightandpolymercontentofthe h [mm] gel. Fig. 5(c) shows that rather remarkably, for all the 0 gelsstudied,theprefactorAdoesnotchangewiththeini- FIG. 4. (Color online). Height-independent lag times. (a) tialheightofthegel. Sincethegravitationalstressσ on g Temporal evolution of a gel with different initial heights but the gel increases linearly with its height, this result sug- a fixed composition, φ=0.213, and cp/c∗p =3.6. The arrows geststhatσgisrelativelyunimportantindeterminingthe indicate the lag time τd. (b) The lag time τd as a function process of collapse, at least under the conditions of our of the initial height h of the gel, for a number of different 0 experiments. Thecentralroleofthermally-inducedbond polymer concentrations. The open symbols denote data ob- dissociation is seen in Fig. 5(d) where it is revealed that tained in glass-walled cells while the filled symbols indicate the prefactor A scales exponentially with c , equivalent measurements in poly(styrene) cells. The nature of the cell p to an exponential dependence on the depth of the inter- wall has no noticeable effect on the delay time measured. action potential. In conclusion, the process of collapse appears to be thermally rather than stress-activated. tation. Fig.4(a)showsarepresentativesetofdatawhere To interpret these striking observations we model the thetimeevolutionoftheinterfaceheighth(t )isplotted initial deformation of a gel using the poroelastic formal- w for a range of initial heights and a single polymer con- ism first introduced by Buscall and White [25]. In this centration (c /c∗ = 3.6). Inspection of the data reveals approach the gel is treated as a biphasic fluid-saturated p p that rather surprisingly the time τ during which the gel porous continuum with the pore pressure P as a state d is solid-like is largely independent of the initial height variable. A gel consists of two distinct phases: a solid h of the sample. Measurement of the variation of τ phase of connected strands of emulsion particles, and a 0 d with height for a wide range of polymer concentrations, secondliquidphaseconsistingofafluidsolutionofanon- presented in Fig. 4(b), confirms this observation. We adsorbingpolymer. Intheearlystagesofcollapsethegel havecheckedthatthisisnotduetosolidfrictionbetween is essentially uncompressed so there is no elastic stress the gel and cell wall [19] by repeating measurements at due to deformation and the rate of collapse is limited es- c /c∗ = 2.4 using cylindrical poly(styrene) cells to alter sentially by the rate at which fluid is forced out of the p p the degree of wall adhesion. The results, shown as the gel [18]. Defining v as the macroscopic velocity of the filled data points in Fig. 4(b), are in excellent agreement fluid flow through the gel and w as the local displace- with the data obtained in the glass vials (open points), ment of the solid network along the gravitational z-axis demonstrating that wall friction is unimportant. then using Darcy’s law, Since the gel is initially a solid, the top of the sample vial is subject to a gravitational stress σg, which is η(1−φ) generated by the full buoyant stress of all of the sus- −∂zP = k (v−∂tw), (2) 6 where k is the permeability of the network, which since an average over regions where the gel has broken apart, we are considering only the early stage of collapse we and is a fluid, with other portions of the network which assume to be height independent, and η is the viscosity remain elastic. The recorded response will then depend of the continuous phase. Continuity demands on the relative sizes of the mechanical vane and the in- homogeneousregionswithinthegel. Toconfirmthatthe (1−φ)v =−φ∂ w (3) t sample becomes a fluid when the gel begins to collapse we have placed a small glass block about half the width which, since φ<1−φ, implies that the fluid velocity |v| of the cell in the base of the cell. When the gel begins mustbesmall[18]incomparisonto|∂ w|. Consequently, t to collapse the interface between the gel and the bottom if the displacement of the gel varies as τ3/2 then, from ofthecellrapidlyflattensindicatingthatthebaseofthe Eq. 2, the pressure gradient at the top of the gel, adja- gel becomes a fluid of aggregates as the gel collapses. cent to the interface, must be increasing as τ1/2. This time dependence rules out a simple compression of the Whiletherheologicalmeasurementsprovideamechan- gel as a consequence of gravity because the pressure gra- ical insight into gel settling, they do not clarify the link dient would then be a constant, ∂ P =−∆ρgφ, and the between the macroscopic processes of collapse and the z gelwouldaccordinglyshrinklinearlywithtime[18]. The microscopic structural reorganization occurring during τ1/2 dependenceofP suggestsinsteadadiffusiveprocess aging and sedimentation. Indeed, at first sight, it seems may be responsible for the unusual collapse dynamics counter-intuitive that a gel which is becoming gradually seen. Wecanhoweverruleoutabulkdiffusiveprocessof stiffer with time should ever collapse at all. To probe conventional syneresis, akin to the shrinkage of a poly- thelinkbetweenthemicroscopicandmacroscopiclength mer gel undergoing a phase transition [26]. In this case, scales, we have examined the temporal evolution of the the contraction of the matrix as the phase separation gelmicrostructureusingconfocalmicroscopy. Thecoars- ensues would generate an increase in P which leads to ening is illustrated by the binary two-dimensional im- the expulsion of fluid and a shrinkage of the gel as t1/2 ages reproduced in Fig. 7. In the rectangular cell used [27] rather than the t3/2 dependence seen here. Further- for imaging experiments, the delay time was measured more, this process would require fluid to be transported as τd ≈ 1.3×105 s so both images refer to the latency through the full length of the system so the rate of diffu- period before collapse starts. Clearly, although the gel sion would depend on the height of the gel, which is also remains mechanically stable during this period there is incompatible with our data. Clearly, a new mechanism a slow but continuous evolution in the microscopic na- is required to correctly explain the observed data. ture of the particle network and the system is not arrested. A closer look at the data in Fig 7 reveals that the interface between the continuous and particle phases B. Microstructure is quite rough, suggesting that surface tension is unimportant and the dense portion of the gel is not a fluid. Directobservationshowthatparticlediffusionisstrongly Sudden collapse reflects a dramatic loss of mechanical suppressed and particles move infrequently between the integrityasthegelages. Tounderstandthenatureofthis strands of the network, indicating that the interaction mechanical failure, we first examine the evolution of the networkisprobablyglassy. TheimagesinFig7illustrate elastic properties of the gel while simultaneously record- two further microstructural characteristics which will be ing the height of the gel. Figure 6 shows the rheology important to our later discussion on the mechanism of and interface height h(t ) during the settling of a repre- w network collapse. First, it is evident that the thickness sentative gel. At the earliest times recorded, the sample is solid-like with an elastic shear modulus G(cid:48) which is of the backbone of the gel grows slowly but continuously larger than the viscous modulus G(cid:48)(cid:48). The measurements with time, a fact which probably explains the increase of G(cid:48) with t seen in Fig. 6. Second, the thickness of however reveal that the elasticity of the gel far from re- w the network of particle strands is not uniform. The gel ducing with time, as one might naively expect, actually containsarelativelylargenumberofthinjunctionpoints increases continuously up to the point t =τ when the w d gelstartstocollapse. Immediatelycollapsestarts,G(cid:48)also where two or three arms (in 2D) are connected together. Simultaneousbreakageoftheparticlebondsattheserel- drops, but only by a relatively small amount (less than atively weak junction points would lead to a rapid break 10%),beforefinallygrowingsteadilyastheemulsionvol- up of the whole network. ume fraction in the upper phase increases with the onset of phase separation. We see no sign of large-scale hy- To quantify the change of the microstructure with drodynamic mixing, recirculation, and the development time, we use chord methods developed to analyze sta- of channels which have been seen in some other stud- tistically random heterogeneous materials [28]. We su- ies of gravitational collapse [8, 12, 13]. It is intriguing perimpose on the images of Fig 7 a uniform grid of hori- that even though G(cid:48) drops at the initiation of collapse zontalandverticallines. Thetwo-phaseinterfacesdivide the overall mechanical response remains predominantly eachgridlineintochordsthatareeitherinsidethedense elastic (G(cid:48) > G(cid:48)(cid:48)). We suspect that this reflects the in- part of the network or else lie within the solvent back- homogeneous nature of the network at collapse. If the ground. We define a chord as the line segment between sample is heterogeneous the response measured will be twoconsecutiveintersectionsoftherandomlinewiththe 7 60 (a) 63 mm 60 (b) 63 mm 55 mm 56 mm 47 mm 46 mm 50 38 mm 50 39 mm 31 mm ] 30 mm m] 40 22 mm m 40 22 mm m m [ [ 30 h 30 h 20 20 10 10 0 1 2 3 4 5 0.0 0.1 0.2 0.3 τ3/2 [ 108 s3/2] τ3/2 [10 8 s3/2] 102 10 c / c* p p (c) 4.0 (d) 3.6 ] 101 3.2 -3/2 s 22..84 -3/2s] 1 m 100 m n n [ A A [ 0.1 10-1 10-2 0.01 20 30 40 50 60 70 2.0 2.5 3.0 3.5 4.0 h [mm] c / c* 0 p p FIG. 5. (Color online). Initial τ3/2–collapse dynamics. (a) The height h of a gel plotted as a function of the 3/2–power of the time elapsed after the gel yields, for different initial heights h . Curves are labelled by the initial height. The samples 0 have fixed polymer concentration c /c∗ =3.6, and colloid content φ=0.213. (b) Similar time-dependent settling observed in p p gels with c /c∗ = 2.4. (c) Invariance of the prefactor A = −lim dh/dτ3/2 with the height of the gel. Curves are labelled p p τ→0 by c /c∗. (d) Exponential dependence of A on the polymer concentration, highlighting the activated nature of the collapse p p process. bounding two-phase interface. Focusing only on those whichweuseherebecauseitdisplaysasmallerstatistical chords that lie within the dense strands of the network, error. Finally, the chord functions also provide an effi- we count the number of chords N(l) with lengths in the cient means to estimate the volume fraction of the high range l and l+dl. If N is the total number of chords density colloidal regions in the gel. If we assume the gel then the degree of linear ‘connectedness’ of the gel may is isotropic and the two-dimensional images are chosen be characterized in terms of a probability density func- randomly then the fraction χ of the volume of the gel tion, p(l), where occupied by the dense regions is N(l) 1 (cid:88) p(l)dl= . (4) χ= N(l)l (6) N L l The quantity p(l)dl is the probability that a randomly- where L is the total length of the original lines. The chosen chord has a length between l and l+dl. We find volume fraction of colloids, φ , in the dense regions of that the chord length distribution p(l) displays a char- g the gel is given by the ratio φ/χ, where φ is the initial acteristic shape, with p(l) first increasing with growing l colloid volume fraction. before reaching a maximum at a finite l and finally de- Next we characterize the slow evolution of the gel caying exponentially for larger l. The diameter of the structure. Fig. 8 shows the age dependence of the mean strands of particles within the gel may be characterized chord length l and the volume fraction φ prior to col- either from the value at which p(l) takes a maximum g g lapse. Akeyobservationisthatduringthelatencyperiod value or from the mean chord length l g when the height of the gel is unchanged structural reor- (cid:90) ∞ ganization is never fully arrested but continues, albeit l = lp(l)dl, (5) g rather slowly. So, for instance, the growth of the mean 0 8 2 .5 5 0 ] h ( t ) a 2 .0 w 4 0 (a) P [ ) tw1 .5 G ’ ( t ) 3 0 ] ’’ ( w m , G 1 .0 G ’’ ( t ) 2 0 [m ) h w w (t 0 .5 1 0 ’ G 0 1 2 3 4 5 6 1 0 1 0 1 0 1 0 1 0 1 0 t [ s ] w FIG. 6. (Color online). Simultaneous measurements of linear viscoelasticity and height h of gel as a function of time 0 .6 elapsed since preparation tw. Gel had an initial composition (b) of c /c∗ = 3.6, φ = 0.213 and a measured delay time of p p τ = 1.2×105 s (indicated by dashed line). The elastic G(cid:48) d and loss G(cid:48)(cid:48) moduli were measured by applying a oscillatory f stress of magnitude 0.0025 Pa at a frequency of 0.5 Hz and 0 .5 measuring the strain response. The gel stiffens continuously g c / c* withageuntiltheelasticmodulusdropsattw =τd asthegel p 2 .2 p begins to collapse. 2 .4 2 .8 3 .2 0 .4 1 0 2 1 0 3 1 0 4 1 0 5 1 0 6 ((ΑΑ)) ((ΒΒ)) t [ s ] w FIG. 8. (Color online). Evolution of colloidal network with time. (a)Averagechordlengthlginthecolloidphase,inunits of the particle diameter. The rate of increase of lg is always slower than the diffusive growth, lg ∼t1w/3 (shown by dashed line) characteristic of classical spinodal decomposition [29], 2200 μm 2200 μm andslowsdownconsiderablywithincreasingpolymerconcen- tration cp/c∗p. (b) Average colloid volume fraction φg within FIG. 7. Continuous coarsening of gel with age. Two- dense regions of the gel, as a function of elapsed time. The dimensional binary representation of a gel with composition density of the particle strands within the network increases c /c∗ =2.4,φ=0.213after(a)3.6×103s,and(b)1.12×105s progressivelywithagebeforerisingrapidlyattheonsetofgel p p from preparation. Gravity points vertically downwards and collapse. the scale bar corresponds to 20 µm. C. Origin of lag time Having characterized the macroscopic process of col- chord length is well described by a power law, lg ∼ tαw, lapse,wenowdiscussthemechanismfortheinitialfailure with an exponent α. The growth law is always much oftheparticlenetwork. Agelisametastablephasewith slower than the t1/3 dependence expected for the diffu- a high free energy density whose consolidation is driven w sive regime of classical liquid-gas phase separation. The ultimatelybythethermodynamicdrivingforceforphase growth exponent α depend rather strongly on the poly- separation. Howeveronceastablepercolatingnetworkof mer concentration with α decreasing markedly as c /c∗ strands of particles is formed the dynamics of phase sep- p p isincreased. Similarslowgrowthhasbeenidentifiedpre- aration is slowed down considerably because, as evident viously in simulations of deep quenched Lennard-Jones from Fig. 7, the strands of the network are many parti- systems [29] and has been interpreted as indicating that cles wide so large scale rearrangements of the gel require the dense domains of the gel are actually glassy. the simultaneous dissociation of all of the particle bonds 9 within the cross-section of a strand, which will be very escape time. This strong correlation highlights the piv- rare. The network accordingly lowers its free energy via otalroleofspontaneousthermalfluctuationsindetermin- a series of small-scale structural reorganizations which ingthelatencyperiodofthegel. Thefactthatthedelay proceed through the rupture of essentially single parti- time is many times longer than the rupture of a single cle bonds. The breakup of an energetic bond between bond probably reflects the cooperative nature of gel fail- particles, diffusion to dense region of the network, and ure. Thestrandsofthenetworkareseveralparticleswide a reformation of the broken bond allows a net increase so failure requires the simultaneous dissociation of all of in the number of nearest neigbouring particles with a the bonds in the cross-section of a particle chain [31]. concomitant lowering of the free energy of the system. The alternative picture proposed by Buscall et al. [32], For the network to coarsen, the system must overcome that the ratio τ /τ is determined by the mean coordi- d esc theenergeticbarrierassociatedwithsinglebondrupture. nation number of particles within the gel, could only be This could be achieved, in principle, either thermally or consistent with our observations if the mean particle co- as a result of an applied stress. The observation that ordinationnumbervariedwiththedepthoftheattractive the delay time is unaffected by the initial height of the potential. To distinguish completely between these two gel strongly suggests that the delay time and hence the possibilities requires a more detailed microscopic model rupture of individual bonds is controlled primarily by of gel failure than is currently available. thermal fluctuations rather than being stress-driven. To explore the microscopic mechanism by which ther- To calculate the average lifetime τ of an individ- malfluctuationsleadtodelayedfailureweusedreal-space esc ualparticlebondduetothermalfluctuations,weassume confocal imaging to follow the time evolution of the gel. that a single bond ruptures on a scale comparable to Since the load-bearing nature of the network is clearly the time it takes a Brownian particle to escape from an important we concentrate on changes in the connectiv- attractive ramp potential with the same range δ/a and ity of the strands of particles which constitute the gel. depth −U /k T as the interparticle depletion potential. Figure 9(a) shows two-dimensional confocal slices taken c B The mean escape time in the overdamped limit is given from the same physical region within an aging gel be- by the Kramers expression [30] fore collapse occurs. Because of the finite bond energy, the network structure slowly but continuously evolves, δ2 exp(−U /k T)−(1−U /k T) with fluctuations in both the number and type of junc- τ = c B c B (7) esc D (U /k T)2 tionpoints. Bycomparing2Dimagesofthefine-stranded t c B structure of the network at hourly intervals we identi- where D is a translational diffusion constant. We esti- fied discrete strand association and dissociation events t mate D from the short-time self diffusion constant in occurring over this period. Examples where the strand t a hard sphere suspension at the same φ, which since networkisrupturedareindicatedbythedashedcirclesin the dense regions of the gel have a volume fraction Fig. 9(a) while the solid circles identify new cross-links ≈ 0.55 is about 20% of the dilute free particle limit, formed by the reassociation of strands. Counting the D = k T/(6πη a). The limiting low shear viscos- number of reassociation N and rupture N events 0 B L link break ityη wasdeterminedbyextrapolatingmeasurementsof recorded per hour, as a function of the age of the gel, L the steady-shear rheology of the polymer solution to a results in the data shown in Fig. 9(b). There is gradual vanishing shear rate and fitting to the Martin equation, reductionovertimeinthenumberofreassociationevents N , as the network is formed in an open high-energy η link L =1+[η]c exp(k [η]c ) (8) state and then relaxes slowly into a lower more com- η p H p 0 pact structure. Strikingly however, we see that the rate of bond rupture does not show the same slowing-down. which has been found to correlate well viscosity in dilute N is essentially independent of age, presumably be- and semi-dilute polymer solutions (c /c∗ <10). Here [η] break p p causeruptureisanactivatedprocesswhichisdominated is the intrinsic viscosity, η is the viscosity of the mixed 0 by the single particle bond energy barrier. The conse- solvent, c the polymer mass concentration, and k is p H quence of the different time dependence seen for asso- a constant (equivalent to the Huggins constant at low ciation and rupture is that the proportion of breakage c ). Fitting data in the range c = 0.6 − 1.2 mg/ml p p eventsf =N /(N +N )(shownintheinsetof to Eq. 8 gave [η] = 2.32 ml/mg and k = 1.2. The break break link H Fig. 9(b)) grows with the age of the gel. The increasing width of the depletion zone δ and the potential at con- proportion of strand ruptures ultimately leads to failure tact −U /k T were estimated using the generalized free c B of the stress-bearing backbone of the gel and the initia- volume theory for mixtures of hard sphere colloids and tion of collapse. excluded-volumepolymerchains,asdetailedinRef.[17]. Figure 3(c) shows a comparison between the measured delay time τ and the average lifetime τ of a single d esc particle bond, estimated from Eq. 7. The ratio of the D. Appearance of structural heterogeneities two timescales is very nearly constant, for a wide range of polymer concentrations, with the delay time approxi- Work in the last decade [33, 34] has shown that mately 240 times the estimated single particle Kramers soft glassy materials frequently display structural het- 10 (a) (cid:84)(cid:87)(cid:0)(cid:29)(cid:0)(cid:20)(cid:23)(cid:0)(cid:88)(cid:17)(cid:16)(cid:19)(cid:0)(cid:83) (cid:84)(cid:87)(cid:0)(cid:29)(cid:0)(cid:23)(cid:22)(cid:0)(cid:88)(cid:17)(cid:16)(cid:19)(cid:0)(cid:83) (cid:84)(cid:87)(cid:0)(cid:29)(cid:0)(cid:17)(cid:16)(cid:20)(cid:0)(cid:88)(cid:17)(cid:16)(cid:19)(cid:0)(cid:83) (b) FIG. 9. (Color online). (a) 2D confocal images of coarsening gel network formed at φ=0.213, and c /c∗ =2.4. The particles p p areshowninwhite. Thesolidcirclesindicatenetworkjunctionswhichhaveformedinthepreceding3600s. Thedashedcircles indicate positions where the network has, in the same interval, broken. The scale bar is 30 µm long. Network collapse occurs at τd ∼120×103 s. (b) The number of reassociation Nlink and rupture Nbreak events per hour as a function of the age tw of the gel. The dashed lines are guides to the eye. The inset shows the tw-dependence of the fraction f of rupture events. erogeneities. In materials where the elastic behavior of was calculated from the static structure factor S(q,t ) w a material dominates over its viscous response any deformation due to a local rearrangement can propagate 1 (cid:90) (cid:68) (cid:69) S(q,t )= dq(cid:48) I˜(q(cid:48),t )I˜(−q(cid:48),t ) macroscopic distances so the size of regions which un- w 2πq∆q w w q≤|q(cid:48)|≤q+∆q dergo correlated rearrangements can be sizeable. If this (9) holdstrueinoursystem,thenitshouldbefeasibletosee where I˜(q,t ) is the two-dimensional Fourier-transform signsofthelong-rangedistortionfieldgeneratedbylocal w of the image intensity I(r,t ) at time t , ∆q = 2π/W, rearrangement events by microscopy. w w and W is the image width. The domain size is R = c (cid:82) (cid:82) π/(cid:104)q(cid:105) where (cid:104)q(cid:105) = dq qS(q)/ dqS(q). Measure- To test these ideas we have used confocal microscopy ments of R for different sample ages t are plotted in c w to monitor the time evolution of the network structure Fig. 10 and confirm that the aging of the gel network as a function of the vertical z-position within a gel. A shows considerable spatial diversity: the domain size is series of 2D-confocal images were collected at regularly- large in some regions of space and small in others. Im- spaced 1 mm heights from a colloid-polymer gel with a mediately after mixing, we observe the formation of a total height of h = 15 mm. Images were acquired for very uniform network with an average domain size of 0 ≈7hoursafterthecessationofmixing,untilthepointat (cid:104)R (cid:105) = 17.5 µm and a spatial variation of just 1.4% c which gel collapse occurred. The characteristic domain (standard deviation/(cid:104)R (cid:105)). But after t = 2 h, while c w size of the network R (h,t ) at a height h and time t the mean size has grown only slightly to (cid:104)R (cid:105)=21.3µm c w w c