Rotation of Giant Stars PDF
Preview Rotation of Giant Stars
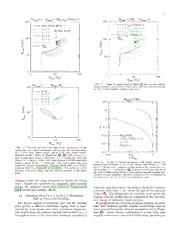
Draftversion June10,2015 PreprinttypesetusingLATEXstyleemulateapjv.5/2/11 ROTATION OF GIANT STARS Yevgeni Kissin DepartmentofAstronomyandAstrophysics,UniversityofToronto,50St. GeorgeSt.,Toronto,ONM5S3H4,Canada Christopher Thompson CanadianInstitute forTheoreticalAstrophysics,60St. GeorgeSt.,Toronto, ONM5H3H8,Canada Draft version June 10, 2015 5 1 ABSTRACT 0 The internal rotation of post-main sequence stars is investigated, in response to the convective 2 pumping of angular momentum toward the stellar core, combined with a tight magnetic coupling n between core and envelope. The spin evolution is calculated using model stars of initial mass 1, u 1.5 and 5M⊙, taking into account mass loss on the giant branches. We also include the deposition J of orbital angular momentum from a sub-stellar companion, as influenced by tidal drag along with 9 the excitation of orbital eccentricity by a fluctuating gravitational quadrupole moment. A range of angular velocity profiles Ω(r) is considered in the envelope, extending from solid rotationto constant ] specific angular momentum. We focus on the backreaction of the Coriolis force, and the threshold R for dynamoactionin the inner envelope. Quantitativeagreementwith measurementsof corerotation S in subgiants and post-He core flash stars by Kepler is obtained with a two-layer angular velocity . profile: uniform specific angular momentum where the Coriolis parameter Co≡Ωτ .1 (here τ h con con p is the convective time); and Ω(r) ∝ r−1 where Co & 1. The inner profile is interpreted in terms - of a balance between the Coriolis force and angular pressure gradients driven by radially extended o convective plumes. Inward angular momentum pumping reduces the surface rotation of subgiants, r and the need for a rejuvenated magnetic wind torque. The co-evolution of internal magnetic fields t s and rotation is considered in Kissin & Thompson, along with the breaking of the rotational coupling a between core and envelope due to heavy mass loss. [ Subject headings: stars: giants – stars: white dwarfs – stars: rotation – magnetic fields 3 v 7 1. INTRODUCTION the companion paper (Kissin & Thompson 2015, here- 1 afterPaperII)isthatonemustconsidertheco-evolution Measurementsofinternaloscillationmodesofredgiant 2 ofrotationandmagneticfieldsifoneistounderstandei- starsbytheKeplersatellitehavebeenusedtoinferrapid 7 ther. Thestrongflowofmaterialfromthe hydrogen-rich rotationintheradiativecore–insomecases,anorderof 0 envelope,throughburningshell(s), andintothe coreim- magnitude faster than at the surface (Beck et al. 2012; 1. Mosser et al. 2012). This evidence has been interpreted pliesthatonecannottreatcoreandenvelopeinisolation 0 by Cantiello et al. (2014) in terms ofa decoupling of the from each other. 5 rotation of the core from the convective envelope, which This observation leads us to discard models of the ro- 1 is assumed to rotate as a solid body. tation which neglect the influence of large-scale poloidal : magnetic fields that were deposited by previous convec- v Here we reconsider the role that convection plays in tive activity. For example, the Modules for Experiments i redistributing angular momentum within a star. So far X in Stellar Astrophysics (MESA) code (Paxton et al. only a limited understanding has been developed of the 2011)implementsaheuristicprescriptionforangularmo- r interaction between rotation and convection. The most a mentum redistribution in the radiative parts of a star, convincing theoreticalcalculations involvedirect numer- which starts with the current-driven (Tayler) instability ical simulations (e.g. Brun & Palacios 2009). of a predominantly toroidal magnetic field, leading to a Red giants offer a promising test case, because (i) the poloidalcomponentthatisthenwoundbackbydifferen- influence of the Coriolis force is reduced (although not tial rotation into the toroidal direction (Spruit 2002). entirely eliminated) in comparison with main sequence The nearly solid rotation of the Sun’s core has been (MS)stars;(ii)thegreatdepthoftheconvectiveenvelope used to infer the presence of a helical magnetic field reducesthe effect ofboundary conditions onthe angular (Gough & McIntyre 1998). The introduction of a per- velocity profile; and (iii) feedback from magnetic fields sistent twist to the field not only facilitates hydromag- on the rotation profile is less important, especially near neticstability(Braithwaite & Spruit2004),butalsosup- the tip of the red giant and asymptotic giant branches pressesdifferentialrotationacrosspoloidalmagneticflux (RGB and AGB), where most of the envelope rotates surfaces. The minimal poloidal field that will trans- slowly. Disentangling the mostimportantprocessesthat port angular momentum rapidly enough to compensate controlthe rotationprofileof a staris, for these reasons, changesinthecoremassprofileontheMSisonly∼10−6 easier in red giants than in the Sun. G; but a field ∼ 102-103 times stronger is required to The internalrotationof giantstarsalso hasimportant compensate a latitude-depenent convective stress that is implications for the magnetism and spin of their white partly transmitted through a tachocline layer into the dwarf(WD) remnants. Abasictheme ofthispaper,and 2 core(PaperII). The ascentofthe earlyredgiantbranch between the Coriolis and inertial forces. Both of these is completed over a Gyr, not a great deal shorter than prescriptions are compared against asteroseismic fits to thepresentageoftheSun,meaningthatasimilarlyweak Kepler data for subgiants and post-core He flash stars. poloidalmagneticfluxwouldenforcenearlysolidrotation We find that prescription i) provides a very promising in the core of a subgiant (e.g. Maeder & Meynet 2014). quantitative fit. Ina1-2M⊙ star,thesourceofthisfielddiffersbetween Measurements of surface rotation in subgiants pro- theearlyandlaterstagesofpost-MSexpansion. Theen- videindependentconstraintsontheinternalangularmo- velopeexpandsinmassduringthefirstdredge-upphase, mentum distribution in post-MS stars. Schrijver & Pols so that any remnant field in the outer core would have (1993) have used stellar models to argue for an inconsis- been deposited by a vigorously convective and rapidly tencybetweenthesesurfacemeasurementsandtheevolu- rotating envelope during the pre-MS contraction, when tion of ∼1.5M⊙ subgiants that maintain solid rotation. magneticfieldsseveralordersofmagnitudestrongerwere Adding a more rapidly rotating core, while maintaining present. Theminimalpoloidalmagneticfieldthatpushes solid rotation in the envelope, was found to have a neg- thecoretowardsolidrotationiswellbelowthethreshold ligble impact on the result. The discrepency between of detectability if transported to the surface of the star. modelsanddatawasthereforeinterpretedintermsofan Wenotethatourassumptionofsolidrotationinradiative additional magnetic wind torque acting on a star as it material depends on the relative weakness of additional develops a convective envelope upon leaving the MS. processesthat might sourcedifferentialrotation,such as Here we show that the same inward pumping of angu- thedampingofgravitywavesthatareexcitedinadjacent lar momentum in the envelope that reproduces the Ke- convective zones. pler observations also causes a factor ∼ 1/2 reduction We are led to a simpler model for the angular mo- in surface rotationspeed over the same interval,thereby mentum profile in a post-MS star: nearly solid rotation removing most (but not necessarily all) of the evidence in the core, as enforced by large-scale Maxwell stresses, for a magnetic wind torque. The calculations presented combinedwithinhomogeneousrotationintheconvective here, and in Paper II, neglect any rotational effect of envelope. The details of a dynamo operatingaroundthe surface magnetic fields during the post-MS phase. core-envelopeboundary,theensuingflowofmagnetiche- We also extend our considerations to the tip of the licity into the core, and the conditions under which the RGBandAGB.HeretheCoriolisforcehasareducedef- dynamo shuts off and core and envelope decouple, are fect,duetothegreaterexpansionofthestar(&10times addressed in Paper II. Here our focus is on the angular larger than the Kepler sample analyzed by Beck et al. velocity profile of the envelope, especially as it is influ- 2012 and Mosser et al. 2012). This leads us to consider enced by the Coriolis force. moreinwardlypeakedrotationprofilesthantheonesug- Convective Reynolds stresses appear to transport an- gested by fitting Kepler data. gularmomentuminwardinaccretionflows(Balbus et al. A final consideration is binary interaction. This is es- 1996). Thiseffectisdemonstratedinstarswithextended pecially important for stars which lose most of their na- convective envelopes by Brun & Palacios (2009) using talangularmomentumtoamagnetizedwindontheMS, three-dimensionalanelastic simulations. In slowly rotat- corresponding to an initial mass . 1.3M⊙. After such ing cases, most relevant to the present discussion, the a star ascends to the upper RGB or AGB, the inward specific angular momentum is found to be independent pumpingofangularmomentumcannot,byitself,sustain of radius. Co&1 in the convective envelope. Therotationfrequencyofthesolarconvectiveenvelope A robust hydromagnetic dynamo is maintained dur- is, by contrast, roughly independent of radius – a fact ing the greatest expansion of the star only if it encoun- thatappearstohaveinfluencedtreatmentsofrotationin ters an external source of angular momentum. We con- thepost-MSphase. Althoughthesolarenvelopealsocov- sider the interaction of a convecting giant with a com- ersmanyscaleheights,ithasamodestaspectratio(0.7:1 panionplanet,calculatingthecombinedorbitalevolution in radius), implying that thermal boundary conditions of the planet and the change in the angular momentum have a stronger influence on the rotation profile than in of the star. An interesting detail of this evolution is a star with a deep envelope (e.g. Browning et al. 2006). the excitation oforbitaleccentricityby the gravitational The Sun is not especially rapidly rotating by the stan- quadrupole associated with large-scaleconvective eddies dards of late-type MS stars, although the Coriolis force in the giant. In the case of a planetary companion, this still has a significant effect on its rotation profile. The effect is much more pronouncedthan when the compan- rotation period P = 2π/Ω is about 3 times the local ion is a neutron star (Phinney 1992), and we show that rot convective time τ = ℓ /v (where v is the speed it extends the range of orbital periods within which the con P con con of a convective eddy and ℓ the pressure scale height), planetgivesupitsorbitalangularmomentumtothestar. P corresponding to a Coriolis parameter Co ≡ Ωτ ∼ 2. con 1.1. Plan of the Paper Dynamo action may also influence the rotation profile (Brun et al. 2004). Weinvestigatetherotationprofileofadeepconvective The most important decision to be made here is how envelopeinSection2,withafocusonthebackreactionof to handle the backreaction of the Coriolis force on the the Coriolis force on angular momentum pumping. Var- inward pumping of angular momentum. We investigate ious angular velocity profiles are compared against the two simple prescriptions: i) a balance between the Cori- Kepler measurements of core rotation for subgiants and olis force and non-radial pressure gradient forces that post-He flash stars in Section 3. The effect of angular result from the entropy difference between convective momentumpumpingontheevolutionofsurfacerotation downflowsand upflows; and ii) an upper limit Co∼1 in of subgiants is examined in Section 3.2. the inner envelope,representinganapproximatebalance In Section 4, we consider the rotational evolution of 3 model stars of initial mass 1 and 5M⊙, including the ef- (e.g. Balbus 2009) fectsofconvectivepumping,angularmomentumlosstoa ∂Ω2 1 ∂P ∂S g(r)∂S wind,andplanetaryinteraction. Detailsoftheevolution rsinθ ≃− = . (1) of the orbit of a planet around an expanding giant are ∂z C ρr ∂r ∂θ C r ∂θ p p giveninSection5,includingdragfromthetideraisedon Here P and ρ are pressure and density, g(r) = thestarandtheexcitationofeccentricitybyaconvective GM(r)/r2 is gravity, and the specific entropy is S = quadrupole. Some outstanding questions are addressed in the con- [µ(γ − 1)]−1ln(P/ργ), approximatedhere as that of an cluding Section 6. The appendix gives further details of ideal gas with mean atomic weight µ and specific heat our calculation of eccentricity growth in the orbit of a Cp (Cv) at constant pressure (volume). companion planet. The ‘thermal wind’ approximation used in Equation (1) holds because |∂P/∂θ| ≪ |∂P/∂lnr|. In the up- per, slowly rotating part of the envelope, the latitudinal 2. PUMPINGOFANGULARMOMENTUMINDEEP pressuregradientissourcedbytheentropydifferencebe- CONVECTIVEENVELOPES:BACKREACTIONFROM THECORIOLISFORCE tween upflows and downflows,and is smaller by a factor (v /c )2 than the radialgradient. Our focus here is on The deep convective envelope of a giant star divides con s a rapidly rotating solution to Equation (1), where the into an outer part that is slowly rotating (Co . 1); and angular pressure gradient which sources ∂S/∂θ is pro- an inner part where Co & 1 and the rotation profile is influenced by the Coriolis force. portional to Ω2. The entire envelope may rotate slowly near maximum When the gravitating mass in the inner envelope is expansion, especially if the spin angular momentum of dominated by the stellar core, gravity g(r)∝r−2. From thestarhasbeenstronglydepletedbyamagnetizedwind Equation (1) we obtain the ansatz during the MS phase. On the other hand, a star is still −3 r compact enough during the early stages of post-MS ex- Ω2(r,θ)=Ω2(R ) f(cosθ). (2) c pansion that Ωτcon ≫1 throughout much of the convec- (cid:18)Rc(cid:19) tive envelope. Here R is the radius inside of which Co&1. We imagine that entropy is approximately conserved c One subtlety here is that the stellar mass profile is over downflows and upflows that are extended com- not as centrally concentrated during the early subgiant pared with a local scale height. Some indirect evidence expansion. This generally leads to a shallower scaling for such a configuration has long been obtained from of Ω with r: taking g(r) ∝ r−β, with β < 2, we find one-dimensional models of giant convection, which re- Ω(r)∝r−(1+β)/2. Afittothegravityprofileintheinner quire a mixing length exceeding a single scale height convective envelope over the range of expansion that is (Sackmann & Boothroyd 1991). probed by the Kepler asteroseismic data gives β ∼ 1, Such a suppression of radial mixing is suggestive corresponding to Ω(r) ∝ r−1. The monopolar scaling of an inwardly peaked rotation profile in the outer, of g is approached following the first dredge-up, and is slowly rotating envelope, corresponding to the conser- maintained near the tips of the RGB and AGB. vation of specific angular momentum j by individual WeimaginethattherotationprofileorganizesatCo≫ convective flows – as indeed is obtained numerically by 1intoaxiallysymmetricrolls. Inotherwords,thestrong Brun & Palacios (2009). Rotation profiles intermediate latitudinal dependence of the Coriolis force is hypothe- between Ω(r) ∝ r−2 and solid rotation could clearly be sized to translate into a persistent latitudinal entropy obtainedfromlimited mixing, butfor definiteness we fo- gradient. If, furthermore,the entropy is conservedalong cus here on the simple case ∂j/∂r → 0 where Co < 1. radiallyextendedconvectiveplumes,thenwecandecom- Obtaining the angular velocity profile in the inner enve- posetheentropyprofileintolow-ordersphericalharmon- lope depends on a more detailed analysis of the Coriolis ics, S(r,θ,φ)=S +δS P (cosθ). Substituting this into force, which we give below. 0 0 ℓ Equation (1) along with Equation (2), and normalizing We consider the evolving partition between fast and f =1 at θ =0, we get slow rotation in Section 3.1, and how it depends on the angular momentum retained (or gained) by the star in 21 1 f=1 (ℓ=2); f = cos2θ− (ℓ=4); Section 4. Given a flat distribution of specific angular 20 20 momentum in the outer envelope, an intermediate-mass 1 stargenerallysustainsaninner zonewhereCo&1,even f= 495cos4θ−234cos2θ+19 (ℓ=6). (3) 280 near the tip of the RGB or AGB; but a star which spins (cid:0) (cid:1) down on the MS must gain angular momentum from a Angular and radial gradients in Ω are generally com- planetary or stellar companion. parable in this type of flow (excepting the simplest case of a quadrupolar entropy pattern). We note that rota- tion is fastest at the pole for a given ℓ (corresponding 2.1. Extended Upflows and Downflows with to an‘anti-solar’rotationprofile), but thatthe opposing Quasi-Geostrophic Balance gradient can be obtained by superposing ℓ=2 with any When the inner zone with Co&1 covers a wide range higher harmonic. A small anti-rotation is also present of radius, we can look for a power-law scaling of the ro- in a narrow latitudinal band when the entropy follows a tationfrequency Ω withsphericalradius. Thestellaren- single spherical harmonic. velope is nearly adiabatic and spherically stratified. In AcaveathereinvolvesourneglectoftheLorentzforce, this inner zone of fast rotation (Ωrsinθ ≫ v ) about whichmayhaveaconsiderableinfluencenearthebound- con an axis zˆ (θ = 0), the steady vorticity equation reads aryofaconvectionzone,butdoesnotobviouslycompete 4 with the right-hand side of equation (1) within a deep Whenthestarhasmoreangularmomentum,wemain- convective layer. In particular, the magnetorotational tain the profile (7) in the outer part of the convection instability (MRI) is ineffective in the outer part of the zone, and consider envelope where Co < 1, because the growth time of a r −α MRI mode is longer than the convective time. (I) Ω¯(r)=Ω¯(R ) c (cid:18)R (cid:19) c 2.2. Rapid Mixing Between Upflows and Downflows Co r −α We now turn to consider the consequences of rapid = trans ; R <r <R benv c τ (R )(cid:18)R (cid:19) mixing between upflows and downflows for the rotation con c c profile in parts of the envelope that reach Co ∼ 1. This (9) provides a useful comparison with the results of Section in the inner envelope. Here Co = O(1). As the an- 2.1, and demonstrates how the radial angular velocity trans gular momentum increases R moves outward, and may gradientis tied to the presence of radiallyextended con- c reach the outer radius of the star, in which case Co is vective flows. We show that the downward advection of larger than unity everywhere in the envelope. angular momentum cannot push the flow to Co ≫ 1 in Followingthe abovediscussion, we will explorepower- the inner part of an extended envelope, where τ de- con law indices 1 < α < 3/2, with the preferred value de- creases inward. This result has a simple interpretation: pending on the radialscaling of gravity. Such a rotation the competition between the Coriolis force and the iner- profilecorrespondstotransportofenergybyradiallyex- tial force limits Co to a value of the order of unity. tended, adiabatic plumes. In the mixing length approximation, the entropy dif- Asecondprofile,basedonmixinglengththeory,is ob- ference between upflows and downflows is related to the tainedby setting Coto a constanteverywhereinside the speed of a convective eddy by (e.g. Bethe 1990) radius R , c δh C v2 δS = = p con. (4) (II) Ω¯(r)= Cotrans +Ω ; R <r <R . (10) k T C −C k T 0 benv c B p v B τ (r) con Here δh is the perturbationto specific enthalpy andT is The most important difference with profile I is that Co temperature. Then the angular entropy gradient can be remainspeggedat Co ∼1 inthe absenceofthe con- trans estimated as ∂S/∂θ ∼ (r/ℓP)δS. Because it turns out stant term. Setting Ω0 = 0 strictly limits the angular that Co = O(1), we cannot take Equation (1) literally, momentum which the envelope may contain, a bound butcanstilluseittoestimatethe magnitudeoftheshift which is easily violated during core helium burning. We of angular velocity across a scale height: also require that R is bounded above by the radius at c δ(Ω2)∼ g(r)vc2onµ = vcon 2. (5) wtiohnicohfτacolanyreerabcehleoswatmheapxhimotuomsp;htehriesipnrewvheincthsΩ¯thiencfroeramsaes- ℓP kBT (cid:18) ℓP (cid:19) outward. See Figure 1. We look for a rotation profile that diverges inward, so 2.4. Latitudinal Differential Rotation that the constant term in Ω can be neglected. Then we The latitudinal shift in rotation frequency (e.g. be- find v (r) tween pole and equator) has an important influence on con Ω(r)∼ . (6) the growth of magnetic helicity in the growing core of ℓ P an RGB or AGB star (Paper II). In rotation model Asadvertised,theCoriolisparameterdoesnotrisemuch I, where Co > 1 is maintained by radially extended above unity. (Faster rotation can, of course, still be ob- convective flows, we deduce a strong latitudinal shift: tained by superposing uniform rotation on the flow.) ∆Ω/Ω¯ ≡ (Ω −Ω )/Ω¯ ∼ 1. A strong shift is also eq pole For example, in a nearly adiabatic envelope with maintained in the mixing length approximation (rota- g(r) ∝ r−2, the speed of an eddy scales as vcon ∝ tion model II), as long as the envelope rotates rapidly (ρr2)−1/3. Then ρ(r) ∝ r−3/2 implies Ω(r) ∝ r−7/6 for enough to maintain Co ∼ 1 at the base of the enve- γ =5/3, which is shallower than the profile (2). lope. It is seen in the more rapidly rotating simulations of Brun & Palacios (2009). 2.3. Model Ω¯(r) Profiles We note that weakerlatitudinal differentialrotationis expected in a compact convective envelope with v ≪ Asimpleparameterizationoftherotationprofilewhich con incorporatestheselessonsmaybeconstructedasfollows. Ωrsinθ, as is encountered in the Sun, ∆Ω/Ω¯ ∝Co−2. Wherethe Coriolisforcecanbe neglected,atr >Rc, we 2.5. Matching of Rotation between consider a flat distribution of specific angular momen- Core and Convective Envelope tum, −2 Therotationofcoreandenvelopeareeasilycoupledto r Ω¯(r)=Ω¯(R ) ; r >R . (7) each other when the inner envelope retains enough an- c c (cid:18)Rc(cid:19) gular momentum to sustain a large-scale hydromagnetic Here Ω¯ is the angular velocity averaged over a spheri- dynamo. Thedetailsofthiscouplingdependonwhether the core grows, or recedes, as measured in the radial cal shell. If the angular momentum of the star is small enoughthat Ω¯(r)τ <1 throughoutthe envelope, then mass coordinate. When the core is growing, the instan- con taneous state of the dynamo is the main consideration, we identify R with the base of the envelope, c becausemagnetic fields thatareamplified nearthe core- R =R ; (Ωτ <1atR ). (8) envelope boundary are advected downward. When the c benv con benv 5 malpulsations,whicharepresentontheterminalAGB). Solidrotationis enforcedin the outer core during down- ward drift if the radial Alfv´en speed is larger than this drift speed. This requires that the large-scale poloidal magnetic field that is generatedin the inner envelope be strong enough that B2 (v −dR /dt)2 r & r benv . (11) 4πρ(R )v2 v2 benv con con We show in Figure 2 both the drift speed relative to the core-envelopeboundary, and the convective speed in the innerenvelope(asevaluatedusingmixing-lengththeory), during the post-MS evolution of a 1.5M⊙ model star. The same quantities arealso shownfor a 5M⊙ star near the tip of the AGB. (Further details of these models are described in Sections 3 and 4.) One sees that during the early subgiant expansion of the 1.5M⊙ model, the remnant poloidal magnetic field inthe outercoreneedonlyretainanenergydensity that exceeds ∼ 10−16 − 10−15 of the instantaneous convec- tive energy density in order to compensate changes in rotation induced by the evolving mass profile. Magnetic fields∼102-103timesstrongerareneededtocompensate a latitude-dependent convective stress (Paper II). The envelope decreases more rapidly in mass near the tip of the RGB and AGB, and the magnetic energy density that is self-consistently generated during these phasesmustrisetoabout∼10−8−10−6oftheconvective energy density. We conclude that magnetic decoupling of core from envelope is most easily achieved during the brief phase where the envelope is expelled. In Section 3 we concentrate on the comparison with Kepler asteroseismic data, which only covers post-MS stars more compact than ∼ 10R⊙. These subgiants and core He burning stars evolve on a relatively long timescale (∼ 102 times the duration of the thermally pulsating AGB phase). The results shown in Figure 2 strongly suggest that the rotation of core and envelope remain well coupled in these stars. Wethereforetakethecoretorotateasasolidwiththe mean rotation at the base of the envelope, Fig.1.—ExamplesofrotationmodelsI(toppanel)andII(bot- tom panel), both taken from the 5M⊙ model near the tip of the Ωcore =Ωbenv ≡Ω¯(Rbenv). (12) AGB.Each panel shows several rotationprofiles correspondingto differenttotalstellarangularmomenta. Themagentacurveshows, An explanation for the rotation behavior of the Kepler for reference, the profile of τcon(r). Black solid lines represent sample must be found in the redistribution of angular segments where Ω(r) ∝ r−2 and red dotted lines Ω(r) ∝ r−1. momentum within an extended convective envelope. Top panel: as J⋆ is increased, the transition radius Rc, forwhich Ctroeoam(cRhtecos)tto=hpe1rre,apmdreiousvesensotfmomuotadwxeailmrsduw.mitBhτocitnotncor,mewasepinabgneegJli:⋆n,pbtrouotfialdnedoswafrwoumhneinfboorRmtc- 3. COMPAWRIISTOHNKOEFPL1.E5RMD⊙AMTAODELSTAR Ω component (the lastterm inEquation (10)). This prevents the We beginby calibratingthe rotationmodels described formation of an outer zone of positive ∂Ω/∂r. Black curve: con- by Equations (7) and (9)-(12) against the core rotation stant j,reachingCo=1at thebase ofthe envelope; green curve: Ω(r) = vcon/ℓP; blue curves: constant Ω component that grows periods of 1 − 2M⊙ subgiants and post-core He flash with increasing J⋆. Kepler asteroseismic data favor model I over starsasmeasuredbyBeck et al.(2012)andMosser et al. modelII. (2012). For ease of comparison, we use the same stellar model as Cantiello et al. (2014), namely a 1.5M⊙ star ofsolarmetallicitywithzero-agemainsequence(ZAMS) core is receding in mass (as it does when a star first as- equatorial rotation speed 50 km s−1. cendsthegiantbranchduringthefirstdredge-upphase), Our calculation also employs the 1D stellar evolution thecouplingalsodependsonapriordynamoprocessthat codeMESA (Paxton et al.2011,version5527),butwith implanted a magnetic field in the core material. the built-in prescriptions for angular momentum trans- Akeyconsiderationisthemagnitudeofthedriftspeed port turned off. Instead, the rotationprofile is ‘patched’ v − dR /dt of stellar material with respect to the onto the sequence of stellar models. r benv core-envelopeboundary(averagedifnecessaryoverther- Thetotalspinangularmomentumofthestarisevolved 6 Fig.3.—Rotationperiodatthebaseoftheconvectiveenvelope, in a MZAMS = 1.5M⊙ model star, as a function of time during the RGB and early core He burning phases. Curves correspond to different rotation profiles. Black line: rotation period Pbenv corresponding to Cobenv =1 (with τcon evaluated in the mixing- length approximation). Green dashed line: solid rotation. Red dottedline: uniformspecificangularmomentum(evenwhereCo> 1). Bluelong-dashedline: rotationmodelIgivenbyEquations(7), (9)withα=1. Magentadashed-dottedline: rotationmodelIwith α = 3/2. Vertical black lines show the age range probed by the Keplersubgiantmeasurements,withcorrespondingstellarradius. profile I, as given by Equations (7), (9) with α = 1 (or 3/2). NowP sitsclosetotheobservedrangeof10−20 benv days. Thisperiodisidentifiedherewiththecorerotation period. Another important feature is the large jump in rota- tion period between the red giant and core He burning phases (Figure 4). The latter, slower, rotation results from a retraction of the convective envelope combined with continuing angular momentum pumping and core- envelope synchronization. (It was previously ascribed Fig.2.—Flowspeedofstellarmaterialwithrespecttothecore- by Cantiello et al. (2014) to the conservation of angu- envelope boundary, compared with convective speed in the inner lar momentum by an expanding core that has already envelope. Upper panel: 1.5M⊙ model from the early subgiant decoupled rotationally from the inner envelope.) expansion to the thermally pulsating AGB. Bottom panel: 5M⊙ Acloserlookattheeffectoftheinnerrotationindexα, modelatthetipoftheAGB.Thelogarithmicabscissaintheupper panel is referenced to the time tTAGB of envelope ejection. The and the initial rotation speed of the star, is provided by timecoordinateinthelowerpanelhasbeenshiftedtofocusonthe Figures 4 and 5. Here one sees that an index α around finalfewhundredyears. 1−1.1 provides a close agreementwith the Kepler mea- surements for stars more massive than ∼1.3M⊙. There issomedegeneracybetweentheeffectsofchangingαand self-consistently in response to mass loss, using the pre- initial rotation speed. It is interesting to note that this scriptiondescribedinSection4.1. Magneticwindtorques profile agrees well with the analytic scaling derived for are neglected, for the reasons described in Section 3.2. rotation model I in Section 2.1 in the case (appropri- The net effect of mass loss is found to be modest up to ate to the expansion phase probed by the Kepler data) the onset of core He burning: a factor ∼ 2 reduction in where g(r)∝r−1 in the inner envelope. Recall that this angular momentum during the RGB phase. rotationmodel represents radially extended upflows and WeobservefromFigure3thattheinnerenvelopemust downflows in a geometrically deep, adiabatic envelope. rotate rapidly (Co >1), even in the case of solid ro- A different conclusion emerges for stars close to so- benv tation,overtherangeofexpansionprobedbytheKepler lar mass. We see in the bottom panel of Figure 4 that data. The rotation period Pbenv =2π/Ωbenv at the base the core of a 1M⊙ star without a close planetary com- of the envelope would actually decrease with increasing panion is predicted to spin ∼ 5−10 times more slowly expansion if the entire envelope could sustain a profile during subgiant expansion than is seen in our 1.5M⊙ Ω(r)∝r−2. model. On the other hand, the core rotation during the This effect is still present in the less peaked rotation He burning phase is only ∼ 3 times slower, and indeed 7 Fig.5.— Same as upper panel of Figure 4, but now for various initialrotationspeedsofthe1.5M⊙star,andtwoselectedscalings forΩ(r)intherapidlyrotatinginnerzone. Fig. 4.—Rotationperiodatthebaseoftheconvectiveenvelope during the early giant expansion and the core He burning phase of a 1.5M⊙ star (upper panel) and a 1 M⊙ star (lower panel). Rotation model I given by Equations (7), (9) with Cotrans = 1 and varying inner index α (here Ω(r)∝r−α insidethe radius Rc whereCo=Cotrans). The1.5M⊙ starisgivenaZAMSequatorial rroottaattiioonnaslpaenegdu5la0rkmmoms−e1n,tuwmh.ileDtihaego1naMl⊙blasctakrliinseg:ivfietnttohKeesopllearr phFaisges.6o.f—thePervoofilluetioofnCoofroioulris1p.5aMram⊙emteordwelitwhitrhadiniuitsiadluvrriontg=tw50o subgiant data from Cantielloetal. (2014). The radius at which kms−1. Blackcurve: subgiant(stellarradius6R⊙)withinnerro- majority of helium clump stars are found is marked in the upper tationindexα=1inEquation(9). Coloredcurves: nearthetipof panel. theAGB(stellarradius100R⊙)withuniformspecificangularmo- mentuminouterenvelope,andinnerrotationprofilecorresponding toeitherα=1or1.5,ortoCosaturatingatunity. remains within the range measured by Kepler for clump stars. Significant spindown by magnetic wind torques during the subgiant phase (van Saders & Pinsonneault relativelythinlayerbelowthesurface. IndeedCoreaches 2013) would have similar effects. aconsiderablevalue∼10−30atthebaseoftheenvelope (Figure 6). The measured core rotation rates probe the 3.1. Transition from Co&1 to Co.1 throughout angular velocity profile that is sustained in the envelope Bulk of Convective Envelope in a regime of relatively rapid rotation. The Kepler sample of subgiants and core He burning Figure7showstheevolvingpartitionbetweenanouter stars probes a different rotational regime than is expe- zone with uniform specific angular momentum, and an rienced by most giants near their maximum expansion. innerzonewithangularvelocityparameterizedbyEqua- TheKeplerstarsarecompactenoughthatwefindCo&1 tion (9). These curves correspond to a star with spin throughoutmost of the convectiveenvelope, excepting a angularmomentum close to its birth value, assuming an 8 Fig.8.—Greencrosses: observedsurfacerotationspeedsofclass IVstarsfromSchrijver&Pols(1993),multipliedby4/πtoaccount forunknowninclination,asafunctionofeffectivetemperature. We show for comparison our model of a 1.5M⊙ star on the early red giant branch, with initial rotation speed 50 km s−1. Curves cor- respondtodifferent profilesof rotationintheenvelope, combined with solid rotation in the core. Solid rotation is enforced in the envelopewhentheaspectratioRbenv/R⋆ betweenthebaseofthe envelope and stellar photosphere is larger than 0.9 or 0.5. The α=1,1.5curvescorrespondtorotationmodelI.Inthecaseα=1 (whichbestreproducestheasteroseismicfitstoKeplerdata)there is a factor ∼ 1/2 reduction in surface rotation compared with a solidrotatoratlog(Teff)<3.8. 3.2. Surface Rotation of Subgiants: Angular Momentum Pumping Versus Magnetized Winds The expansion of a star following the MS phase is associated with a drop in surface rotation. The strength of this drop is sensitive to the distribution of angular momentum within the star, as well as to external torques associated with magnetic activity in the deepening envelope. Schrijver & Pols (1993) and Fig. 7.— Profile of convective envelope during RGB expansion van Saders & Pinsonneault (2013) have presented evi- (toppanel)andAGBexpansion(bottom panel)inrotationmodel dence for an inconsistency between solid rotation in the I. As the aspect ratioof stellar radiusto the base of the envelope envelope and measurements in the surface rotation of mgraorwkss,tthhee tdroamnsaiitniownitphoiinntwbheictwheCeno &an1oushterirnkzos.neTwheithraudniuifsorRmc 1.5−2M⊙stars: themeasuredrotationisafactor∼2−3 specific angular momentum, and an inner zone with Ω(r)∝r−α. slower than is expected for constant stellar angular mo- Thistransitiondependsonlyweaklyontheinnerindexα,because mentum. mostoftheangularmomentumisstoredintheouterenvelope. A similar effect would be imposed by inward pump- ingofangularmomentum. Schrijver & Pols(1993)show equatorialsurface rotationspeedof 50kms−1. Outto a thatafast-spinningcorehasanegligibleeffectonthere- sult if the convective envelope maintains solid rotation, stellarradiusR⋆ ∼10R⊙,theenveloperemainscompact but did not consider envelopes with inward-peaked ro- enough that log(R /R ) . log(R /R ). Beyond this ⋆ c c benv tation profiles. The key point here is that the radiative size, the inner rotation rate is controlled by the rotation core becomes very compact early in the expansion onto profile at Co.1. the red giant branch, in the sense that its moment of The spin and magnetization of the WD remnant, as inertia is a very small fraction of M R2 . There- exploredinPaperII,arestronglyinfluenced bythe Ω(r) benv benv fore inhomogeneous rotationin the envelope has a much profile of a slowly rotating convective envelope near the largereffectonsurfacerotationthandoesafast-spinning tipoftheRGBandAGB.Thenthegravityprofilesteep- core. ensintheinnerenvelope,andwemaintainconsideration We show in Figure 8 the evolution of the surface ro- of rotation profiles at Co>1 that are somewhatsteeper than suggested by the fit to Kepler data: α ∼ 3/2 as tation in our 1.5M⊙ model, for the same set of inho- mogeneous rotation profiles that we have previously ex- opposed to α∼1 in Equation (9). plored. The envelope at high T is still relatively thin. eff Wethereforeimpose∂Ω/∂r=0,tomimicthesolarrota- 9 tion profile, when the aspect ratio R /R rises above benv ⋆ a critical value 0.5 or 0.9. The profile that is favored by the Kepler core rotation data, Equations (7) and (9) withinnerindexα=1,showsafactor∼1/2reductionin surface rotation compared with the solid rotator. This removes a significant part of the discrepency found by Schrijver & Pols (1993) and van Saders & Pinsonneault (2013), but perhaps not all. 4. EVOLVINGROTATIONPROFILEWITHMASSLOSS ANDINTERACTIONWITHAPLANET Wenowconsidertherotationalevolutionofastarasit approachesthetipoftheRGBandAGB.Heretheprob- ability of interacting with a companion increases signif- icantly. The Coriolis parameter also drops markedly at the base of the convective envelope. We maintain our focus on a two-layeredrotation model. Twotestcasesareanalyzedindetail: astarwithinitial mass MZAMS = 1M⊙, which experiences strong spin- down on the MS and interacts with a planet; and an intermediate-mass star (MZAMS =5M⊙) which remains staFrigd.u9ri.n—gREGvoBlu,tcioonreoHfespbiunrnainnggulaanrdmfionmalenAtGumB pofha1sMes.⊙Cmuorvdeesl rapidly rotating at the end of the MS and leaves behind represent cases described in the text. Red lines (JMS): no exter- a massive WD. This second stellar model is also allowed nal source of angular momentum. Black lines (JJupiter,ai=1AU): to interact with a companion. MESA is used to evolve absorption of a Jupiter-mass planet orbiting initially at ai = 1 AU. Short dashed lines (Ω = c): solid rotation throughout core these stellar models (both of solar metallicity) from the andenvelope. Otherlinescorrespondtotwo-layerrotationmodel, ZAMS to the post-AGB phase. with uniform specific angular momentum in outer envelope, and In the case of the solar-massstar,the interactionwith varying inner rotation profile. Solid (long-dashed) curves: α = 1 a planet was followed from the base of the RGB, when (α= 1.5) in Equation (9); long-dashed-dotted curve: profile (10) withCo=1ininnerzone. the star has expanded to a radius R⋆ ∼ 10.9R⊙ (age t ∼ 12.37 Gyr). At that point, the spin angular mo- 10.9 mentumwassetequaltothatofthepresentSun. Stellar quantities at times intermediate between the outputed with η =0.5. Here (˜) denotes stellar parameters mea- R MESAmodelswereobtainedbylinearinterpolation. De- sured in solar units. On the AGB we use tails of the orbital integration and the interaction be- twTeehnepelqaunaettoarinadl rsotatartaiorne pspreeseedntoefdtihneS5eMcti⊙onst5a.r is set M˙⋆Bloecker =1.93×10−21ηBL˜M⋆3˜.73R.˜1⋆ M⊙ yr−1 (15) to 50 km s−1 at the ZAMS, corresponding to the peak ⋆ in the measured vsini distribution (Wolff et al. 2007). from Blo¨cker (1995). Mass loss according to the Blo¨cker Both the 1M⊙ and 5M⊙ models are taken to rotate formula is turned on when the central H and He abun- as a solid body on the MS. Deviations from solid body dances are less than 10−2 and 10−4, respectively. rotationdevelopaftertheformationofadeepconvective The choice of AGB mass loss parameter ηB is moti- envelope, following the approach of Section 2. vatedbyrecentclusterdata(e.g. Dobbie et al.2009). As There are instances around the tip of the AGB when we discuss further in Paper II, we set ηB = 0.05, corre- the outer envelope splits into several convection zones, spondingto a finalWD massMWD ∼0.87M⊙ (fromthe separated by radiative layers. The entropy gradient in 5M⊙ progenitor). The same wind parameters are used these radiative zones, although positive, remains small. forboththe1M⊙ and5M⊙ models. Thesolar-typestar We impose a matching of specific angular momentum loses ∼ 0.25M⊙ on the RGB and another ∼ 0.21M⊙ on across them. the AGB for a final WD mass MWD ∼0.54M⊙. 4.2. Rotation Rate of the Inner Envelope and Core 4.1. Loss of Angular Momentum on the RGB and AGB There is a simple relation between spin angular mo- Magnetic wind braking is not taken into account in mentum and core angular velocity Ω when the enve- our simulations during the subgiant or giant phases, for benv lopeisextendedandmaintainsuniformangularmomen- the reasons given in Section 3.2. Then the ejected mass tum per unit mass, carriesthespecificangularmomentumofthestellarpho- tosphere, dJ(r) 2 j(r)≡ = r2Ω¯(r)=const. (16) J˙ = 2Ω¯(R )R2M˙ . (13) dM(r) 3 ⋆ 3 ⋆ ⋆ ⋆ Given a net stellar angular momentum J , and an effec- ⋆ The rate of mass loss on the RGB is handled using the tive moment of inertia in the convective envelope, prescription of Reimers (1975), 2 2 I = 4πr2R2 ρ(r)dr = R2 (M −M ), L˜ R˜ eff 3Z benv 3 benv ⋆ benv M˙⋆Reimers =4×10−13ηR M⋆˜ ⋆ M⊙ yr−1, (14) (17) ⋆ 10 Fig.10.— Evolution of the Coriolis parameter at the base of Fig. 11.—Effect onthe5M⊙ modelstaroftheengulfmentofa the convective envelope. Curves correspond to those in Figure 9. substellarcompanionofmass(3,10,30,100)MJupiter fromaninitial UpperpanelshowstheRGB,coreheliumburningphase,andAGB. orbitai=2AU.Orbitalangularmomentumofplanetisaddedto Lower panel shows an expanded view of the tip of the RGB and starwhenitreachesaradiusR⋆=200R⊙ ontheAGB,asguided by more detailed tidal evolution calculations. The physical con- thebeginningofthecoreHeburningphase. sequences depend weakly on the epoch of engulfment, ifit occurs beforethefirstthermalpulse(att∼1.0717×108 years),whenthe envelopedynamobeginstocontributetothemagneticfieldofthe we obtain hydrogen-depletedcore. Upperpanel: timeevolutionoftransition J⋆ radius Rc between outer slowlyrotating zone (Co<1) and inner Ωbenv = I +I . (18) rapidlyrotating zone (Co>1). Bottom panel: change in Cobenv eff core duetotheaddedangularmomentum. Rotationprofilecorresponds Excepting near the point where the envelope has been to α= 1 in Equation (9). Although Rc increases with increasing ejected at the end of the AGB, the moment of inertia of angularmomentum, Cobenv decreases. the core can generally be neglected, I ≪I . core eff Theangularmomentumstoredinthecoreisenhanced byafactor∼(R /R )2,ascomparedwiththe caseof rotation profile is either described by a two-layer model ⋆ benv solid rotation throughout the star. This simple rotation (Section4.2)duringits post-MSevolution(‘j =c’inthe model breaks down when it predicts Co&1 at the base outer envelope, with various inner Ω(r) profiles); or it is of the convective envelope, and we employ the modified assumedtobesolid-bodyfromtheZAMStotheterminal rotation profiles (9), (10). AGB (‘Ω=c’). Considering first the 1M⊙ model, we compare several Figure 9 shows the evolution of J⋆. We see that solid- scenarios. The star is either assumed to evolve in isola- body rotation leads to a significant loss of angular mo- tion;ortointeractwithaJupiter-massplanetthatstarts mentum through the RGB winds, because little angular in a circularorbitof semi-majoraxis 1 AU. The internal momentum is stored deep in the star. Introducing an
