Review of analytic geometry

11 Pages·0.286 MB·English

by  Stewart J.

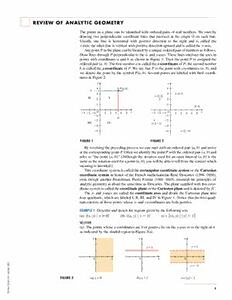
REVIEW OF ANALYTIC GEOMETRY
The points in a plane can be identified with ordered pairs of real numbers. We start by
drawing two perpendicular coordinate lines that intersect at the origin O on each line.
Usually one line is horizontal with positive direction to the right and is called the
x-axis; the other line is vertical with positive direction upward and is called the y-axis.
Any point Pin the plane can be located by a unique ordered pair of numbers as follows.
Draw lines through Pperpendicular to the x- and y-axes. These lines intersect the axes in
points with coordinates a and b as shown in Figure 1. Then the point P is assigned the
ordered pair (cid:1)a, b(cid:2). The first number ais called the x-coordinateof P; the second number
b is called the y-coordinate of P. We say that P is the point with coordinates (cid:1)a, b(cid:2), and
we denote the point by the symbol P(cid:1)a, b(cid:2). Several points are labeled with their coordi-
nates in Figure 2.
y y
4 P(a, b) 4
b
3 3 (1, 3)
(_2, 2)
II I
2 2
1 1
(5, 0)
_3 _2 _1O 1 2 3 4 5 x _3 _2 _1 0 1 2 3 4 5 x
_1 _1
a
_2 _2
III IV (_3, _2))
_3 _3
_4 _4 (2, _4)
FIGURE 1 FIGURE 2
By reversing the preceding process we can start with an ordered pair (cid:1)a, b(cid:2) and arrive
at the corresponding point P. Often we identify the point Pwith the ordered pair (cid:1)a, b(cid:2)and
refer to “the point (cid:1)a, b(cid:2).” [Although the notation used for an open interval (cid:1)a, b(cid:2) is the
same as the notation used for a point (cid:1)a, b(cid:2),you will be able to tell from the context which
meaning is intended.]
This coordinate system is called the rectangular coordinate systemor the Cartesian
coordinate system in honor of the French mathematician René Descartes (1596–1650),
even though another Frenchman, Pierre Fermat (1601–1665), invented the principles of
analytic geometry at about the same time as Descartes. The plane supplied with this coor-
dinatesystemiscalledthecoordinateplaneortheCartesianplaneandisdenotedby(cid:1)2.
The x- and y-axes are called the coordinate axes and divide the Cartesian plane into
four quadrants,which are labeled I,II,III,and IV in Figure 1. Notice that the first quad-
rant consists of those points whose x- and y-coordinates are both positive.
EXAMPLE 1 Describe and sketch the regions given by the following sets.
(a) (cid:4)(cid:1)x, y(cid:2) (cid:3) x(cid:3)0(cid:5) (b) (cid:4)(cid:1)x, y(cid:2) (cid:3) y(cid:1)1(cid:5) (c) {(cid:1)x, y(cid:2)(cid:3)(cid:3)y(cid:3)(cid:2)1}
SOLUTION
(a) The points whose x-coordinates are 0 or positive lie on the y-axis or to the right of it
as indicated by the shaded region in Figure 3(a).
y y y
y=1 y=1
0 x 0 x 0 x
2007 y=_1
copyright
Brooks-Cole FIGURE 3 (a) x (cid:1)0 (b) y=1 (c) |y|<1
mson 1
Tho
2 ■ REVIEW OF ANALYTIC GEOMETRY
(b) The set of all points with y-coordinate 1 is a horizontal line one unit above the x-axis
[see Figure 3(b)].
(c) Recall from Review of Algebrathat
(cid:3) (cid:3)
y (cid:2)1 if and only if (cid:4)1(cid:2)y(cid:2)1
The given region consists of those points in the plane whose y-coordinates lie between
(cid:4)1and 1. Thus,the region consists of all points that lie between (but not on) the hori-
zontal lines y(cid:1)1and y(cid:1)(cid:4)1. [These lines are shown as dashed lines in Figure 3(c) to
indicate that the points on these lines don’t lie in the set.]
y
Recall from Review of Algebrathat the distance between points aand bon a number line
(cid:3) (cid:3) (cid:3) (cid:3)
fi P™(¤, fi) is a(cid:4)b (cid:1) b(cid:4)a . T(cid:3)hus, the(cid:3) distance between points P1(cid:1)x1, y1(cid:2) and P3(cid:1)x2, y1(cid:2) on a
horizontal line must be x (cid:4)x and the distance between P (cid:1)x , y (cid:2) and P (cid:1)x , y (cid:2) on
|fi-›| a vertical line must be (cid:3)y (cid:4)2 y (cid:3).1 (See Figure 4.) 2 2 2 3 2 1
P¡(⁄, ›) (cid:3) 2 (cid:3)1
› To find the distance P P between any two points P(cid:1)x , y (cid:2)and P (cid:1)x , y (cid:2),we note
|¤-⁄| P£(¤, ›) 1 2 1 1 1 2 2 2
that triangle PP P in Figure 4 is a right triangle,and so by the Pythagorean
1 2 3
0 ⁄ ¤ x Theorem we have
(cid:3) (cid:3) (cid:3) (cid:3) (cid:3) (cid:3) (cid:3) (cid:3) (cid:3) (cid:3)
P P (cid:1)s P P 2(cid:5) P P 2 (cid:1)s x (cid:4)x 2(cid:5) y (cid:4)y 2
FIGURE 4 1 2 1 3 2 3 2 1 2 1
(cid:1)s(cid:1)x (cid:4)x (cid:2)2(cid:5)(cid:1)y (cid:4)y (cid:2)2
2 1 2 1
Distance Formula The distance between the points P1(cid:1)x1, y1(cid:2)and P2(cid:1)x2, y2(cid:2)is
(cid:3) (cid:3)
P P (cid:1)s(cid:1)x (cid:4)x (cid:2)2 (cid:5)(cid:1)y (cid:4)y (cid:2)2
1 2 2 1 2 1
For instance,the distance between (cid:1)1, (cid:4)2(cid:2)and (cid:1)5, 3(cid:2)is
s(cid:1)5(cid:4)1(cid:2)2(cid:5)(cid:6)3(cid:4)(cid:1)(cid:4)2(cid:2)(cid:7)2 (cid:1)s42(cid:5)52 (cid:1)s41
CIRCLES
y
An equation of a curve is an equation satisfied by the coordinates of the points on the
curve and by no other points. Let’s use the distance formula to find the equation of a cir-
P(x, y)
r cle with radius r and center (cid:1)h, k(cid:2). By definition, the circle is the set of all points P(cid:1)x, y(cid:2)
whose distance from the center C(cid:1)h, k(cid:2)is r. (See Figure 5.) Thus,Pis on the circle if and
(cid:3) (cid:3)
C(h, k) only if PC (cid:1)r. From the distance formula,we have
s(cid:1)x(cid:4)h(cid:2)2(cid:5)(cid:1)y(cid:4)k(cid:2)2 (cid:1)r
or equivalently,squaring both sides,we get
0 x
(cid:1)x(cid:4)h(cid:2)2(cid:5)(y(cid:4)k(cid:2)2(cid:1)r2
FIGURE 5
This is the desired equation.
Equation of a Circle An equation of the circle with center (cid:1)h, k(cid:2)and radius ris
(cid:1)x(cid:4)h(cid:2)2(cid:5)(y(cid:4)k(cid:2)2(cid:1)r2
In particular,if the center is the origin (cid:1)0, 0(cid:2),the equation is
x2(cid:5)y2(cid:1)r2
2007
copyright For instance,an equation of the circle with radius 3 and center (cid:1)2, (cid:4)5(cid:2)is
Brooks-Cole (cid:1)x(cid:4)2(cid:2)2(cid:5)(y(cid:5)5(cid:2)2(cid:1)9
mson
Tho
REVIEW OF ANALYTIC GEOMETRY ■ 3
EXAMPLE 2 Sketch the graph of the equation x2(cid:5)y2(cid:5)2x(cid:4)6y(cid:5)7(cid:1)0by first show-
ing that it represents a circle and then finding its center and radius.
SOLUTION We first group the x-terms and y-terms as follows:
y (cid:1)x2(cid:5)2x(cid:2)(cid:5)(y2(cid:4)6y(cid:2)(cid:1)(cid:4)7
Then we complete the square within each grouping,adding the appropriate constants
(_1, 3) (the squares of half the coefficients of xand y) to both sides of the
equation:
(cid:1)x2(cid:5)2x(cid:5)1(cid:2)(cid:5)(y2(cid:4)6y(cid:5)9(cid:2)(cid:1)(cid:4)7(cid:5)1(cid:5)9
or (cid:1)x(cid:5)1(cid:2)2(cid:5)(y(cid:4)3(cid:2)2(cid:1)3
0 1 x
Comparing this equation with the standard equation of a circle,we see that h(cid:1)(cid:4)1,
FIGURE 6
k(cid:1)3,and r(cid:1)s3,so the given equation represents a circle with center (cid:1)(cid:4)1, 3(cid:2)and
≈+¥+2x-6y+7=0
radius s3. It is sketched in Figure 6.
LINES
To find the equation of a line Lwe use its slope,which is a measure of the steepness of the
line.
Definition The slopeof a nonvertical line that passes through the points P(cid:1)x , y (cid:2)
1 1 1
and P (cid:1)x , y (cid:2)is
2 2 2
y L (cid:6)y y (cid:4)y
m(cid:1) (cid:1) 2 1
P™(x™, y™) (cid:6)x x2(cid:4)x1
Îy=fi-› The slope of a vertical line is not defined.
P¡(x¡, y¡) =rise
Îx=¤-⁄
Thus the slope of a line is the ratio of the change in y,(cid:6)y,to the change in x,(cid:6)x. (See
=run
Figure 7.) The slope is therefore the rate of change of ywith respect to x. The fact that the
0 x
line is straight means that the rate of change is constant.
Figure 8 shows several lines labeled with their slopes. Notice that lines with positive
FIGURE 7
slope slant upward to the right, whereas lines with negative slope slant downward to the
right. Notice also that the steepest lines are the ones for which the absolute value of the
y slope is largest,and a horizontal line has slope 0.
m=5
m=2 Now let’s find an equation of the line that passes through a given point P1(cid:1)x1, y1(cid:2) and
m=1 has slope m. A point P(cid:1)x, y(cid:2)with x(cid:2)x lies on this line if and only if the slope of the line
1
m=1 through P and Pis equal to m; that is,
2 1
y(cid:4)y
1 (cid:1)m
m=0 x(cid:4)x1
m=_1 This equation can be rewritten in the form
2
0 m=_1 x
y(cid:4)y (cid:1)m(cid:1)x(cid:4)x (cid:2)
m=_2 1 1
m=_5
and we observe that this equation is also satisfied when x(cid:1)x and y(cid:1)y . Therefore,it is
1 1
FIGURE 8
an equation of the given line.
2007 Point-Slope Form of the Equation of a Line An equation of the line passing through the
Brooks-Cole copyright point P1(cid:1)x1, y1(cid:2)and having slopey m(cid:4)iys1(cid:1)m(cid:1)x(cid:4)x1(cid:2)
mson
Tho
4 ■ REVIEW OF ANALYTIC GEOMETRY
EXAMPLE 3 Find an equation of the line through the points (cid:1)(cid:4)1, 2(cid:2)and (cid:1)3, (cid:4)4(cid:2).
SOLUTION The slope of the line is
(cid:4)4(cid:4)2 3
m(cid:1) (cid:1)(cid:4)
3(cid:4)(cid:1)(cid:4)1(cid:2) 2
Using the point-slope form with x (cid:1)(cid:4)1and y (cid:1)2,we obtain
1 1
y(cid:4)2(cid:1)(cid:4)3(cid:1)x(cid:5)1(cid:2)
2
which simplifies to 3x(cid:5)2y(cid:1)1
y Suppose a nonvertical line has slope mand y-intercept b. (See Figure 9.) This meansit
intersects the y-axis at the point (cid:1)0, b(cid:2),so the point-slope form of the equation of the line,
b with x (cid:1)0and y (cid:1)b,becomes
y=mx+b 1 1
y(cid:4)b(cid:1)m(cid:1)x(cid:4)0(cid:2)
0 x This simplifies as follows.
FIGURE 9
Slope-Intercept Form of the Equation of a Line An equation of the line with slope mand
y-intercept bis
y(cid:1)mx (cid:5)b
y In particular,if a line is horizontal,its slope is m(cid:1)0,so its equation is y(cid:1)b,where
y=b bis the y-intercept (see Figure 10). A vertical line does not have a slope,but we can write
its equation as x(cid:1)a, where a is the x-intercept, because the x-coordinate of every point
b
on the line is a.
x=a
0 a x EXAMPLE 4 Graph the inequality x(cid:5)2y(cid:7)5.
(cid:3)
SOLUTION We are asked to sketch the graph of the set (cid:4)(cid:1)x, y(cid:2) x(cid:5)2y(cid:7)5(cid:5)and we begin
FIGURE 10 by solving the inequality for y:
x(cid:5)2y(cid:7)5
y 2y(cid:7)(cid:4)x(cid:5)5
2.5 y(cid:7)(cid:4)1x(cid:5)5
2 2
y
=_ 2   1 x+25 Compare this inequality with the equation y(cid:1)(cid:4)12x(cid:5)52,which represents a line with
0 5 x slope (cid:4)12 and y-intercept 52. We see that the given graph consists of points whose y-coor-
dinates are largerthan those on the line y(cid:1)(cid:4)1x(cid:5)5. Thus,the graph is the region that
2 2
FIGURE 11 lies abovethe line,as illustrated in Figure 11.
PARALLEL AND PERPENDICULAR LINES
Slopes can be used to show that lines are parallel or perpendicular. The following facts are
2007 proved,for instance,in Precalculus:Mathematics for Calculus,Fifth Editionby Stewart,
copyright Redlin,and Watson (Thomson Brooks/Cole,Belmont,CA,2006).
Brooks-Cole
mson
Tho
REVIEW OF ANALYTIC GEOMETRY ■ 5
Parallel and Perpendicular Lines
1. Two nonvertical lines are parallel if and only if they have the same slope.
2. Two lines with slopes m1and m2are perpendicular if and only if m1m2(cid:1)(cid:4)1;
that is,their slopes are negative reciprocals:
1
m (cid:1)(cid:4)
2 m
1
EXAMPLE 5 Find an equation of the line through the point (cid:1)5, 2(cid:2)that is parallel to the line
4x(cid:5)6y(cid:5)5(cid:1)0.
SOLUTION The given line can be written in the form
y(cid:1)(cid:4)2x(cid:4)5
3 6
which is in slope-intercept form with m(cid:1)(cid:4)2. Parallel lines have the same slope,so the
3
required line has slope (cid:4)2and its equation in point-slope form is
3
y(cid:4)2(cid:1)(cid:4)2(cid:1)x(cid:4)5(cid:2)
3
We can write this equation as 2x(cid:5)3y(cid:1)16.
EXAMPLE 6 Show that the lines 2x(cid:5)3y(cid:1)1and 6x(cid:4)4y(cid:4)1(cid:1)0are perpendicular.
SOLUTION The equations can be written as
y(cid:1)(cid:4)2x(cid:5)1 and y(cid:1)3x(cid:4)1
3 3 2 4
from which we see that the slopes are
m (cid:1)(cid:4)2 and m (cid:1)3
1 3 2 2
Since mm (cid:1)(cid:4)1,the lines are perpendicular.
1 2
EXERCISES
11–24 Find an equation of the line that satisfies the given
A Click here for answers. S Click here for solutions.
conditions.
11. Through (cid:1)2, (cid:4)3(cid:2),slope 6
1–2 Find the distance between the points.
1. (cid:1)1, 1(cid:2), (cid:1)4, 5(cid:2) 2. (cid:1)1, (cid:4)3(cid:2), (cid:1)5, 7(cid:2) 12. Through (cid:1)(cid:4)3, (cid:4)5(cid:2),slope (cid:4)72
13. Through (cid:1)2, 1(cid:2)and (cid:1)1, 6(cid:2)
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
3–4 Find the slope of the line through Pand Q. 14. Through (cid:1)(cid:4)1, (cid:4)2(cid:2)and (cid:1)4, 3(cid:2)
3. P(cid:1)(cid:4)3, 3(cid:2), Q(cid:1)(cid:4)1, (cid:4)6(cid:2) 4. P(cid:1)(cid:4)1, (cid:4)4(cid:2), Q(cid:1)6, 0(cid:2) 15. Slope 3,y-intercept (cid:4)2
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ 16. Slope 2,y-intercept 4
5
5. Show that the points (cid:1)(cid:4)2, 9(cid:2),(cid:1)4, 6(cid:2),(cid:1)1, 0(cid:2),and (cid:1)(cid:4)5, 3(cid:2)are the 17. x-intercept 1,y-intercept (cid:4)3
vertices of a square.
18. x-intercept (cid:4)8,y-intercept 6
6. (a) Show that the points A(cid:1)(cid:4)1, 3(cid:2),B(cid:1)3, 11(cid:2),and C(cid:1)5, 15(cid:2)are
19. Through (cid:1)4, 5(cid:2),parallel to the x-axis
collinear (lie on the same line)by showing that
(cid:3) (cid:3) (cid:3) (cid:3) (cid:3) (cid:3)
AB (cid:5) BC (cid:1) AC . 20. Through (cid:1)4, 5(cid:2),parallel to the y-axis
(b) Use slopes to show that A,B,and Care collinear. 21. Through (cid:1)1, (cid:4)6(cid:2),parallel to the line x(cid:5)2y(cid:1)6
2007 7–10 Sketch the graph of the equation. 22. y-intercept 6,parallel to the line 2x(cid:5)3y(cid:5)4(cid:1)0
Brooks-Cole copyright ■79.. xxy■(cid:1)(cid:1)30■ ■ ■ ■ ■180.. (cid:3)y■y(cid:1)(cid:3)(cid:1)(cid:4)■21 ■ ■ ■ ■ 22■34.. TThh■rroouugg■hh ((cid:1)(cid:4)12, 1(cid:4)■, (cid:4)23)2,(cid:2)p■,eprperepn■ednicduicl■aurl atro tto■h eth lei nl■ein 4e x2(cid:4)x■ (cid:5)8y5■(cid:1)y(cid:5)18■(cid:1)0■
mson
Tho
6 ■ REVIEW OF ANALYTIC GEOMETRY
25–28 Find the slope and y-intercept of the line and draw 41. Show that the lines
its graph.
2x(cid:4)y(cid:1)4 and 6x(cid:4)2y(cid:1)10
25. x(cid:5)3y(cid:1)0 26. 2x(cid:4)3y(cid:5)6(cid:1)0
are not parallel and find their point of intersection.
27. 3x(cid:4)4y(cid:1)12 28. 4x(cid:5)5y(cid:1)10
42. Show that the lines
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
29–36 Sketch the region in the xy-plane. 3x(cid:4)5y(cid:5)19(cid:1)0 and 10x(cid:5)6y(cid:4)50(cid:1)0
(cid:3) (cid:3)
29. (cid:4)(cid:1)x, y(cid:2) x(cid:2)0(cid:5) 30. (cid:4)(cid:1)x, y(cid:2) x(cid:3)1 and y(cid:2)3(cid:5) are perpendicular and find their point of intersection.
31. {(cid:1)x, y(cid:2)(cid:3)(cid:3)x(cid:3)(cid:8)2} 32. {(cid:1)x, y(cid:2)(cid:3)(cid:3)x(cid:3)(cid:2)3 and (cid:3)y(cid:3)(cid:2)2} 43. Show that the midpoint of the line segment from P(cid:1)x , y (cid:2) to
1 1 1
33. (cid:4)(cid:1)x, y(cid:2)(cid:3)0(cid:8)y(cid:8)4 and x(cid:8)2(cid:5) P2(cid:1)x2, y2(cid:2)is (cid:8) (cid:9)
34. (cid:4)(cid:1)x, y(cid:2)(cid:3)y(cid:7)2x(cid:4)1(cid:5) x1(cid:5)x2, y1(cid:5)y2
(cid:3) 2 2
35. (cid:4)(cid:1)x, y(cid:2) 1(cid:5)x(cid:8)y(cid:8)1(cid:4)2x(cid:5)
36. {(cid:1)x, y(cid:2)(cid:3)(cid:4)x(cid:8)y(cid:2)1(cid:1)x(cid:5)3(cid:2)} 44. Find the midpoint of the line segment joining the points (cid:1)1, 3(cid:2)
2 and (cid:1)7, 15(cid:2).
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
37–38 Find an equation of a circle that satisfies the given 45. Find an equation of the perpendicular bisector of the line seg-
ment joining the points A(cid:1)1, 4(cid:2)and B(cid:1)7, (cid:4)2(cid:2).
conditions.
37. Center (cid:1)3, (cid:4)1(cid:2),radius 5 46. (a) Show that if the x- and y-intercepts of a line are nonzero
numbers aand b,then the equation of the line can be put in
38. Center (cid:1)(cid:4)1, 5(cid:2),passes through (cid:1)(cid:4)4, (cid:4)6(cid:2)
the form
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ x y
(cid:5) (cid:1)1
39–40 Show that the equation represents a circle and find the a b
center and radius.
This equation is called the two-intercept formof an equa-
39. x2(cid:5)y2(cid:4)4x(cid:5)10y(cid:5)13(cid:1)0 tion of a line.
40. x2(cid:5)y2(cid:5)6y(cid:5)2(cid:1)0 (b) Use part (a) to find an equation of the line whose
x-intercept is 6 and whose y-intercept is (cid:4)8.
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
2007
copyright
Brooks-Cole
mson
Tho
REVIEW OF ANALYTIC GEOMETRY ■ 7
ANSWERS
S Click here for solutions. 28. m(cid:1)(cid:4)54, b(cid:1)2
1. 5 2. 2s29 3. (cid:4)9 4. 4
2 7
7. y 8.
x=3
0 3 x
29. y 30.
9. y 10.
0 x
xy=0
0 x
31. y 32.
11. y(cid:1)6x(cid:4)15 12. y(cid:1)(cid:4)7x(cid:4)31 13. 5x(cid:5)y(cid:1)11
2 2
14. y(cid:1)x(cid:4)1 15. y(cid:1)3x(cid:4)2 16. y(cid:1)2x(cid:5)4 _2 0 2 x
5
17. y(cid:1)3x(cid:4)3 18. y(cid:1)3x(cid:5)6 19. y(cid:1)5
4
20. x(cid:1)4 21. x(cid:5)2y(cid:5)11(cid:1)0 22. y(cid:1)(cid:4)2x(cid:5)6
3
23. 5x(cid:4)2y(cid:5)1(cid:1)0 24. y(cid:1)(cid:4)2x(cid:5)31 33. y 34.
25. m(cid:1)(cid:4)1, b(cid:1)0 y y=4
3
x=2
0 x
0 x
26. m(cid:1) 32, b(cid:1)2 35. y 36.
y=1+x
(cid:1)0, 1(cid:2)
0 x
y=1-2x
27. m(cid:1)3, b(cid:1)(cid:4)3 y
4
37. (cid:1)x(cid:4)3(cid:2)2(cid:5)(cid:1)y(cid:5)1(cid:2)2(cid:1)25 38. (cid:1)x(cid:5)1(cid:2)2(cid:5)(cid:1)y(cid:4)5(cid:2)2(cid:1)130
0 x
39. (cid:1)2, (cid:4)5(cid:2), 4 40. (cid:1)0, (cid:4)3(cid:2), s7 41. (cid:1)1, (cid:4)2(cid:2) 42. (cid:1)2, 5(cid:2)
_3
44. (cid:1)4, 9(cid:2) 45. y(cid:1)x(cid:4)3 46. (b) y(cid:1)4x(cid:4)8
3
2007
copyright
Brooks-Cole
mson
Tho
8 ■ REVIEW OF ANALYTIC GEOMETRY
SOLUTIONS
1. Usethedistanceformulawith P (x ,y )=(1,1)andP (x ,y )=(4,5)toget
1 1 1 2 2 2
P P = (4 1)2+(5 1)2 =√32+42=√25=5
1 2
| | − −
(cid:115)
2. Thedistancefrom(1, 3)to(5,7)is (5 1)2+[7 ( 3)]2 =√42+102 =√116=2√29.
− − − −
(cid:115)
6 3 9
3. WithP( 3,3)andQ( 1, 6),theslopemofthelinethroughP andQism= − − = .
− − − 1 ( 3) −2
− − −
0 ( 4) 4
4. m= − − =
6 ( 1) 7
− −
5. UsingA( 2,9),B(4,6),C(1,0),andD( 5,3),wehave
− −
AB = [4 ( 2)]2+(6 9)2 = 62+( 3)2 =√45=√9√5=3√5,
| | − − − −
(cid:115) (cid:115)
BC = (1 4)2+(0 6)2 = ( 3)2+( 6)2 =√45=√9√5=3√5,
| | − − − −
(cid:115) (cid:115)
CD = ( 5 1)2+(3 0)2 = ( 6)2+32 =√45=√9√5=3√5,and
| | − − − −
(cid:115) (cid:115)
DA = [ 2 ( 5)]2+(9 3)2 =√32+62 =√45=√9√5=3√5.Soallsidesareofequallengthand
| | − − − −
(cid:116)
6 9 1 0 6 3 0 1
wehavearhombus.Moreover,mAB = 4 −( 2) =−2,mBC = 1−4 =2,mCD = 5− 1 =−2,and
− − − − −
9 3
mDA = 2 −( 5) =2,sothesidesareperpendicular.Thus,A,B,C,andDareverticesofasquare.
− − −
6. (a)UsingA( 1,3),B(3,11),andC(5,15),wehave
−
AB = [3 ( 1)]2+(11 3)2 =√42+82 =√80=4√5,
| | − − −
BC =(cid:115)(5 3)2+(15 11)2 =√22+42 =√20=2√5,and
| | − −
AC =(cid:115)[5 ( 1)]2+(15 3)2 =√62+122=√180=6√5.Thus, AC = AB + BC .
| | − − − | | | | | |
(cid:115)
11 3 8 15 3 12
(b)mAB = 3 (− 1) = 4 =2andmAC = 5 (− 1) = 6 =2.SincethesegmentsABandAChavethe
− − − −
sameslope,A,BandCmustbecollinear.
7. Thegraphoftheequationx=3isaverticalline 8.Thegraphoftheequationy= 2isahorizontal
−
withx-intercept3.Thelinedoesnothaveaslope. linewithy-intercept 2.Thelinehasslope0.
−
2007
copyright
Brooks-Cole
mson
Tho
REVIEW OF ANALYTIC GEOMETRY ■ 9
9. xy=0 x=0ory=0.Thegraph 10. y =1 y=1ory= 1
⇔ | | ⇔ −
consistsofthecoordinateaxes.
11. Bythepoint-slopeformoftheequationofaline,anequationofthelinethrough(2, 3)withslope6is
−
y ( 3)=6(x 2)ory=6x 15.
− − − −
12. y ( 5)= 7[x ( 3)]ory= 7x 31
− − −2 − − −2 − 2
6 1
13. Theslopeofthelinethrough(2,1)and(1,6)ism= − = 5,soanequationofthelineis
1 2 −
−
y 1= 5(x 2)ory= 5x+11.
− − − −
3 ( 2)
14. For( 1, 2)and(4,3),m= − − =1.Anequationofthelineisy 3=1(x 4)ory=x 1.
− − 4 ( 1) − − −
− −
15. Bytheslope-interceptformoftheequationofaline,anequationofthelineisy=3x 2.
−
16. Bytheslope-interceptformoftheequationofaline,anequationofthelineisy= 2x+4.
5
3 0
17. Sincethelinepassesthrough(1,0)and(0, 3),itsslopeism= − − =3,soanequationisy=3x 3.
− 0 1 −
−
x y
Anothermethod:FromExercise61, + =1 3x+y= 3 y=3x 3.
1 3 ⇒ − − ⇒ −
−
6 0 3
18. For( 8,0)and(0,6),m= − = .Soanequationisy= 3x+6.
− 0 ( 8) 4 4
− −
x y
Anothermethod:FromExercise61, + =1 3x+4y=24 y= 3x+6.
8 6 ⇒ − ⇒ 4
−
19. Thelineisparalleltothex-axis,soitishorizontalandmusthavetheformy=k.Sinceitgoesthroughthepoint
(x,y)=(4,5),theequationisy=5.
20. Thelineisparalleltothey-axis,soitisverticalandmusthavetheformx=k.Sinceitgoesthroughthepoint
(x,y)=(4,5),theequationisx=4.
21. Puttingthelinex+2y=6intoitsslope-interceptformgivesusy= 1x+3,soweseethatthislinehas
−2
slope 1.Thus,wewantthelineofslope 1 thatpassesthroughthepoint(1, 6):y ( 6)= 1(x 1)
−2 −2 − − − −2 − ⇔
y= 1x 11.
−2 − 2
22. 2x+3y+4=0 y= 2x 4,som= 2 andtherequiredlineisy= 2x+6.
⇔ −3 − 3 −3 −3
23. 2x+5y+8=0 y= 2x 8.Sincethislinehasslope 2,alineperpendiculartoitwouldhaveslope 5,
⇔ −5 − 5 −5 2
sotherequiredlineisy ( 2)= 5[x ( 1)] y= 5x+ 1.
− − 2 − − ⇔ 2 2
copyright 2007 24. 4rexqu−ir8edyl=ine1isy⇔− y−=23 12=x−−218.xS−inc12ethis⇔lineyha=ss−lo2pxe+12,13a.lineperpendiculartoitwouldhaveslope−2,sothe
Brooks-Cole (cid:3) (cid:4) (cid:3) (cid:4)
mson
Tho
10 ■ REVIEW OF ANALYTIC GEOMETRY
25. x+3y=0 y= 1x, 26.2x 3y+6=0 27.3x 4y=12
⇔ −3 − ⇔ − ⇔
sotheslopeis 1 andthe y= 2x+2,sotheslopeis 2 y= 3x 3,sotheslopeis 3
−3 3 3 4 − 4
y-interceptis0. andthey-interceptis2. andthey-interceptis 3.
−
28. 4x+5y=10 29. (x,y) x<0 30. (x,y) x 1andy<3
⇔ { | } { | ≥ }
y= 4x+2,sotheslopeis
−5
4 andthey-interceptis2.
−5
31. (x,y) x 2 = 32. (x,y) x <3and y <2 33. (x,y) 0 y 4,x 2
| |≤ | | | | { | ≤ ≤ ≤ }
(cid:113) (cid:15) (cid:114) (cid:113) (cid:15) (cid:114)
(x,y) (cid:15) 2 x 2 (cid:15)
{ |(cid:15)− ≤ ≤ } (cid:15)
34. (x,y) y>2x 1 35. (x,y) 1+x y 1 2x 36. (x,y) x y< 1(x+3)
{ | − } { | ≤ ≤ − } |− ≤ 2
(cid:11) (cid:12)
37. Anequationofthecirclewithcenter(3, 1)andradius5is(x 3)2+(y+1)2 =52 =25.
− −
38. Theequationhastheform(x+1)2+(y 5)2 =r2. Since( 4, 6)liesonthecircle,wehave
− − −
r2=( 4+1)2+( 6 5)2 =130.Soanequationis(x+1)2+(y 5)2 =130.
− − − −
39. x2+y2 4x+10y+13 =0 x2 4x+y2+10y = 13
− ⇔ − − ⇔
2007 x2−4x+4 + y2+10y+25 =−13+4+25=16 ⇔ (x−2)2+(y+5)2 =42.Thus,wehavea
copyright (cid:3)circlewithcen(cid:4)ter((cid:3)2,−5)andradiu(cid:4)s4.
Brooks-Cole
mson
Tho