Power Amplifiers PDF
Preview Power Amplifiers
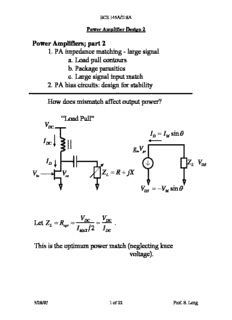
ECE 145A/218A Power Amplifier Design 2 Power Amplifiers; part 2 1. PA impedance matching - large signal a. Load pull contours b. Package parasitics c. Large signal input match 2. PA bias circuits: design for stability How does mismatch affect output power? “Load Pull” V DC I = I sinθ D M I DC g V m gs I Z V D L DS V V Z = R + jX in os L V = −V sinθ DS M V V Let Z = R = DC = DC . L opt I 2 I MAX DC This is the optimum power match (neglecting knee voltage). 5/28/07 1 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 V I P = DC DC opt 2 2 V 1 = DC = I2 R DC opt 2R 2 R opt opt V DC 0 I max I D Full voltage and I DC current swing. (neglecting V ) knee 0 5/28/07 2 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 Ref. S. Cripps, RF Power Amplifiers for Wireless Communications, Artech House, 1999. 5/28/07 3 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 To determine the influence of a mismatched load on the power amplifier output power and also efficiency, we must trace out a contour on the Smith Chart that will give a power of P / p. Here, p is the power reduction factor. opt There are two solutions. Resistive Terminations ⎧ V 1) pR ⎪⎨Im = pRDoCpt P = 1 VD2C = Popt OPT o 2 pR p ⎪ opt V =V ⎩ m DC 2) Ropt ⎧⎪Im = Imax / 2 =IDC 1 ID2CRopt Popt p ⎨ P0 = = 2 p p ⎪V = I R / p ⎩ m DC opt R = P / p HI opt R opt R R = opt LO P 5/28/07 4 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 R Series reactance; When R = opt =R , add jX. LO p jX R / p = R V = I R + jX opt LO M DC LO in this limit when R = R , we have power limited by I . LO MAX Voltage V < V . So, series reactance will increase the m DC voltage swing but not affect current. This is valid up to ±X , where R + jX = R m LO m opt Shunt susceptance; When R = pR =R , add jB opt HI jB 1 G = pR opt at this limit, power is limited by the voltage swing, V = V . I < I . m DC D MAX 5/28/07 5 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 Shunt susceptance can be added. It will cause current to increase until 1 G + jB = m R opt These are called Load Pull Contours, and they follow constant r or g circles on Smith Chart. It can be shown that the intersection of these circles represents X or B . m m Po = P /p Boundary for opt Boundary for P = P / p 0 opt 5/28/07 6 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 Ref. S. Cripps, RF Power Amplifiers for Wireless Communications, Artech House, 1999. The load pull contour takes the place of gain circles for power amplifier designs. 5/28/07 7 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 At higher frequencies, device capacitances and package capacitance and inductance can be significant. A L pkg R C C L out 1 B Utilize C as part of matching network- OUT • a pi-section can accomplish this if C and L is not extremely large. OUT pkg • Smith chart or design equations can be used to design network. Q ≤ 5 is reasonable for narrowband design. • Note that we must provide the load line match at plane A, not plane B. 5/28/07 8 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 What does the package do to Z ? L A B large small x , b L c B A L pkg R opt C out We require that ZA = Ropt, so there is a problem – the output capacitance and the package will transform Ropt into something else. So, Ropt must be compensated to account for the package. 5/28/07 9 of 22 Prof. S. Long ECE 145A/218A Power Amplifier Design 2 Input Matching For PAs, we often have large voltage or current variations on input. This can lead to large input impedance variation with drive power, P . IN So, what procedure can be used to design input network? For Class A, we never cutoff or swing into knee region of device I-V. - 1st approximation: use small signal S parameter calculation to find Γ at quiescent bias. IN - Conjugately match the input. - If gain is adequate, stop. Otherwise, you may need to optimize Γ experimentally in simulation. (source S pull) 5/28/07 10 of 22 Prof. S. Long
Description: