Notes 9c: Two-way ANOVA with Interactions 1. What is

24 Pages·2010·0.23 MB·English

by  Bryan W. Griffin

1
Notes 9c: Two-way ANOVA with Interactions

1. What is an Interaction?
An interaction occurs when an independent variable's statistical effects (or differences) upon the dependent
variable varies or differ across levels of a second independent variable.

(a) Examples of Interactions
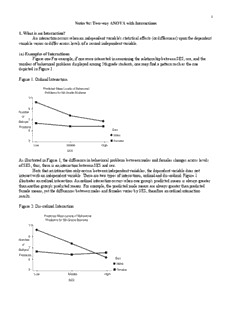
Figure one For example, if one were interested in examining the relationship between SES, sex, and the
number of behavioral problems displayed among 5th grade students, one may find a pattern such as the one
depicted in Figure 1.

Figure 1: Ordinal Interaction

Predicted Mean Levels of Behavioral
Problems for 5th Grade Students
11
9
Number
of
7
Behave
Problems
5 Sex
Males
3 Females
Low Middle High
SES

As illustrated in Figure 1, the difference in behavioral problems between males and females changes across levels
of SES; thus, there is an interaction between SES and sex.
Note that an interaction only occurs between independent variables; the dependent variable does not
interact with an independent variable. There are two types of interactions, ordinal and dis-ordinal. Figure 1
illustrates an ordinal interaction. An ordinal interaction occurs when one group's predicted means is always greater
than another group's predicted means. For example, the predicted male means are always greater than predicted
female means, yet the differences between males and females varies by SES, therefore an ordinal interaction
results.

Figure 2: Dis-ordinal Interaction

Predicted Mean Levels of Behavioral
Problems for 5th Grade Students
11
9
Number
of
7
Behave
Problems
5 Sex
Males
3 Females
Low Middle High
SES
2
When two or more group means switch or cross, a disordinal interaction occurs. Figure 2 illustrates a
disordinal interaction. Note that predicted male means are higher for low and middle levels of SES, but the
predicted female mean for high levels of SES is greater than the predicted male mean.

(b) Examples Without Interactions
Figures 3a and 3b, which contain no interactions, are included as a reference. Note that the differences
between males and females is constant in both a and b, i.e., the sex difference does not vary by SES level.

Figure 3

(a)
Predicted Mean Levels of Behavioral
Problems for 5th Grade Students
11
9
Number
of
7
Behave
Problems
5 Sex
Males
3 Females
Low Middle High
SES
(b)
Predicted Mean Levels of Behavioral
Problems for 5th Grade Students
11
9
Number
of
7
Behave
Problems
5 Sex
Males
3 Females
Low Middle High
SES
3
2. Two-way ANOVA with Interaction
Sometimes interactions can mask main effects of factors (IVs). Below is a very simple example illustrating
the masked effect using achievement as the DV and instruction type and student sex as the IV or factors.

Table 1
Example Date for Two-way ANOVA with Interaction
Achievement Instruction Type Sex
74 Co-operative m
76 Co-operative m
84 Co-operative f
86 Co-operative f
78 Lecture m
82 Lecture m
79 Lecture f
81 Lecture f
86 Self-paced m
84 Self-paced m
76 Self-paced f
74 Self-paced f

(a) Data Plotted – What do the plots show?

These data are plotted here:

https://spreadsheets.google.com/ccc?key=0AoKw33oyzB1NdDVTcnk5ZVhOaWp0bGpERHNBQ3hhdEE&hl=en
&authkey=COzWuIYD

(b) Table of Means and Marginal Means – What does this show?

Table 2
Means and Marginal Means for Sample
Coop Lecture Self Marginal Means for Sex
Female 85.00 80.00 75.00 80.00
Male 75.00 80.00 85.00 80.00

Marginal Means for Instruction 80.00 80.00 80.00

With these marginal means, would we reject the null hypothesis for sex or for instruction?

H (sex): μ = μ
0 males. females.

H (instruction): μ = μ = μ
0 .coop .lecture .self

As before the dots indicate average across levels of the other factors, that is, hypotheses tests are based upon
marginal means.
4
(c) ANOVA Summary Without Interaction – What do these results indicate?

Tests of Between-Subjects Effects
Type III Sum
Source of Squares df Mean Square F Sig.
Corrected Model .000(a) 3 .000 .000 1.000
Intercept 76800.000 1 76800.000 2818.349 .000
instruction .000 2 .000 .000 1.000
sex .000 1 .000 .000 1.000
Error 218.000 8 27.250
Total 77018.000 12
Corrected Total 218.000 11
a R Squared = .000 (Adjusted R Squared = -.375)

1. instruction
95% Confidence Interval
Lower Upper
instruction Mean Std. Error Bound Bound
Co-operative 80.000 2.610 73.981 86.019
Lecture 80.000 2.610 73.981 86.019
Self-paced 80.000 2.610 73.981 86.019

2. sex
95% Confidence Interval
Lower Upper
sex Mean Std. Error Bound Bound
f 80.000 2.131 75.086 84.914
m 80.000 2.131 75.086 84.914

In summary, what is the possible result of the ANOVA hypothesis tests if only marginal means are examined
without regard to interactions?

(d) ANOVA Summary With Interaction – What do these results indicate?

Tests of Between-Subjects Effects
Type III
Sum of
Source Squares df Mean Square F Sig.
Corrected Model 200.000(a) 5 40.000 13.333 .003
Intercept 76800.000 1 76800.000 25600.000 .000
instruction .000 2 .000 .000 1.000
sex .000 1 .000 .000 1.000
instruction * sex 200.000 2 100.000 33.333 .001
Error 18.000 6 3.000
Total 77018.000 12
Corrected Total 218.000 11
a R Squared = .917 (Adjusted R Squared = .849)
5
3. Two-way ANOVA Model with Interaction
Two-way ANOVA with interaction is simply an ANOVA with two qualitative independent variables and
the interaction between them.

(a) Regression Model Without Interaction
The multiple regression model for a two-way ANOVA without interaction looks like this:

Y’ = b + b coop + b self + b female
0 1 2 3

where “coop,” “self,” and “female” are dummy variables and the omitted categories (reference group) are males in
the lecture treatment.

(b) Creating Interactions in Regression
To form interactions one multiples the IVs and includes those product terms in the regression model. For
example, consider two predictors X and Z. As a general example, the interaction between X and Z is found by
including in the regression model the following product:

Interaction (XZ) = X * Z.

When one or more of the independent variables is categorical, each dummy representing the variable must be
multiplied. For the current example, there will be two multiplicative terms to include in the regression model:

coop×female = coop × female

self×female = self × female

(c) Regression Model With Interaction
Entering these terms into the sample regression model results in the following equation:

Y’ = b + b coop + b self + b female + b coop×female + b self×female
0 1 2 3 4 5

(d) ANOVA with interaction
In most software one does not have to produce the underlying linear model as is done in regression above.
Instead, one simply specifies the model and the software creates the linear equation. For ANOVA the model would
appear as follows:

Y’ = Intercept + Instruction + Sex + I×S

where “I” represents instruction and “S” represents sex.

4. Hypotheses
The hypotheses remain essentially unchanged from previously with ANOVA except comparisons now
must be specified as “main effect” or “simple main effect.”

(a) Main Effect Tests
This is the same hypothesis test of group comparisons that have been discussed previously in ANOVA, i.e.:

Instruction
H : μ .= μ .= μ . (taking mean across both males and females for each category of instruction)
0 1 2 3
H : not all of the instructional treatments means are equal
a

Sex
H : μ .= μ . (taking mean across all levels of instruction)
0 1 2
H : μ .≠ μ ..
a 1 2
6

(b) Interaction Test
Interaction between the two independent variables

H : αβ = 0
0
H : αβ ≠ 0
a

where αβ represent the interaction product of multiplying two factors such as sex and instruction.

(c) Simple Main Effects
If the interaction is statistically significant, then focus will be upon not Main Effects tests, but upon Simple
Main Effects tests. A simple main effect just means that one makes comparisons, or hypotheses tests, for one
variable by each level (or category) of the second variable if both variables are categorical.

Simple main effects hypothesis testing can also occur where the IVs are quantitative. The situation where one IV is
quantitative and the second is qualitative will be discuss in ANCOVA. In the situation where both IVs are
quantitative will be covered in regression.

As the example data discussed above “2. Two-way ANOVA with Interaction” shows, if one examines the
marginal means the interpretation of results can be misleading if an interaction is present. This may not be true in
some types of interactions (such as a weak ordinal interaction), but one should examine the simple main effects
whenever an interaction is statistically significant.

Table 3
Means and Marginal Means for Sample
Coop Lecture Self Marginal Means for Sex
Female 85.00 80.00 75.00 80.00
Male 75.00 80.00 85.00 80.00

Marginal Means for Instruction 80.00 80.00 80.00

(c.1) Sex Simple Main Effects
Requires three separate t-tests, one for each instructional condition:

Cooperative Learning Comparison
Male vs. Female in Cooperative Learning condition:
H0: μ1Coop = μ2coop (85−75)
H : μ ≠ μ t test =
1 1Coop 2coop se
difference

Lecture Comparison
Male vs. Female in Lecture condition:
H0: μ1Lecture = μ2Lecture (80−80)
H : μ ≠ μ t test =
1 1Lecture 2Lecture se
difference

Self-paced Comparison
Male vs. Female in Self-paced condition:
H0: μ1Self = μ2Self (75−85)
H : μ ≠ μ t test =
1 1Self 2Self se
difference
7
(c.2) Instruction Simple Main Effects
Requires multiple comparisons separately for each sex:

Comparisons for Females
Comparison Adjusted Mean Standard Error of 95% CI
Difference Mean Difference
Coop vs. Self 10
Coop vs. Lecture 5
Self vs. Lecture -5

Comparisons for Males
Comparison Adjusted Mean Standard Error of 95% CI
Difference Mean Difference
Coop vs. Self -10
Coop vs. Lecture -5
Self vs. Lecture 5

5. ANOVA Computation
As before, ANOVA computation is based upon the information found in the summary table below.

Table 4
Two-way ANOVA Summary Table
Source SS df MS F
Factor A SS df = j - 1 SS /df MS /MS
A A A A A w
Factor B SS df = k - 1 SS /df MS /MS
B B B B B w
Interaction A×B SS df = (j – 1)(k-1) SS /df MS /MS
AB AB AB AB AB w
Within Error SS df = jk(n-1) SS /df
W w w w
total SS df = n - 1
T t

6. SPSS Results for Sample Data
SPSS results of the two-way ANOVA are provided below. The GENERAL LINEAR MODEL-
>UNIVARIATE command was used, and a model with interaction was specified (this is done automatically in
SPSS). This will be illustrated during the chat.

To obtain simple main effect comparisons will require use of SPSS syntax commands since the Window’s pull-
down menus don’t contain this option (at least with my version of SPSS). SPSS Syntax (commands) and the part
added in bold and underlined:

UNIANOVA
achievement BY instruction sex
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/EMMEANS = TABLES(instruction) COMPARE ADJ(BONFERRONI)
/EMMEANS = TABLES(sex) COMPARE ADJ(BONFERRONI)
/EMMEANS = TABLES(instruction*sex) Compare (instruction) ADJ(BONFERRONI)
/EMMEANS = TABLES(instruction*sex) Compare (sex)
/PRINT = DESCRIPTIVE
/CRITERIA = ALPHA(.05)
/DESIGN = instruction sex instruction*sex .
8
To keep output simple, better not to seek output showing comparisons for main effects, so the lines in gray and with
strikeout can be deleted:

UNIANOVA
achievement BY instruction sex
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/EMMEANS = TABLES(instruction) COMPARE ADJ(BONFERRONI)
/EMMEANS = TABLES(sex) COMPARE ADJ(BONFERRONI)
/EMMEANS = TABLES(instruction*sex) Compare (instruction) ADJ(BONFERRONI)
/EMMEANS = TABLES(instruction*sex) Compare (sex)
/PRINT = DESCRIPTIVE
/CRITERIA = ALPHA(.05)
/DESIGN = instruction sex instruction*sex .

Results are presented below.

Descriptive Statistics
instruction sex Mean Std. Deviation N
Co- f 85.0000 1.41421 2
operative
m 75.0000 1.41421 2
Total 80.0000 5.88784 4
Lecture f 80.0000 1.41421 2
m 80.0000 2.82843 2
Total 80.0000 1.82574 4
Self-paced f 75.0000 1.41421 2
m 85.0000 1.41421 2
Total 80.0000 5.88784 4
Total f 80.0000 4.60435 6
m 80.0000 4.73286 6
Total 80.0000 4.45176 12

Tests of Between-Subjects Effects
Type III Sum
Source of Squares df Mean Square F Sig.
Corrected Model 200.000(a) 5 40.000 13.333 .003
Intercept 76800.000 1 76800.000 25600.000 .000
instruction .000 2 .000 .000 1.000
sex .000 1 .000 .000 1.000
instruction * sex 200.000 2 100.000 33.333 .001
Error 18.000 6 3.000
Total 77018.000 12
Corrected Total 218.000 11
a R Squared = .917 (Adjusted R Squared = .849)
9
Pairwise Comparisons
Dependent Variable: achievement
Mean Difference Std. 95% Confidence Interval for
sex (I) instruction (J) instruction (I-J) Error Sig.(a) Difference(a)
Lower Bound Upper Bound
f Co-operative Lecture 5.000 1.732 .083 -.694 10.694
Self-paced 10.000(*) 1.732 .004 4.306 15.694
Lecture Co-operative -5.000 1.732 .083 -10.694 .694
Self-paced 5.000 1.732 .083 -.694 10.694
Self-paced Co-operative -10.000(*) 1.732 .004 -15.694 -4.306
Lecture -5.000 1.732 .083 -10.694 .694
m Co-operative Lecture -5.000 1.732 .083 -10.694 .694
Self-paced -10.000(*) 1.732 .004 -15.694 -4.306
Lecture Co-operative 5.000 1.732 .083 -.694 10.694
Self-paced -5.000 1.732 .083 -10.694 .694
Self-paced Co-operative 10.000(*) 1.732 .004 4.306 15.694
Lecture 5.000 1.732 .083 -.694 10.694
Based on estimated marginal means
* The mean difference is significant at the .05 level.
a Adjustment for multiple comparisons: Bonferroni.

Pairwise Comparisons
Dependent Variable: achievement
Mean Std. 95% Confidence Interval for
instruction (I) sex (J) sex Difference (I-J) Error Sig.(a) Difference(a)
Lower Bound Upper Bound
Co-operative f m 10.000(*) 1.732 .001 5.762 14.238
m f -10.000(*) 1.732 .001 -14.238 -5.762
Lecture f m .000 1.732 1.000 -4.238 4.238
m f .000 1.732 1.000 -4.238 4.238
Self-paced f m -10.000(*) 1.732 .001 -14.238 -5.762
m f 10.000(*) 1.732 .001 5.762 14.238
Based on estimated marginal means
* The mean difference is significant at the .05 level.
a Adjustment for multiple comparisons: Least Significant Difference (equivalent to no adjustments).

The above two tables show simple main effects – comparisons of categories in one IV per levels of categories of a
second IV. For example, for each level of sex, the possible pairwise comparisons of instruction are present per sex:

For males the follow pairwise comparisons are provided:

Co-operative Lecture
Self-paced
Lecture Co-operative
Self-paced
Self-paced Co-operative
Lecture

And for females, the same pairwise comparisons are provided. If main effects for instruction were examined, the
pairwise comparisons for instruction would be taken across both sexes simultaneously as marginal means, not
separately as means per sex.
10
5. APA Styled Presentation

Table 5
ANOVA Results and Descriptive Statistics for Achievement by Student Sex and
Instruction Type
Variable Mean SD n
Female
Coop 85.00 1.41 2
Self 75.00 1.41 2
Lecture 80.00 1.41 2
Male
Coop 75.00 1.41 2
Self 85.00 1.41 2
Lecture 80.00 1.41 2
Source SS df MS F
Instruction (I) 0.00 2 0.00 0.00
Sex (S) 0.00 1 0.00 0.00
I×S 200.00 2 100.00 33.33*
Error 18.00 6 3.00
Note: R2 = .92, adj. R2 = .85. Coop = co-operative learning, Self = self-paced,
and Lecture = lecture instruction.
* p < .05

Table 6
Comparisons of Mean Differences in Achievement by Instruction and Student Sex
Comparison by Estimated Mean Standard Error of Bonferroni
Student Sex Difference Difference Adjusted 95% CI
Females
Coop vs. Lecture 5.00 1.73 -0.69, 10.69
Coop vs. Self 10.00* 1.73 4.31, 15.69
Lecture vs. Self 5.00 1.73 -0.69, 10.69
Males
Coop vs. Lecture -5.00 1.73 -10.69, 0.69
Coop vs. Self -10.00* 1.73 -15.69, -4.31
Lecture vs. Self -5.00 1.73 -10.69, 0.69
Note: Coop = co-operative learning, Self = self-paced, And Lecture = lecture instruction.
* p < .05, where p-values are adjusted using the Bonferroni method.

Table 7
Comparisons of Mean Differences in Achievement by Student Sex and Instruction
Comparison by Estimated Mean Standard Error of
95% CI
Instruction Difference Difference
Cooperative Learning
Female vs. Male 10.00* 1.73 5.76, 14.24
Lecture
Female vs. Male 0.00 1.73 -4.24, 4.24
Self-paced
Female vs. Male -10.00* 1.73 -14.24, -5.76
Note: Coop = co-operative learning, Self = self-paced, And Lecture = lecture instruction.
* p < .05.