NASA Technical Reports Server (NTRS) 20100024244: A State-Space Approach to Optimal Level-Crossing Prediction for Linear Gaussian Processes

0.43 MB·English

by  NASA Technical Reports Server (NTRS)

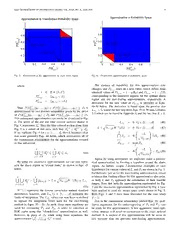
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 1
A State-Space Approach to Optimal Level-Crossing
Prediction for Linear Gaussian Processes
Rodney A Martin, Ph.D. Member, IEEE
Abstract—In many complex engineered systems, the ability predictive capability, but have no provision for minimizing
to give an alarm prior to impending critical events is of great false alarms for the prediction of level-crossing events.
importance. These critical events may have varying degrees of
There are several examples of level-crossing events to be
severity,andinfacttheymayoccurduringnormalsystemopera-
studied, varying from a simple one-sided case to a more com-
tion.Inthisarticle,weinvestigateapproximationstotheoretically
optimalmethodsofdesigningalarmsystemsforthepredictionof plicated two-sided case. The former one-sided case involves
level-crossings by a zero-mean stationary linear dynamic system exceedancesand/orupcrossingsofasinglelevelspanningtwo
driven by Gaussian noise. An optimal alarm system is designed adjacent time points for a discrete-time process. This is the
to elicit the fewest false alarms for a fixed detection probability.
case that has traditionally been studied in previous work and
ThisworkintroducestheuseofKalmanfilteringintandemwith
invokes ARMA(X) prediction methods [1], [2], [4], [5], [6],
the optimal level-crossing problem. It is shown that there is a
negligiblelossinoverallaccuracywhenusingapproximationsto [7]. The latter two-sided case involves a level crossing event
the theoretically optimal predictor, at the advantage of greatly that may span many time points and exceed upper and lower
reduced computational complexity. levels symmetric about the mean of the process many times
Index Terms—Optimal alarm theory, Level-crossing theory, during this timeframe.
Kalman prediction Avariantofthelattermorecomplicatedtwo-sidedcasehas
been investigated by Kerr [8] and uses a Kalman filter-based
approach. The two-sided case is more practically relevant
I. INTRODUCTION
when monitoring residuals that may be derived from the
THIS article introduces a novel approach of combining output of other machine learning algorithms or transformed
the practical appeal of Kalman filtering with the design parameters that relate to system performance. We investigate
of an optimal alarm system for the prediction of level- the two-sided case here, and also use a Kalman filter-based
crossing events. A comprehensive demonstration of practical approach in an optimal manner relevant for the prediction of
application for the design of optimal alarm systems has been level-crossings.
coveredintheliterature[1],[2],[3].However,thebackground The prediction of such a level-crossing event is also very
theory for optimal alarm systems has seen modest coverage similar to what has been established as the state of the art for
by other authors as well [4], [5], [6], [7]. The latter is by no newly minted spacecraft engines, as studied in [9], however
means a comprehensive list, but illustrates a cross-section of no guarantees of optimality exist. This provide us additional
the primary authors responsible for introducing optimal alarm practicalmotivationforinvestigatingalevelcrossingeventthat
systems in a classical and practical sense. spans many time points, moving beyond what has previously
It was shown by Svensson [1], [2] that an optimal alarm been studied in this vein. In general, the design of optimal
system can be constructed by finding relevant alarm system alarm systems demonstrates practical potential to enhance re-
metrics(asareusedinROCcurveanalysis)asafunctionofa liability and support health management for space propulsion,
design parameter by way of an optimal alarm condition. The civil aerospace applications, and other related fields. Due to
optimal alarm condition is fundamentally an alarm region or the great costs, not to mention potential dangers associated
decision boundary based upon a likelihood ratio criterion via with a false alarm due to evasive or extreme action taken
the Neyman-Pearson lemma, as shown in [5], [6]. This allows as a result of false indications, there are great opportunities
ustodesignanoptimalalarmsystemthatwillelicitthefewest for cost savings/cost avoidance, and enhancement of overall
possiblefalsealarmsforafixeddetectionprobability.Thisbe- safety. Nonetheless, our intent is to demonstrate the utility
comes important when considering the numerous applications of optimal level-crossing prediction from a more theoretical
that might benefit from an intelligent tradeoff between false perspective.
alarms and missed detections. There is an extensive history of invoking Kalman-filter-
Due to the fact that optimal alarm regions cannot be basedapproacheswithinthefailuredetectionliterature.Afew
expressed in closed form, one of the aims of this study is of the most groundbreaking articles that discuss the use of
to investigate approximations for the design of an optimal Kalmanfiltermethodsforfailuredetectionhavebeenauthored
alarm system. The resulting metrics can easily be compared by Kerr [8], and Willsky and Jones [10]. Both of these
to competing methods that may also provide some level of articles have a long history of related methods descending
from them, i.e., [11] which alludes to the use of the Neyman-
Manuscript received xxx xx, 2007; revised xxx xx, 2009. This work was
Pearson lemma. More recently, the use of the Kalman filter
supportedbyxxxx.
RodneyA.MartiniswiththeNASAAmesResearchCenter hasbeenusedtoaddressthelevel-crossingpredictionproblem
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 2
in application to condition monitoring [12], however without selectionmaybeperformedwiththeaidofROCanalysis.The
any theoretical guarantees of optimality. A competitor to the main utility of using two distinct levels, however, is to enable
optimal alarm system is described in [13], and uses adap- thedecouplingofalarmdesignfromconstructionofthecritical
tive optimal on-line techniques in a Bayesian formulation, event itself. Two levels are also often used in practice for the
providing more modeling flexibility. However, there are still design of fault detection algorithms that involve limit-based
considerable computational issues with such an approach, and abort decisions. A “yellow-line” limit check is often used as
a well-defined cost function is still required, even when the a precursor caution and warning threshold to the “redline”
posterior probability is adaptively updated. abort threshold. The former can be used as an alarm system
One recent criticism of [10] addresses the claim of its design parameter, where the latter may serve as a hard limit
optimality by Kerr [14]. This method, presented by Willsky determined apriori via extensive experimental validation.
and Jones, is characterized by a formulation of the failure To recap, the redline and predictive techniques both use
detectionprobleminvolvingtheGLR(GeneralizedLikelihood fixed thresholds, L , and the optimal level-crossing predictor
A
Ratio) test. The method derived by Kerr shows how to derive uses an optimal alarm condition (or approximations of it).
a failure detection algorithm whose design is performed by Allthreetechniquesareleveragedtopredictanotherdistinctly
computing false alarm and correct detection probabilities over morecriticallevel-crossingevent(baseduponthecriticallevel,
a time interval. Neither method is optimal in the sense used L), and all are preferable to the use of a single level for a
to predict level-crossings, as introduced by DeMare´ [5] and numberofreasons.Forone,ROCcurvestatistics(thetrueand
Svensson et al. [2]. Other standard methods based upon the false positive rates) can be expressed directly as a function of
GLRtest,andSPRT(SequentialProbabilityRatioTest)invoke themodelparameterswhenusingthesetechniques.Therefore,
hypothesis tests that are geared more for detection of the design of the alarm system can proceed without the need to
change of model parameters, as opposed to level-crossings. observe actual examples of failures, and there is no need to
As was previously mentioned in this section, we aim to estimate the alarm system metrics empirically. This obviates
more precisely close the gap between the use of Kalman the need to rely upon having actual available examples of
filtering and optimal alarm systems in this article. Although failures for alarm system design to generate the ROC curve.
this article is motivated by fault detection and prediction, It is not possible to construct an ROC curve as a function
and it is recognized that the literature in this area is quite of model parameters when using a single level. In this case
expansive, our investigation aims to shed light on a segment the ROC curve statistics can only be estimated empirically
of the literature that has been largely overlooked. with observational and truth data. Truth data in this case
can either be represented by model generated level-crossing
events, or failures generated from a complex system. The
II. PERFORMANCEANALYSIS
construction of an ROC curve in this manner can be used for
As mentioned previously, relevant alarm system metrics anyalarmsystemtechnique.However,intheabsenceofactual
suchasonesusedinROCcurveanalysiscanbeexpressedasa observations of failures, the “Monte-Carlo” style method of
functionofadesignparameterviaanoptimalalarmcondition. generating truth data can be computationally intensive, and
These same metrics will act as the basis for comparison is still based purely upon simulated model-generated level-
to competing methods that are functions of different design crossings. As such, it is imperative that the gap between
parameters.Thesecompetingmethodsmayprovidesomelevel model-generated failures and actual observations of failures
of predictive capability, but have no provision for minimizing be made as small as possible. The level-crossing event must
false alarms. The two primary methods to provide a baseline sufficiently characterize an actual physical failure to realize
for comparison are to compare the process value with a the advantage of expressing the ROC curve of as a function
fixed threshold, or the “redline” method, and to compare of the model parameters, and thus to design an alarm system
future predicted process value with a fixed threshold, or the without the need to observe actual examples of failures.
“predictive” method. The redline, predictive, and optimal techniques are prefer-
However, in both cases it is important to make the distinc- abletotheuseofasinglelevelforanotherreason.Theformer
tion between the critical level, L, associated with the level three techniques generate ROC curve statistics that are based
crossing event to be predicted and the fixed threshold referred upon the use of distinct design spaces for construction of a
to above, denoted as L . The critical level represents the critical event and their respective alarm systems, providing a
A
thresholdabovewhichdamageorsomesignificantdecreasein measure of functional distinction. The critical event can be
quality of a behavior or process may potentially occur. There constructed such that multiple level-crossings span multiple
are some cases in which this critical level, L, is not known, time steps into the future, implicitly enabling a predictive
havenotbeendesignedapriori,orwhenknowncriticallevels assessment capability for alarm system design. Using a single
yield alarm systems that are practically infeasible. As such, level-based alarm system merges the functionality of limit
sometimes it is beneficial to use values that are based upon checking and the use of an alarm design parameter. As such
statistical outlier detection and hypothesis testing via the p- it is not possible to decouple independent alarm design from
value. thecriticalevent,andthusthismethodprovidesnomeasureof
The fixed threshold, L , essentially acts as a design pa- functionaldistinction.Itisalsotheonemostcommonlyfound
A
rameter with which to tune the alarm system sensitivity. Its intheliterature,i.e.,[15],[8],[10].Arguably,thecriticalevent
valueisthelevelatwhichanalarmwouldbetriggered,whose shouldbeconstructedtoemulatethephysicsofthefailure,and
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 3
the alarm system should independently be designed to predict Mathematical Nomenclature
Representation
it. The distinction between these two paradigms is one of the
mostdiscernabledifferencesinthetheoreticaltechniquesused µ• E[•](Expectation)
ˆ•k+j|k E[•|y0,...,yk](ConditionalExpectation)
here and in other literature, [1], [2], [3], [4], [5], [6]. ˜•k Orthonormalrotationof•k invectorspace
Result of vector space orthonormal rotation in
•∗
probabilityoreventspace
III. METHODOLOGY
Pk+i,k+j Stateautocovariancematrix
A level-crossing event is defined with a critical level, L, PL SolutiontoDiscreteAlgebraicLyapunovEquation
ss
that is assumed to have a fixed, static value. The level is PR SolutiontoDiscreteAlgebraicRiccatiEquation(A
ss prioristeady-stateerrorcovariancematrix)
exceeded by some critical parameter than can be represented PˆR (Aposterioristeady-stateerrorcovariancematrix)
ss
by a dynamic process, and is often modeled as a zero-mean Fk+1|k KalmanGain
stationary linear dynamic system driven by Gaussian noise. Fss Steady-StateKalmanGain
Most of the theory that follows is based upon this standard V Conditional prediction variance for future output
k+j|k value
representationoftheoptimallevel-crossingproblem.Assuch,
Ck Level-crossingevent
our underlying assumption is that we can fit measured or Sk+j Level-crossingsubevent(disjoint)
transformed data to a model represented by a linear dynamic Ek+j Level-crossingsubevent(non-disjoint)
I Universeofallevents
system driven by Gaussian noise. The state-space formulation
is shown in Eqns. 1-3, demonstrating propagation of both Ak Optimalalarmevent(sublevelset)
Region in vector space spanned by level-crossing
the state, xk ∈ Rn which is corrupted by process noise ΩC event
wwikth∈thRent,imaned-inthvaerisatanttescyostveamriamncaetrimxaAtri.xT,hPeko,uwtphuict,hyevo∈lvRe LA Loledveflorse“trefodrlinoep”timanadla“lparremdiecvtievnet”omredtehsoidgsnthresh-
k Sublevel set for subevent (used in root-finding
is univariate, and is corrupted by measurement noise vk ∈R. ΩAj approximationtooptimalalarmevent)
Aj Sublevel set for subevent (used in closed-form
k approximationtooptimalalarmevent)
xk+1 = Axk+wk (1) Ai,j Sublevel set for decomposed subevent (used in
k closed-formapproximationtooptimalalarmevent)
P yk == ACxPkA+Tvk+Q ((23)) LAj Ltioevnetloseotpftiomraslubaelavremnte(vuesnetd)in(either)approxima-
k+1 k L Criticallevel
d Predictionhorizon
where
Pb BorderProbability
wk ∼ N(0,Q), Q(cid:23)0 PPbdcrit CDreitteiccatiloBnoPrrdoebraPbriloibtyability(DomainBoundary)
vk ∼ N(0,R), R>0 Pfa FalseAlarmProbability
x ∼ N(µ ,P ) TABLEI
0 x 0
SUMMARYOFMATHEMATICALNOTATION
Asummaryofthenotationtobeusedhenceforthisprovided
in Table I. As mentioned previously, there is great flexibility
in constructing a mathematical representation for the level- overlapping subevents, E(cid:48) . However, due to DeMorgan’s
k+j
crossingevent,Ck.Ostensibly,thetargetapplicationwilldrive theorem,thelattercanbeexpressedinamorecompactfashion
the definition of this event. As such, in this paper the event viaasingletermwhencomputingtheprobabilityoftheoverall
of interest is shown in Eqn. 4, cf. Kerr [8] in consideration event.Thisobviatestheneedforuseoftheinclusion/exclusion
of the motivating factors described in the introduction. This rule for the realization of all relevant terms in a probability
level-crossingeventrepresentsatleastoneexceedanceoutside computation based upon the union of overlapping subevents,
of the threshold envelope specified by [−L,L] of the process E(cid:48) , where the number of terms would be exponential in d.
k+j
yk within the specified look-ahead prediction window, d. It also obviates the need for computing the probability based
upontheformerunionofdisjointsubevents,S ,wherethere
k+j
d d d isnoneedforuseoftheinclusion/exclusionrule.However,the
C =(cid:52) (cid:91) S = (cid:91) E(cid:48) =I\ (cid:92) E (4) number of terms would still be linear in d, as the probability
k k+j k+j k+j
j=1 j=1 j=1 computation of the union of disjoint subevents is represented
by the sum of terms involving S . Thus Eqn. 5 represents
where k+j
the unconditional probability of the level-crossing event in its
most compact representational form.
(cid:52)
E = {|y |<L}, ∀j ≥1
k+j k+j
(cid:26) E(cid:48) j =1
S =(cid:52) k+j
k+j (cid:84)j−1E ,E(cid:48) ∀j >1 (cid:90) L (cid:90) L
i=1 k+i k+j P(C ) = 1− ··· N(y ;µ ,Σ )dy (5)
k d yd yd d
Fig. 1 illustrates the relationship between subevents S −L −L
k+j
and E , when d = 5. The event C can be represented
k+j k
as the union of disjoint subevents, S , or as the union of where
k+j
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 4
Fig.1. Level-CrossingEventRealization
Theorem1,whichcanbefoundinAppendixI,providesthe
    mathematical underpinnings for the optimal alarm condition
y 0
k+1 corresponding to the level-crossing event, shown here as
y =(cid:52)  .. , µ =0 = .. 
d  .  yd d  .  Eqn. 7. Alternatively, the optimal alarm condition derived in
y 0 Theorem 1 can be expressed in terms of the subevents E ,
k+d k+j
Σ =(cid:52) (cid:26) CPkC(cid:62)+R ∀i=j ∈[1,...,d] as shown in Eqn. 8.
yd CP C(cid:62) ∀j >i∈[1,...,d]
k+i,k+j
and P =(cid:52) Aj(P −PL)(A(cid:62))i+Aj−iPL
k+i,k+j k ss ss
We may approximate Σ as shown in Eqn. 6 by substitut-
yd
ing the steady-state version of the Lyapunov equation given
P(C |y ,...,y ) ≥ P (7)
previously as Eqn. 3, PL, in place of P , which agrees with k 0 k b
ss k d
our assumption of stationarity. (cid:92)
⇔P( E |y ,...,y ) ≤ 1−P (8)
k+j 0 k b
j=1
(cid:26) CPLC(cid:62)+R ∀i=j ∈[1,...,d]
Σ ≈ ss (6)
yd CAj−iPLC(cid:62) ∀j >i∈[1,...,d]
ss
This approximation, while it introduces error with regards
totheprobabilityofalevel-crossingevent,P(C )ataspecific The optimal alarm condition has therefore been derived
k
point in time, k, is ostensibly negligible and will provide for fromtheuseofthelikelihoodratioresultingintheconditional
a great computational advantage in the design of all alarm inequality as given in Eqn. 7. This basically says “give alarm
systems that it is based upon. Instead of designing an optimal whentheconditionalprobabilityoftheevent,C ,exceedsthe
k
alarm system for each time step, we design a single alarm levelP .”Here,P representssomeoptimallychosenborderor
b b
system based upon the limiting statistics that are reached at threshold probability with respect to a relevant alarm system
steady-state, greatly reducing the computational burden. The metric. It is necessary to find the alarm regions in order to
steady-stateassumptionhasnotbeenusedinworkbyAntunes design the alarm system. This alarm region is parameterized
etal.[13],butdoingsoalsoincursmuchgreatercomputational by future process output predictions and covariances, which
effort. can be derived from standard Kalman filter Eqns. 9 - 13.
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 5
(cid:90) L−yˆk+1|k (cid:90) L−yˆk+d|k
= ··· N(y ;0 ,Σˆ )dy (23)
d d yd d
yˆ = Cxˆ (9) −L−yˆk+1|k −L−yˆk+d|k
k|k k|k
where
xˆ = Axˆ (10)
k+1|k k|k
Fk+1|k =(cid:52) Pk+1|kCT(CPk+1|kCT +R)−1 (11)  yˆ 
k+1|k
Pk+1|k = APk|kAT +Q (12) yˆ =(cid:52) E[y |y ,...,y ]= .. 
d d 0 k  . 
P = P −F CP (13)
k+1|k+1 k+1|k k+1|k k+1|k yˆ
k+d|k
where Σˆ =(cid:52) (cid:26) Vk+i|k ∀i=j ∈[1,...,d]
yd CP C(cid:62) ∀i(cid:54)=j ∈[1,...,d]
k+i,k+j|k
xˆk|k =(cid:52) E[xk|y0,...,yk] Vk+i|k =(cid:52) CPk+i|kC(cid:62)+R
P =(cid:52) E[(x −xˆ )(x −xˆ )T|y ,...,y ]
k|k k k|k k k|k 0 k The feasible region for values of Pb can easily be de-
termined by applying an intermediate value theorem from
Relevant predictions, covariances and cross-covariances are
calculus which provides sufficient conditions for finding a
given below as Eqns. 14- 18, respectively.
levelsetsolution.ThesufficientconditionsareshownasEqns.
24-25, and the resulting level set is shown as Eqn. 26.
yˆ = CAjxˆ (14)
k+j|k k+j|k
P = Aj(P −PL)(A(cid:62))j +PL (15)
k+j|k k|k ss ss g(0 ) ≥ 1−P (24)
d b
≈ Aj(PˆR −PL)(A(cid:62))j +PL (16)
ss ss ss lim g(yˆ ) < 1−P , ∀j ∈[1,...,d] (25)
d b
Pk+i,k+j|k = Aj(Pk|k−PLss)(A(cid:62))i+Aj−iPLss(17) |yˆd|\yˆk+j|k→∞
≈ Aj(PˆR −PL)(A(cid:62))i+Aj−iPL (18) d
ss ss ss (cid:52) (cid:92)
PˆR = PR −F CPR (19) LA={ yˆk+j|k :g(yˆd)=1−Pb} (26)
ss ss ss ss
j=1
F = PRCT(CPRCT +R)−1 (20)
ss ss ss
Thenotationthatrepresentsthelimitingconditionshownin
PRss is the combined steady-state version of Eqns. 12 and Eqn.25is|yˆd|\yˆk+j|k →∞,andismeanttoindicatethatall
13givenpreviously,orthediscretealgebraicRiccatiequation, elements of yˆ other than yˆ approach ±∞. Application
d k+j|k
and PˆRss is the steady-state a posteriori covariance matrix of this condition yields Pb < 1, which is true by definition,
given in Eqn. 19. Eqn. 20 is also used in Eqn. 19, which and application of the sufficient condition shown in Eqn. 24
is the steady-state version of the Kalman gain from Eqn. 11. yields P ≥ 1 − g(0 ). Thus the feasible region for P is
b d b
The approximations shown in Eqns. 16 and 18 will provide P ∈[1−g(0 ),1].
b d
for a great computational advantage in design of the optimal It is not possible to obtain a closed-form representation of
alarmsystemanditscorrespondingapproximationsforreasons theparametrizationfortheoptimalalarmregionshowninEqn.
stated previously. Due to the approximation of Pk|k with PˆRss 21. As such, resulting ROC curve statistics can not be com-
shownintheseequations,theKalmanfilterwillbesuboptimal, putedanalyticallybymeansofnumericalintegrationaswillbe
ascitedbyLewis[16].However,theassumptionofstationarity shown to be possible for other methods. As an alternative, we
isrequiredforthedesignofanoptimalalarmsystemasdefined mustusetheMonteCarlostyleapproachdiscussedpreviously.
by Theorem 1, and holds here as well. This will alow for the ROC curve statistics to be estimated
A more formal representation of the optimal alarm region empirically with observational and truth data generated from
is shown in Eqn. 21, which essentially defines a sublevel set the existing model and corresponding simulations of level-
of g(yˆ )=(cid:52)P((cid:84)d E |y ,...,y ) as a function of yˆ . crossing events.
d j=1 k+j 0 k d
However, as will be shown, with the aid of two distinct
d approximations we can generate ROC curve statistics by
(cid:52) (cid:92)
A = { yˆ :P(C |y ,...,y )≥P } (21) numerically integrating expressions for the computation of
k k+i|k k 0 k b
i=1 relevant multivariate normal probabilities. These multivariate
d d probabilitycomputationsareperformedbyusinganadaptation
(cid:52) (cid:92) (cid:92)
= { yˆk+i|k :P( Ek+j|y0,...,yk)≤1−Pb} of Genz’s algorithm [17], which is based upon a robust and
i=1 j=1 computationally efficient technique designed to be used for
Eqns. 22-23 give the multivariate normal probability com- integrations in multiple dimensions for multivariate normal
putation to be performed via numerical integration, required distributions. This provides a tool necessary for the design
for enabling the optimal alarm condition. of approximations to an optimal alarm system, and also other
failuredetectionalgorithmssuchastheonemostoftenusedby
Kerr [18], who specifically cites issues with the computation
d (cid:90) L (cid:90) L
P((cid:92) E |y ,...,y )= ··· N(y ;yˆ ,Σˆ )dy of these types of integrals. As such, we can avoid otherwise
j=1 k+j 0 k −L −L d d yd d often very time and computationally intensive simulation runs
(22) when using Monte-Carlo style empirical estimation.
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 6
A. Root-finding Approximation
The optimal alarm region, A , can be approximated by
k
the alarm region specified by (cid:83)dj=1ΩAj. Fundamentally, the ΩAj = {yˆk+j|k :f(yˆk+j|k)≤1−Pb} (28)
approximationisconstructedbysolvingforasymptoticbounds = {|yˆk+j|k|≥LAj} (29)
on the exact alarm region. By using asymptotes, we are
implicitly making a geometrical approximation by forming where the root-finding problem is given by numerically
a hyperbox around the alarm region. Simple 2-dimensional solving Eqn. 30.
examples of such hyperboxes for various values of L, and
Pb are shown in Fig. 2. There is visual evidence that limiting L =(cid:52){|yˆ |:f(yˆ )=1−P } (30)
effectsforthisapproximationexist,asbothLandP approach Aj k+j|k k+j|k b
b
the extremities of their feasible ranges. These effects will be
Thus the root-finding approximation to the optimal alarm
touched on briefly later in the results section, but will be region is given by (cid:83)d Ω ≈A . Note that the function f
investigated in earnest in a sequel article. j=1 Aj k
incorporates all elements of the covariance matrix Σˆ when
yd
computing the asymptotes, just as when constructing the sub-
level set for the the exact optimal alarm region. Furthermore,
thefeasibleregionforP isidenticaltothesublevelsetofthe
b
exactoptimalalarmregion,P ∈[1−g(0 ),1]≡[1−f(0),1]
b d
by using a similar argument and set of sufficient conditions,
as shown in Eqns. 31-32 below.
f(0) ≥ 1−P (31)
b
lim f(yˆ ) < 1−P (32)
k+j|k b
|yˆk+j|k|→∞
However, there is one primary difference between this
approximation and exact alarm region. As far as the condi-
tional mean, yˆ , is concerned, the asymptotic approximation
d
is parameterized only by the corresponding dimension of the
conditionalmean,yˆ .Theexactoptimalalarmregionuses
k+j|k
all dimensions of the distribution and thus the conditional
mean, yˆ , simultaneously.
d
It is possible to generate formulae for the true and false
positive rates as a function of L by appealing to Eqns. 33-
Aj
34,whereinplaceofA itsapproximation(cid:83)d Ω maybe
k j=1 Aj
used.
True positive rate:
P(C ,A )
P =P(C |A ) = k k (33)
d k k P(A )
k
False positive rate:
Fig.2. Root-findingapproximationsforoptimalalarmregion P(C(cid:48),A )
P =P(A |C(cid:48)) = k k (34)
fa k k P(C(cid:48))
Mathematically, the approximation is formed by solving a k
P(A )−P(C ,A )
root-finding problem which yield bounding asymptotes. The = k k k
1−P(C )
root-finding problem is posed by first taking the limit as each k
dimension of Eqn. 21 approaches 0, other than the one for
BecausewehavealreadyintroducedtheformulaforP(C )
which the asymptote is being derived. Eqn. 27 expresses this k
in Eqn. 5, which holds regardless of the alarm system being
limiting condition as a function of the dimension of interest.
used, we must only find expressions for P(C ,A ) and
k k
(cid:52)
P(A ). They are given in Eqns. 35-36, where P =1 −
d k bcrit
f(yˆ )=(cid:52) lim P((cid:92) E |y ,...,y ) (27) g(0d)=1−f(0), and they are also implicitly expressed as a
k+j|k yˆd\yˆk+j|k→0 j=1 k+j 0 k functionofthedesignparameter,Pb,asaconsequenceofEqn.
30. Note also that the off-diagonal blocks of the covariance
Havingdefinedf(yˆ ),itisnowpossibletoexpressΩ matrix Σ are equivalent to Σˆ as a consequence of the
k+j|k Aj z yˆd
by Eqns. 28-29. projection theorem.
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 7
density whose conditional covariance matrix is given by Σˆ .
yd
(cid:26) P((cid:83)d Ω ) P >P The orthonormal decomposition of this covariance matrix and
P(Ak) = j=11 Aj Pb ≤Pbcrit (35) densityofthecorrespondingtransformedvectory˜d areshown
b bcrit in Eqns. 38 - 40.
(cid:26) 1−P((cid:84)d Ω(cid:48) ) P >P
= j=1 Aj b bcrit
1 P ≤P
b bcrit y˜ = Λy (38)
P(Ck,Ak)=(cid:26) P(Ck)−P(PA((cid:48)kC)+) P(Ck(cid:48),A(cid:48)k) PPb >≤PPbcrit Σˆydd = ΛΓdΛ(cid:62) (39)
k b b(3cr6it) N(yd;0d,Σˆyd) = N(y˜d;0d,Γ) (40)
where
Here, the elements of y˜ are independent, and thus Γ is
d
diagonal.Assuch,geometriccontainmenteasilyfollowswhen
P(A(cid:48))=P((cid:92)d Ω(cid:48) )=P((cid:92)d |yˆ |<L ) considering a revised expression for Ak and (cid:83)dj=1Ajk. Thus,
k Aj k+j|k Aj the latter approximation to the exact alarm region can be
j=1 j=1 rewritten in the transformed probability space as shown in
=(cid:90) LA1 ···(cid:90) LAd N(yˆ ;µ ,Σˆ )dy Eqn. 41. The superscript ∗ for all probabilities included in
d yd yˆd d this expression refers to the transformed values that results
−LA1 −LAd after the orthonormal rotation. Note that this expression does
and not change significantly from what was given in Eqn. 37.
Σˆ =(cid:52) Σ −Σˆ
yˆd yd yd
= O(PL −PˆR)O(cid:62) (cid:91)d (cid:91)d
ss ss Aj = {yˆ :P(E∗ |y˜ ,...,y˜ )≤1−P∗} (41)
 CA  k k+j|k k+j 0 k b
j=1 j=1
O =(cid:52)  ...  The exact alarm region A can be rewritten in the trans-
k
CAd formed probability space as shown in Eqn. 42, however the
expressionchangessignificantly,andinsuchamannertoallow
Furthermore,
for direct comparison to Eqn. 41.
d d
(cid:92) (cid:92)
P(C(cid:48),A(cid:48))=P( E , Ω(cid:48) )
k k k+j Aj d d
j=1 j=1 A ={(cid:92)yˆ :P((cid:92) E∗ |y˜ ,...,y˜ )≤1−P∗}
k k+i|k k+j 0 k b
(cid:90) L (cid:90) L (cid:90) LA1 (cid:90) LAd i=1 j=1
= ··· ··· N(z;µ ,Σ )dz
z z
−L −L −LA1 −LAd (cid:92)d (cid:89)d
={ yˆ : P(E∗ |y˜ ,...,y˜ )≤1−P∗} (42)
where k+i|k k+j 0 k b
(cid:20) (cid:21) i=1 j=1
z =(cid:52) yd
yˆ Because containment in this probability space is invariant
d
(cid:20) (cid:21) under orthonormal rotations, it follows from Eqns. 41- 42,
µ =(cid:52) µyd that (cid:83)d Aj ⊆ A , so that the approximate alarm region
z µ j=1 k k
yd is a proper subset of the exact alarm region. Fig. 3 provides
Σ =(cid:52) (cid:20) Σyd Σˆyˆd (cid:21) illustrative evidence of this containment in the transformed
z Σˆyˆd Σˆyˆd probability space when d=2. Here, the union of the red and
blue colored sections represents A (formula shown below)
k
B. Closed-form Approximation andthebluecoloredsectionrepresentstheapproximationA1∪
k
A2.
Theoptimalalarmregion,Ak,canalsobeapproximatedby k
an alarm region specified by (cid:83)d Aj, with a successive ap-
j=1 k
proximation on Aj; Aj is defined in Eqn. 37. Fundamentally, A = {(y˜ ,y˜ ):P(E∗ |y˜ ,...,y˜ )·
k k k k+1|k k+2|k k+1 0 k
the approximation can be constructed in the same fashion as P(E∗ |y˜ ,...,y˜ )≤1−P∗}
the root-finding method, by solving for asymptotic bounds on k+2 0 k b
the exact alarm region. A successive approximation is required in order to obtain
a closed-form representation and parametrization of the alarm
region without having to resort to root-finding required for
Aj ={yˆ :P(E |y ,...,y )≤1−P } (37)
k k+j|k k+j 0 k b solving P(E |y ,...,y )≤1−P , which is equivalent to
k+j 0 k b
Acontainmentrelationshipbetweentheexactoptimalalarm P(|yk+j| > L|y0,...,yk) ≥ Pb. This second approximation
regionandtheunionofinequalities(cid:83)d Aj ⊆A caneasily is given by Eqn. 43, which breaks this condition containing
j=1 k k
be shown with a linear transformation of the conditionally an absolute value into constitutive inequalities.
defined Gaussian vector y to a vector of independent vari-
d
ables. The integrand of Eqn. 23 is a multivariate Gaussian Ai,j ={yˆ :P(Ei(cid:48) |y ,...,y )≥P } (43)
k k+j|k k+j 0 k b
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 8
Fig.3. Containmentoftheapproximationbyexactalarmregion Fig.4. Closed-formapproximationinprobabilityspace
where The domain of feasibility for this approximation now
changes, and P takes on a new value, which differs from
bcrit
i ∈ B ≡{L,U} identical values of P = 1−g(0 ) and P = 1−f(0)
bcrit d bcrit
EU = {y <L} corresponding to the feasibility regions for the optimal alarm
k+j k+j
region and the root-finding approximation, respectively. A
EL = {y >−L}
k+j k+j derivation for the new value of P is provided in Eqns.
bcrit
Thus P(EU(cid:48) |y ,...,y ) + P(EL(cid:48) |y ,...,y ) ≥ P is 46-50 below. The derivation is based upon the premise that
k+j 0 k k+j 0 k b L >0,wherethelaststepfromEqn.49to50usesLemmas
approximated by two distinct inequalities given by the union Aj
of P(EU(cid:48) |y ,...,y ) ≥ P and P(EL(cid:48) |y ,...,y ) ≥ P . 2-5whichcanbefoundinAppendixI,andthefactthatR>0.
k+j 0 k b k+j 0 k b
ThissubsequentapproximationcaneasilybevisualizedinFig.
4. The union of the red and blue colored sections shown in L > 0 ∀j ∈[1,...,d] (46)
Aj
Fig.4,representsA1.Thusthebluecoloredsectionalonefrom (cid:113)
Fig. 4 is a subset okf this area, such that AU,1∪AL,1 ⊆ A1. L+ Vk+j|kΦ−1(Pb) > 0 ∀j ∈[1,...,d] (47)
k k k
If we replicate Fig. 4 for j ∈[1,...,d], then it becomes clear d (cid:32) (cid:33)
(cid:92) −L (cid:52)
that more generally Eqn. 44 holds, which summarizes all of Pb > Φ (cid:112)V =Pbj (48)
the containment relationships for the approximations covered j=1 k+j|k
in this subsection. Pbcrit > mjaxPbj (49)
(cid:32) (cid:33)
d d −L
(cid:91) (cid:91)Aik,j ⊆ (cid:91) Ajk ⊆Ak (44) = Φ (cid:112)Vk+d|k =Pbd (50)
j=1i∈B j=1
Again, by using asymptotes we implicitly make a geomet-
By using this successive approximation, we can now repre- rical approximation by forming a hyperbox around the alarm
sent the alarm region in “closed-form,” as shown in Eqn. 45 region. As before, simple 2-dimensional examples of such
below. hyperboxesforvariousvaluesofL,andP areshowninFig.5.
b
Furthermore,justasfortheroot-findingapproximation,visual
evidencethatlimitingeffectsforthisapproximationalsoexist,
(cid:91)d (cid:91) (cid:91)d (cid:113)
Aik,j = |yˆk+j|k|≥L+ Vk+j|kΦ−1(Pb)≡LAj as both L and Pb approach the extremities of their feasible
ranges. Note that both the approximation represented by Fig.
j=1i∈B j=1
(45) 3andthesuccessiveapproximationrepresentedbyFig.4have
Φ−1(·) represents the inverse cumulative normal standard been applied to yield the vector space result shown in Fig. 5.
distribution function, and L ∀j ∈ [1,...,d] represent the Both Figs. 3 and 5 have been illustrated for the case when
Aj
limitsofintegration.TheL valuescannowbeenre-defined d=2.
Aj
to replace the integration limits used for the root-finding Due to the containment relationship labeled Eqn. 44, qual-
method in Eqns. 33 - 36. As such, these same equations are itative arguments for the under-reporting of P and P can
d fa
valid for computing P and P in order to construct an be made for this approximation. A less aggressive, more opti-
d fa
ROC curve using this “closed-form” approximation as well. mistic strategy will result in comparison to the exact optimal
However, in place of A when using these equations, the method. It is unclear if this approximation will be more or
k
approximation (cid:83)d (cid:83) Ai,j is used. less accurate than the previous root-finding approximation.
j=1 i∈B k
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 9
(cid:90)
= N(y ;yˆ ,Σˆ )dy (52)
d d yd d
DΩ
(cid:90) L (cid:90) L−yˆk+j|k (cid:90) L
= ··· ··· N(y ;yˆ ,Σˆ )dy (53)
d d yd d
−L −L−yˆk+j|k −L
(cid:90)
P(E |y ,...,y )= N(y ;yˆ ,Σˆ )dy (54)
k+j 0 k d d yd d
DA
(cid:90) ∞ (cid:90) L−yˆk+j|k (cid:90) ∞
= ··· ··· N(y ;yˆ ,Σˆ )dy (55)
d d yd d
−∞ −L−yˆk+j|k −∞
where
X = {[−L,L]}⊂R
D = {Xd−1×[−L−yˆ ,L−yˆ ]}
Ω k+j|k k+j|k
D = {Rd−1×[−L−yˆ ,L−yˆ ]}
A k+j|k k+j|k
ItisclearthatD ⊆D duetothefactthatXd−1 ⊆Rd−1.
Ω A
As such, f(yˆ )≤P(E |y ,...,y ) easily follows due
k+j|k k+j 0 k
to the fact that both expressions share a common integrand.
It is therefore evident that our original claim Aj ⊆Ω , and
k Aj
thus (cid:83)d Aj ⊆(cid:83)d Ω is mathematically sound.
j=1 k j=1 Aj
According to this newly derived containment relationship,
and by again using qualitative arguments, it is clear that the
root-finding approximation will be more aggressive, and less
optimisticthantheclosedformapproximation.However,there
isnocontainmentrelationshipthatcanbeestablishedbetween
the root-finding method and the exact optimal alarm region as
could be performed for the closed form approximation. As
Fig.5. Closed-formapproximationsforoptimalalarmregion such, even though the root-finding method incorporates all
elementsofthecovariancematrixwhencomputingitsasymp-
totes, this approximation strategy may be overly aggressive
However, we do know that the off-diagonal elements of the
and overshoot the performance of the exact optimal method
covariancematrixΣˆ arenotusedforcomputingtheasymp-
yd under certain circumstances. This mathematical intuition will
totesofthis“closed-form”approximation.Recallthattheroot-
be supported by demonstrating this effect with examples later
finding method incorporates all elements of the covariance
in the results section.
matrixwhencomputingtheasymptotes.Yetbothmethodsuse
asymptotic approximations which are parameterized only by
C. Redline and Predictive Alarm Systems
the corresponding dimension of the conditional mean, yˆ .
k+j|k
As is apparent intuitively from Figs. 2 and 5, Aj ⊆ Ω , Thetwobaselinealarmsystemsmentionedpreviously(red-
k Aj
thus(cid:83)d Aj ⊆(cid:83)d Ω .Itisclearfromvisualcomparison line and predictive) will be compared to the optimal alarm
j=1 k j=1 Aj system and its approximations. All methods will attempt to
of these figures that this containment relationship exists be-
predictthelevel-crossingeventdefinedbyEqn.4.Theredline
tweentheroot-findingand“closed-form”approximations.For
alarm system attempts to define an envelope, [−L ,L ],
a mathematical proof of this containment, recall Eqns. 28-29 A A
outsideofwhichanalarmwillbetriggeredtoforewarnofthe
for Ω , shown again below, and compare them to Eqn. 37
for AjA,jalso shown again below. impending level-crossing event. The probabilities necessary
k to compute P and P based upon Eqns. 33-34 for this
d fa
alarmsystemareprovidedinEqns.56-59,wherewere-define
Ω = {yˆ :f(yˆ )≤1−P } A = {|y | > L }, such that the alarm is based only on the
Aj k+j|k k+j|k b k k A
current process value.
= {|yˆ |≥L }
k+j|k Aj
Aj = {yˆ :P(E |y ,...,y )≤1−P }
k k+j|k k+j 0 k b
P(A ) = P(|y |>L ) (56)
k k A
Ifwelookcloselyattheregionsofintegrationforf(yˆ )  
k+j|k
and P(Ek+j|y0,...,yk), as shown in Eqns. 51-55 below, we = 2Φ(cid:113) −LA  (57)
will notice that a clear containment relationship exists. CPLC+R
ss
P(C ,A ) = P(C )−P(A(cid:48))+P(C(cid:48),A(cid:48)) (58)
d k k k k k k
f(yˆk+j|k)= lim P((cid:92) Ek+j|y0,...,yk) (51) P(C(cid:48),A(cid:48)) = (cid:90) LA (cid:90) L ···(cid:90) L N(z;µ ,Σ )dz(59)
yˆd\yˆk+j|k→0 j=1 k k −LA −L −L z z
IEEETRANSACTIONSONINFORMATIONTHEORY,VOL.IT-XX,NO.X, XXX2010 10
where IV. EXAMPLE
The example to be used for the presentation of our results
(cid:20) (cid:21)
z =(cid:52) yk has no specific application, but is generic and based upon the
yd same example used by Svensson [2]. The model parameters
µ =(cid:52) (cid:20) µyk (cid:21)=0 are provided in Eqns. 64-67.
z µ d+1
yd
(cid:26) CPLC(cid:62)+R ∀i=j ∈[0,...,d] (cid:20) 0 1 (cid:21)
Σ ≈ ss A = (64)
z CAj−iPLC(cid:62) ∀j >i∈[0,...,d] −0.9 1.8
ss
(cid:2) (cid:3)
C = 0.5 1 (65)
The “redline” alarm system is termed as such in order to
(cid:20) (cid:21)
indicate that a simple alarm level crossing is used to predict 0 0
Q = (66)
a second more critical level-crossing. In this case two levels 0 1
are used, L as the failure threshold, and L as the design R = 0.08 (67)
A
threshold. For reasons stated earlier, this alarm system would
Unlessotherwisestated,allcasestobecomparedwillusea
be superior to a redline system that uses only a single level
threshold of L=16 while varying d, or a prediction window
L, even though predicted future process values are not used.
of d=5 while varying L.
The “predictive” alarm system does incorporate the use of
predictedfutureprocessvalues,anddefinesthesameenvelope,
[−L ,L ], outside of which an alarm will be triggered to V. RESULTS&DISCUSSION
A A
forewarn of the impending level-crossing event. However, the A comparison of the AUC for all alarm systems for a
alarm definition differs from the redline method, such that prediction window of d = 5 while varying L ∈ [2.89,17.83]
Ak = {|yˆk+d|k| > LA}. The predicted future process value is shown in Fig. 6.
yˆ is found from standard Kalman filter Eqn. 14. The
k+d|k
probabilities necessary to compute P and P based upon
d fa
Eqns. 33-34 for this alarm system are provided in Eqns. 60-
63.
P(A ) = P(|yˆ |>L ) (60)
k k+d|k A
(cid:18) (cid:19)
−L
= 2Φ √ A (61)
λ
a
P(C ,A ) = P(C )−P(A(cid:48))+P(C(cid:48),A(cid:48)) (62)
k k k k k k
(cid:90) L (cid:90) L (cid:90) LA
P(C(cid:48),A(cid:48)) = ··· N(z;µ ,Σ )dz(63)
k k z z
−L −L −LA
where
(cid:20) (cid:21)
z =(cid:52) yd
yˆ
k+d|k
(cid:20) (cid:21)
µ =(cid:52) µyd =0
z µ d+1
yˆk+d|k
Σ =(cid:52) (cid:20) Σyd Λ(cid:62)a (cid:21)
z Λ λ
a a
λ = CAd(PL −PˆR)(A(cid:62))dC(cid:62)
a ss ss
Λ = CAd(PL −PˆR)O(cid:62)
a ss ss
Note that λ and Λ have been derived with the aid of the
a a
projection theorem. All of the alarm systems described thus
far will be compared using the area under the ROC curve Fig.6. AUCforallalarmsystemsafunctionofcriticalthreshold,L
(AUC). This provides a performance metric that characterizes
theabilityofeachalarmsystemtoaccuratelypredictthelevel- It is very clear that the optimal alarm system and its
crossing event. The AUC has been deemed as a theoretically approximationsoutperformtheredlineandpredictivemethods,
valid metric for model selection and algorithmic comparison over the entire range of values shown for L, as expected.
[19]. The parameters of interest are L for the redline and Another important point to note is that the approximations
A
predictive methods, and P for the optimal alarm system shown as dashed and dash-dotted blue lines, approximate the
b
and its approximations. Results will follow in the subsequent exactoptimalperformance(insolidblue)quitewellovermost
section. of the range of values shown for L. However, as L → 0,