Table Of Content

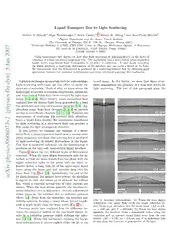
Liquid Transport Due to Light Scattering Robert D. Schroll,1 Régis Wunenburger,2 Alexis Casner,2,∗ Wendy W. Zhang,1 and Jean-Pierre Delville2 1Physics Department and the James Franck Institute, The University of Chicago, 929 E. 57th St., Chicago, Illinois 60637 7 2Université Bordeaux I; CNRS; UMR 5798, Centre de Physique Moléculaire Optique et Hertzienne, 0 351 cours de la Libération, 33405 Talence Cedex, France 0 (Dated: January 5, 2007) 2 Using experiments and theory, we show that light scattering by inhomogeneities in the index of n refractionofafluidcandrivealarge-scaleflow. Theexperimentusesanear-critical,phase-separated a liquid, which experiences large fluctuations in its index of refraction. A laser beam traversing J the liquid produces a large-scale deformation of the interface and can cause a liquid jet to form. 5 We demonstrate that the deformation is produced by a scattering-induced flow by obtaining good agreements between themeasured deformations and those calculated assuming this mechanism. ] n y Aphotonexchangesmomentumwithitssurroundings. broad hump. In this Letter, we show that these struc- d - Light-scattering techniques use this effect to probe the tures demonstrate the presence of a bulk flow driven by u structureofmaterials. Muchofwhatweknowaboutthe light scattering. The rest of this paragraph gives the l f mesoscopicstructuresincolloidalsuspensions,emulsions, . s and near-critical fluids have been revealed by light scat- c tering [1, 2, 3, 4]. More recently, many researchers have i s exploredhowthe intenselightbeamgeneratedbyalaser y canaccelerateandtrapmicron-sizedparticles[5,6]. Ap- h p plications range from laser tweezers [7, 8, 9] to particle [ sortinginmicrofluidicchannels[10,11,12]. Howeverone consequence of scattering has received little attention. 2 v Since a liquid flows readily, the momentum transferred 3 by light scattering in a structured fluid can produce a 7 flow along the light propagationdirection. 0 In this Letter, we examine one example of a struc- 6 tured fluid, a phase-separatedliquid near a second-order 0 6 phasetransition,andshowthatastrongflowisproduced 0 by light-scattering off density fluctuations in the liquid. / This flow is measured indirectly via the deformations it s c produces on the very soft, near-critical liquid interface. i s Figure 1 shows the two different types of deformation y observed. When the laser shines downwardsonto the in- h terface,sothatthebeamtravelsfromthephasewiththe p higher refractive index to the phase with the lower re- : v fractive index, a long, thin jet of the upper-layer liquid i X forms along the beam axis and intrudes deep into the lower fluid [Fig. 1(a)] [13]. Sporadically, the end of the r a jetshedsdroplets. Formodestlaserpowers,theshedding is regular in time and allows us to measure the volume flux, which is typically several tens of cubic microns per second. When the laser shines upwards,the interface re- mainsunbrokenevenathighpower. Instead,adownward tether forms on the interface due to radiation pressure effects [14]. Away from the centerline, the interface also FIG. 1: Interface deformations. (a) When the laser shines deflects upwards, forming a hump whose lateral length- downwards, the upper fluid (with the larger refractive in- scale is much larger than the beam width [Fig. 1(b)]. dex) forms a jet intruding into the lower layer. (∆T = 6K, Previous works have analyzed how the difference be- ω0 = 3.47µm, and P = 490mW) (b) When the laser shines tween the refractive indices of the two liquid phases re- upwards, the interface forms a downwards tether along the sults in a radiation pressure which deforms the inter- centerline and an upward, broad hump away from the cen- face [13, 15]. While this mechanism explains the beam- terline. (∆T =1.5K, ω0 =4.8µm, and P as indicated) The sizeddeformations,itcannotexplaineitherthejetorthe arrows show thedirection of propagation of the laser. 2 40 30 20 ) m µ FIG. 2: Toroidal recirculation produced in the lower layer ( when the laser shines from below. The hump height is typi- h 10 cally around 10µm, while the fluid layer is 1mm thick. The dotted box indicates thearea seen in thephotographs. 0 key points of our argument, which are also illustrated in Fig. 2. We begin with the simpler question of how a −10 broad hump is created when the interface is illuminated −50 0 50 from below. Light scattering produces an upwards body r (µm) force on the liquid within the laser beam, driving an up- wardsflowwithin the litregion. By conservationoffluid FIG. 3: Hump profiles for P =592mW (upper profiles) and mass,thisflowisreplenishedbyadownwardsflow. Inthe for296mW(lowerprofiles). ω0 =4.8µm(blackdots),5.3µm, experiment,andinmostsituationsofinterest,inertialef- 6.3µm, 7.5µm, 8.9µm, 11.7µm, and 15.3µm (lightest gray dots) and ∆T = 1.5K for all profiles. Away from the beam fects are negligible. Since purely viscous flows minimize axis,alloftheprofilesfallontothesameshape,demonstrating dissipation[16], the replenishingflow takes the formof a that only the laser power, and not the light intensity, affects single toroidal recirculation. Viscous stresses associated thelarge-scale humpshape. withtherecirculationdeformtheinterfaceupwards. This creates a hump whose width corresponds to the size of the recirculation and is therefore much wider than the strength of the light-induced flow, depends on the light laser beam. In the rest of the paper, we show that the intensity. The momentum per unit volume transferred qualitative scenario described above can quantitatively from the laser beam into the liquid via scattering is pro- account for the broad hump shapes measured. In addi- portional to the beam intensity I. Therefore the body tion, we estimate the volume flux of flow driven by the force Fv is also proportional to I. This body force acts lightinthe jetting regimeandfindreasonableagreement as a pressure gradient along the beam axis. Balancing with the measured values. Fv againstviscous resistanceµu0/ω02, where we use the The fluid used in the experiments is a water-in-oilmi- beamwidthω0asacharacteristiclengthscaleofthelight- cellar fluid at a critical composition. Above the critical induced flow, yields ◦ temperature T 35 C, the fluid separates into two im- c ≈ u0 Iω02/µ P/µ. (1) miscible phases with different micelle volume density Φ, ∝ ∝ in a second-order phase transition [17]. Near the critical Thisargumentpredicts,counter-intuitively,thattheflow temperature, many physical properties scale like power strength has no dependence on the beam intensity. It laws in ∆T T Tc. For our purpose, the most im- only depends on the beam power. If this is true, then ≡ − portantscalingbehavior is the divergenceofthe osmotic the interfacedeformationcreatedby theflowshouldalso compressibility, χT ∆T−1.24. The fluid experiences havenodependenceonthelightintensity. Figure3shows ∝ fluctuations in its order parameter,Φ, which act as light two sets of measured hump profiles. Each set is taken scatterers. These fluctuations have a correlation length at a fixed beam power, with the different profiles corre- ξ− ∆T−0.63,whichistypicallyhundredsofAngstroms. spondingtodifferentbeamsizes. Remarkably,consistent ∝ The very weak absorption of light at the laser frequency with the prediction (1), the hump shape away from the (αth =3 10−4cm−1) ensures that laser heating is neg- center remains the same for different beam widths when × ligible. The fluid is enclosed in a thermally controlled the power is held constant. In contrast, the downward- fused quartz cell (2 10 40mm3). Optical forcing is pointing tether at the center of the hump, previously × × provided by a linearly polarized TEM00 continuous Ar+ shown to be created by radiation pressure, varies with laser, with a vacuum wavelength of λ = 5145˚A and a the beam width. beam power P < 2W. The beam has a Gaussian profile Next, we explicitly calculate the shape of the inter- withwidthω0,varyingfrom3µmto15µm. Moredetails face deformation as a function of P and ∆T and com- about the experiment can be found in [15]. pare the calculated shapes with the measured shapes. We can construct a simple argument for how u , the This requires us to first relate u , which characterizes 0 0 3 the strength of the recirculation, to the laser power P, and then to relate the shape deformation to u . 0 Toobtainu (P),wenotethateachscatteringoffaden- 0 z u sity fluctuation transfers momentum to the fluid. Sum- 0 mingtheindividualcontributionsfromallfluctuationsin a unit volume gives the body force: 0 0.1 0.2 0.3 0.4 r/r Fv =DχT I, (2) 0 where D describes the interaction of the light with the FIG. 4: Form of the vertical velocity uz at the mid-plane of densityfluctuationsandisgivenby π3n Φ∂ǫ 2 k Tα−4 the fluid layer, from the flow model. The layer aspect ratio λ4 c ∂Φ T B 8α3+2α2+2α 2α2+2α+1 ln(cid:0)(1+2(cid:1)α) . Here, (depth/radius= L/r0) is 1/5. α×(cid:2)3 2(2πnξ−/λ)2 −an(cid:0)d n = √ǫ is(cid:1)the index o(cid:3)f refrac- ≡ tion. This result comes from a calculation analogous to Finally,werelatetheinterfacedeformationh(r)tothe the turbidity calculation by Puglielli and Ford [18, 19]. viscous stresses σ associated with the toroidal recircu- zz Since the correlation length is shorter than the wave- lation, and therefore to the laser power P. Because the length of light in the regime examined, the fluctuations capillarylengthscalegoesto0nearT ,buoyancyisasim- c act as Rayleigh scatterers. The calculation also assumes portant as surface tension in resisting the deformation. single scattering,whichis justified by the largeturbidity The steady-state interface h(r) is therefore given by length. Combining this resultwith the balancefrom(1), we see DχTP 2γκ(r)+∆ρgh(r)=σ C g(r,r /L), (4) zz 0 ≡ L u =CF ω 2/µ=CDχ P/µ, (3) 0 v 0 T whereκ(r)isthemeancurvatureoftheinterface. Todis- where C is an undetermined numerical prefactor depen- play the various dependencies of σ , we have rewritten zz dantonthe details ofthe couplingofthe light-scattering itintermsofadimensionalstressandtwodimensionless forcetothelarge-scaleflows. ThevelocityscaleDχ P/µ quantities, the constant C and the function g(r,r /L) T 0 is roughly tens of microns per second for experimental describing the radial decay of the stress. The boundary conditions. conditionatthewallofcylindricalcellish(r )=0. Near 0 We next relate the flow within the region illuminated the centerline, the interface develops a downward tether bythelaserbeamtothelarge-scalerecirculatingflowre- due to radiation pressure. We account for this O(ω ) 0 sponsible for the broad hump. The liquid in the lower tetherbyimposingthe boundaryconditiondh/dr=0at layer lies within a cylindrical cell of radius r and depth r =ω , which mimics the observed circular rim, created 0 0 L. Since the laser beam width is much narrower than by radiation effects which are not included here. the width of the recirculation, we represent the light- Numericalsolutionsof(4)atdifferentlaserpowersare induced flow as simply a point force along the centerline displayed in Fig. 5, together with experimentally mea- of a cylindrical cell. Also, as the interface deformations sured interface profiles at the same laser powers. Values are much smaller than the scale of the flow, we treat ofthematerialparametersandbeamsizeusedinthecal- the interface between the layers as perfectly flat. These culationaretakenfromtheexperiment. Thevalueofthe simplificationsallowustoobtainananalyticsolutionfor unknown constant C is fixed at 33 by requiring that the the bulk flow. In our model, the single toroidal recir- maximumheightofthecalculatedshapeequalsthemea- culation corresponds to an eigenfunction which satisfies sured shape at P =592mW. This is the only fitting ad- no-slipboundary conditions on the side wallsof the con- justment we have made between the calculation and the tainerandfree-stressboundaryconditionsonthetopand measurement. Theagreementbetweenthemeasuredand bottom surfaces of the container. The top and bottom thecalculatedinterfaceshapesisexcellent. Comparisons boundary conditions are not consistent with the experi- atlarger∆T fora rangeofpowersproducedgoodagree- mentalsituation. Howevertheerrorintroducedprimarily ment as well, although the smaller size of the hump at affects the absolute scale for the strength of the recircu- larger ∆T makes detailed comparisons less precise. This lation,whichcontrolsthe absolutescaleforthe heightof behavior in ∆T rules out thermocapillary flows, used to the interface deformation. It has little effect on the rela- drive drop motion in previous studies [20], which vanish tive shape ofthe deformationorhow itchangeswith the close to the critical point. laser power P or the temperature T, which are the as- We next consider the liquid transport inside the jet. pects we focus onwhen we comparethe calculationwith While the complexity of the pattern of light propaga- the measurements. Figure 4 plots the vertical velocity tion at the interface prevents a detailed comparison be- u (r) in the middle of the liquid layer. Note the flow is tween the calculation and the measurements, it is pos- z upwards at small r and downwards near the side-wall, sible to obtain a rough estimate. Since the jet radius consistent with the sketch in Fig. 2. r is observed to increase weakly with the beam power j 4 such an effect has been used to transport individual col- 40 loidal particles whose size is comparable with the beam width [21], the possibility of transporting smaller col- 35 loidalparticlescollectivelyhasnotbeennotedbeforeand is worth further investigation. 30 25 The authors thank B. Issenmann for providing exper- ) imental data on the jet. This work was supported by a m µ 20 National Science Foundation Graduate ResearchFellow- ( h ship (RDS), NSF MRSEC DMR-0213745 (U. Chicago), 15 andtheCentreNationaldelaRechercheScientifiqueand Conseil Régionald’Aquitaine. 10 5 0 ∗ Presentaddress: Commissariatàl’EnergieAtomique,BP −50 0 50 12, 91680 Bruyères-le-Châtel, France r (µm) [1] B.J.Ackerson,C.M.Sorensen,R.C.Mockler,andW.J. O’Sullivan, Phys. Rev.Lett. 34, 1371 (1975). FIG. 5: The calculated (solid line) and experimental (dots) [2] D. J. Pine, D. A. Weitz, P. M. Chaikin, and E. Her- hump profile for ∆T = 1.5K, ω0 =4.8µm. From bottom to bolzheimer, Phys. Rev.Lett. 60, 1134 (1988). top, P =88.8, 177.6, 296.0, 414.4, and 592.0 mW. [3] B. J. Berne and R. Pecora, Dynamic Light Scattering (DoverPublications, 2000). [4] W. van Megen and S. M. Underwood, Phys. Rev. E 47, 248 (1993). andisalwayslessthanthebeamsizeω ,weassumesim- 0 [5] A. Ashkin,Proc. Natl. Acad. Sci. USA94, 4853 (1997). ply that the power of the light trapped inside the jet [6] J. Xu, J. Drelich, and E. M. Nadgorny, Langmuir 20, is 2P(r 2/ω 2), a fraction of the incident beam power. j 0 1021 (2004). Given the beam power inside the jet and (3), the trans- [7] A. Terray, J. Oakey, and D. W. M. Marr, Science 296, port flux is 1841 (2002). [8] D. G. Grier, Nature 424, 810 (2003). Q=u0πrj2 ≈2πC DχµTP (cid:18)ωrj42(cid:19). (5) [9] JD.. HEnangestro,rpM,.LaGbo.kCsöhrip, 4K,.19R6a(m2s0e0r4,).P. Hagberg, and 0 [10] M.P.MacDonald,G.C.Spalding,andK.Dholakia,Na- This estimate gives the right order of magnitude for the ture 426, 421 (2003). volume flux. For example, an experiment with P = [11] M. Ozkan, M. Wang, C. Ozkan, R. Flynn, A. Birkbeck, and S.Esener, Biomed. Microdevices 5, 61 (2003). 473.6mW at ∆T = 4K and ω = 5.08µm yields a jet 0 [12] S. Neale, M. P. MacDonald, K. Dholakia, and T. F. with roughly 1 µm radius and measured volume flux of Krauss, NatureMaterials 4, 530 (2005). 110µm3/s. The estimate (5) gives 310µm3/s. [13] A.CasnerandJ.-P.Delville,Phys.Rev.Lett.90,144503 In conclusion, we have used a combination of experi- (2003). mentandtheorytodemonstratethatlight-scatteringcan [14] A.Casner,J.-P.Delville,andI.Brevik,J.Opt.Soc.Am. produceasignificantflowinastructuredfluid. Intheex- B 20, 2355 (2003). [15] A.CasnerandJ.-P.Delville,Phys.Rev.Lett.87,054503 periment, we measure the large-scale interface deforma- (2001). tion and the liquid transport produced by illumination [16] G. K. Batchelor, An Introduction to Fluid Dynamics ofanintenselaser. Toshowthatthedeformationisare- (Cambridge University,1967). sultoflight-inducedflow,wecompareinterfacedeforma- [17] Although the fluid is a quaternary mixture, the phase tions calculatedbasedonthe light-scatteringmechanism transitionbelongstothe(d=3,n=1)universalityclass against measured deformations. Excellent agreements of the Ising model [E. Freysz, E. Laffon, J.-P. Delville, are found between the calculated and the measured de- and A.Ducasse, Phys.Rev.E 49, 2141 (1994)]. formations. We emphasize that such light-induced flows [18] V. G.Puglielli andN.C. Ford, Jr., Phys.Rev.Lett. 25, 143 (1970). exist whenever fluids have mesoscopic spatial variation [19] L. S. Ornstein and F. Zernike, Proc. Kon. Ned. Akad. in the refractive index and do not require the fluid to Wetensch. 17, 793 (1914). be near a second-order phase transition. For example, a [20] N. Garnier, R. O. Grigoriev, and M. F. Schatz, Phys. suspension of 100 nm-diameter glass beads in water at Rev. Lett.91, 054501 (2003). 10% volume fraction would experience a scattering force [21] S. J. Hart and A. V. Terray, Appl. Phys. Lett. 83, 5316 5 times larger than is seen in our experiment. While (2003).