Table Of Content

Draftversion January31,2012 PreprinttypesetusingLATEXstyleemulateapjv.5/2/11 LINE PROFILES OF CORES WITHIN CLUSTERS: I. THE ANATOMY OF A FILAMENT Rowan J. Smith and Rahul Shetty Zentrumfu¨rAstronomiederUniversitätHeidelberg,Institutfu¨rTheoretischeAstrophysik,Albert-Ueberle-Str. 2,69120Heidelberg, Germany Amelia M. Stutz Max-Planck-Institutfu¨rAstronomie,Königstuhl17,D-69117Heidelberg,Germany 2 1 and 0 Ralf S. Klessen 2 Zentrumfu¨rAstronomiederUniversitätHeidelberg,Institutfu¨rTheoretischeAstrophysik,Albert-Ueberle-Str. 2,69120Heidelberg, Germany n Draft version January 31, 2012 a J ABSTRACT 0 Observations are revealing the ubiquity of filamentary structures in molecular clouds. As cores are 3 often embedded in filaments, it is important to understand how line profiles from such systems differ fromthoseofisolatedcores. Weperformradiativetransfercalculationsonahydrodynamicsimulation ] A ofa molecularcloud inorderto modelline emissionfromcollapsingcoresembedded in filaments. We model two optically thick lines, CS(2-1) and HCN(1-0), and one optically thin line, N H+(1-0), from G 2 three embedded cores. In the hydrodynamic simulation, gas self-gravity, turbulence, and bulk flows h. create filamentary regions within which cores form. Though the filaments have large dispersions, the p N2H+(1-0) lines indicate subsonic velocities within the cores. We find that the observed optically - thick line profiles of CS(2-1) and HCN(1-0) vary drastically with viewing angle. In over 50% of o viewing angles, there is no sign of a blue asymmetry, an idealised signature of infall motions in an r isolated spherical collapsing core. Profiles which primarily trace the cores, with little contribution t s from the surrounding filament, are characterisedby a systematically higher HCN(1-0) peak intensity. a The N H+(1-0) lines do not follow this trend. We demonstrate that red asymmetric profiles are also [ 2 feasibleintheopticallythicklines,duetoemissionfromthefilamentorone-sidedaccretionflowsonto 1 the core. We conclude that embedded cores may frequently undergo collapse without showing a blue v asymmetric profile, and that observational surveys including filamentary regions may underestimate 5 the number of collapsing cores if based solely on profile shapes of optically thick lines. 7 Subject headings: Stars: formation, ISM:structure, kinematics and dynamics, lines and bands 2 6 1. 1. INTRODUCTION (2009)foundthatasymmetriescanbe foundonscalesas small as 1000 AU. In this work we will revisit the asym- 0 Star-forming regions are complex systems observed 2 projected onto the plane of the sky. Therefore it has metric collapse profile using simulations of star cluster 1 alwaysbeenadifficulttasktodeterminethetruegeome- formation within a large molecular cloud. This paper : tries and dynamics within them. One key tool for disen- examinesthe caseofirregularcoresembeddedwithinfil- v aments,andfutureworkwillconsiderthecaseofmassive i tanglingthetruedynamicalstateofstar-formingcoresis X the blue infall asymmetry. This effect (Zhou et al. 1991; star-forming regions. Zhou (1992) calculated the line profiles expected to r Zhou 1992; Walker et al. 1994; Myers et al. 1996) relies a on the fact that within a collapsing core there is both a arise from an inside-out Shu (1977) collapse and from Larson-Penston collapse (Larson 1969; Penston 1969). centrallyincreasingdensity profile,andtwo pointsalong Both models produced an asymmetric collapse profile, a line of sight with the same velocity. In optically thick and the resulting line-widths could be used to distin- species (τ >1) only the foregroundgas at a givenveloc- guish between the two collapse profiles. A follow up ity is visible. This leads to an asymmetry in the double- study (Zhou et al. 1993) showed that the line profile of peaked emission line profile as the visible blue emission the near-spherical Bok globule B335 matched their ex- from the far side of the core originates from higher den- pected Shu collapse profile. This result was initally con- sity gas. The blue infall asymmetry was derived under firmedbyChoi et al.(1995),butlaterstudieshaveshown the assumption of spherical symmetry. that more complex models may actually be needed (e.g. However,observationsincreasinglyshowthatthisisan Wilner et al. 2000; Stutz et al. 2008). Other variants of ideal rarely achieved in molecular clouds. For instance, collapse models have been studied. Walker et al. (1994) André et al. (2010) showthat star-formingcoresare fre- carriedoutlinemodellingofprolatecollapsingcores,not quently part of filaments, Bontemps et al. (2010) ob- just spheres, and once again found blue asymmetric line servedthatmassivestar-formingregionscontainmultiple profiles. Myers et al.(1996)usedasimpleanalyticmodel substructures, and Tobin et al. (2010) and Stutz et al. oftwoconverginglayersofgasandproducedthesamere- sult. The study of sphericalcoreline profileshas contin- [email protected] 2 Smith et al. uedinmorerecentyears. InparticularRawlings & Yates In a collapsing spherical core (2001), Tsamis et al. (2008) and Stahler & Yen (2010) have shown the importance of accurately modelling the chemicalabundances within cores,particularly since op- ticallythick carbonbearingspecies,suchasCOandCS, θ' θ'' freeze out within the dense core centres (Tafalla et al. 2002). Are these models sufficiently accurate to capture the behaviour of realistic star-forming cores? One potential difficulty is that for cores embedded at the end of a collapsing filament or other complex structure, accretion onto the core may predominantly occur from just The line-of-sight densities and velocities are... one direction, as seen in Smith et al. (2011). This may lead to either a blue or red asymmetry depending on whichside ofthe corethe accretionflowis located. Sim- LOS velocity density ilarly,morecomplexmorphologiesandinternalvelocities within the filamentand surroundingenvelopecouldlead toself-absorptionintheenvelopeobscuringthevelocities from the core. Investigations into numerical simulations Line-of-sight have demonstrated that the structures identified in syn- thetic maps or position-position-velocity cubes may not necessarily correspond to contiguous structures in three dimensionalspace,duetothegeometricprojectionalong thelineofsight(e.g. Pichardo et al.2000;Ostriker et al. In optically thick species only the nearest point at any velocity is seen. 2001; Shetty et al. 2010). Cores embedded within filaments are a common fea- tureofmolecularclouds,asshownbyrecentHerschel ob- self-absorption servations(Arzoumanian et al.2011;Men’shchikov et al. 2010; André et al. 2010). Moreover, in Smith et al. nsity (2011) we specifically studied the geometryof the small- nte i est scales of collapsing ‘Class 0’ cores from a molecular cloud simulation, and found that even on scales of a ∼ 1000 AU, the cores were irregular, extended struc- -v 0 +v tures. The only way to understand the effects of a fila- velocity mentarygeometryonresultingemissionlineprofilesisto Denser material emits at a greater intensity. directly test these scenarios with radiative transfer line modelling. Fig. 1.— A schematic showing the origin of a blue asymmetric lineprofilefromasphericallysymmetriccollapsingcore. Despitethemanycomplicatingfactors,blueasymmet- ric collapse profiles are often observed. Gregersen et al. (1997) observed a sample of 23 Class 0 sources and towards the centre, however, we only observe the veloc- found blue asymmetric line profiles in 9 cases, com- ity component projected along the line of sight. Figure pared to 3 sources with a red asymmetry. Similarly, 1 shows how the angle (θ) between the sightline and the ‘blue’ cores have been found in surveys by Lee et al. corecentreincreasesalongthelineofsight. Farfromthe (1999), Gregersen & Evans (2000), Wu & Evans (2003) core centre the angle is small and so the velocity com- and Fuller et al. (2005). On the other hand, while these ponent along the line of sight is large. However,close to surveys find potential infall candidates, the majority of the core centre the observed velocity component is zero. the cores do not have a blue asymmetric profile. The Conversely, the absolute magnitude of the velocity in- questionis,couldagreaterfractionofcoresbecollapsing creases towards the centre of the core. For a core with than what is inferred by blue asymmetric line profiles? a velocity profile shallower than v ∝ r−1 this results in r We focus on the line profiles arising from collapsing therebeing twopositions alongthe line ofsightwith the coresembeddedwithintheirregularfilamentsfromwhich same projected velocity. they are formed. The layout of this paper is as follows. For an optically thin line (τ < 1) all the emission di- In Section 2 we describe in more detail the physical ef- rectedtowardstheobserverisvisibleandaGaussianpro- fectswhichleadtoablue-peakedasymmetriclineprofile. file is observed. However,for an optically thick emission InSection3wedescribeourmethodsandmodels,andin line (τ >1) only the nearest point at a given velocity is Section4weoutline ourresults,payingparticularatten- detected. In a spherical collapsing core this means that tion to the viewing angle of the model. In Section 5 we onthered-shiftedsideofthecore,theouterlayersofthe discusshowourresultsmayaidinterpretationofobserva- core are seen, but on the blue-shifted side, the central tions. FinallyinSection6wesummariseourconclusions. regions are seen. For an emission line with a high criticaldensity, there will be more emissioncoming from the 2. ANASYMMETRICLINEPROFILE core centre than from the outer layers of the core and Figure1showsaschematicdescribingtheoriginofthe consequently, the intensity is higher in the blue part of blue line asymmetry in the simple case of spherical col- the line than the red part. The resulting line, therefore, lapsingcore (see alsoEvans 1999). The gasfalls radially has a central dip where the low velocity envelope ob- Line Profiles from Filaments 3 scures the core, and two peaks from the collapsing core, densities above this value. The filaments in which the of which the blue peak is more intense. coresareembeddedhavenumberdensitiesof5×103cm−3 The density and velocity profiles shown in the middle to 3 × 104cm−3. They are themselves surrounded by panel of Figure 1 are the key requirement to produce a even more tenuous material, with densities of 103cm−3 blue asymmetric profile. The question is, are these line or lower. of sight profiles present in filamentary collapsing cores? We model the emission from a 0.4 pc box centred on the collapsing core. The original SPH simulation is in- 3. METHOD terpolatedto agridwitha cellsizeof2×10−3 pc. Fora coreat a distance of 150pc this correspondsto a resolu- 3.1. Filamentary core models tion of around 2.8 arcseconds. However,the line profiles For our models of filamentary cores we use data from are measured over a Gaussian beam with a full width agiantmolecularcloud(GMC)simulationthathasbeen half maximum (FWHM) of 0.01pc, which corresponds the basis of much of our recent work on star formation. to 13.7 arcseconds. The models are selected at a time FordetailsofthissimulationseeSmith et al.(2009a). In period where the central core has just started collapsing Smith et al. (2011) we found that ‘Class 0’ cores from and a sink particle is about to form in the simulation. this simulation had filamentary features on scales as In observational parlance the cores could be considered small as a few thousand AU. In fact, in only ∼ 25% of asstarlessobjects thatareabouttobegintheir ‘Class0’ cases could the cores truly be consideredspherical. This phase of core evolution. haspotentiallyinterestingconsequencesforcorelinepro- Inordertomakeacomparisontoobservationaldatawe files, because, as discussed in the Introduction, previous estimatethemassofthefilamentsbycalculatingthetotal models generally assumed spherical symmetry. massofgasinourgridmodelswithadensityintherange Ouroriginalsimulationusedatemperatureparameter- 5×103cm−3<n<3×104cm−3. ForFilamentsA,Band isation(see Smith et al. 2009b) which producedtemper- C we obtain values of 6.4 M⊙ , 12.3 M⊙ and 14.7 M⊙ atures of around 10K in the dense gas (n>104 cm−3), respectively. Hacar & Tafalla (2011) find values in the and temperatures of up to 60K in the most diffuse gas range4.8 M⊙ to11.3 M⊙ forfourfilamentstheystudied (n < 102 cm−3). This includes a heating term based in L1517. Our values are therefore in good agreement onthe YSOmodels ofRobitaille et al.(2006)thatis ap- with the masses of observed filaments. plied in the vicinity of sink particles (which represent Furthermore, we also find good agreement when com- the locations of star formation). In order to verify that paring our simulation to observed column densities in the original temperature distribution of our simulation star-forming regions. The bottom panel of Figure 2 wasnotthe majorcauseofthe line profilebehaviour,we showsacolumndensityprojectionfromtheoriginalsim- re-ran one of our models with a constant gas tempera- ulation of each filament before radiative transfer, which ture of 14K. The only noticeable change in the result has been smoothed as if observed by a 0.01pc width was that the central brightness temperatures were one Gaussian beam. The column densities of our filaments degree higher; the qualitative behaviour of the lines did are in the range 1022 −1023 cm−2 with a typical col- not change. umn density of around 4×1022 cm−2, and an increase We select three typical regions from the GMC simu- incolumndensity atthe locationofthe denseembedded lation each containing a core embedded within a larger cores. Men’shchikov et al. (2010) find column densities filament. Thecoresareidentifiedfromlocationsoffuture in the range 5×1020−1.4×1023 cm−2 for filaments in sink-particle formation, and consequently our sample is Aquila,andcolumndensitiesof3×1020−8.6×1021 cm−2 biased as it contains only cores which truly are collaps- for filaments in Polaris. Our filaments resemble dense ing. We choose to select our cores in this manner so filaments in Aquila far more than the Polaris filaments. that we can 1) identify collapsing cores and 2) under- This is reasonable as they are extracted from a simu- stand how reliably we can determine this when the core lation undergoing rapid star formation like that seen in isembeddedinadensefilament. Themodelsarelabeled theAquilafield. ThePolarisregioncontainsnoclearex- FilamentsA,BandC(forreferenceFilamentBcontains amplesofpre-stellarcores(Ward-Thompson et al.2010). the filamentary core shown in Figure 1c of Smith et al. In conclusion our model filaments closest observational 2011). Figure 2 shows the 850 µm dust emission calcu- analogue is to dense star-forming filaments in clustered latedfromeachfilament. FilamentsAandCarealigned regions rather than diffuse quiescent filaments. paralleltotheaxisofthemodelgrid,andeachcontainsa secondembedded core besides the centralone. Filament 3.2. Molecular line modeling A is a turbulent sheet. Filament B is an interface where We use the radiative transfer code RADMC-3D 1 to fast-moving diffuse gas collides with slow-moving dense carry out the line modelling of the cores. RADMC-3D gas, and has a more curved geometry. Filament C is a models a variety of radiative processes including dust head-oncolliding flow. These regionsshowmarkedsimi- thermalemissionandabsorption,dustscattering,aswell laritiestorecentHerschel observations(e.g.André et al. as gas atomic and molecular lines. It is this latter capa- 2010; Men’shchikov et al. 2010). We discuss the dynam- bility which is of importance here. ics and formation mechanisms of the filaments in more Thechemicalspecieswhichwewillconsiderinthispa- detail in Section 4.2. per have emission lines with high critical densities and Inallthreecases,theembeddedcorecontainsgaswith densities of 3 ×104cm−3 to 107cm−3. However when 1 This code is publicly available with the permis- averagedacrossaGaussianbeamofhalf-width0.01pcthe sion of the author, Cornelius Dullemond, at the website maximum observed core density decreases to 106cm−3, http://www.ita.uni-heidelberg.de/dullemond/software/radmc-3d/. as only a small percentage of the gas in the beam has Apaperdescribingitsusageiscurrentlyinpreparation. 4 Smith et al. Fig.2.—Top Thethreefilaments in850µm dustemission. Middle TheemissionfromFilamentAforeach species. Bottom Acolumn densityprojectionoftheoriginalsimulationbeforeradiativetransfer,whichhasbeensmoothedasifobservedbya0.01pcGaussianbeam as such are typically not in local thermal equilibrium mayoccuratmorethanonepositionandsotheassump- (LTE).Consequently,anon-LTEapproachmustbeused tion of LVG is not fully satisfied. However, Ossenkopf for the line transfer. We use the large velocity gradient (1997) showed that the Sobolev approximation can be (LVG) approximation (Sobolev 1957) which uses local used in regimes where it does not strictly apply, such velocity gradients to define photon escape probabilities. as turbulent flows in molecular clouds, and still yield Fora full descriptionofhow LVGhasbeen implemented reasonably accurate results. In spherical homogeneous in RADMC-3D see Shetty et al. (2011a, a). We also flows like the idealised case shown in Figure 2, he found use a method known as ‘Doppler catching’ to interpo- thatthe errorhada maximumvalue ofonly20%. More- late under-resolved velocities along each line of sight as over this error was mainly in the line intensity, rather described in Shetty et al. (2011b, b) than in the shape of the line profile. We test this fur- In the cores studied here a given line of sight velocity ther by calculating the LTE line profiles for our cores Line Profiles from Filaments 5 and then comparing them to the LVG results. In LTE core centre. Therefore we will use the simple constant themaximumintensitiesarehigherduetotheartificially abundance model and leave a more detailed analysis of high level populations. However, both methods show a the N H+ chemistry to future works. 2 dip at the same velocity in the line profile, and so we The second molecular tracer is CS, which is optically can be confident that our assumption of LVG is not af- thick and traces the more diffuse gas in the envelope fecting the qualitative behaviour of the lines. We also around the core. Molecular collisional rates and Ein- tested our method using a completely spherical collaps- stein coefficients for CS were calculated by Turner et al. ingcoreforanopticallythickspeciesandconfirmedthat (1992). We model the 2-1 transition of CS, which has the expected blue asymmetric line profile was produced a rest frequency of 98.981 GHz. The critical density of in agreement with previous studies. CS is n = 3.2×105 cm−3 at a collisional tempera- crit ture of 20K. As an optically thick line, CS exhibits self- 3.3. Molecular Species absorptionand is capable of producing a blue asymmet- The general procedure for creating the molecular line ric collapse profile. The classic work on infall signatures profiles is the following. The filaments from our original by Zhou (1992) used CS. However, Tafalla et al. (2002) simulationare mapped onto a grid and the number den- showed that CS is depleted at the centre of cores due to sity of each desired species is calculated using simplified its freezing onto dust grains. They found the depletion prescriptionsfortheabundancesasafunctionofdensity. could be described by an abundance prescription The gridsareusedas inputs forRADMC-3D, whichcal- culates the level populations of the tracer species, and A (r)=A e−n(r)/nd (1) CS 0 then carries out ray-tracing to calculate the molecular emission. Tocomputethe levelpopulationsofourchem- where A is the abundance, and n is the H number CS 2 ical species we use line data obtained from the Leiden density. We adopt values of n = 2×104cm−3 for the d LAMDA database (Schoïer et al. 2005) and assume that depletion density and A =4×10−9 for the low density 0 molecular hydrogen is the dominant collisional partner. abundance limit, based on the typical values given in Weconsiderthreemolecularspeciesinthisstudy,each Tafalla et al. (2002). Stahler & Yen (2010) recently car- havingdifferentpropertiesandtracingdifferentregimes, ried out line modelling of diffuse cores with and without as shown in Table 1. The chosen line transitions all lie CS depletion, and found that the models with depletion withinthe observablerangeofmostgroundbaseddetec- were a better match to observations, and so we adopt tors, such as ALMA. All transitions have a high critical it here. Due to depletion the number density of CS is density, and hence are dense gas tracers. Consequently, almost negligible in the densest regions of our cores. any differences in the emitted line profiles are primarily ThethirdmolecularspeciesweconsiderisHCN,which due to optical depth effects. is optically thick and traces the dense gas. The col- The isolated component of N2H+ is optically thin and lisional rates for this species have been calculated by tracestheentiretyofthedensegas. Molecularcollisional Green & Thaddeus (1974) and Dumouchel et al. (2010). ratesandthetheEinsteincoefficientsofthisspecieshave HCN is particularly useful because it has three well- beencalculatedbyDaniel et al.(2005)andSchoïer et al. separatedhyperfineemissionlineswithinits1-0leveland (2005). N2H+ hassevenhyperfinelines thatmakeupits eachonehasslightlydifferentopticaldepths,withF(0-1) (1-0)transition. Wemodeltheisolated101-012hyperfine being the optically thinnest, F(2-1) the optically thick- line,whichhasarestfrequencyof93.176GHz. Thecrit- est,andF(1-1)intermediateinopticaldepth. Sohn et al. ical density for LTE is estimated to be ncrit =1.4×105 (2007)haverecentlypointedouttheutilityofthisspecies cm−3, using the relation ncrit = Aul/Kul where Aul is as a diagnostic tracer of infall motions in dense cores the Einstein A coefficient and Kul is the collisional rate and as such it is the key tracer we consider here for (at an assumed kinetic temperature of 20K). As the iso- our filamentary cores. We use a constant abundance of lated hyperfine line of N2H+ is optically thin it contains AHCN =3×10−9 for the molecular abundance of HCN, informationaboutallthevelocitiesalongthelineofsight following Lee et al. (2004). Note that some variation in andnoasymmetricinfallsignatureisexpected. Nonethe- abundanceisseenincorecentresbyLee et al.(2004)but less, this line is a useful reference when comparedto op- forsimplicity weneglectthis here. The restfrequencyof ticallythick lines to separateself-absorptioneffects from the central HCN hyperfine line is 88.632 GHz. intrinsic variation in the velocity profiles. To check that the cores are visible through the fila- We calculate the abundance of N2H+ using the re- ment, we first calculate the dust emission in RADMC- sults of Aikawa et al. (2005) who find an abundance of 3D,usinga dust-to-gasratioof0.01andaconstantdust A = 10−10 relative to the H number density of temperature of 20K. Figure 2 shows that the embedded N2H+ 2 the gas. The abundance of N H+ has been proposed to cores can be clearly seen in 850 µm dust emission. 2 rise when CO is frozen onto dust grains as CO destroys The line models are calculated for each molecular N H+. For instance Jørgensen et al. (2004) found that speciesat256evenly-spacedwavelengths,centredonthe 2 asCObecomesdepletedontodustgrainsthe abundance rest wavelength of the relevant emission line. The bot- ofN H+ increasesto A=10−8. However,when we used tompanels of Figure 2 show the emissionfrom Filament 2 this value for the N H+ abundance above the CO freeze A at the rest wavelength for each of the three species 2 outdensityofn=3×104cm−3 (Bergin & Tafalla2007), (forHCNweshowtheF(2-1)hyperfineline). TheN H+ 2 wefoundthattheN H+ emissionbecametoobrightand emissionismainly fromthe densegastracedbythe dust 2 optically thick compared to its observed behaviour. In emission,whereasthe CSshowsmore extended emission Aikawa et al.(2005) the N H+ abundances incollapsing from the surrounding filament. The HCN emission is 2 Bonnor-Ebertspheresshowedvariationsofatmostafac- bright in both the cores and the surrounding regions. tor of a few, and a slight decrease in abundance at the The second core, to the left of the central core, actually 6 Smith et al. TABLE 1 The propertiesof the molecular tracers. The criticaldensity for LTE isestimated using the relation nH2 =Aul/Kul where Aul is the Einstein AcoefficientandKul isthe collisional rate coefficientatan assumedkinetic temperatureof 20K. Tacer Line Criticaldensity Optically AbundanceLaw N2H+ 1-0 [1c.m4−×31]05 thin 1[n0/−n1H02] CS 2-1 3.2×105 thick 4×10−9e−nH2/nd (nd =4×104 cm−3) HCN 1-0 2.6×106 thick 3×10−9 Generally the lines have more emission in their wings when observed in CS and HCN than in N H+ emission. 2 ThebottompanelofFigure2showstheemissionineach species from this filament. Due to their higher abundances, the emission from CS and HCN extends beyond the densest parts of the filament. This greater contribution of material from the outer edges of the filament increases the apparent line width of the core. The fila- mentvelocitieswillbediscussedinmoredetailinSection 3. 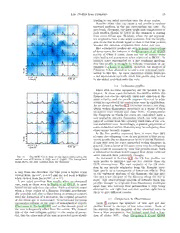Figure 4 shows a single viewing angle corresponding to an inclination and rotation of zero in our co-ordinate system. However, in such a filamentary and complex environment, the gas properties are likely to vary along Fig.3.— The number density of CS (dotted line) and the gas eachsightline. ThisisexaminedinFigures5and6which numberdensity(solidline)measuredalongalinethroughthecore shows the HCN F(2-1) hyperfine line at various viewing centre. There is a sharp rise in density at the location of the collapsing core (at a number density of around 3×104 cm−3). anglesaroundthe filaments; the CS(2-1)lines are shown However at these densities the CS is frozen out and so it only in Figures 7 and 8. In the left hand panels of the fig- tracesthesurroundingfilament. ures the model is kept a the default rotation, φ=0◦, and we view the model at 45◦ intervals in inclination. In appearsbrightersinceitismoreevolvedandhasahigher the right hand panels, we keep a constant inclination of temperature. inc=90◦ andview the model at45◦ intervalsin rotation. The abundance of CS is lower in the core centre than We sample a total of 14 unique lines of sight through in the surrounding filament due to the effects of freeze each core centre. out (outlined in the previous Section). Figure 3 shows It is immediately apparent that there is a large de- thenumberdensityofCSandthegasdensityalongaline greeofvariabilityamongthe coreline profilesdepending through the core centre. The densest regions of the core on the viewing angle. Importantly, this is also true of are effectively not contributing to the CS emission. The sight-lines which pass through the same material but in HCN and N2H+, however, follow the gas distribution. the opposite direction. For example, the HCN lines at Thegasdensitiesareextremelylowoutsidethefilament, inc=0◦ and inc=180◦ in Filament A pass through the but increases steadily in the filament, and rises sharply same gaseous regions but in the opposite direction, yet atthecenteroftheembeddedcore. Asthedensityofthe the former has a blue asymmetric profile and the latter gasissolowattheedgesofourbox,wecanbeconfident a red. Even more striking examples in Filament A are that we are integrating over the full length scale from the phi=90◦ and inc=270◦ sight-lines which do not even which there are contributions to the total emission. sharethesamegeneralshape. Thisvariabilityintheline profiles has immediate unfortunate implications for the 4. RESULTS interpretationoftheopticallythicklineprofilesforcores 4.1. Line Profiles embeddedwithinfilaments. Ifasimpledynamicalmodel (for instance that of a collapsing Bonnor-Ebert sphere) InFigure4weshowthelineprofilesofthecentralcore were used to predict observationalline profiles, very dif- of Filament A, calculated for a beam with a FWHM of ferent interpretations of the dynamical state of this core 0.01pc. The beam passes directly through the centre of would be deduced, purely due to line-of-sight effects. It thecoreandisviewedatamodelinclinationandrotation of zero. The dotted lines show the line profile of N H+. is worthstating againthat the corein the centre of each As N H+ is optically thin, allthe emissionis visible2and filament is the same regardless of viewing angle. 2 Figure 5 contains sight-lines which show the expected the line profiles are generally Gaussian. This confirms blue asymmetry, but the majority of cases have no clear that deviations from this profile in the other lines are asymmetryatall. Thereareevenafewcasesthatdisplay due to optical depth effects. a red asymmetry. A red profile is commonly taken as a InFigure4theCSprofileshowsaslightredasymmetry signatureofcoreexpansion,oroscillation(e.gKeto et al. rather than a blue one as the blue emission has been 2006) as the reversed velocity field means that the red largelyself-absorbed. However,higherintensityemission portionofthelineprofileoriginatesfromthehigherden- is seenfromthe blue side ofthe HCN F(2-1)line profile. sity part of a spherical core. Table 2 shows the total ThethinnerF(0-1)lineshowsonlyashoulderonthe red number of visible blue and red asymmetries in the HCN side of a central peak, whereas the F(2-1) hyperfine line F(2-1) for our three embedded cores. We classify the gives a clearer blue asymmetric profile. Line Profiles from Filaments 7 Fig. 4.—Theemissionlineprofilesfromtheembedded coreatthe centreofFilamentAcalculated usingasimulated0.01pchalf-width beam through the centre of the core. The dotted lines show the N2H+(1-0) optically thin line emission from the core. Higher intensity emissionisseenfromthebluesideoftheHCNF(2-1)lineprofilewhenthemodelisseenfromthisviewingangle. culated by the equation TABLE 2 Asummaryofthe classification types assignedto the δV =(V −V )/∆V (2) HCNF(2-1) linesfromfilamentsA,BandC usingthe line thick thin thin profileshapes. Despite the factthatthe embedded cores where ∆V is the full width half maximum (FWHM) are collapsing, a blueasymmetricline profile isseen in thin of the optically thin line. We calculate this value for the only 36%of cases. isolatedHCN hyperfine line andfor the CS(2-1)lines by Filament Blue Red Ambiguous fitting a Gaussianprofile to the N H+ line to obtain the 2 A 5/14 4/14 5/14 line centre and FWHM. We then find on which side of B 7/14 2/14 5/14 theN H+ linecentretheopticallythicktracerpeaksand 2 C 3/14 1/14 10/14 fit a Gaussian to this component to obtain the optically Total 15/42 7/42 20/42 thick component. Figure 9 shows the results of these 36% 17% 47% calculations. A negative value of δV is blue shifted and a positive cores as blue when there was a clear peak in the blue value red shifted. An observation is considered to be side of the profile and a clear lower intensity peak or a detection of true infall or expansion if |δV| is greater shoulderinthe red. Whenthe moreintensepeakwason than 5σ(δV). For HCN, 20/42 (48%) of the line profiles the red side of the profile, we classify the core as red. If are classified as blue shifted collapse profiles, and 13/42 both peaks were of a similar intensity, two clear peaks (31%)ofthelineprofilesareredexpansionprofiles. This could not be distinguished within the line, or there was is slightly higher than in the above classificationby pro- only one clear peak, the line profile is classified as being file shape as some of the profiles previously classified as ambiguous. ambiguousare nowclassifiedascollapsingorexpanding. For HCN under half of the line profiles are blue, with It is interesting to note in Figure 9 that there is a gap atotalof35%ofthesight-linesshowingthis asymmetry. in the distribution around the zero point. This could be Of the remainder, 17% of sight-lines show a red asym- either due to statistical effects or that our sample is bi- metry, and 48% of cases show no clear asymmetry. For ased as it only contains dynamical collapsing cores and CStheinterpretationisevenmorecomplicatedasthere- not any static cores. sultinglineprofileismainlydeterminedbythedynamics TheδV distributionforCS(2-1)isveryslightlyskewed of the filamentary envelope surrounding the core (since towardstheblueside. ForCSthereare16/42(38%)pro- molecularfreezeoutofCSontodustgrainsleadstovery files where δV is indicative of collapse and 14/42 (33%) low abundances at the core centre, as shown in Figure where δV is indicative of expansion. In addition to the 3). Figure 7 shows that the CS line profiles are as likely highfalsepositiverateofredprofiles,manyoftheGaus- to show a red asymmetric profile as a blue asymmetry sian fits to the CS(2-1) lines are too poor for the core and that the majority of the lines are hard to interpret, to be classified. As in the case of the above classifica- particularly in filaments A and C. Park & Hong (1998) tionbyprofileshape,theCS(2-1)lineisapoorindicator showed that underlying ‘clumpiness’ within a core can of collapse for cores embedded in dense dynamical fila- flattenthe resultingline profilesandsuperposesmallve- ments. Given these detection statistics, it is clear that locity features onto the line where the maximum clump the velocities that the CS traces are largelyunrelated to velocities lie. This complicates the interpretation of the those within the dense core. Subsequently, we shall fo- lineprofileinirregulardensityfields,suchasthoseinour cusontheHCNlines. Assuchwearetakingtheoptimal models,andinsomeextremecasescanevenleadtofalse case for detecting a blue asymmetric line profile from a infall expansion signatures. In our models we find only collapsing core. six line profiles which clearly resemble classical infall or All of the filaments contain a collapsing core, yet in expansionprofilesinthe CSsample,three(7%)red,and morethan50%ofcases,ineventhemostsensitivetracer three (7%) blue. (HCN),thiscollapsedoesnotrevealitselfasablueasym- Analternativemethodofclassifyingcoresistousethe metry in the line profile. This leads us to the first con- normalised velocity difference δV between the optically clusionofthisstudy: filamentscanobscuresignaturesof thick and thin lines (Mardones et al. 1997). This is cal- collapse from their embedded cores. 8 Smith et al. Fig.5.— The HCN F(2-1) line profiles of Filaments A (top), B (bottom) at different viewing angles. The central colour image of each panelshowsthedustdensityintheplaneinwhichthesight-linespassthroughthecore. Thebackgroundgrey-scaleimagesshowthelarge scale(0.4pcdiameter)dustemissionmapofthefilamentwhenviewedatthelabeledangle. Thepositionatwhichtheouterimagestouch thecentralimagedenotes theorientationofthesightline. Thelineprofilesofthecentralcoreateachangleareover-plottedontopofthe greyscale image. A coloured dot shows how the profilewas classified. Thelineprofiles arecalculated fora 0.01pc beam centred directly on the embedded core. In the left hand panels the rotation angle has a constant value of φ=0◦, and in the right panels the inclination hasaconstant valueofinc=90◦ 4.2. Velocity structure of the filament the main sites where turbulent energy is transferred from large scales to small. For example, Boldyrev et al. Given the importance of the dynamical state of the (2002) extended the She & Leveque (1994) model of in- envelope on the resulting core line profile, we examine compressible turbulence to the supersonic compressible in more detail the dynamics of the filaments. Figure regime and found that making the assumption that dis- 10 shows the velocity field in three slices that intersect sipation occurred in micro-turbulent sheets achieved a the core in Filament A, and a zoom into the centre of good agreement with numerical simulations. More re- the x-y plane. Filament A is a turbulent sheet with a cently, Schmidt et al. (2008) analysed high resolution disordered velocity field within the x-y plane. There is turbulent boxes with various forcing scales and found no systematic velocity along the filament’s major axis, thatthe mostdissipativestructuresareintermediate be- andthereareseveralregionsthatarecontracting. Inthe tween filamentary and sheet-like structures. Therefore y-z and x-z planes the diffuse material surrounding the it is to be expected that shocks will dissipate energy filament has a clearer systematic velocity gradientand a andtransformturbulencefromhighamplitudelargescale larger absolute velocity. motionsinthediffusegasintomanylowamplitudesmall Sheets and filaments are well known to be one of scale motions within the denser filament. The velocities Line Profiles from Filaments 9 Fig.6.—TheHCNF(2-1)lineprofilesofFilamentCatdifferentviewingangles. AsinFigure5. shown in Figure 10 are therefore a natural consequence have a much more disordered velocity field (see also of filament formation from a turbulent molecular cloud. Klessen et al. 2000). The zoom in to the central core of Filament A shown The effect that these disorderedvelocities in the plane in Figure 10c shows the detailed velocity structure sur- of the filament have on the line profiles is illustrated in roundingthecentralembeddedcore. Inthiscasetheflow Figure 12, indicating the velocities and densities of the onto the central core is not radially symmetric, but in- materialalongthe inc=0◦,phi=0◦ lineofsight(this cor- steadthere aretwisting streamsofmaterialflowingonto respondstothe-zaxisshowninFigures10and11). This thecore. Behindthecorethereisevenastagnationpoint figure provides examples of how the physical conditions in the velocity field (similar effects have been seen in in Figures 10 and 11 gave rise to the line profiles shown Ballesteros-Paredeset al. 2003 and Klessen et al. 2005). in Figure 5. Anysightlinewhichpassesthroughthisstagnationpoint The left panel of Figure 12 shows Filament A. Along willdiffersubstantiallyfromthetheoreticalvelocitypro- this line of sight the stagnationpoint is behind the core, file shown in Figure 1. so there are no blue-shifted velocities. In other words, Figure 11 shows a slice through Filaments B and C most of the mass the core accretion occurs from one di- in a similar manner to Figure 10. In Filament B a fast rection. Consequently, when viewed from the forwards moving flow of gas is pushing against a denser region of direction(inc=0◦), the densest visible peak in the veloc- gas with lower mean velocities. The dense filament is ity profile is on the blue side and when viewed from the found at the interface of the two regions and along this the reversedirection(inc=180◦) the densestvisible peak boundaryturbulentwhorlsofgascanbeseen. Alongthis is on the red side. This gives rise to a profile which is interface material from the fast-moving diffuse flow will either red or blue asymmetric depending on the viewing shockontothesurfaceofthefilament. FilamentCisonce angle. again formed at the interface between two flows. In this ThecentralpanelofFigure12showsFilamentB.Here case, however, the contrast is even more extreme as the thevelocityprofileinthe coreissimilartothatobserved flows are converging. Both flows are supersonic which in Figure 1. However, the region as a whole exhibits will lead to a rapid accumulation of dense material at a large scale velocity gradient as the filament is swept their interface. along with a larger external gas flow. On the forward Clearlythevelocitiesinthefilamentswithinwhichthe (inc=0◦) side, the optically thick emission comes from cores are embedded are very different from the quies- thedensestpointoftheblue-shiftedvelocities,andablue cent enveloped envisage in Section 2. Moreover, these asymmetric profile is produced. However on the reverse velocity flows are an intrinsic part of the filament as sidethereisopticallythickemissionatthesamevelocity they result as a byproduct of its formation. Indeed it in front of the core. This obscures the blue-shifted core hasbeenproposedthatgravitationalcontractionandac- emission, and so no blue asymmetry is seen. cretion are drivers of turbulence on virtually all scales TherightpanelofFigure12showsFilamentC.Inthis (Klessen & Hennebelle 2010). Many previous discus- filament the velocity profile of the collapsing core joins sions of filamentary geometries in the literature have fo- smoothly on to the large scale convergent motions that cussedoneither hydrostaticfilaments (Ostriker1964)or are forming the filament. Here the converging gas flows their subsequent self-similar collapse (Hennebelle 2003; firstbringthe filamenttogether,andthenathigherden- Tilley & Pudritz2003). ThefilamentsinourlargeGMC sities gravity leads to the formation of a dense core (see simulations are dynamic objects that form as a result also Hennebelle & Chabrier 2008; Banerjee et al. 2009). of turbulence and the associated shocks, and therefore When viewed from the reverse direction (inc=180◦) the 10 Smith et al. Fig.7.—AsinFigure5butforthecaseofCS(2-1)emission. gas distribution in front of the core does not overlap in sions. Thevolume weighteddispersionis largerthanthe velocity space with the central core. Consequently all density weighted value, as expected from the fact that the optically thick emission from the core is visible to the core forms at the stagnation point of a convergent theobserver,andthereisneitheraselfabsorptiondipat flow. To illustrate this, Figure 13 shows a histogram of thecentreofthelineprofile,noranyasymmetrybetween thesimulationvelocitiesatequallyspacedintervalsalong the blue and red side of the line. the beam for the filaments. In the case of Filaments B and C the velocity distribution is non-Gaussian and ap- 4.3. Line-widths pearsbimodal, whichreflectsthe convergingflowsofgas around the filament. In Figure 13 we also plot two sub- Another interesting diagnostic is the linewidths of the sets of the data; points with densities above 104 cm−3, N H+ profiles. Table 3 shows the mean velocity disper- 2 andpoints above105 cm−3. Bothsubsets occupy a nar- sion,σ(v),oftheN H+ lineswhenfittedbythefollowing 2 rower velocity range than the parent distribution, and Gaussian function the velocity range of the 105 cm−3gas which is associ- −(v−v )2 ated with the cores typically is around the sonic scale. 0 G=A0exp(cid:20) 2σ2(v) (cid:21) (3) Thisexplainswhythe‘observed’N2H+ linewidthsofthe cores are roughly sonic. where A is the peak line brightness and v the rest ve- That the velocity dispersions found from the N H+ 0 0 2 locity. Table3alsoliststhe velocitydispersionalongthe lines are typically coherent is in good agreement with beam directly from the model. We calculate both the recent observational studies of star-forming filaments. volume weighted and density weighted velocity disper-