Influence of spontaneous emission on a single-state atom interferometer

13 Pages·2008·0.46 MB·English

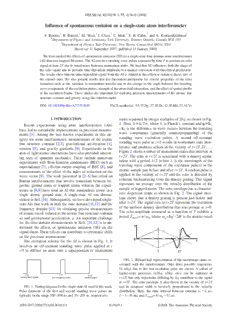
PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
Influence of spontaneous emission on a single-state atom interferometer
S. Beattie,1 B. Barrett,1 M. Weel,1 I. Chan,1 C. Mok,1 S. B. Cahn,2 and A. Kumarakrishnan1
1DepartmentofPhysicsandAstronomy,YorkUniversity,Toronto,Ontario,CanadaM3J1P3
2DepartmentofPhysics,YaleUniversity,NewHaven,Connecticut06511,USA
(cid:1)Received12September2007;published15January2008(cid:2)
Wehavestudiedtheeffectsofspontaneousemission(cid:1)SE(cid:2)onasingle-statetimedomainatominterferometer
(cid:1)AI(cid:2)thatusestrappedRbatoms.TheAIusestwostandingwavepulsesseparatedbytimeTtoproduceanecho
signalattime2Tduetointerferencebetweenmomentumstates.WefindthatSEinfluencesboththeshapeof
theechosignalanditsperiodictime-dependentamplitudeinamannerconsistentwiththeoreticalpredictions.
Theresultsshowthatthetime-dependentsignalfromtheAIisrelatedtotheeffectiveradiativedecayrateof
the excited state. We also present results that test theoretical predictions for several properties of the echo
formation such as the variation in momentum transfer due to the change in the angle between the traveling
wavecomponentsoftheexcitationpulses,strengthoftheatom-fieldinteraction,andtheeffectofspatialprofile
of the excitation beams. These studies are important for realizing precision measurements of the atomic fine
structureconstantandgravityusingthisinterferometer.
DOI:10.1103/PhysRevA.77.013610 PACSnumber(cid:1)s(cid:2): 03.75.Dg,37.10.De,42.50.Md,37.10.Vz
I.INTRODUCTION statesseparatedbyintegermultiplesof2(cid:2)q,asshowninFig.
Recent experiments using atom interferometers (cid:1)AIs(cid:2) 2. Here, (cid:2)(cid:5)h/2(cid:3), where h is Planck’s constant and q(cid:5)k1
−k is the difference in wave vectors between the traveling
have led to remarkable improvements in precision measure- 2
ments (cid:3)1(cid:4). Among the best known experiments in this cat- wave components (cid:1)generally counterpropagating(cid:2) of the
standing wave excitation pulses. A second off-resonant
egory are atom interferometric measurements of the atomic
fine structure constant (cid:3)2,3(cid:4), gravitational acceleration (cid:3)4(cid:4), standing wave pulse at t=T results in momentum state inter-
rotation (cid:3)5(cid:4), and gravity gradients (cid:3)6(cid:4). Experiments in the ference and produces echoes in the vicinity of t=2T,3T,....
Figure2showsasubsetofmomentumstatesthatinterfereat
area of light-matter interactions have also provided interest-
t=2T. The echo at t=2T is associated with a density modu-
ing tests of quantum mechanics. These include numerous
experiments with Bose-Einstein condensates (cid:1)BEC(cid:2) such as lation with a period (cid:4)/2 (cid:1)where (cid:4) is the wavelength of the
superradiance (cid:3)7(cid:4), efficient output coupling of BEC (cid:3)8(cid:4), and traveling wave components of the excitation pulses(cid:2) in the
atomicsamplejustbeforeandaftert=2T.Areadoutpulseis
measurements of the effect of the index of refraction on the
wave vector (cid:3)9(cid:4). The work presented in (cid:3)2–6(cid:4) has relied on applied in the vicinity of t=2T and the echo is detected by
coherentbackscatteringfromthedensitygrating.Thissignal
Raman interferometers that involve transitions between hy-
represents an average over the velocity distribution of the
perfine ground states of trapped atoms whereas the experi-
ments in (cid:3)8,9(cid:4) have used anAI that manipulates atoms in a sampleoftrappedatoms.Theechoenvelopehasacharacter-
istic dispersion shape as shown in Fig. 2. The signal enve-
single atomic ground state. A single-state AI was demon-
stratedinRef.(cid:3)10(cid:4).Subsequently,wehavedevelopedsingle- lope shows that a density grating is present just before and
stateAIs that work in both the time domain (cid:3)11,12(cid:4) and the aftert=2T.Thesignalzeroatt=2T representstherecreation
frequency domain (cid:3)13(cid:4) for obtaining precise measurements of the uniform density distribution that was present at t=0.
ofatomicrecoil(cid:1)relatedtotheatomicfinestructureconstant The echo amplitude measured as a function of T exhibits a
(cid:1)(cid:2) and gravitational acceleration, g.An important challenge period Trecoil=(cid:3)/(cid:5)q, where (cid:5)q=(cid:2)q2/2M is the atomic recoil
for the time domain measurements in Refs. (cid:3)11,12(cid:4) is to un-
(cid:4)(cid:4)
derstand the effects of spontaneous emission (cid:1)SE(cid:2) on the
signalshape.Theseeffectscancontributetosystematicshifts
on the precision measurement.
(cid:3)(cid:3)
The excitation scheme for the AI is shown in Fig. 1. It (cid:5)(cid:5)
involves an off-resonant standing wave pulse applied at t
=0 to diffract an atom into a superposition of momentum (cid:2) (cid:1)(cid:2)
FIG. 2. Billiard ball representation of the momentum states as-
sociated with the interferometer. Only three possible trajectories
(cid:1)0,±(cid:2)q(cid:2) due to the first excitation pulse are shown. A subset of
higher-order processes (cid:1)±2(cid:2)q, ±3(cid:2)q, etc.(cid:2) can be rephased at
(cid:3)(cid:17)(cid:18) (cid:3)(cid:17)(cid:19) (cid:3)(cid:17)(cid:14)(cid:19)
(cid:1)(cid:2)(cid:3)(cid:4)(cid:5)(cid:6)(cid:7)(cid:3)(cid:8)(cid:3)(cid:7)(cid:9)(cid:10)(cid:11)(cid:12)(cid:13)(cid:2)(cid:4) (cid:14)(cid:10)(cid:15)(cid:4)(cid:5)(cid:6)(cid:7)(cid:3)(cid:8)(cid:3)(cid:7)(cid:9)(cid:10)(cid:11)(cid:12)(cid:13)(cid:2)(cid:4) (cid:16)(cid:4)(cid:8)(cid:15)(cid:9)(cid:12)(cid:3)(cid:11)(cid:12)(cid:13)(cid:2)(cid:4) t=2T, but only trajectories differing by (cid:2)q contribute to the signal
at t=2T. The echo envelope is also shown in the vicinity of t=2T
FIG.1. Timingdiagramforthesingle-stateAIusedinthiswork. and its temporal width is inversely proportional to the velocity
Pulse durations of the first and second standing wave pulses are distribution. Here, the time interval between extrema is (cid:6)2(cid:6)s,
typicallyintherange500–800nsand30–200ns,respectively. T(cid:6)1–30ms,andT =(cid:3)/(cid:5)(cid:6)32(cid:6)s.
recoil q
1050-2947/2008/77(cid:1)1(cid:2)/013610(cid:1)13(cid:2) 013610-1 ©2008TheAmericanPhysicalSociety
BEATTIEetal. PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
frequency, and M is the atomic mass. The recoil period can (cid:22)(cid:7)(cid:16)(cid:3)(cid:12)(cid:8)(cid:13) (cid:21)(cid:3)(cid:8)(cid:3)(cid:4)
beunderstoodphysicallyasthetimetakenforawavepacket
traveling with recoil velocity (cid:2)q/M to move through one (cid:20)(cid:5)(cid:6)(cid:7)(cid:3)(cid:4)(cid:15) (cid:21)(cid:3)(cid:8)(cid:3)(cid:4)
period(cid:1)(cid:4)/2(cid:2)ofthedensitygrating.Aprecisionmeasurement
of (cid:2)/M can be obtained by measuring the periodic echo (cid:1) (cid:1)
amplitude as a function of the excitation pulse separation T (cid:24) (cid:16)(cid:4)(cid:2)
and extracting the temporal separation between widely sepa-
ratedminima(cid:3)10,11(cid:4).Anadvantageofthetechniqueusedin (cid:23)(cid:16)(cid:9)(cid:12)(cid:10)(cid:15) (cid:21)(cid:3)(cid:8)(cid:3)(cid:4)
this work is that the periodic signal can be detected with
100% contrast. Although the time scale and precision asso- FIG. 3. TheAI involves off-resonant standing wave excitation
ciated with the experiment should be limited only by the and manipulation of atoms in the ground state. Here, (cid:5) is the
res
transittimeoftheatomsthroughtheregionofinteraction,in atomicresonancefrequencyand(cid:5) isthelaserfrequency.
L
practice it is necessary to eliminate the effects of decoher-
ence due to atomic collisions and background light. Mag- The system is modeled semiclassically as a collection of
netic field gradients also cause amplitude oscillations that two-levelatoms.Foroff-resonantexcitationpulsesshownin
mustbeeliminated(cid:3)12(cid:4).Aninterestingaspectofthisexperi- Fig. 3 the excited state can be adiabatically eliminated. Dur-
mentisthattheDopplerphasesaccumulatedbythemomen- ing the first standing wave excitation pulse which is applied
tum states are canceled at the echo times. As a result the at t=0 the Hamiltonian of the atom-field system is given by
experiment does not rely on velocity selection. The primary (cid:7) (cid:8)
benefit of cooling the sample is to extend the transit time. pˆ2 (cid:2)(cid:1)(cid:7)+i(cid:8)(cid:2) V(cid:1)r(cid:2)
Spontaneous emission during the excitation pulses results H= − . (cid:1)1(cid:2)
2M V(cid:1)r(cid:2) 0
inachangeintheshapeoftheechoenvelopeandinducesan
asymmetry in the periodic T-dependent echo amplitude.The
Here p is the momentum associated with the atom, (cid:7)(cid:5)(cid:5)
changeintheechoamplitudeversusTisalsoassociatedwith L
−(cid:5) is the detuning of the laser from the excited state, (cid:8) is
atemporaloffset(cid:3)10(cid:4).UnderstandingtheimpactofSEplays res
the effective radiative decay rate of the excited state, and
acrucialroleinfittingtheT-dependentsignalandextracting
V(cid:1)r(cid:2) is the spatially periodic atom-field coupling. Because
(cid:5). In this work, we present a calculation of the echo signal
q the laser field creates a standing wave, V(cid:1)r(cid:2) is given by
including the effect of SE and show that this theoretical
(cid:9) (cid:10)
model is effective in describing the echo envelope and
(cid:6)E q·r
T-dependent signal shape. A measurement of the effective V(cid:1)r(cid:2)= 0 cos , (cid:1)2(cid:2)
radiative rate of the sample can be extracted from fits to the 2 2
data. The effective rate shows the predicted dependence on
the detuning of the standing wave pulses. The measured ra- whereE0istheamplitudeoftheelectricfield,(cid:6)isthedipole
diativerateexhibitsacharacteristicdependenceonthedura- moment,andr isthepositionoftheatominthepotential.If
tion of the second standing wave pulse.This rate asymptoti- thepulsesaresufficientlyshort,thedistancetheatomsmove
cally approaches the radiative rate for an isolated atom for duringthepulseissmallcomparedtotheperiodofthestand-
sufficiently long interaction pulses. Using a numerical simu- ing wave potential (cid:4)/2. It is then possible to ignore the ki-
lation involving the dressed state basis, we show that this netic energy term pˆ2 in the Hamiltonian (cid:1)Raman-Nath ap-
2M
effect is related to atomic motion in the periodic optical po- proximation(cid:2) during the excitation pulse. Using this
tential as well as in the spatial profile of the excitation approximation, the expression for the interaction potential
beams.We also present studies of the T-dependent echo am- energy for the ground state becomes
plitude as a function of the strength of the atom-field cou-
pling (cid:1)pulse area(cid:2), spatial profile of excitation beams, and V2(cid:1)x(cid:2) (cid:2)(cid:5)2
U(cid:1)x(cid:2)= (cid:11) 1 cos(cid:1)qx(cid:2), (cid:1)3(cid:2)
momentum imparted to the atoms and compare with (cid:2)(cid:1)(cid:7)+i(cid:8)(cid:2) 8(cid:1)(cid:7)+i(cid:8)(cid:2)
predictions.
Therestofthepaperisorganizedasfollows.InSec.IIwe where x is the position of the atom along the direction of q,
describe a calculation of the echo signal including the effect (cid:5)=(cid:6)E0 is the Rabi frequency, and a constant term has been
of SE during the pulses. Some of the details pertaining to 1 (cid:2)
ignored.
manipulation of Bessel functions used in the calculation are
For an initial atomic plane wave, the wave function is
presented in theAppendix.The experimental details are pre- (cid:12)(cid:9)(cid:1)t=0(cid:2)(cid:13)(cid:10)eik0x, where k is the initial momentum.Applying
sentedinSec.IIIandadiscussionofthedataisgiveninSec. 0
the time evolution operator we obtain
IV. Finally, we compare the data with numerical simulations (cid:7) (cid:8)
(cid:14)
based on dressed states to understand the effective radiative
i t
rate of the system. (cid:12)(cid:9)(cid:1)t(cid:2)(cid:13)=exp − H˜(cid:1)t(cid:1)(cid:2)dt(cid:1) (cid:12)(cid:9)(cid:1)0(cid:2)(cid:13) (cid:1)4(cid:2)
(cid:2)
0
II.THEORY
˜
We first describe the calculation used to model the echo at any time, t, during the excitation pulses. Here H is the
signal presented in Refs. (cid:3)10,14–16(cid:4) and then consider the effective Hamiltonian. For an excitation pulse of duration t
effects of SE and spatial profile. =(cid:11) we find
1
013610-2
INFLUENCEOFSPONTANEOUSEMISSIONONA… PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
(cid:12)(cid:9)(cid:1)(cid:11)(cid:2)(cid:13)=exp(cid:3)i(cid:12) cos(cid:1)qx(cid:2)+ik x(cid:4) (cid:1)5(cid:2) (cid:14)
1 1 0 i(cid:17)J(cid:17)„2u(cid:1)sin(cid:1)(cid:1)/2(cid:2)…= (cid:15) ei(cid:17)(cid:1)/2Jl+(cid:17)(cid:1)u(cid:1)(cid:2)Jl(cid:1)u(cid:1)(cid:2)eil(cid:1) (cid:1)11(cid:2)
where (cid:12)(cid:5)− (cid:5)12 (cid:11) is the area of the first standing wave l=−(cid:14)
1 8(cid:1)(cid:7)+i(cid:8)(cid:2) 1
pulse. For the far-detuned case, (cid:7)(cid:13)(cid:8), we can ignore the so that
effeNcetxotf, t(cid:8)heinJaEcqo.b(cid:1)i3-A(cid:2)nsogetrhaetxp(cid:12)a1n=si−o8n(cid:5)(cid:7)12c(cid:11)a1.n be used to rewrite (cid:9)*(cid:9)=2J1„2(cid:12)1sin(cid:1)(cid:5)qt(cid:2)…cos(cid:1)qx−2(cid:16)(cid:5)0(cid:1)(cid:5)qt(cid:2). (cid:1)12(cid:2)
(cid:12)(cid:9)(cid:1)(cid:11)(cid:2)(cid:13) after the standing wave interaction so that this is the signal that is relevant to Kapitza-Dirac scattering
1
for neutral atoms which was demonstrated in Ref. (cid:3)18(cid:4). The
(cid:9)(cid:1)(cid:11)1(cid:2)= (cid:15)(cid:14) inJn(cid:1)(cid:12)1(cid:2)ei(cid:1)nq+k0(cid:2)x, (cid:1)6(cid:2) tveerlmoccitoynotafinthinega(cid:5)to0(cid:1)mins.tThheeabreocvoeileqpueraitoiodnciasndbueeetoxttrhaectienditbiayl
n=−(cid:14) measuring the amplitude of the density grating as a function
whereJ (cid:1)x(cid:2) isthenthorderBesselfunctionofthefirstkind. of t. However, Eq. (cid:1)12(cid:2) must be integrated over the velocity
n
distribution. The distribution would cause the atoms to
Each Fourier component of index n in the summation repre-
sents a process transferring n(cid:2)q momentum to the atom. dephase on a time scale much smaller than (cid:5)q−1 unless the
sample temperature is ultracold as in a Bose-Einstein con-
Each two-photon process involves absorption of a photon
densate(cid:1)BEC(cid:2)(cid:3)19(cid:4).However,ifasecondpulseisappliedat
from one traveling wave component of the standing wave
t=T the effect of Doppler dephasing can be canceled and an
pulse and stimulated emission in the direction of the other
echo signal can be observed at t=2T. Even if the sample is
travelingwave.Therefore,theFourierseriesrepresentsasu-
perposition of plane waves separated in momentum by (cid:2)q notultracold,itispossibletoobservetheeffectsofrecoilby
with amplitudes weighted by Bessel functions. Equation (cid:1)6(cid:2) measuring the echo amplitude as a function of T. We note
thatforourexperimentalconditions,themostprobablespeed
can be expanded to give
associatedwiththeatomcloudv (cid:6)20v wherev =(cid:2)q/M is
T r r
(cid:12)(cid:9)(cid:1)(cid:11)(cid:2)(cid:13)=J (cid:1)(cid:12)(cid:2)(cid:12)p (cid:13)+iJ (cid:1)(cid:12)(cid:2)(cid:12)p +(cid:2)q(cid:13)+iJ (cid:1)(cid:12)(cid:2)(cid:12)p −(cid:2)q(cid:13) the recoil velocity.
1 0 1 0 1 1 0 1 1 0
After the first standing wave pulse, the system undergoes
−J2(cid:1)(cid:12)1(cid:2)(cid:12)p0+2(cid:2)q(cid:13)−J2(cid:1)(cid:12)1(cid:2)(cid:12)p0−2(cid:2)q(cid:13)+ ¯, (cid:1)7(cid:2) free space evolution according to Eq. (cid:1)8(cid:2).The second stand-
ing wave excitation pulse (cid:1)pulse area (cid:12)(cid:2) affects the atomic
where (cid:12)p (cid:13)(cid:5)eik0x and (cid:12)p +n(cid:2)q(cid:13)(cid:5)ei(cid:1)k0+nq(cid:2)x. 2
0 0 plane waves in the same way as the first excitation pulse
After the standing wave pulse is turned off, the state will
affects the initial plane wave so that
undergo free space evolution according to
(cid:15)
(cid:9)(cid:1)t=T(cid:2)= i(cid:1)n+m(cid:2)J (cid:1)(cid:12)(cid:2)J (cid:1)(cid:12)(cid:2)
p2 (cid:2)2(cid:1)nq+k (cid:2)2 n 1 m 2
H= = 0 . (cid:1)8(cid:2) n,m
2M 2M (cid:15)ei(cid:3)(cid:1)m+n(cid:2)qx−n2(cid:5)qT−nqv0T(cid:4)ei(cid:1)k0x−(cid:5)0(cid:1)T(cid:2), (cid:1)13(cid:2)
The atomic density distribution after the first pulse can then
where v =(cid:2)k /M is the initial velocity of the atomic plane
be calculated as 0 0
wave.
(cid:9)*(cid:9)= (cid:15) i(cid:1)n−n(cid:1)(cid:2)Jn(cid:1)(cid:12)1(cid:2)Jn(cid:1)(cid:1)(cid:12)1(cid:2) funActtioantiemveoltvaefstearsthesecondstandingwavepulse,thewave
n,n(cid:1)
(cid:15)ei(cid:3)(cid:1)n−n(cid:1)(cid:2)qx−(cid:1)n2−n(cid:1)2(cid:2)(cid:5)qt(cid:4)e−2i(cid:1)n−n(cid:1)(cid:2)(cid:16)(cid:5)0(cid:1)(cid:5)qt. (cid:1)9(cid:2) (cid:9)(cid:1)t(cid:2)=(cid:9)(cid:1)T(cid:2)e−i(cid:3)(cid:5)0(cid:1)+(cid:1)m+n(cid:2)qv0+(cid:1)n+m(cid:2)2(cid:5)q(cid:4)t. (cid:1)14(cid:2)
Using Eq. (cid:1)14(cid:2) to find (cid:9)*(cid:9)it can be shown that
To detect the density modulation present in the ground
state after the first standing wave pulse, a traveling wave (cid:9)*(cid:9)= (cid:15) Jn(cid:1)(cid:12)1(cid:2)Jn(cid:1)(cid:1)(cid:12)1(cid:2)Jm(cid:1)(cid:12)2(cid:2)Jm(cid:1)(cid:1)(cid:12)2(cid:2)
readout pulse must be applied. The readout pulse is at the n,m,n(cid:1),m(cid:1)
same frequency as the excitation pulse and is applied along
k . Light is backscattered off the atomic density grating (cid:15)i(cid:1)n+m−n(cid:1)−m(cid:1)(cid:2)ei(cid:1)m+n−n(cid:1)−m(cid:1)(cid:2)qx
2
along k1. This detection scheme ensures that only momen- (cid:15)e−iqv0(cid:3)(cid:1)n+m−n(cid:1)−m(cid:1)(cid:2)t+(cid:1)n−n(cid:1)(cid:2)T(cid:4)
tum states differing by q=2k will contribute to the signal.
The signal is proportional to the amplitude of the spatial (cid:15)e−i(cid:1)n2−n(cid:1)2(cid:2)(cid:5)qTe−i(cid:3)(cid:1)n+m(cid:2)2−(cid:1)n(cid:1)+m(cid:1)(cid:2)2(cid:4)(cid:5)qt. (cid:1)15(cid:2)
harmonicwithperiod(cid:4)/2.Inourcase,thespatialharmonics
are restricted to n−n(cid:1)(cid:5)−(cid:16)=±1. Thus, with a change of The echo technique ensures that only terms independent of
summation indices, we can simplify Eq. (cid:1)9(cid:2) to obtain the initial velocity contribute to the signal. In addition, only
momentum states differing by (cid:2)q will interfere and result in
(cid:15) (cid:15)
(cid:9)*(cid:9)= i−(cid:16) Jn(cid:1)(cid:12)1(cid:2)Jn+(cid:16)(cid:1)(cid:12)1(cid:2) backscattering from the readout pulse. Using these condi-
(cid:16)=±1 n tions, it can be shown that
(cid:16)
(cid:15)ei(cid:3)−(cid:16)qx+(cid:16)(cid:1)2n+(cid:16)(cid:2)(cid:5)qt(cid:4)e2i(cid:16)(cid:5)0(cid:1)(cid:5)qt. (cid:1)10(cid:2) (cid:9)*(cid:9)(cid:1)t=2T(cid:2)=2(cid:1)−1(cid:2)Ncos(cid:3)q(cid:1)x−v0(cid:7)t(cid:2)(cid:4)
(cid:15)J 2(cid:12) sin(cid:1)(cid:5)(cid:7)t(cid:2)
ItispossibletocompressthesumoverninEq.(cid:1)10(cid:2)byusing N„ 1 q …
a Bessel function identity given in Ref. (cid:3)17(cid:4). (cid:15)J 2(cid:12) sin(cid:3)(cid:5)(cid:1)NT+(cid:7)t(cid:2)(cid:4) , (cid:1)16(cid:2)
N+1„ 2 q …
013610-3
BEATTIEetal. PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
where (cid:7)t=t−2T and N=1 for the echo at t=2T. Assuming intensity detection, the integrated signal represents the echo
that the time between standing wave pulses is much greater amplitude. To study the T-dependent behavior of the signal,
than the dephasing time of the echo (cid:1)qv T(cid:13)1(cid:2), we can av- we fit the echo amplitude to (cid:9)*(cid:9)for electric field detection
T
erage over the Maxwell-Boltzmann velocity distribution of and (cid:12)(cid:9)*(cid:9)(cid:12)2 for intensity detection.We therefore use the term
the sample to obtain echoamplitudethroughoutthepapertodescribethestrength
(cid:7) (cid:9) (cid:10) (cid:8)
oftheT-dependentsignalobtainedfromeitherofthesetech-
qv (cid:7)t 2
(cid:9)*(cid:9)(cid:10)exp − T J 2(cid:12) sin(cid:1)(cid:5)(cid:7)t(cid:2) niques.
2 1„ 1 q … We now describe several aspects of the signal shape fol-
lowingamoredetailedderivationthatincludestheeffectsof
(cid:15)J 2(cid:12) sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)(cid:4) . (cid:1)17(cid:2)
2„ 2 q … SE and spatial profile of the excitation beams.
Thisexpressionisperiodicin(cid:7)t andT withafrequency(cid:5).
q
The factor containing the first-order Bessel function in Eq. A.Spontaneousemission
(cid:1)17(cid:2) shows that (cid:5) can be determined by keeping the time
q The derivation presented here is based on Refs.
betweenpulses,T,fixedandobservingtheperiodicsignalas (cid:3)14,15,20(cid:4). Equation (cid:1)18(cid:2) neglects several factors that affect
a function of (cid:7)t within the echo envelope if the sample is
thesignalshapesuchasSEanditisinadequateforfittingthe
sufficiently cold. The duration of the echo envelope in the echo amplitude to obtain a precision measurement of (cid:5).
vicinity of t=2T is inversely proportional to the most prob- Equation (cid:1)18(cid:2) was derived as the expression for the echqo
able speed of velocity distribution along the direction of the signalforthecase(cid:7)(cid:13)(cid:8).Thereforetheeffectofspontaneous
excitation pulses, as shown in Fig. 2. There will only be an emission is ignored in Eq. (cid:1)3(cid:2). In general, the potential en-
echo signal over an interval (cid:7)t in which the atoms move a
ergy is complex and the pulse area is given by
distance of the order of the grating spacing (cid:3)(cid:7)t(cid:18)(cid:1)qv (cid:2)−1(cid:4).
T
For the case where (cid:7)t(cid:19)2T, Eq. (cid:1)17(cid:2) can be written in a −(cid:5)2(cid:11)
(cid:12) = 1 =u(cid:1)(cid:11)(cid:2)ei(cid:20) (cid:1)19(cid:2)
simplerformbyassumingthattheinteractionpulseareasare 1 8(cid:1)(cid:7)+i(cid:8)(cid:2)
small (cid:1)(cid:12)(cid:6)(cid:12)(cid:6)1(cid:2) (cid:3)10(cid:4) so that
1 2 (cid:7) (cid:9) (cid:10) (cid:8) where
qv (cid:7)t 2
(cid:9)*(cid:9)(cid:6)(cid:1)(cid:5)q(cid:7)t(cid:2)exp − 2T J2„2(cid:12)2sin(cid:1)(cid:5)qT(cid:2)…. u(cid:1)(cid:11)(cid:2)= (cid:16)−(cid:5)12(cid:11) (cid:1)20(cid:2)
(cid:1)18(cid:2) 8 (cid:7)2+(cid:8)2
Foralasercooledsamplewithatemperatureof(cid:6)50 (cid:6)K, and (cid:9) (cid:10)
(cid:5) can be measured precisely by measuring the echo ampli- (cid:8)
q
tude as a function of the time between excitation pulses, T. (cid:20)=tan−1 − . (cid:1)21(cid:2)
(cid:7)
Thedetectiontechniquesusedinthemeasurementsareeither
sensitive to the electric field amplitude of the backscattered The definition of (cid:12) in Eq. (cid:1)19(cid:2) is consistent with the defi-
1
light or the associated intensity. For the case of electric field nition of (cid:12) following Eq. (cid:1)5(cid:2). We note that (cid:20)has a similar
1
detection, the echo envelope is shown in Fig. 2. For both form to the phase shift in the emitted radiation due to the
electric field detection and intensity detection, the echo en- damping force for the case of a driven-damped harmonic
velope is recorded with a detection system with a suitably oscillator.Theeffectof(cid:20)istocauseadelayintheformation
high bandwidth. of the grating. As shown in this treatment, (cid:20)influences the
To obtain the echo amplitude we integrate the square of shapeoftheechoenvelopeandtheT-dependentechoampli-
the echo envelope over (cid:7)t for a fixed value of T. The echo tude.UsingEqs.(cid:1)19(cid:2)–(cid:1)21(cid:2)wecanmodifytheexpressionfor
envelopeisintegratedoverthedurationofthesignal(cid:1)several atomic density (cid:9)*(cid:9)following the same steps outlined in the
(cid:6)s(cid:2). For electric field detection, we take the positive square preceding section based on Refs. (cid:3)14,15,20(cid:4). Defining (cid:16)=n
rootoftheintegratedsignaltoobtaintheechoamplitude.For +m−n(cid:1)−m(cid:1) we obtain
(cid:15)
(cid:9)*(cid:9)= i(cid:16)Jn„u(cid:1)(cid:11)1(cid:2)ei(cid:20)…Jn+(cid:16)N„u(cid:1)(cid:11)1(cid:2)e−i(cid:20)…Jm„u(cid:1)(cid:11)2(cid:2)ei(cid:20)…Jm−(cid:16)(cid:1)N+1(cid:2)„u(cid:1)(cid:11)2(cid:2)e−i(cid:20)…ei(cid:16)qxei(cid:16)N(cid:1)2n+(cid:16)N(cid:2)(cid:5)qTe−i(cid:16)qv0(cid:7)te−i(cid:16)(cid:3)2(cid:1)n+m(cid:2)−(cid:16)(cid:4)(cid:5)qT. (cid:1)22(cid:2)
m,n,(cid:16)
Here, (cid:11) represents the duration of the second standing wave pulse. In order to simplify Eq. (cid:1)22(cid:2) we need an identity similar
2
toEq.(cid:1)11(cid:2)thatallowscomplexarguments.TheAppendixdescribesthestepsrequiredtoderivethisidentitywhichiscontained
in Eq. (cid:1)A13(cid:2). Using Eq. (cid:1)A13(cid:2), we obtain an expression for the atomic density in the vicinity of t=2T which is given by
(cid:9) (cid:10) (cid:9) (cid:10)
(cid:15)(cid:14) sin(cid:1)(cid:16)(cid:5)(cid:7)t+(cid:20)(cid:2) (cid:16)N/2 sin(cid:3)(cid:16)(cid:5)(cid:1)NT+(cid:7)t(cid:2)+(cid:20)(cid:4) −(cid:16)(cid:1)N+1(cid:2)/2
(cid:9)*(cid:9)= ei(cid:16)qxe−i(cid:16)qv0(cid:7)t q q
sin(cid:1)(cid:16)(cid:5)(cid:7)t−(cid:20)(cid:2) sin(cid:3)(cid:16)(cid:5)(cid:1)NT+(cid:7)t(cid:2)−(cid:20)(cid:4)
(cid:16)=−(cid:14) q q
(cid:16) (cid:16)
(cid:15)J(cid:16)N„2u(cid:1)(cid:11)1(cid:2) sin(cid:1)(cid:16)(cid:5)q(cid:7)t−(cid:20)(cid:2)sin(cid:1)(cid:16)(cid:5)q(cid:7)t+(cid:20)(cid:2)…J−(cid:16)(cid:1)N+1(cid:2)„2u(cid:1)(cid:11)2(cid:2) sin(cid:3)(cid:16)(cid:5)q(cid:1)NT+(cid:7)t(cid:2)−(cid:20)(cid:4)sin(cid:3)(cid:16)(cid:5)q(cid:1)NT+(cid:7)t(cid:2)+(cid:20)(cid:4)…. (cid:1)23(cid:2)
Becauseourdetectionschemeisonlysensitivetointerferencebymomentumstatesthatdifferby(cid:2)q (cid:1)(cid:16)=±1(cid:2) andweobserve
013610-4
INFLUENCEOFSPONTANEOUSEMISSIONONA… PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
the (cid:4)/2 spatial harmonic at t=2T (cid:1)N=1(cid:2), the infinite sum is truncated and Eq. (cid:1)23(cid:2) can be written as
(cid:9) (cid:10) (cid:9) (cid:10)
sin(cid:1)(cid:5)(cid:7)t+(cid:20)(cid:2) 1/2 sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)−(cid:20)(cid:4)
(cid:9)*(cid:9)=cos(cid:3)q(cid:1)x−v (cid:7)t(cid:2)(cid:4) q q
0 sin(cid:1)(cid:5)(cid:7)t−(cid:20)(cid:2) sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)+(cid:20)(cid:4)
q q
(cid:16) (cid:16)
(cid:15)J 2u(cid:1)(cid:11)(cid:2) sin(cid:1)(cid:5)(cid:7)t+(cid:20)(cid:2)sin(cid:1)(cid:5)(cid:7)t−(cid:20)(cid:2) J 2u(cid:1)(cid:11)(cid:2) sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)+(cid:20)(cid:4)sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)−(cid:20)(cid:4) . (cid:1)24(cid:2)
1„ 1 q q … 2„ 2 q q …
Integrating this expression over the Maxwell-Boltzmann distribution to account for all velocity classes it can be shown that
(cid:7) (cid:9) (cid:10) (cid:8)(cid:9) (cid:10) (cid:9) (cid:10)
qv (cid:7)t 2 sin(cid:1)(cid:5)(cid:7)t+(cid:20)(cid:2) 1/2 sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)−(cid:20)(cid:4)
(cid:9)*(cid:9) (cid:10)exp − T q q
total 2 sin(cid:1)(cid:5)(cid:7)t−(cid:20)(cid:2) sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)+(cid:20)(cid:4)
q q
(cid:16) (cid:16)
(cid:15)J 2u(cid:1)(cid:11)(cid:2) sin(cid:1)(cid:5)(cid:7)t+(cid:20)(cid:2)sin(cid:1)(cid:5)(cid:7)t−(cid:20)(cid:2) J 2u(cid:1)(cid:11)(cid:2) sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)+(cid:20)(cid:4)sin(cid:3)(cid:5)(cid:1)T+(cid:7)t(cid:2)−(cid:20)(cid:4) . (cid:1)25(cid:2)
1„ 1 q q … 2„ 2 q q …
This expression is equivalent to Eq. (cid:1)17(cid:2) for the case where Fig. 4 as a dotted line. Equation (cid:1)17(cid:2) also shows that the
(cid:8)→0.We will now discuss some qualitative differences be- relative amplitudes of the lobes will change in a more com-
tweenthepredictionsofEqs.(cid:1)17(cid:2)and(cid:1)25(cid:2).Wewillseparate plicated cyclical manner if the time between pulses, T, is
thediscussionsintoadescriptionoftheechoenvelopeanda varied. With pulse area and pulse separation fixed, Eq. (cid:1)25(cid:2)
descriptionoftheT-dependentsignalthathasaperiodT . predicts that the echo envelope will have an asymmetric
recoil
Equation (cid:1)18(cid:2) predicts a symmetric echo envelope if (cid:7)t shapeduetoSE,asshownbythedashedlineinFig.4.Other
(cid:19)T and (cid:12)(cid:6)(cid:12)(cid:6)1. For large interaction pulse areas or factors affecting the echo envelope include effects such as
recoil 1 2
ultracold samples Eq. (cid:1)17(cid:2) rather than Eq. (cid:1)18(cid:2) is valid and gravity that affect both arms of the interferometer are dis-
predicts an asymmetric echo envelope. The solid curve in cussed in Ref. (cid:3)12(cid:4). SE also has the effect of delaying the
Fig. 4 shows the symmetric echo envelope predicted by Eq. time at which the signal zero occurs in the vicinity of t=2T.
(cid:1)17(cid:2) if (cid:7)(cid:13)(cid:5). When the first standing wave pulse area in- A comparison of the echo amplitude predicted by Eqs.
1
creases, the echo envelope remains symmetric but becomes (cid:1)18(cid:2) and (cid:1)25(cid:2) is shown in Fig. 5. In the presence of SE the
narrower. This is presumably due to the broadening of the signalamplitudeispredictedtohaveapronouncedasymme-
velocity distribution of the atoms caused by the standing try with respect to the zeros of the function.The zeros sepa-
wave interaction. As the second pulse area increases, the ratedbyT areshowninFig.5.Thiscanattributedtothe
recoil
relative amplitude of the first lobe of the echo envelope be- nonsinusoidalnatureoftheinteractionpotentialdescribedby
comes larger and the amplitudes of the two lobes show a Eq.(cid:1)3(cid:2).Toextractaprecisionmeasurementof(cid:5) itiscrucial
q
cyclical dependence on pulse area. A representation of an to fit the data using an expression that accounts for these
asymmetric shape due to a change in pulse area is shown in asymmetric features (cid:3)which are modeled by Eq. (cid:1)25(cid:2)(cid:4). This
equation also predicts a negative temporal offset in the echo
amplitude due to SE. The temporal offset can be (cid:6)1 (cid:6)s for
typical experimental conditions. Therefore, the delay in the
e
p
o
l
e
v
n
E
o
h
c
E
T
recoil
FIG. 4. Echo envelope: Solid curve shows echo envelope pre-
dicted by Eq. (cid:1)17(cid:2) for T=1ms, (cid:12)=2.5, and (cid:12)=2.6. The dotted
1 2
line shows an asymmetric shape due to the variation in pulse area
for T=1ms, (cid:12)=2.5, and (cid:12)=5.The dashed line shows an asym- FIG. 5. Echo amplitude vs T with and without spontaneous
1 2
metric shape due to SE modeled by Eq. (cid:1)25(cid:2) for T=1ms, u =2.5, emission: Solid line shows echo amplitude vs T based on Eq. (cid:1)18(cid:2)
1
u =2.6, and (cid:20)=−0.02. The dashed line also shows a delay in the where (cid:5)=97000s−1, and (cid:12)=6.The dashed line shows the echo
2 q 2
position of the signal zero in the vicinity of (cid:7)t=0.All curves are amplitude vs T for Eq. (cid:1)25(cid:2) where (cid:5)=97000s−1, u =6, and (cid:20)=
q 2
calculated using a temperature of 100(cid:6)K and assuming that the −0.03.The dashed line shows an asymmetry in the periodic signal
atomicspeciesis 85Rb. inthepresenceofSE,aswellasatemporalshift.
013610-5
BEATTIEetal. PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
formation of the grating due to SE effectively decreases the
values of T at which the zeros occur. Although this effect
does not change the period of the signal, (cid:5) is typically
q
measured by fitting to two widely separated periods (cid:3)11(cid:4). If
the expanding atomic cloud samples different parts of the
standing wave potential or if (cid:7) varies (cid:1)due to the Doppler
shifts associated with the falling atomic cloud(cid:2) when T is
varied, (cid:20)will vary for the widely separate periods resulting
T
in a systematic effect on the measurement of (cid:5). Both the recoil
q
asymmetry and the temporal offset are shown in Fig. 5.
B.Spatialprofile
The expression given in Eq. (cid:1)25(cid:2) has to be further modi-
fied to account for the spatial profile of the interferometry
beams. The derivation leading to Eq. (cid:1)25(cid:2) assumed that the FIG. 6. Echo amplitude vs T showing the effect of spatial pro-
electricfieldwasaplanewavewithuniformamplitude.Due file: The dotted and dashed lines show the echo amplitude vs T
to the Gaussian profile of theAI beams, atoms experience a given by Eq. (cid:1)25(cid:2) with u =6 and u =2.85, respectively. The solid
2 2
spatially varying Rabi frequency and, consequently, sample curve shows the echo amplitude vs T given by Eq. (cid:1)26(cid:2). It can be
different pulse areas. Equation (cid:1)25(cid:2) predicts that increasing seen that an average of signals with a range of pulse areas will
the pulse area results in multiple minima per recoil period resultinasignalshapethatcanbedescribedbyEq.(cid:1)26(cid:2).
andtheechoamplitudevariesmorerapidlyinthevicinityof
(cid:6)140 MHz above resonance.Adual-passAOM (cid:1)AOM1(cid:2) is
thezero.Thiscanbeattributedtotheinterferenceofhigher-
used to frequency shift and amplitude modulate the trapping
order momentum states produced by the first standing wave
laserbeams.TheundiffractedlaserbeamfromAOM1issent
pulse. However, the signal shape between adjacent zeros is
intoanotherdual-passAOM(cid:1)AOM2(cid:2)operatingat(cid:6)80 MHz
observed to be smoothed out. This effect is attributed to the
to derive a laser beam at (cid:6)300 MHz above resonance. This
spatial profile.
beam is split and sent through two AOMS (cid:1)AOM3 and
The signal shape can be modeled by integrating the
Bessel functions in Eq. (cid:1)25(cid:2) over a range of Rabi frequen- AOM4(cid:2) operating at (cid:6)250 MHz to derive excitation pulses
used for atom interferometry that are 50–100 MHz above
cies. This integral results in a generalized hypergeometric
resonance. We load approximately 108 atoms in a magneto-
function. Although this model resulted in signal shapes that
opticaltrap(cid:1)MOT(cid:2)onatimescaleof(cid:6)100 msusingAOM1
are qualitatively in agreement with the observed signal, we
totunethetrappingbeamsto(cid:6)2(cid:8) belowresonance,where
find that the hypergeometric function is not suitable as a fit N
(cid:8) =(cid:1)2(cid:3)(cid:11)(cid:2)−1=6.07 MHz is the natural linewidth, and the ra-
function. However, the signal shape could be fit more accu- N
diativedecaytime,(cid:11)=26.20 ns(cid:3)21,22(cid:4).Afterturningoffthe
rately using the function
(cid:17) (cid:17) gradient coils in (cid:6)500 (cid:6)s, AOM1 is used to shift the trap-
S(cid:1)T(cid:2)=AJ2(cid:3)b(cid:1)1−ed(cid:16)sin(cid:1)(cid:5)qT−(cid:20)(cid:2)sin(cid:1)(cid:5)qT+(cid:20)(cid:2)(cid:2)(cid:4) ssiinn(cid:1)(cid:1)(cid:5)(cid:5)qTT+−(cid:20)(cid:20)(cid:2)(cid:2) , apinmgoblaesasmessftoor(cid:6)(cid:6)55(cid:8)Nmbs.elTohwertersaopnpainngcebaenadmcsoaorleththeeantotumrsneind
q off for (cid:6)25 ms during which time AOM2, AOM3, and
(cid:1)26(cid:2)
AOM4areturnedontogeneratetravelingwavecomponents
whereAisanoverallscalefactorandtheparametersbandd of the standing wave pulses as well as the traveling wave
are related to the pulse area. readout pulse. The excitation pulses have approximately the
Simulations of the signal shape using Eq. (cid:1)26(cid:2) show that same diameter as the initial size of the cloud (cid:1)(cid:6)4 mm(cid:2).The
additional zero crossings are averaged out to give a periodic temperature of the sample is inferred by photographing the
signal that has only one local minimum per recoil period as ballistic expansion of the cloud using a charge-coupled de-
shown in Fig. 6. This figure shows that the solid line based vice (cid:1)CCD(cid:2) camera and is typically (cid:6)50 (cid:6)K (cid:3)23(cid:4).The echo
on Eq. (cid:1)26(cid:2) represents the effect of averaging the echo am- signal is detected by backscattering the readout pulse from
plitude over a range of pulse areas. the sample. In this work, we have used two separate tech-
niques represented in Fig. 7 to detect the echo. Heterodyne
detection shown in Fig. 7(cid:1)a(cid:2) requires an optical local oscil-
III.EXPERIMENT
lator (cid:1)LO(cid:2) which is derived by using the undiffracted beam
The light used for trapping and interferometry is derived from AOM3. The LO is spatially separated from the dif-
from a singleTi:Sapphire ring laser with an output power of fracted beam by (cid:6)2.5 cm to minimize decoherence due to
(cid:6)1 W.Therepumplaserisderivedfromagratingstabilized scattered light. PulsingAOM2 ensures that the LO is turned
diode laser.Asmall portion of the Ti:Sapphire laser light is ononlyforthedurationoftheexcitationandreadoutpulses,
sent through a saturation absorption spectrometer that in- thereby minimizing decoherence due to background light.
cludesadualpassacousto-opticmodulator(cid:1)AOM(cid:2)operating Pulsing this AOM also ensures that standing wave pulses
at (cid:6)70 MHz and serving as a tuning element. The laser is have an on and/or off contrast of greater than 106:1. The
locked to the 5S1/2 F=3 to 5P3/2 F=4 trapping transition in backscattered signal is combined with the LO on a balanced
85Rb so that the laser beam used in the experiment is heterodyne detector that detects the presence of the echo in
013610-6
INFLUENCEOFSPONTANEOUSEMISSIONONA… PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
5
(cid:2)
s
t
i 4
(cid:1)(cid:2)(cid:3)(cid:4) un
(cid:13)(cid:9)(cid:6)(cid:8)(cid:13)(cid:9)(cid:2)(cid:6)(cid:7)(cid:13)(cid:13)(cid:8)(cid:3)(cid:9)(cid:16) (cid:2)(cid:5)(cid:4) b.
r 3
a
(cid:1)
(cid:19)(cid:16)(cid:8)(cid:11)
e
d
(cid:2)(cid:5)(cid:4) tu 2
i
l
(cid:29)(cid:4)(cid:8) (cid:25)(cid:26)(cid:27)(cid:28) mp
(cid:21)(cid:11)(cid:13)(cid:7)(cid:3)(cid:3)(cid:4)(cid:16) a 1
o
h
(cid:29)(cid:4)(cid:8) c
e
(cid:21)(cid:11)(cid:13)(cid:7)(cid:3)(cid:3)(cid:4)(cid:16) 0
0 100 200 300 400
(cid:29)(cid:8)(cid:13)(cid:8)(cid:10)(cid:6)(cid:4)(cid:15) (a) T (cid:1)Μs(cid:2)
(cid:30)(cid:4)(cid:3)(cid:4)(cid:16)(cid:9)(cid:15)(cid:31)(cid:10)(cid:4)
(cid:15)(cid:4)(cid:3)(cid:4)(cid:6)(cid:3)(cid:7)(cid:9)(cid:10)
(a)
(cid:2) 1.2
s
t
i
n 1
u
.
b
r 0.8
(cid:2)(cid:30)(cid:12)(cid:3)(cid:3)(cid:4)(cid:16) a
(cid:1)
de 0.6
u
t
(cid:19)(cid:16)(cid:8)(cid:11) pli 0.4
(cid:2)(cid:5)(cid:4) m
a
(cid:29)(cid:4)(cid:8) ho 0.2
(cid:21)(cid:11)(cid:13)(cid:7)(cid:3)(cid:3)(cid:4)(cid:16) !(cid:27)(cid:19) ec
0
0 100 200 300 400
(cid:25)(cid:26)(cid:27)(cid:28) (b) T (cid:1)Μs(cid:2)
FIG. 8. Echo amplitude vs T: Illustrates the difference in (cid:5)
q
between(cid:1)a(cid:2)counterpropagatingexcitationbeams(cid:1)(cid:21)(cid:18)1mrad(cid:2) and
(b) (cid:1)b(cid:2)excitationbeamsatanangleof(cid:21)=(cid:3)/2.ThedataarefitbyEq.
(cid:1)18(cid:2). The fits give (cid:5)=9.7(cid:15)104s−1 and (cid:12)=2.1 for (cid:1)a(cid:2) and (cid:5)
q 2 q
FIG.7. Experimentalsetupforthecasesofheterodynedetection =4.9(cid:15)104s−1and(cid:12)=2.2for(cid:1)b(cid:2).Theuncertaintyin(cid:5) extracted
2 q
in(cid:1)a(cid:2)andphotomultipliertube(cid:1)PMT(cid:2)detectionin(cid:1)b(cid:2). from the fits is (cid:6)1/103 and the signal decay time is much smaller
thanthetransittimeduetocollisions,scatteredlight,andmagnetic
the form of a beat note at 250 MHz. The two outputs of the
fieldgradients.
detector are mixed down to dc using the rf oscillator used to
driveAOM3 andAOM4. The rf used to produce one of the
envelope is detected using a gated photomultiplier tube
dccomponentsisphaseshiftedby(cid:3)/2 withrespecttotherf
(cid:1)PMT(cid:2).ThePMThasarisetimeof(cid:6)10 nsandthegatecan
used to derive the other dc component. The two dc compo-
be fully opened on a time scale of 100 ns. Since the shutter
nents are filtered using a 20 MHz low-pass filter and repre-
hasajitterof(cid:6)200 (cid:6)s,thesmallestpulseseparations,T,for
sent the in-phase and quadrature components of the back-
which the echo can be recorded is (cid:6)1 ms. The echo enve-
scatteredelectricfield.Thisbackscatteredelectricfieldisthe
lope, which resembles the square of the signal shape shown
characteristic echo envelope shown in Fig. 2. These signals
in Fig. 2 is recorded using a 20 MHz low-pass filter. The
are squared and integrated over the duration of the signal (cid:1)a
echo envelope is integrated over the duration of the signal
few (cid:6)s(cid:2). The positive square root of the sum of the squared
(cid:1)few (cid:6)s(cid:2) to obtain the echo amplitude.
signals represents the echo amplitude. AOM2, AOM3, and
The peak intensities of the standing wave beams are I
AOM4 are controlled by digital delay generators. The time
(cid:6)10I where I =7.56 mWcm2 is the saturation intensity
base of these generators is referenced to a 10 MHz signal sat sat
for equally populated magnetic sublevels of the F=385Rb
from a Rb atomic clock with anAllan variance of 2(cid:15)10−12
ground state. The durations of the first and second standing
at100 seconds.The250 MHzoscillatorusedtodriveAOM3
wave pulses are 500–800 ns and 30–200 ns, respectively.
andAOM4 is also phase locked to the Rb clock.
Theechosignalisdetectedusingareadoutpulsethathasthe
An alternate detection scheme for intensity detection is
same detuning as the excitation pulses.
shown in Fig. 7(cid:1)b(cid:2). This scheme uses only AOM2 and
AOM3aswellasaretroreflectingmirrortoproducestanding
IV.RESULTS
wave pulses. A shutter with a closing time of (cid:6)600 (cid:6)s for
the 4 mm excitation beams is used to block the retroreflec- The simplified expression for the echo amplitude in the
tion at the time of the readout pulse. In this case, the echo absenceofSEgivenbyEq.(cid:1)18(cid:2)showsthattheperiodofthe
013610-7
BEATTIEetal. PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
(cid:3)(cid:1)(cid:2)1Recoilfrequencys 9999966667999902468000000 0 0.01 0.02 0.03 0.04 0.05 0.06 (cid:1)(cid:2)EchoEnvelopearb.units000001......024680 (cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)(cid:2)(cid:1)(cid:3)
Γ (cid:1)rad(cid:2) (cid:1)1 0 1 2
(cid:2)t(cid:1)Μs(cid:2)
FIG.9. Showsafitbydatameasuring(cid:5) asafunctionof(cid:21).The
q
fit function is bcos2(cid:1)a(cid:21)/2(cid:2) where a=0.991±0.016 and b FIG. 10. Background subtracted traces of the echo envelope
=97004.4±0.6s−1. obtainedbybackscatteringthereadoutpulsefromtheatomiccloud.
Thetracesrepresentanaverageof32repetitions.Thetypicalback-
signaldependsonq.Wehavevariedqbychangingtheangle ground is typically 1% of the amplitude of the echo envelope.
(cid:22)between the traveling wave components of the excitation Squares represent a symmetric echo envelope recorded with (cid:7)
pulses.When(cid:22)issetto180°weobservetheperiodicsignal =55MHz and (cid:11)2=155ns. Fit to Eq. (cid:1)17(cid:2) (cid:1)solid line(cid:2) gives a tem-
shown in Fig. 8(cid:1)a(cid:2). When (cid:22)=90° the period of the signal is peratureof(cid:6)80(cid:6)K,(cid:12)1=1.4,and(cid:12)2=2.8.Circlesrepresentasym-
doubled, as expected, as shown in Fig. 8(cid:1)b(cid:2). In both cases, metric echo envelope obtained by increasing the second pulse du-
the fit by the data was based on Eq. (cid:1)18(cid:2) and the point spac- rationto(cid:11)2=300ns.FittoEq.(cid:1)25(cid:2)(cid:1)solidline(cid:2)givestemperatureof
90(cid:6)K,u =0.9,and(cid:20)=−.025.Trianglesrepresentasymmetricecho
ing is adequate to resolve the difference in the period. The 1
envelopeobtainedwith(cid:7)=25MHzand(cid:11)=155ns.FittoEq.(cid:1)25(cid:2)
fits also included a phenomenological decay term to account 2
(cid:1)solid line(cid:2) gives temperature of 60(cid:6)K, u =4, and (cid:20)=−0.03. The
fortheexponentialdecayofthesignalamplitude.Thedecay central minima at (cid:7)t=0 is nonzero due to1a limitation of the PMT
in Fig. 8 was primarily due to background light and colli- detectionsystem.Thesignallevelsat(cid:7)t=±2(cid:6)srepresentthetrue
sions with rubidium atoms at room temperature. For precise zero of the signal. For heterodyne detection, (cid:1)see data overlaid in
measurements of (cid:5)r we rely on Eq. (cid:1)26(cid:2), which includes the Fig. 2(cid:2) the signal at (cid:7)t=0 has been verified to be zero within ex-
effects of both SE and spatial profile, and we take data with perimentalerror.
a point spacing of (cid:6)250 ns. Figure 9 shows the dependence
of(cid:5)ron(cid:22)forthecasewhentheangleisvariedoverasmall 12. The echo amplitude is recorded over two widely sepa-
range with respect to (cid:22)=180°. Both Figs. 8 and 9 show that rated periods. In this case a multiparameter fit based on Eq.
the recoil frequency has the predicted dependence on angle (cid:1)26(cid:2) gives a fit error for (cid:5) of (cid:6)3 parts per 106 (cid:1)ppm(cid:2). The
givenby(cid:5)q=(cid:2)q2/2M andq=2ksin(cid:22)/2.Forprecisionmea- fit also includes a Gaussiaqn decay parameter to account for
surements of (cid:5)r (cid:3)11(cid:4), which are carried out at (cid:22)(cid:6)180°, the the signal decay. The other fit parameters (cid:1)A,b,d,(cid:20)(cid:2) are de-
dataarecorrectedfortheangleusingthefitshowninFig.9, termined to a precision of (cid:6)10%. Similar fit errors for A, b,
which is based on the predicted expression (cid:5)r(cid:1)(cid:21)(cid:2) d, and (cid:20)are obtained for all fits based on Eq. (cid:1)26(cid:2) (cid:1)Figs.
=(cid:5)r(cid:1)180°(cid:2)cos2(cid:1)(cid:21)/2(cid:2), where (cid:21)=180°−(cid:22). 11–13and15(cid:2).WiththeexceptionofFig.12(cid:1)inwhichthefit
Figure10showsatestofthepredictionsofEqs.(cid:1)17(cid:2)and
(cid:1)25(cid:2) for the echo envelope. For large detunings the data are
accuratelymodeledbyEq.(cid:1)17(cid:2)andsymmetricenvelopesare 0.6 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)
obtained.The pulse area is varied by increasing the duration (cid:2) (cid:2)
of the second standing wave pulse and the effect of sponta- (cid:2)nits0.5 (cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)
neous emission is varied by changing the detuning. Both u (cid:2)
cttesruqifarfducteWeealc.ertetessIhnsenacnoFaaeurdwifegsft.eerufic1isaatt1essnyutgothmshlfieeenmsSgdtEeaahtrEteraaeioqncrrfi.deestp(cid:1)tisi1gurcpe7nsaasi(cid:2)altneliganatrsnltehEdapaaqtrpmsto.ehifin(cid:1)ese2lg.ne5ltdDe(cid:2)oa.iantrntaeactShroreeeeicplp.errpeceIesIhsreeoitnonotadteem.iddlTlpubbhlsiyye-- (cid:1)EchoAmplitudearb.0000....1234 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)
(cid:1)p2o5in(cid:2),tasnedpa(cid:1)r2a6ti(cid:2)o.nItisis2c5l0eanrsthanatdtfihetseaxrperebsassieodn obnaseEdqso.n(cid:1)1E8q(cid:2)., 0.0 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)
830 840 850 860 870
(cid:1)26(cid:2)thatincludestheeffectsofbothSEandspatialprofileis T(cid:1)Μs(cid:2)
necessaryforobtaininganaccuratefittotheamplitudeofthe
periodic signal. FIG. 11. Echo amplitude vs T. The data for (cid:7)=50MHz (cid:1)solid
To illustrate the importance of Eq. (cid:1)26(cid:2) for a precision circles(cid:2) are fit with Eq. (cid:1)18(cid:2) (cid:1)dotted line(cid:2), Eq. (cid:1)25(cid:2) (cid:1)dashed line(cid:2),
measurement, we show a typical measurement of (cid:5) in Fig. andEq.(cid:1)26(cid:2)(cid:1)solidline(cid:2).
q
013610-8
INFLUENCEOFSPONTANEOUSEMISSIONONA… PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
0.6 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) 12
(cid:2) (cid:2)
(cid:2)units0.5 (cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:2)units10
(cid:1)EchoAmplitudearb.0000....1234 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:1)EchoAmplitudearb. 2468
(cid:2) (cid:2)
0.0 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) 0
830 840 850 860 870 850 860 870 880 890 900 910
(a) T(cid:1)Μs(cid:2) (a) T(cid:1)Μs(cid:2)
(cid:2)(cid:2)(cid:2)(cid:2) 12
0.25 (cid:2)(cid:2)
(cid:2) (cid:2)
(cid:2) (cid:2)
(cid:1)(cid:2)EchoAmplitudearb.units00000.....0011205050 (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2) (cid:1)(cid:2)EchoAmplitudearb.units102468
0
8930 8940 8950 8960 8970
850 860 870 880 890 900 910
(b) T(cid:1)Μs(cid:2)
(b) T(cid:1)Μs(cid:2)
FIG. 12. A typical recoil measurement with (cid:7)=50MHz. The
measurementiscarriedoutbyfittingthedatabyEq.(cid:1)26(cid:2)andcon-
sistsofonerecoilperiodrecordedatT(cid:6)900(cid:6)sandasecondrecoil 10
periodrecordedatT(cid:6)9000(cid:6)s.Thefitgives(cid:5)=97008.5(cid:1)4(cid:2)s−1.
error for (cid:5) is (cid:6)3 ppm(cid:2), the fit error foqr (cid:5) is typically (cid:2)units 8
(cid:6)pa1re/d10t3o. Tthhqee tdimatae isncaFleig.in12Fihgasv.e8ableocnagusdeectaqhyeteimffeecctsomof- (cid:1)udearb. 6
background collisions, stray light, and magnetic field gradi- plit
ents have been reduced. The importance of including the Am 4
o
h
effects of SE and spatial profile on a precision measurement Ec
of(cid:5) arequitedramatic.Forexample,(cid:5) canbedetermined 2
q q
toaprecisionof(cid:6)1/1000ifthesignaldecaytimeis(cid:6)1 ms
(cid:3)10,13(cid:4).Although the signal decay time in Fig. 12 has been 0
850 860 870 880 890 900 910
increased by only a factor of (cid:6)20 the precision in (cid:5)q has (c) T(cid:1)Μs(cid:2)
improvedbyafactorof(cid:6)1000.Sincetheprecisionincreases
linearly with T, it can be seen that the improvements to the FIG. 13. The effect of varying the pulse area of the second
theoretical expressions used in the fits have contributed as excitationpulseonthesignalshapewith(cid:7)=70MHz.Thefitfunc-
much as a factor of (cid:6)50 to the improvement in precision. tionsarebasedonEq.(cid:1)26(cid:2)andthepulsedurationsare(cid:1)a(cid:2)40ns,(cid:1)b(cid:2)
To understand the predictions for the effect of the atom- 60ns,and(cid:1)c(cid:2)100ns.
field coupling on the echo amplitude, we vary the pulse area
(cid:12) by adjusting the duration of the second standing wave decreasing the relative uncertainty in determining the posi-
2
pulseasshowninFig.13.Thedatawerefitusingexpression tions of the zeros.
(cid:1)26(cid:2). As expected, the signal shape shows a sinusoidal de- Figure 14 shows the dependence of the effective pulse
pendenceforsmallpulsedurations(cid:1)(cid:6)40 ns(cid:2)andsharplyde- area (cid:3)given by the product of the fit parameters b and d in
finedminimaforlongerpulsedurations(cid:1)(cid:6)500 ns(cid:2).Thenar- Eq.(cid:1)26(cid:2)(cid:4)on(cid:11).ForthesedatatheRaman-Nathcriterionwas
2
rowing of the signal shape in the vicinity of the zeroes is satisfied for pulse widths up to (cid:6)3 (cid:6)s. We note that in Eq.
attributedtointerferenceofhigher-ordermomentumcompo- (cid:1)18(cid:2) the pulse area of the second standing wave pulse is
nents that are rephased by the second standing wave pulse. defined as (cid:12)=(cid:1)(cid:5)2/8(cid:7)(cid:2)(cid:11) where (cid:11) is the pulse duration.
2 1 2 2
Thus, controlling the pulse width plays an important role in This equation predicts that the pulse area should increase
013610-9
BEATTIEetal. PHYSICALREVIEWA77,013610(cid:1)2008(cid:2)
5
2.5
(cid:2)Units4 (cid:2)b.units2.0
(cid:1)nd2PulseAreaArb.23 (cid:1)EchoAmplitudear011...505
1
0.0
0 850 860 870 880 890 900 910
0 100 200 300 400 500 600 700
(a) T(cid:1)Μs(cid:2)
Τ2(cid:1)ns(cid:2)
FIG.14. Themeasuredpulseareaasafunctionofsecondexci- 3.0
tationpulseduration.
2.5
linearly with pulse duration. Therefore the slope of pulse (cid:2)nits
tairoena.vHso(cid:11)w2erveeprr,eFseign.ts1t4heshsotrwensgtthhatofthteheefafteocmtiv-fieelpdulisnetearraeca- (cid:1)arb.u2.0
ilnarcgreeras(cid:11)es.Wlineeeaxrlpylafionrthsimsaelflfe(cid:11)c2tbayndnorteimngaitnhsatutnhcehbaanngdewdidfothr mplitude1.5
2 A1.0
of the first pulse limits the number of momentum states dif- o
h
fractedatt=0.As(cid:11) increases,thepulseareaextractedfrom Ec
2 0.5
the fits increases as more high-order momentum states are
rephased. When the second pulse is comparable in duration
0.0
to the first excitation pulse, all higher-order momentum 850 860 870 880 890 900 910
states excited by the first pulse can be rephased. Therefore, (b) T(cid:1)Μs(cid:2)
there is no change in the pulse area extracted from the fits if
the second pulse duration is further increased. We note that FIG.15. Theeffectofvarying(cid:20)onthesignalamplitude.Inthis
the bandwidth of the second standing wave pulse decreases case(cid:20)wasdecreasedbyreducingthedetuningandthesignalshape
isfittoEq.(cid:1)26(cid:2).Thevaluesof(cid:20)are(cid:1)a(cid:2)−0.018and(cid:1)b(cid:2)−0.034.
with increasing pulse duration.Although this reduces the or-
derofrecoilcomponentsthatarerephased,itwouldalsolead
T.Althoughthiseffectisgenerallysmall,asystematicvaria-
to a decrease in measured pulse area which is not observed.
tion in the temporal shift implies a variation in the value of
The measured beam power, spatial profile, and pulse dura-
(cid:5) since the function used to fit the data is not periodic in
tioncanalsobeusedtoinferthepulsearea.Thevalueofthe q
this case. Therefore, high precision studies of (cid:5) rely on
pulse area extracted from fit parameters b and d agrees with q
the experimental value within a factor of 2 for pulse dura-
tions up to (cid:6)400 ns in Fig. 14. 0.0
TotesttheeffectsofSEontheechoamplitude,wevaried
the parameter (cid:20)given in Eq. (cid:1)21(cid:2) by changing the detuning (cid:1)0.2
oSfEthperosdtuancedsinagpwroanvoeupnuclesdesa.sIytmcamnebtreysienenthferoemchoFiagm.1p5littuhdaet (cid:1)Μ(cid:2)s(cid:1)0.4
in the vicinity of the zeros that is predicted by theory. The shift
data is once again fit to Eq. (cid:1)26(cid:2). oral(cid:1)0.6
p
m
Figure 16 shows the associated effect of SE on the tem- Te
poral offset of the T dependent signal. Here (cid:20)is varied by (cid:1)0.8
changingeitherthe(cid:7)or(cid:11).ItisclearonthebasisofEq.(cid:1)21(cid:2)
2
that(cid:20)shoulddependon(cid:7).Asdiscussedlaterinthissection, (cid:1)1.0
(cid:20)is also influenced by (cid:11). In Fig. 16 the temporal offset is
2 0.00 0.02 0.04 0.06 0.08 0.10
extractedfromafittoasinglerecoilperiodinthevicinityof
Θ(cid:1)rad(cid:2)
(cid:6)1 msbasedonEq.(cid:1)26(cid:2).IndependentmeasurementsinRef.
(cid:3)11(cid:4) have shown that the temporal offset does not affect the
FIG. 16. Temporal shift extracted by fitting to a single recoil
recoil frequency. However, in the presence of cloud launch, period.Inthiscasethetemporalshiftwasvariedbychangingthe(cid:7)
asT isvaried,thedetuningsforthetwoexcitationpulsesare and (cid:11).The shift is proportional to the measured (cid:20)parameter.The
2
not the same. In addition, some atoms only sample a limited error bars on the vertical axis are negligible and the error in the
extentofthespatialprofile.Thiscauseschangesinthevalue value of (cid:20)extracted from the fit is (cid:6)5%.The horizontal axis rep-
of (cid:20)extracted from fits taken at different pulse separations, resentstheabsolutevalueof(cid:20)measuredfromthefits.
013610-10