
Generalized Simplified Variable-Scaled Min Sum LDPC decoder for irregular LDPC Codes PDF
Preview Generalized Simplified Variable-Scaled Min Sum LDPC decoder for irregular LDPC Codes
Generalized Simplified Variable-Scaled Min Sum LDPC decoder for irregular LDPC Codes Ahmed A. Emran § and Maha Elsabrouty† Electronics and Electrical Communications Egypt-Japan University for Science and Technology (E-JUST), Alexandria, Egypt Email: {§ahmed.emran, †maha.elsabrouty}@ejust.edu.eg Abstract—In this paper, we propose a novel low complexity factor with iterations. It is simpler than both variable scaling scaling strategy of min-sum decoding algorithm for irregular factor [6] and 2D correction Min-Sum [5] in implementing 5 LDPC codes. In the proposed method, we generalize our pre- and designing. Simulation results show that SVS-min-sum 1 viously proposed simplified Variable Scaled Min-Sum (SVS-min- has lower Bit Error Rate (BER) than constant scaling factor 0 sum) by replacing the sub-optimal starting value and heuristic for many LDPC codes [7]. SVS-min-sum algorithm starts the 2 update for the scaling factor sequence by optimized values. scaling factor sequence with a constant value equals 0.5. This DensityevolutionandNelder-Meadoptimizationareusedoffline, n restriction decreases its performance and makes it unsuitable priortothedecoding,toobtaintheoptimalstartingpointandper a for some codes. iterationupdatingstepsizeforthescalingfactorsequenceofthe J proposed scaling strategy. The optimization of these parameters In this paper, we introduce a generalization of the SVS- 9 proves to be of noticeable positive impact on the decoding min-sum algorithm by removing the restriction of starting 2 performance. We used different DVB-T2 LDPC codes in our the scaling sequence from 0.5. This generalization leads to simulation. Simulation results show the superior performance better performance than constant scaling for all codes. In T] (in both WER and latency) of the proposed algorithm to other fact, constant scaling can be seen as a special sub-optimized Min-Sumbasedalgorithms.Inadditiontothat,generalizedSVS- version of the proposed algorithm as shown in section IV. We I . min-sumalgorithmhasverycloseperformancetoLLR-SPAwith applyNelder-Meadoptimization[8]onDEtojointlyoptimize s much lower complexity. c the initial scaling factor and updating step of the scaling [ sequence. Simulation results illustrate the improvement of the 1 I. INTRODUCTION proposed algorithm in both BER performance and decoding latency over other scaling strategies. v Low-density parity check codes (LDPC) were introduced The rest of the paper is organized as follows: Section II 6 3 by Gallager [1] in the early 1960s. Decoding of LDPC codes, presents the necessary background on the SPA, Min-Sum, 3 by log-likelihood ratio sum-product algorithms (LLR-SPA), ScaledMin-Sum,VariableScaledMin-SumandSVS-min-sum 7 are proven to achieve excellent capacity performance, by algorithms. Section III presents the generalized SVS-min-sum 0 approaching the Shannon bound [2]. However, the drawbacks algorithm. The simulation results are displayed and discussed . of LLR-SPA, namely, the high complexity and sensitivity in Section IV. Finally, the paper is concluded in section V. 1 to linear scaling, are solved by the Min-Sum algorithm 0 [3]. Scaled Min-Sum [4] is a modification of Min-Sum 5 algorithm, where a scaling factor is used to decrease the error 1 : introduced by using the approximate minimum operation. II. REVIEWOFTHESPAANDMIN-SUMBASED v Scaled Min-Sum (with constant scaling factor) is suitable for ALGORITHMS i X regular LDPC codes. However, irregular LDPC codes require different scaling technique [5]–[7]. An (n,k) LDPC code is a binary code characterized by a r a In [5], a two-dimensional (2D) correction of the min-sum sparse parity check matrix H ∈ Fm×n where m = n−k. It 2 was proposed. In this algorithm, different scaling factors can be represented by a Tanner graph which contains variable are required for different check node degrees and variable nodesj ∈{1..n}andchecknodesi∈{1..m}.Wedenotethe node degrees. Consequently, the algorithm requires the set of variable nodes connected to a certain check node i as calculation of two scaling factor vectors α and β with length V{i}. Furthermore, the set V{i}/j denotes the set of variable equal maximum check node’s degree and variable node’s nodes connected to check node i excluding j. Similarly, the degree respectively. These vectors are optimized by parallel set of check nodes connected to a certain variable node j differential optimization of Density Evolution (DE). is denoted by C{j}. C{j}/i denotes the set of check nodes In [6], different scaling factor per iteration is proposed for connected to the variable node j excluding i. irregular LDPC codes. Different scaling factor per iteration LDPC codes are efficiently decoded by message passing de- technique has good performance for irregular LDPC codes. coding algorithms. The main idea behind all message passing However, adding these scaling factors requires complex algorithms is processing the received symbols iteratively in calculationstepsindesigningstage,andrequiresextrastorage concatenated steps that can be seen over the Tanner graph as to store the scaling factor value of each iteration. horizontal step followed by vertical step. In this section, we In [7], we proposed simplified variable-scaled min-sum review some message passing decoding algorithms that are (SVS-min-sum) decoding technique. This algorithm uses either used for comparision or as the starting point of our simply implemented heuristic technique to update the scaling modified algorithm. A. Sum-Product algorithm (SPA) One iteration of the tanh-based SPA is described in the following steps:- 1) Initialization step: The LLR of bit number j is initializedwithitschannelLLR(U ).Theseinitial chj values are used as v , messages from variable j→i node j to check nodes i ∀ i∈C{j}. 2) Horizontal step: At each check node i, messages v (which come from variable nodes V{i}) are j→i usedtocalculatethereplymessagesU forallj ∈ i→j V{i} by (1). (cid:18) (cid:19) U =2×tanh−1 (cid:89) tanhvj(cid:48)→i (1) i→j 2 Fig.1. CircuitrepresentationofSVSscaling j(cid:48)∈V{i}/j 3) Vertical step: At each variable node j, messages TABLEI. CALCULATIONOFSCALINGFACTORVALUEOFEACH U are used to calculate the reply messages v ITERATIONUSINGSVS-MIN-SUMALGORITHM i→j j→i for all i∈C{j} by (2). Iterationindexi α (cid:88) 1→S 0.5 v =U + U (2) j→i chj i(cid:48)→j (S+1)→2S 0.75 i(cid:48)∈C{j}/i (2S+1)→3S 0.875 4) Decision step (3S+1)→4S 0.9375 For each variable node j, its LLR is updated by (3) (cid:88) LLRj =Uchj + Ui(cid:48)→j (3) D. SVS-min-sum algorithm i(cid:48)∈C{j} Changing the scaling factor with iteration for irregular The LLR values are applied to the hard decision to decide on LDPC codes is used in [6]. Despite of performance enhance- the bit value to be 1 if LLRj < 0 and zero otherwise. The ment of this variable scaled min-sum algorithm, it requires syndrome is calculated and checked; if it is all-zero vector, extra storage because we need different scaling factor value this word is successfully decoded, otherwise, if the syndrome periteration,associatedwithdifferentmutualinformationinto condition is not satisfied, the decoder proceeds to the next passedmessagesperiteration[6].Thegeneralfractionalvalues iteration. This process continues till either the code word is (takenbythescalingfactors)makethemultiplicationoperation successfullydecodedorthemaximumiterationsareexhausted. complex to implement. We proposed in [7] an SVS-min-sum algorithmaddressestheparticularpointofsimplyper-iteration B. Min-Sum algorithm updated scaling rule. As stated in [6], the scaling factor should increase exponen- The Min-Sum algorithm follows the same steps as SPA. It tiallywithiterationsanditsfinalvalueis1.Soweapproximate onlyapproximatesthehorizontalstepcalculationbyminimum the scaling factor sequence to a stair sequence which is operation as shown in (4) [3] updated every S iterations, increase exponentially and easy (cid:89) to implement. The variable scaling factor can be calculated U = sign(v )∗ min |v | (4) i→j j(cid:48)→i j(cid:48)→i as: j(cid:48)∈V{i}/j j(cid:48)∈V{i}/j α=1−2−(cid:100)i/S(cid:101) (6) Min-Sum is easier to implement, as it gets rid of the tanh(.) Where(cid:100)i/S(cid:101)isthefirstintegergreaterthanorequaltoi/S .i calculation. However, the approximation of the tanh(.) to the is the iteration index which takes values {1,2,3...}. By using min(.)leadstosomelossofperformancecomparedtothetanh- (6), the scaling factor of each iteration can be calculated as based SPA algorithm. This loss of performance is partially shown in table I. This sequence is:- recovered by Scaled Min-Sum algorithm. 1) Easytodesign,becauseitrequiresasingleparameter C. Scaled Min-Sum algorithm S. 2) Doesnotneedtostoreaspecificscalingsequencefor In order to decrease the gap between the min-sum and the each code rate. It only requires to store the optimal tanh-based SPA algorithms, a constant scaling factor (α < 1) updating step size S of each code rate. is applied to the check node updating equation (4). In other 3) Easy to implement, because it only requires shifting words, converts the Horizontal step to (5) right by (cid:100)i/S(cid:101) then subtraction. Number of required (cid:89) shifts (cid:100)i/S(cid:101) can be stored in a register and increased Ui→j =α sign(vj(cid:48)→i)∗ min |vj(cid:48)→i| (5) by 1 every S iterations. j(cid:48)∈V{i}/j j(cid:48)∈V{i}/j AsshowninFig.1,theSVSscalingstrategyisimplementedby This scaling factor is optimized to maximize the performance two sub-circuits. The first sub-circuit calculates the number of of Scaled Min-Sum algorithm. shifts required in each iteration (cid:100)i/S(cid:101), this number of shifts optimize the initial scaling factor α . To calculate the op- 0 timal (α ,S) , we use Nelder-Mead optimization Method 0 opt. [8] (summarized in III-B) to minimize (E /N ) , where b 0 min (E /N ) is the minimum E /N required to achieve pre- b 0 min b 0 specified BER threshold. (E /N ) of given (α ,S) is b 0 min 0 calculated by DE. A. Density Evolution (DE) of Min-Sum based algorithms DE checks the ability of an LDPC decoder to correctly decode messages with specific noise variance. This is done by tracing the Probability Density Function (PDF) of messages passedbetweencheckandvariablenodes(usingall-zerocode- word). Using of all-zero code-word is valid in Binary Phase Shift Keying (BPSK) because the LLR of both 1 and 0 has Fig.2. CircuitrepresentationofGSVSscaling a similar PDF shape, but this is not valid in Quadrature TABLEII. CALCULATIONOFSCALINGFACTORVALUEOFEACH Amplitude Modulation (QAM) signaling [9]. ITERATIONUSINGGSVS-MIN-SUMALGORITHM DE is used in [2] to obtain the optimal weight distribution of irregular LDPC codes, and is used in [4] [5] to calculate the Iterationindexi α optimal scaling factor(s) of LDPC decoder. We use the same 1→S α0 DE as in [5] after changing the PDF of channel LLR so that (S+1)→2S 0.5+0.5∗α0 we can use it with QAM signaling. (2S+1)→3S 0.75+0.25∗α0 (3S+1)→4S 0.875+0.125∗α0 1)Channel LLR’s PDF of BPSK over an AWGN channel: In BPSK, all-zero code-word’s bits V = 0 are modulated k to x = 1 − 2V = 1. Then x is transmitted over an k k k is calculated by dividing the iteration clock by S (updating Additive White Gaussian Noise (AWGN) channel with noise step) to generate the updating clock of the scaling factor, then variance σ2, so the received sequence is y = 1+n where k k this updating clock is used to count the required number of n is normally distributed random variable with mean=0 and k shifts (cid:100)i/S(cid:101) using a counter starts by 1. The other sub-circuit variance=σ2 .Therefore,thechannelLLR(U =2×y /σ2) multiplies the minimum operation output U(cid:48) by α specified in is normally distributed random variable withchmkean=2/σk2 and (6) by using a Barrel shifter to shift U(cid:48) right by (cid:100)i/S(cid:101) then variance=4/σ2.ThePDFofU isusedastheinitialPDFof subtract. chk variable nodes’ messages to check nodes. 2)Channel LLR’s PDF of higher order QAM constellation III. GENERALIZEDSVS-MIN-SUM(GSVS-MIN-SUM) over an AWGN channel: As shown in [9], for higher order ALGORITHM constellations, we cannot assume that all-zero code-word was AsshownintableI,SVS-min-sumsequencestartswith0.5 transmitted. Therefore, we used a similar procedure to [9], and increases exponentially with iterations. The limitation of whereauthorsmodifiedthedefinitionofbit’sLLRtobe:”LLR starting with a fixed value of 0.5 restricts the performance to of receiving the same bit value as was transmitted” instead of be sub-optimal. As a solution, we propose a new GSVS-min- ”LLR of receiving 0”. This is equivalent to replacing Uch by sbuym(7a)l:gorithmwherethescalingfactorssequenceiscalculated Uifc+ahn,dwohnelryeUifc+Uhkch=k Uhacshkth×e(s1a−m2eVskig).nSaosUgci+vheknwbiyllVbekp.ositive α=1−(1−α )∗2−((cid:100)i/S(cid:101)−1) (7) Firstly, for any constellation point W, we calculate the PDF 0 of U for bit number l into W given that W is transmitted ch Where α is the initial scaling factor. By using (7), scaling f (u /W) [10]. Then we calculate the average PDF of U+ 0 Uch l ch factorofeachiterationiscalculatedasshownintableII,where by (8). scaling factor values start with α and increase exponentially to unity for large value of iteratio0n index i. 1 log2(cid:88)(M)/2(cid:18) (cid:88) f (u)= f (u =u/W) Circuit representation of GSVS scaling is shown in Fig. Uc+h η Uch l 2. It is similar to SVS scaling circuit, but with two main l=1 W∈Zl (cid:19) differences: the first difference is that U(cid:48) is multiplied by (cid:88) + f (u =−u/W) (8) (1 − α ) before shifting right, this is added to generalize Uch l 0 the initial scaling factor. (1 − α ) is chosen to be simply W∈Ol 0 implemented. We use (1−α ) to be in the form of 2−i or Where l is the bit position index. Only half of bit positions 0 2−j+2−k,wherei,j andk areintegernumbers;forexample, were used, because of symmetry between real and imaginary ifi=2→(1−α )=0.25,i=3→(1−α )=0.125andif axes of QAM signaling. Z is the set of W where bit position 0 0 l j =2,k =3→(1−α )=0.375 . The second difference is l contains 0. O is the set of W where bit position l contains 0 l that the counter of required shifts starts with 0 instead of 1 1. η is PDF correction factor used to ensure that area under because GSVS-min-sum requires ((cid:100)i/S(cid:101)−1) shifts not (cid:100)i/S(cid:101) the PDF=1. as in SVS-min-sum. In other words, calculate the average PDF of U for zeros ch In SVS-min-sum, we only need to optimize the updating and −U for ones. Then use this PDF as the initial PDF of ch step size S, however, in GSVS-min-sum we also need to variable nodes’ messages. Fig.4. contoursof(Eb/N0)min forshortcodewithrate=0.5 Fig.5. WERof(16200,7200)LDPCover256QAMwithdifferentdecoding algorithms Fig.3. FlowchartofNelder-Meadmethod S = 10 [7], Scaled Min-Sum with α = 15/16 (optimized by B. Nelder-Mead (NM) optimization method DE and the same as in [7]), GSVS-min-sum with (α =0.75 0 and S =9) (optimized by DE with Nelder-Mead method) and NM optimization [8] of (α ,S) is based on constructing 0 2D correction min-sum; where the output of the check nodes a simplex (polygon) of 2+1=3 random solution points {X = i with degree 4,5,6 and 7 is multiplied by 0.94, 0.92, 0.88 and (α ,S) |i = 1,2 or 3} for our 2-dimension problem. After 0 i 0.86 respectively, and the output of the variable nodes with calculating (E /N ) of these three points, the worst point b 0 min degree 1,2,3 and 8 is multiplied by 1.00, 1.00, 0.91 and 0.83 is replaced by a better point as described in the flow chart respectively [5]. Results in Fig.5 show that: in Fig.3. This procedure is repeated until the simplex shrink enough to the optimal solution. • GSVS-min-sum has better performance than SVS- We use Nelder-Mead method for many reasons: first, it min-sum by 0.5 dB at WER= 10−3, this indicates the does not need the mathematical derivative of the cost func- importance of the proposed algorithm, which jointly tion (which is not available because our cost function is optimizes the initial scaling factor α with the updat- 0 (E /N ) which comes from DE). Second, Nelder-Mead ing step size S. b 0 min is faster in convergence than other heuristic methods. Finally, • Although 2D correction min-sum has an excellent our cost function has only one minimum, so the algorithm performanceaftermanyiterations(200iterations)[5], does not get trapped in a local minimum. To prove the last it has higher WER than GSVS-min-sum algorithm claim that (E /N ) has only one minimum, we calculated b 0 min after 40 iterations for the whole simulation range and it for all possible combinations of (α ,S) for short length 0 higher than scaled-min-sum for high E /N range. LDPC code with rate 0.5 specified in DVB-T2. Fig.4 shows b 0 The gap between GSVS-min-sum and 2D correction that (E /N ) has only one minimum. Similar results b 0 min is 0.3 dB at WER= 10−3. are obtained for all tested codes. Optimization of (α ,S) is 0 calculated offline for each LDPC code rate, then the optimal • There is a small gap between GSVS-min-sum and value is used to implement the decoding circuit. LLR-SPA performances (0.1 dB for low E /N and b 0 nearly disappears at high E /N ), with much lower b 0 IV. SIMULATIONENVIRONMENTANDRESULTS implementation complexity. For simulation, we used (16200, 7200) eIRA LDPC code • For the scaled min-sum algorithm, Optimizing the specified in DVB-T2 standard [11], [12]. Data are produced scaling factor of each code rate increases its per- as binary bits modulated using the challenging 256-QAM formance specially for high Eb/N0. This concept is modulationschemeandsentoveranAWGNchannel.Thesim- illustrated in [7] by showing that each code rate of ulations are performed using MATLAB platform. Maximum DVB-T2 LDPC codes has different optimal scaling number of iterations is set to 40 iterations. factor. Fig.5 shows the WER of LLR-SPA, SVS-min-sum with Fig.6showsclearlythatGSVS-min-sumnotonlyhaslower TABLEIII. OPTIMALPARAMETERSOFDIFFERENTLDPCDECODING ALGORITHMSFORBPSK constantα stepofSVS (α0,S)ofGSVS (16200,7200) 0.9375 5 (0.75,9) (16200,11880) 0.875 10 (0.75,16) (64800,48600) 0.875 10 (0.75,18) Fig.6. Averagenumberofiterationsof(16200,7200)LDPCover256QAM withdifferentdecodingalgorithms WER than other min-sum based algorithms, but also it has the lowest average number of iterations which leads to lower latency and higher average throughput. For more results, we used three different rates of the Fig.7. WERofdifferentLDPCcodsoverBPSK LDPC codes specified in DVB-T2 standard with BPSK, these codes are (16200,7200) short code with nominal rate = 0.5, (16200,11880) short code with nominal rate = 0.75 REFERENCES and (64800,48600) normal code with rate = 0.75. WER of [1] R.Gallager,“Low-densityparity-checkcodes,”InformationTheory,IRE these codes with constant scaled-min-sum, SVS-min-sum and Transactionson,vol.8,no.1,pp.21–28,1962. GSVS-min-sum decoding algorithm are shown in Fig. 7. Sim- [2] D. J. MacKay, “Good error-correcting codes based on very sparse ulation results show that GSVS-min-sum has the lowest WER matrices,” Information Theory, IEEE Transactions on, vol. 45, no. 2, amongthethreedecodingalgorithms,eventhoughscaledmin- pp.399–431,1999. sum has lower WER than SVS-min-sum or not. Note that: [3] M. P. Fossorier, M. Mihaljevic, and H. Imai, “Reduced complexity constant scaling (in scaled min-sum) and SVS-min-sum are iterative decoding of low-density parity check codes based on belief special cases of the GSVS-min-sum where S= number of propagation,” Communications, IEEE Transactions on, vol. 47, no. 5, pp.673–680,1999. iterations for scaled min-sum and α = 0.5 for SVS-min- 0 [4] J.ChenandM.P.Fossorier,“DensityevolutionfortwoimprovedBP- sum.SoGSVS-min-sum,whichhasoptimizedvaluesforboth based decoding algorithms of LDPC codes,” Communications Letters, α and S, has the best performance between them as shown 0 IEEE,vol.6,no.5,pp.208–210,2002. in Fig. 7. The parameters of the three decoding algorithms [5] J. Zhang, M. Fossorier, D. Gu, and J. Zhang, “Improved min-sum are shown in table III. For (16200,11880) code, GSVS-min- decodingofLDPCcodesusing2-dimensionalnormalization,”inGlobal sum has the same performance as constant scaling factor and TelecommunicationsConference,2005.GLOBECOM’05.IEEE,vol.3. better performance than SVS-min-sum. The poor performance IEEE,2005,pp.6–8. of SVS-min-sum comes from the limitation of starting by 0.5 [6] G. Lechner and J. Sayir, “Improved sum-min decoding for irregular LDPCcodes,”inTurboCodes&RelatedTopics;6thInternationalITG- whichisawayfromtheoptimalscalingsequence.Fortheother Conference on Source and Channel Coding (TURBOCODING), 2006 codes,GSVS-min-sumhasbetterperformancethanbothSVS- 4thInternationalSymposiumon. VDE,2006,pp.1–6. min-sum and constant scaled min-sum. [7] A. A. Emranand M. Elsabrouty, “Simplified variable-scaledmin sum LDPC decoder for irregular LDPC codes,” in Consumer Communica- tionsandNetworkingConference,2014.CCNC2014.11thIEEE,Jan V. CONCLUSIONANDFUTUREWORK 2014,pp.526–531. Inthispaper,wegeneralizedtheSVS-min-sumdecoderby [8] J.A.NelderandR.Mead,“Asimplexmethodforfunctionminimiza- tion,”Thecomputerjournal,vol.7,no.4,pp.308–313,1965. allowingittostartwithanyinitialscalingfactorα .Simulation 0 [9] H. M. Tullberg and P. H. Siegel, “Serial concatenated TCM with an resultsindicatedthesuperiorperformanceandlowerlatencyof inneraccumulatecode-partii:density-evolutionanalysis,”Communica- GSVS-min-sumdecodertoothermin-sumbasedalgorithms.In tions,IEEETransactionson,vol.53,no.2,pp.252–262,2005. addition, GSVS-min-sum algorithm performance is very close [10] M. Benjillali, L. Szczecinski, and S. Aissa, “Probability density func- to the LLR-SPA with much lower complexity. Moreover, the tions of logarithmic likelihood ratios in rectangular QAM,” in Com- proposed algorthim is still simpler to implement than both munications, 2006 23rd Biennial Symposium on. IEEE, 2006, pp. the variable scaling factor in [6] and the 2D correction Min- 283–286. Sumin[5].Asfuturework,wewillapplyourGSVS-min-sum [11] D. BlueBook, “A122 (2008, june). framing structure, channel coding and modulation for a second generation digital terrestrial television decoding algorithm to layered LDPC codes implementation. broadcastingsystem(DVB-T2).” [12] ——, “A133.(2009). implementation guidelines for a second genera- ACKNOWLEDGMENT tiondigitalterrestrialtelevisionbroadcastingsystem(DVB-T2),”DVB technicalreport,Tech.Rep. This work is supported by E-JUST and Minister of High Education (MoHE). And is supported by NTRA as part of the project ”Design and implementation of DVB-T/T2 solution”.
The list of books you might like

The Strength In Our Scars

Credence

Shatter Me Complete Collection (Shatter Me; Destroy Me; Unravel Me; Fracture Me; Ignite Me)

Corrupt (Devil's Night #1)

Convergent close-coupling calculations of two-photon double ionization of helium

Constraints on UED KK-neutrino dark matter from magnetic dipole moments

SQE Services Agreement

The Bright Book of Life

DTIC ADA456128: Evaluation of Human-Robot Interaction Awareness in Search and Rescue

Extraordinary Gazette of India, 2006, No. 516

Extraordinary Gazette of India, 2006, No. 528

Agnes

Journal of the Barber Coin Collectors' Society

Bylaw 31-14

Ilmu Dakwah: Kajian Ontologi, Epistemologi, Aksiologi dan Aplikasi Dakwah

Bürgerliches Recht II. Schuldrecht Allgemeiner Teil, 3. Auflage
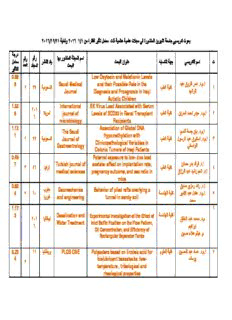
2016 / 12 / 21 ولغاية 2016 1 1

Einstein Product Metrics in Diverse Dimensions
![Verrassing: verliefd! (Wrangler's Creek 02)[Feelgood 18] book image](https://cdn-3.pdfdrive.to/media/content/thumbnails/17318296.jpg)
Verrassing: verliefd! (Wrangler's Creek 02)[Feelgood 18]





