ERIC EJ913377: Transitional and Steady-State Choice Behavior under an Adjusting-Delay Schedule PDF
Preview ERIC EJ913377: Transitional and Steady-State Choice Behavior under an Adjusting-Delay Schedule
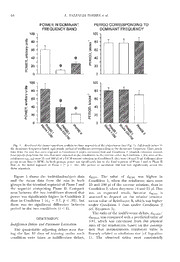
JOURNALOFTHEEXPERIMENTALANALYSISOFBEHAVIOR 2011,95,57–74 NUMBER1(JANUARY) TRANSITIONAL AND STEADY-STATE CHOICE BEHAVIOR UNDER AN ADJUSTING-DELAY SCHEDULE L. VALENCIA TORRES, S. DA COSTA ARAU´JO, C.M. OLARTE SANCHEZ, S. BODY, C.M. BRADSHAW, AND E. SZABADI UNIVERSITYOFNOTTINGHAM Twelveratsmaderepeatedchoicesonanadjusting-delayschedulebetweenasmallerreinforcer(A)that wasdeliveredimmediatelyafteraresponseandalargerreinforcer(B)thatwasdeliveredafteradelay whichincreasedordecreasedby20%dependingonthesubject’schoicesinsuccessiveblocksoftrials. Intwo phasesoftheexperiment(100sessionsand40sessions),reinforcer sizeswereselectedwhich enabledtheoreticalparametersexpressingtherateofdelaydiscountingandsensitivitytoreinforcersize tobeestimatedfromtheratiooftheindifferencedelaysobtainedinthetwophases.Indifferencedelays, calculatedfromadjustingdelaysinthelast10sessionsofeachphase,wereshorterwhenthesizesofA andBwere14and25mlofa0.6Msucrosesolutionthanwhentheywere25and100mlofthesame solution.Theratiooftheindifferencedelayswassignificantlysmallerthanthatpredictedonthebasisof anassumedlinearrelationbetweenreinforcersizeandinstantaneousreinforcervalue,consistentwitha previous proposal that this relation may be hyperbolic in form. Estimates of the rate of delay discountingbasedontheratioofthetwoindifferencedelays(mean,0.08s21)weresimilartovalues obtained previously using different intertemporal choice protocols. Estimates of the size-sensitivity parameter(mean113ml)weresimilartoestimatesrecentlyderivedfromperformanceonprogressive- ratioschedules.Inbothphasesoftheexperiment,adjustingdelaysinsuccessiveblocksoftrialswere analyzed using the Fourier transform. The power spectrum obtained from individual rats had a dominantfrequencythatcorrespondedtoaperiodofoscillationoftheadjustingdelaybetween30and 100trialblocks(mean,78).Powerinthedominantfrequencybandwashighestintheearlysessionsof thefirstphaseanddeclinedwithextendedtraining.Itissuggestedthatthisexperimentalprotocolmay haveutilityinneurobehavioralstudiesofintertemporalchoice. Keywords: intertemporalchoice,adjusting-delayschedule,delaydiscounting,reinforcermagnitude, Fouriertransform,leverpress,rat _______________________________________________________________________________ In an intertemporal choice schedule, the where q and q are the sizes of the two A B subjectchoosesbetweenreinforcersthatdiffer primary reinforcers, d and d are the delays A B with respect to their sizes and delays. For associated with each alternative, and K is a example,asubjectmaybeconfrontedwithtwo parameter expressing the rate of delay dis- operanda,AandB;ifitrespondsonA,asmall counting.Itisassumedthatwhenfacedwitha reinforcer will bedelivered after ashort delay, choicebetweenAandB,thesubjectselectsthe whereasifitrespondsonB,alargerreinforcer outcome that has the higher overall value at will be delivered after a longer delay. themomentofchoice.Itshouldbenotedthat According to one model of intertemporal V refers not to the value of the primary choice behavior (Mazur, 1987, 2001, 2006), reinforcer, but to the overall value of the the reinforcing value of each outcome is a conditioned reinforcing stimuli that are pres- declining hyperbolic function of the delay ent at the moment of choice. Thus Equations interposed between the response and the 1a and 1b do not imply that the primary primary reinforcer. reinforcer itself is devalued as a function of delay (Mazur, 1995). 1 1 V ~q : ; V ~q : , ð1a;1bÞ Equations 1a and 1b imply direct propor- A A 1zK:dA B B 1zK:dB tionality between value and the size of a reinforcer. However, there is emerging evi- dence for a nonlinear relation between value We are grateful to Mrs. V.K. Bak for skilled technical assistance. and reinforcer size (Mazur & Biondi, 2009; Address correspondence to C. M. Bradshaw, Psycho- Rickard, Body, Zhang, Bradshaw, & Szabadi, pharmacologySection,DivisionofPsychiatry,Universityof 2009), in keeping with the economic concept Nottingham, Queen’s Medical Centre, Nottingham, NG7 of diminishing marginal utility (Killeen, 2009; 2UH,U.K.(e-mail:[email protected]). doi:10.1901/jeab.2011.95-57 Pine, et al., 2009). Ho, Mobini, Chiang, 57 58 L. VALENCIA TORRES et al. Bradshaw and Szabadi (1999) proposed a temporal choiceinhumans(Hinvest & Ander- modification of Equations 1a and 1b to take son,2010;Liang,Ho,Yang,&Tsai,2010). intoaccountthepossibilityofsuchanonlinear A significant practical difficulty with the relation. Ho et al. (1999) posited a hyperbolic applicationofEquation3isthelengthoftime relation, in which the effect of reinforcer needed to collect sufficient data to fit the magnitude on value is modulated by a single linearfunctions,becauseeachvalueofd is B(50) ‘‘size-sensitivity parameter’’, Q: derived from steady-state performance using a different value of d , which, in the case of 1 1 A V ~ : ; animal subjects, may require 40–60 training A 1zQ=qA 1zK:dA sessions, and five or six dB(50)/dA pairs are needed to obtain a reliable linear function 1 1 VB~1zQ=q :1zK:d : ð2a;2bÞ (see, for example, Kheramin et al., 2002). B B Since neurobehavioral experiments involving cerebral lesions typically entail two or more groups of 10 or more subjects, it is clear that By experimentally manipulating the delays this kind of experiment is very costly in terms and/or sizes of A and B, a point of indiffer- of both time and money. ence may be determined at which the subject One purpose of this paper is to describe an shows no preference for either outcome. It is abbreviated approach to estimating Q and K generally assumed that indifference implies based on Equation 3, which requires the that V 5 V . Equating the right-hand sides of A B determination of only two values of d . Equations 2a and 2b and rearranging the B(50) The logic of the method is as follows. If the terms yields the following linear relation smaller of the two reinforcers is delivered between the indifference delay to the larger immediately(i.e.d <0),Equation3becomes reinforcer, d , and the delay to the smaller A B(50) reinforcer, dA (Ho et al., 1999): d ~ 1 :(cid:1)Q=qA{Q=qB(cid:2): ð3aÞ 1 (cid:1)Q=q {Q=q (cid:2) 1zQ=q B(50) K 1zQ=qB d ~ : A B zd : A: ð3Þ B(50) K 1zQ=q A 1zQ=q B B Equation 3a isthe limit of Equation 3 asd R A 0. If two indifference delays are determined This relation can be used to examine the using different pairs of reinforcer sizes (q , effectsofneurobiologicalinterventionsonthe A1 q , and q , q ), then the ratio of the hypothetical processes of delay discounting B1 A2 B2 indifference delays is and sensitivity to reinforcer size. For example, aifrethheeslidzecsoonfstRaenitnfaonrdceirnsdAiffaenrdenBce(qdAealanyds aqrBe) ddB(50)1~11==qqA1{{11==qqB1:11zzQQ==qqB2: ð4Þ B(50)2 A2 B2 B1 determined for a seriesof delays to Reinforcer A (d ), a change in the slope of Equation 3 A Ifreinforcersizesareselectedsuchthat(1/q A1 inducedbyacerebrallesionimpliesachangein 2 1/q ) 5 (1/q 2 1/q ), Equation 4 B1 A2 B2 Q(i.e.,achangeinsensitivitytoreinforcersize), simplifies to whereas a change in the intercept without a concomitant change in slope implies a change dB(50)1~1zQ=qB2, or in K (i.e., a change in the rate of delay d 1zQ=q B(50)2 B1 discounting, Ho et al., 1999; Mazur, 2006). Using this approach it has been found that Q~ dB(50)1=dB(50)2{1 : excitotoxic and dopamine-depleting lesions of 1=qB2{(dB(50)1=dB(50)2)=qB1 ð4aÞ the orbital prefrontal cortex increase both Q and K (Kheramin, et al., 2002, 2004), whereas Q may thus be estimated empirically from the destruction of the core of the nucleus accum- ratio of the indifference delays, and this bens or disconnection of the nucleus accum- estimateofQmaybesubstitutedintoEquation bensfromtheorbitalprefrontalcortexproduc- 3ainordertoderiveanestimateofKforeach esaselectiveincreaseinK(Bezzinaetal.,2007, value of d . B(50) 2008). Equation 3 has also been applied ThederivationofEquations3and4isbased successfully in experimental studies of inter- on an assumed hyperbolic relationship be- ADJUSTING-DELAY SCHEDULE 59 tween value and reinforcer size, as postulated ior in the adjusting-delay schedule based on in Equations 2a and 2b (Ho et al., 1999). analysis of the power spectrum of cyclical However, a simpler version of Equation 4 may changes in the adjusting delay. be derived from Equation 1, which assumes strict proportionality between value and rein- METHOD forcer size. In this case, the ratio of two indifference delays is given by Subjects d q {q q Twelve experimentally naive female Wistar B(50)1~ B1 A1: A2 ð5Þ rats (Charles River UK) approximately d q q {q B(50)2 A1 B2 A2 4 months old and weighing 250–300 g at the start of the experiment were used. They were Equation 5 contains no free parameters, and housed individually under a constant cycle of therefore yields a specific numerical predic- 12hrlightand12hrdarkness(lighton0600– tion for the ratio of the two indifference 1800hr),andweremaintainedat80%oftheir delays.Asecondaimofthisexperimentwasto initial free-feeding body weights throughout examine whether the empirically obtained theexperimentbyprovidingalimitedamount ratios of the indifference delays would be of standard rodent diet after each experimen- compatible with this prediction. talsession.Tapwaterwasfreelyavailableinthe In the present experiment, indifference home cages. delays were determined using an adjusting- delayschedule(Mazur,1987).Inthisschedule Apparatus thedelaytothelargeroftworeinforcersvaries The rats were trained in standard operant in accordance with the subject’s choice. For conditioning chambers (CeNeS Ltd, Cam- example, if, in a block of trials, the subject bridge,UK)ofinternaldimensions253 253 shows a preference for the larger reinforcer 22 cm. One wall of the chamber contained a (B),thedelaytothatreinforcerisincreasedin centralrecesscoveredbyahingedclearPerspex the following block; conversely, if it shows a flap,intowhichaperistalticpumpcoulddeliver preference for the smaller reinforcer (A), the a0.6Msucrosesolution.Twoaperturessituated delay to Reinforcer B is reduced in the 5 cm above and 2.5 cm to either side of the following block. The principal dependent recess allowed insertion of motorized retract- variable, the adjusting delay to the larger able levers (CeNeS Ltd, Cambridge, UK) into reinforcer (d ), is seen to oscillate during an B thechamber.Theleverscouldbedepressedby extended period of training, the amplitude of a force of approximately 0.2 N. The chamber oscillation gradually declining as d approach- B wasenclosedinasound-attenuatingchestwith esaquasi-stablevalue;thisquasi-stablevalueof additionalmaskingnoisegeneratedbyarotary d is usually taken to represent the indiffer- B fan. No houselight was present during the ence delay, d (Mazur 1987, 1988). Adjust- B(50) sessions. An Acorn microcomputer pro- ing-delayscheduleshavebeenusedextensively grammed in Arachnid BASIC (CeNeS Ltd, in behavior analytic studies of intertemporal Cambridge,UK)locatedinanadjoiningroom choice (e.g. Green, Myerson, Shah, Estle, & Holt, 2007; Mazur, 1987, 1988, 1994, 1995, controlled the schedules and recorded the behavioraldata. 1996, 2000, 2005), but less often in neurobe- havioral experiments (da Costa Arau´jo et al., Procedure 2009; Mobini et al., 2000). A potential advan- tage of adjusting-delay schedules in neurobe- The experiment was carried out in accor- havioralinvestigationsofintertemporalchoice dance with UK regulations governing experi- is that, in addition to generating quasi-stable ments on living animals. indifference delays, the pattern of oscillation At the start of the experiment the food of the adjusting delay may also provide deprivation regimen was introduced and the information about the effects of neurobiolog- rats were gradually reduced to 80% of their ical interventions on the organism’s adapta- free-feeding body weights. They were then tion to changing delays to reinforcement. An trained to press two levers (A and B) for the additional purpose of this paper is to describe sucrose reinforcer (50 ml, 0.6 M), and were a novel way of quantifying transitional behav- exposed to a discrete-trials continuous rein- 60 L. VALENCIA TORRES et al. forcement schedule in which the two levers The experiment consisted of two Phases (I were presented in random sequence for three and II), the first lasting 100 sessions and the sessions. Then they underwent daily 42-min second 40 sessions. There were two experi- training sessions under the discrete-trials mental Conditions (1 and 2); for half the rats adjusting-delay schedule for the remainder of Condition 1 was in effect in Phase I and the experiment. Each experimental session Condition 2 in Phase II; for the other rats the consisted of seven blocks of four trials. The orderofconditionswasreversed.InCondition trials were 90 s in duration. The first two trials 1, the sizes of the two reinforcers (volume of of each block were forced-choice trials in 0.6 M sucrose solution) were q 5 25 ml and A1 which each lever was presented alone in q 5 100 ml; in Condition 2, the sizes of the B1 random sequence. The other two trials were reinforcerswereq 514mlandq 525ml.In A2 B2 free-choice trials in which both levers were thefirstblockofthefirstsessionofeachphase, presented. The beginning of each trial was d was set at 0.75 s. B signaled by illumination of the central light Experimental sessions were carried out above the reinforcer recess. After 2.5 s the 7 days a week, at the same time each day, leverorlevers(dependingonthetypeoftrial) during the light phase of the daily cycle were inserted into the chamber. When a lever (between 0800 and 1400 hr). press occurred, the lever(s) were withdrawn, the central light was extinguished, and the Data Analysis light located above the lever that had been Indifferencedelaysandparameterestimation.For depressed was illuminated. This light re- each rat, the mean value of d in the last 10 mained illuminated until the delivery of the B sessions of each phase was taken as the reinforcer, and was then extinguished. The indifference delay, d . These data were chamber remained in darkness until the start B(50) analyzed by a two-factor analysis of variance ofthefollowingtrial.Ifnoleverpressoccurred [condition (1,2) 3 order of condition (1-first within 5 s of the lever(s) being inserted, the vs. 2-first)] with repeated measures on the lever(s) were retracted and the central light former factor. As this analysis showed no extinguished. (This seldom happened except significant main effect of order and no during the first few training sessions.) A significant order 3 condition interaction, the response on Lever A resulted in immediate order factor was ignored in all further treat- delivery of the smaller reinforcer, of size q A ment of the data. The ratio of the values of (i.e.d <0).AresponseonLeverBinitiateda A d obtained under the two conditions was delay d whose duration was increased or B(50) B calculated for each rat, and these values were decreased systematically from one trial block usedtocalculateestimatesofQasdescribedin to the next as a function of the choices in the the Introduction, using the formula prior block; at the end of this delay the larger rpeoisniftoiorncesr,ofoLfevseizres AqB,anwdasBd(elelifvterves.d.rigThhte) Q~ dB(50)1=dB(50)2{1 , 1=25{(d =d )=100 were counterbalanced across subjects. B(50)1 B(50)2 Ineachblockoftrials,thedelaytothelarger 100 and 25 being the sizes of Reinforcer B reinforcer, d , was determined by the rat’s B (volumes of 0.6 M sucrose, in ml) in the two choices in the free-choice trials in the preced- conditions of the experiment (q and q , ing block. If Lever A was chosen in both free- B1 B2 respectively). This estimate of Q was used to choicetrialsofblockn,d wasreducedby20% B derive an estimate of K for each rat by in block n+1; if Lever B was chosen in both substitution into Equation 3a. free-choice trials of block n, d was increased B The obtained ratios of the indifference by 20% in block n+1; if Lever A and Lever B delays were also compared with the ratio were each chosen in one free-choice trial in predicted on the basis of an assumed linear blockn,d remainedunchangedinblockn+1. B relation between reinforcer size and instanta- The value of d in the first block of each B neous value. Based on Equation 1, the sessionwasdeterminedinthesamewaybythe indifference delay is choicesmadeinthefinalblockoftheprevious wseesrseiosne.tMatax6i0msuamndan0d.75msi.nimum values of dB dB(50)~ 1 :qB{qA: K q A ADJUSTING-DELAY SCHEDULE 61 Substitutingtheactual reinforcersizes used in significant effect of the order of conditions thisexperimentintothisequation,theratioof (F 5 1.3, p . .1) and no significant 1,10 the indifference delays should be interaction (F 5 2.7, p . .1). Accordingly, 1,10 the data from all 12 rats were pooled in all d 100{25 14 B(50)1~ : ~3:81: subsequentanalyses.Figure 2(right-handpan- dB(50)2 25 25{14 el) shows the ratios of the two values of dB(50); thehorizontallineindicatestheratiopredicted (cf. Equation 5: Introduction). The obtained on the basis of an assumed linear relation ratios were compared with this theoretical between reinforcer size and reinforcer value value using a t-test. (3.81:seeDataAnalysissectionintheMethod). Transitionalbehavior.Inordertocharacterize Theobservedratio(mean6SEM:2.3460.19) the pattern of oscillation of dB during the wassignificantlylowerthanthepredictedratio course of training, a power spectrum analysis (t 57.6,p,.001). 11 wascarriedoutonthevaluesofdBobtainedin The ratios of the dB(50)s were used to each trial block during each phase of the compute estimates of the two parameters of experiment. The method is illustrated in Equation2,QandK.Theresultsofthisanalysis Figure 1. Plots were obtained of log dB versus are shown in Figure 3. There was one clear blocks of trials (Phase I, 700 blocks; Phase II, outlier in the case of both parameters, this 280 blocks: see upper panel of Figure 1). being the rat that showed no difference These data, expressed as deviations from the between the d s in the two conditions (see B(50) mean value of dB, were subjected to a Fourier above).Theparameterthatexpressessensitivity transform (Spike-2, version 4.23: Cambridge to reinforcer size (Q) was derived by substitu- Electronic Design, Ltd) in order to derive tionoftheratiooftheindifferencedelaysinto power spectra (power vs. frequency: see lower Equation 4a. The group mean value of Q (6 panels of Figure 1). The reciprocal of the SEM)was113.8627.9ml.Estimatesofthedelay frequency is the cycle time (period) of discounting parameter (K) were derived by oscillation of d , in blocks. The power of the substitutingeachrat’sestimatedvalueofQinto B dominant frequency of the spectrum within Equation 3a. The group mean value (6 SEM) the frequency range of 0.01 (period 5 100 was0.08260.012s21. blocks)and0.04(period525blocks)andthe length of the period corresponding to the Transitional Behavior dominant frequency were derived for each rat Inall12rats,theadjustingdelaytothelarger in each phase of the experiment (da Costa reinforcer,d ,showedanoscillatingpatternof B Arau´jo et al., 2009). Inspection of the data change during the early stages of training, the indicated that the amplitude of oscillation of amplitudeoftheoscillationstendingtodecline d declinedduringthe100sessionsofPhaseI. B during extended training (see Figure 1 for an This impression was tested by comparing the example;thedatafromall12ratsareshownin power spectra derived from the first and final theAppendix).Powerspectrawerederivedfor 280 blocks of trials of Phase I; comparisons eachrat’sdatafromthreesegmentsoftraining: were also made between the spectra derived thefirstandlast280trialblocksofPhaseIand from the final 280 blocks of Phase I and the the 280 blocks of Phase II. The power in the 280 blocks that comprised Phase II. dominant frequency band and the period correspondingtothedominantfrequencyfrom each segment are shown in Figure 4 (upper RESULTS panels:ratsexposedtoCondition1[q 525ml, A1 Indifference Delays and Parameter Estimation q 5100ml]inPhaseIandCondition2[q 5 B1 A2 Figure 2 (left-hand panel) shows the values 14ml,q 525ml]inPhaseII;lowerpanels:rats B2 of d derived from the last 10 sessions of exposed to the two conditions in the reverse B(50) eachphase.Inallbut1ofthe12rats,thevalue order). ofd (Condition1:q 525ml,q 5100ml) In both groups of rats, power in the B(50)1 A1 B1 washigherthanthatofd (Condition2:q dominant frequency band (Figure 4, left pan- B(50)2 A2 5 14 ml, q 5 25 ml). Analysis of variance els)wasgreatestintheinitialsegmentofPhase B2 indicated that there was a significant effect of I. Analysis of variance showed a significant condition (F 5 28.3, p , .001), but no maineffectofsegment(F 529.7,p,.001), 1,10 2,20 62 L. VALENCIA TORRES et al. Fig. 1. Exampleofonerat’sperformanceontheadjusting-delayscheduleduringtheentireexperiment,illustrating themethodsofdataanalysis.Uppergraph:Adjustingdelaytothelargerreinforcer(d s)plottedagainstblocksoftrialsin B, thetwophasesoftheexperiment.InPhaseI(trialblocks1–700),thesizesofthereinforcers(q ,q )were25and100mlof A B a0.6Msucrosesolution;inPhaseIItheywere14and25ml.ThesegmentsA,B,andC,demarcatedbythebrokenlines, comprisethefirst(A)andfinal(B)280blocksofPhaseIandthe280blocksofPhaseII(C)thatwereusedintheFourier transformanalysis.Theshorthorizontallinesindicatethemeanvaluesofd inthefinal10sessions(70blocks)ofthetwo B phases (d and d ). Lower panels: Power spectra derived from Fourier transform analysis of the d data from B(50)1 B(50)2 B segmentsA,B,andC(seeabove).Powerisplottedagainstfrequency(blocks21).Theperiodofoscillationcorresponding tothedominantfrequencyband,andthepowerwithinthatband,areshownforeachsegment. but no significant effect of group (F 5 2.9, segmentofPhaseI.Theperiodcorresponding 1,10 p..05)andnosignificantinteraction(F 5 to the dominant frequency (Figure 4, right 2,20 4.1, p . .05). In both groups, power was panels) showed no significant effects of seg- significantlylowerinthelastsegmentofPhase ment or group, and no significant interaction I and in Phase II compared to the initial (all Fs , 1). ADJUSTING-DELAY SCHEDULE 63 Fig. 2. A.Valuesofd (s)obtainedunderthetwoconditions.Columnsaregroupmeandata;connectedpoints B(50) aredatafromindividualrats.d wassignificantlylongerunderCondition1(reinforcersizes:q 525ml,q 5100ml) B(50) A B thanunderCondition2(reinforcersizes:q 514ml,q 525ml).B.Ratioofthevaluesofd obtainedunderthetwo A B B(50) conditions.Columnshowsthegroupmeanratio(+SEM);opencirclesshowdatafromindividualrats.Horizontalbroken lineshowstheexpectedratiobasedontheassumptionthatreinforcervalueislinearlyrelatedtoreinforcersize(seetext). Fig. 3. EstimatesoftheparametersofEquation2expressingtherateofdelaydiscounting,K(s21),andsensitivityto reinforcersize,Q(mlofthe0.6Msucrosesolution).Columnsaregroupmeandata(+SEM);opencirclesshowestimates forindividualrats.(Inthecaseofbothparameters,theoutlieristheratthatproducedthelowestratioofthetwovalues ofd :seeFig.2.) B(50) 64 L. VALENCIA TORRES et al. Fig. 4. Resultsofthepowerspectrumanalysisinthreesegmentsoftheexperiment(seeFig.1).Leftpanels:powerin thedominantfrequencyband;rightpanels:periodofoscillationcorrespondingtothedominantfrequency.Upperpanels: datafromtheratsthatwereexposedtoCondition1(opencolumns)firstandCondition2(shadedcolumns)second; lowerpanels:datafromtheratsthatwereexposedtotheconditionsinthereverseorder.InCondition1,thesizesofthe reinforcers(q ,q )were25and100mlofa0.6Msucrosesolution;inCondition2,theywere14and25ml.Columnsshow A B groupmeandata(+SEM).Inbothgroups,powerwassignificantlylessinthefinalsegmentofPhaseIandinPhaseII than in the initial segment of Phase I (* p , .05). The period of oscillation did not vary significantly across the threesegments. Figure 5 shows the individual-subject data d . The value of d was higher in B(50) B(50) and the mean data from the rats in both Condition 1, when the reinforcer sizes were groupsintheterminalsegmentofPhaseIand 25 and 100 ml of the sucrose solution, than in the segment comprising Phase II. Compari- Condition2,whentheywere14and25ml.This sons between the two conditions showed that was an expected result, because d is B(50) power was significantly higher in Condition 2 assumed to depend on the relative instanta- than in Condition 1 (t11 5 3.7, p , .01), but neousvalueofReinforcerB,whichwashigher there was no significant difference between under Condition 1 than under Condition 2 period in the two conditions (t , 1). (cf. Equation 3). Theratiooftheindifferencedelays,d / B(50)1 d ,wascomparedwithapredictedvalueof DISCUSSION B(50)2 3.81, which was calculated from the physical Indifference Delays and Parameter Estimation sizes of the reinforcers, based on the assump- The quasi-stable adjusting delays seen dur- tion that instantaneous reinforcer value is ing the last 10 days of training under each linearlyrelatedtoreinforcersize(cf.Equation condition were taken as indifference delays, 1). The observed ratios were consistently ADJUSTING-DELAY SCHEDULE 65 Fig. 5. Resultsofthepowerspectrumanalysis.Comparisonofpowerinthedominantfrequencybandandperiodof oscillation correspondingto the dominantfrequencyseen under Conditions1 (open columns;reinforcersizes: q 5 A 25ml,q 5100ml)and2(shadedcolumns;reinforcersizes:q 514ml,q 525ml).Columnsshowgroupmeandata;open B A B circlesshowdatafromindividualrats.PowerwassignificantlyhigherunderCondition2thanunderCondition1(*p, .05);therewasnodifferencebetweentheperiodofoscillationunderthetwoconditions. smaller than 3.81, suggesting a nonlinear solution). Response rates in successive ratios relation between size and value. A nonlinear were analyzed using an equation derived from relation is assumed by the model of inter- Killeen’s (1994) ‘‘mathematical principles of temporalchoiceproposedbyHoetal.(1999), reinforcement’’. The ‘‘specific activation’’ whichformedthebasisofthemethodadopted parameter of Killeen’s model (a), which is heretoderivenumericalestimatesofdiscount- presumed to reflect the incentive value of the ing parameters. According to this model, reinforcer, was a monotonically increasing instantaneous reinforcer value is hyperbolical- function of reinforcer volume. A hyperbolic ly related to reinforcer size, the relation being function was fitted to the relation between a defined by a single free parameter, Q, which and reinforcer volume, from which it was specifies the reinforcer size corresponding to determined that the value of Q was 158.9 ml. the half-maximal value. Note that other Thefactthattheseradicallydifferentmethods nonlinear size/value functions have recently yielded numerical estimates of Q that were in beenproposed,forexample,byKilleen(2009) same order of magnitude inspires some and Pine et al. (2009). confidence in the general utility of this Thepresentexperimentemployedtwopairs parameter as a descriptor of sensitivity to of reinforcer sizes that allowed Q to be reinforcer size. determined from the ratio of the two indiffer- By substituting the estimates of Q into ence delays (Equation 4a). It is of interest to Equation 3, it was possible to derive estimates compare the value of Q obtained using this of the delay-discounting parameter, K. The tactic (mean 5 113.8 ml) with a value of Q mean value of K (0.082 s21) was similar to derived using a different approach. Rickard et values of this parameter obtained in previous al. (2009) trained rats under a progressive- experiments with rats (approximately 0.1 s21: ratioscheduleusingawiderangeofreinforcer Green, Myerson, Holt, Slevin, & Estle, 2004; sizes (different volumes of a 0.6 M sucrose Mazur, 2007; Mazur & Biondi, 2009). 66 L. VALENCIA TORRES et al. Methodological Considerations andanupperboundarydefinedbyq andq . B1 B2 If (d /d )/q 5 1/q , the recovered The derivation of Equation 4 entails the B(50)1 B(50)2 B1 B2 value of Q is ‘; higher d ratios yield simplifying assumption that when no delay is B(50) scheduled for Reinforcer A, d 5 0. In fact, a negative values of Q, which are, of course, A meaningless. The relation between Q and brief delay necessarily occurs between the d /d is illustrated in Figure 6B. Set- initiation of the reinforcer delivery and the B(50)1 B(50)2 tingq at100andq 525(thevaluesusedin subject’s consumption of the reinforcer. In- B1 B2 thepresentexperiment),meaningfulvaluesof formal observation of rats trained under the Q require d ratios , 4 (for q 5 50 the presentproceduresuggeststhatthisdelayisin B(50) B2 upper limit is , 2; for q 5 12.5, it is , 8). the order of half a second, and we therefore B2 thinkitunlikelythattheapproximationd 50 Withinasubstantialproportionoftherangeof A allowable ratios (approximately 1.5–3.5 in the significantlycompromisesthevalidityofEqua- present instance), the relation between log Q tion4.Moreover,thereisnomeasurabledelay and the d ratio is approximatelylinear. As between the response on Lever A and the B(50) showninFigure 6B,thedatafrom11ofthe12 presentation of exteroceptive stimuli associat- rats in this experiment fell within this band. ed with reinforcer delivery, which presumably The nature of the relation between the d acquire some conditioned reinforcing proper- B(50) ratio and Q dictates that small changes in the ties. size of the ratio will tend to produce larger It must be pointed out that the algebraic changesinQathigherratiosizesthanatlower substrateofthepresentmethodimposessome ratio sizes. This suggests that it may be restrictions on the range of reinforcer sizes appropriate for statistical tests on values of Q that may be employed. For example, in the present experiment we set q 5 q (25 ml) derived using the present method (for exam- B2 A1 and q 5 4.q (100 ml); the value of q ple in experiments examining the effect of B1 A1 A2 neurobiological interventions on this parame- required in order to preserve the equality (1/ q 2 1/q ) 5 (1/q 2 1/q ) was approx- ter) to be carried out on logarithmically A1 B1 A2 B2 transformed parameter values. imately 14 ml. Other reinforcer sizes might havebeenused,butthechoiceisnotlimitless. Itmustbeemphasizedthattheconstrainton For example, instead of determining the therangeofallowabledB(50)ratiosistheoretical required value of q for given values of q , rather than methodological. In other words, it A2 B1 q and q , the value of q might have been is not peculiar to the present application of A1 B2 A2 preselected, and the required value of q Equation 4; rather, it arises from the assump- B2 calculated accordingly. In this case, when q tions underlying Equations 2a and 2b, which B2 5q , thechosenvalueofq would havehad form the basis of Ho et al.’s (1999) multiplica- A1 A2 tobelessthanq /2,otherwiseanappropriate tive hyperbolic model. A more stringent con- B2 valueofq couldnothavebeenfound(e.g.,if straint is imposed by Equation 1, which does B1 q 5 25, and q 5 q 5 50, q 5 ‘). not incorporate a size-sensitivity parameter. A2 B2 A1 B1 Choosingconvenientvaluesofq ,q andq When applied to the present protocol, Equa- A1 B1 B2 and calculating the required value of qA2 tion1 specifiesadB(50)ratioofexactly3.81.As circumvents this limitation. Figure 6A shows discussed above, the present data do not therequiredvaluesofq forarangeofvalues comply with this specification. They are, how- A2 of q , when q is set at 100 and q is set at ever, compatible with the limits imposed by B2 B1 A1 12.5, 25 or 50; the points indicate the values Equation 4, and aretherefore compatiblewith corresponding to the particular condition the multiplicative hyperbolic model. It is used in the present experiment, in which q possible, of course, that future applications of A1 5 qB2. The figure shows that despite the thepresentmethodmayrevealempiricaldB(50) limitation outlined above, the method can in ratios that are incompatible with Equation 4; principle accommodate a broad range of such an occurrence would constitute a refuta- reinforcer sizes. tionoftheunderlyingmodel. The equations also impose constraints on Transitional Behavior on the Adjusting- the range of d ratios that can generate B(50) Delay Schedule meaningful values of the parameterQ.Inspec- tion of Equation 4a shows that the range of In agreement with previous reports (e.g. da allowable ratios has a lower boundary of 1.0 Costa Arau´jo et al., 2009; Mazur, 1987), the
