ERIC ED476148: Scoring Multiple True False Items: A Comparison of Summed Scores and Response Pattern Scores at Item and Test Levels.

42 Pages·2003·0.54 MB·English

by  ERIC

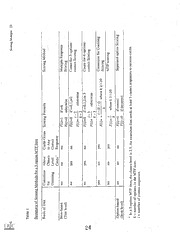
DOCUMENT RESUME
ED 476 148
TM 034 897
AUTHOR
Wu, Brad C.
Scoring Multiple True False Items: A Comparison of Summed
TITLE
Scores and Response Pattern Scores at Item and Test Levels.
2003-00-00
PUB DATE
NOTE
40p.
PUB TYPE Reports
Research (143)
EDRS Price MF01/PCO2 Plus Postage.
EDRS PRICE
*College Entrance Examinations; Foreign Countries; *High
DESCRIPTORS
School Students; High Schools; *Item Response Theory;
*Objective Tests; *Scoring
Additive Models; Taiwan
IDENTIFIERS
ABSTRACT
The additive and response patterns scoring methods within and
between multiple true-false (MTF) items were examined using data for 5,000
students for each of 2 years from the mathematics portion of the national
college entrance examination in Taiwan. For additive scoring at item level,
response to each option was scored dichotomously and added up to make an item
clustered score, while at test level response to each item was scored
dichotomously or polytomously by applying four methods, and then adding to
sum of item score. For response patterns scoring the item response theory
(IRT) ability estimated were estimated through the expected a posteriori
procedure. The within-item IRT ability estimates were compared to the sum of
the item scores at test level. Correlations between item clustered scores and
within-item ability estimates were significant for all 10 items examined;
correlations between sum of item scores and between-item ability estimates
were also significant for all four scoring methods in two sets of tests. The
results suggest that even at the risk of losing information, the use of item
clustered scores and sum of item scores as estimates of the latent trait is
reasonable, although the appropriateness of the item clustered scores should
be examined prior to the test level estimation. The IRT ability estimates can
be more informative when variation of discrimination parameters within items
is large. The influence of item parameters on the IRT ability estimates was
also discussed. (Contains 2 figures,
7 tables, and 39 references.)
(Author/SLD)
Reproductions supplied by EDRS are the best that can be made
from the original document.
Scoring Multiple
ITEMS: A COMPARISON OF
Running Head: SCORING MULTIPLE TRUE FALSE
of Summed Scores and Response
Scoring Multiple True False Items: A Comparison
Pattern Scores at Item and Test Levels
Brad C. Wu
University of Washington
PERMISSION TO REPRODUCE AND
U.S. DEPARTMENT OF EDUCATION
Ofliie of Educational Research and Improvement
DISSEMINATE THIS MATERIAL HAS
EDUCATIONAL RESOURCES INFORMATION
BEEN GRANTED BY
CENTER (ERIC)
B. Ching-Chao Wu
This document has been reproduced as
received from the person or organization
originating it.
Minor changes have been made to
improve reproduction quality.
TO THE EDUCATIONAL RESOURCES
INFORMATION CENTER (ERIC)
Points of view or opinions stated in this
document do not necessarily represent
1
official OERI position or policy.
BEST COPY AVAILABLE
Scoring Multiple
2
Abstract
within and between, multiple
The additive and response patterns scoring methods
scoring at item level, response to
true-false (MTF) items were examined. For additive
item clustered score, while at
each option was scored dichotomously and added up to an
either dichotomously or polytomously
test level response to each item was scored
For response patterns scoring
applying four methods and added up to a sum of item score.
Expected a posteriori procedure. The
the IRT ability estimates were estimated through
the clustered scores at item level and
within-item IRT ability estimates were compared to
compared to the sum of item scores at test
the between-item IRT ability estimates were
and within-item ability estimates were
level. Correlations between item clustered scores
between sum of item scores and
significant for all 10 items examined; correlations
for all four scoring methods in two
between-item ability estimates were also significant
item
the risk of losing information, the use of
sets of test. The results suggest even at
of the latent trait is reasonable. But
clustered scores and sum of item scores as estimates
should be examined prior to the test level
the appropriateness of the item clustered scores
informative when variation of
estimation. The IRT ability estimates can be more
influence of the item parameters on
discrimination parameters within items is large. The
the IRT ability estimates was also discussed.
Scoring Multiple
3
of Sum Scores and Response Pattern
Scoring Multiple True False Items: A Comparison
Scores at Item and Test Levels
reliability than the other item
Despite many superior qualities such as higher
1979; Albanese and Sabers, 1988;
formats (Hills and Woods, 1978; Albanese et al,
1982; Kreiter and Frisbie, 1989) and more
Mendelson et al, 1980; Frisbie and Sweeney,
the
given time multiple-true-false (MTF) items possess,
responses collected in a
Multiple-Choice (MC) item has been limited.
application of this alternate format of the
attributed to the ambiguous status that
The major reason of its rarity can partly be
the MC
interpretation of the scores. Similar to
complicates the scoring procedure and
difference is
question stem and a few options. The
item, a typical MTF item consists of a
asked to judge each option following the
that in responding to MTF items, examinees are
only one correct option as required in
question stem as true or false instead of selecting
either be an option or an item. In other
MC items. Under such format, the scoring unit can
for the item as a whole or response to
words, the collection of responses can be scored
possible to
dual scoring options also make it
each option can be scored separately. The
option in the MTF item
dichotomously or polytomously. While each
score MTF items
the
(TF) item, the content congruency among
takes a form of an individual True False
Context
MTF item close to the format of
options following each stem also brings the
subset, or a
in an item are constructed as a
Dependent Item Set (CDIS), in which options
1990).
testlet (Wainer & Kiely, 1987; Wainer & Lewis,
individual TF items, and scored
When all the options are treated independently, as
could seriously increase the
dichotomously, guessing factor and local item dependency
preferred because the sum
the latent trait. Clustered scoring is thus
error in estimating
Scoring Multiple
4
clustered score to
efficiently incorporated into one
scores of within item TF responses are
change helps to reduce the error due
provide estimates of performance at item level. This
general solution to the problem of local
to the probability of guessing and serves as a
clustered score for each item
dependency (Yen, 1993). However, the efficacy of one
different response patterns. For
ignores the fact that a given score can result from
of 3 could be a result of
example, for an MTF item with 5 options, a clustered score
trait due to
reflect a different degree of the latent
response patterns. Each pattern may
Examinees who have same numbers of correct
the varied characteristics of the options.
have different degrees of latent trait due
option but.have different response patterns may
and discrimination of the options. Similarly, examinees
to the distinguished difficulty
different response patterns among items
could earn the same total score on a test based on
examinees with a score of 10 could demonstrate
ci2o°
on the test. For a 20-item test,
whether to use sum of raw scores or response pattern
response patterns. The question of
been intensively
testlets, or tests combing different formats have
scores in MC items,
items.
discussed in the past, but rarely in relation to MTF
Sum of raw scores
been used to estimate ability.
In scoring MTF items, raw scores have always
made to yield different MTF
Various linear arrangements on the raw scores can be
based on raw
Albanese and Sabers (1988), different scoring methods
scores. In a study by
each option
examined for item and reliability analyses. When
scores of MTF items were
true-false unit, dichotomous scoring
of the MTF item was treated as an independent
1 and incorrect response to an
applied to correct response to an option was scored as
several options was treated as a unit,
option was scored as 0. When each MTF item with
Scoring Multiple
5
polytomously applying different
each item could be scored either dichotomously or
for an item of several options
scoring methods. For example, they used a clustered score
Also, when only some of the options in an
instead of dichotomous scores for each option.
given. These methods were developed
item were responded correctly, partial-credit was
correction-for-
dependency and guessing. Other methods such as
to compensate for local
below chance level. The partial credit
guessing was applied to discredit correct responses
larger than chance level (half of
approach assigned credit only to total correct responses
approach subtracted credit as penalty
the total options), and the correction-for-guessing
of these scoring methods led to the
for the incorrect responses. The combinations
the count-for-2-options-correct
development of a) the multiple-response scoring, b)
d) the correction-for-guessing scoring,
scoring, c) the count-for-3-options-correct scoring,
separated-option scoring (Albanese and
e) the credit-for-any-correct scoring, and f) the
Lorscheider, 1980; Sanderson, 1973).
Sabers, 1988; Gross, 1978; Harasym, Norris, and
does nothing but reduce the raw
Research suggests that correction for guessing
1989; Tsai and
difficult (Hsu, Moss, and Khampalikit,
score to make the test seem more
the
credit to partially correct responses, on
Suen, 1993). The approach of giving partial
higher test score reliability when compared
other hand, yields a higher raw score and also
(Albanese,
method such as the multiple-response scoring
to a dichotomous scoring
The MFT scoring methods discussed
Sabers, 1988; Hsu, Moss, and Khampalikit, 1989).
thus far are summarized in table 1.
Insert Table 1 Here
Scoring Multiple
6
Response pattern scores
in MC items and CR items but
Response pattern scoring has been applied mostly
using raw scores, response pattern scoring
not in MTF items. Unlike the scoring methods
of various weighting schemes.
has usually been conducted with the application
shown that the aim of achieving
Comparisons of implicit and explicit weighting have
estimates of latent trait can be met by both. However,
more detailed and reliable
validity (Rudner, 2001), therefore,
maximizing reliability by weighting may lead to lower
contributions and the trade-offs
weighting should be a rational process evaluating
(Hennedy and Walstad, 1997).
procedure, which simultaneously
Among the weighting schemes is the IRT
ability based on the item parameters.
calibrates all test items and estimates examinees'
ability estimation implicitly weighs each item
The consideration of the item parameters in
IRT scaled score for each examinee.
(or option within an MTF item) and provides an
each response pattern is usually estimated
Under the IRT scheme, ability associated with
the Expected a posteriori (EAP) method.
by the Maximum a posteriori (MAP) method or
derived from the product of corresponding
For the MAP, the mode of the joint likelihood
is
distribution is calculated. For the EAP, the mean
trace lines and the N(0,1) population
associated with a sum can be attributed
used. The variation of the MAP or EAP estimates
derived from
IRT models selected. IRT ability estimates
to the variable parameters in the
because
equivalent to summing the item scores
one-parameter logistic (Rasch) model are
assumed. IRT ability estimates
identical slope parameter and 0 guessing parameter are
influenced by the item location
derived from the two-parameter logistic model are
For estimation based on the three-
(difficulty) and the slop (discrimination) parameters.
Scoring Multiple
C
discrimination parameters affect the ability
parameter logistic model, item location and
discriminative items will have
estimate (Lord, 1980, pp. 74-77). In other words, more
items.
larger weights than less discriminative
lead to more detailed and
While weighted scoring based on response patterns may
generally been used in scoring MC
reliable estimation of latent trait, raw scores have
item formats. Besides the reason that raw
items, CR items, testlets, and tests of combined
difference in ability
convenient, Thissen (2001) argued that the
scores are simple and
of
sum of raw scores is minor. The range
estimates resulting from IRT scaled scores and
because of a strong linear relationship
scaled scores around the sum scores is small
for tests consisted of both MC and
between IRT scaled scores and the sum of raw scores
CR items.
ability estimates and the sum of raw
For MTF items, the relationship of the. IRT
level, the clustered
examined at both item and test levels. At the test
scores should be
is associated with
add up to a total test score. Each total score
scores of all MTF items
IRT ability estimates. The
various item response patterns and their corresponding
by the parameters of each MTF item.
variation of these ability estimates is determined
and the total raw scores at the test level,
Comparison of the IRT generated scaled scores
of clustered scores in representing item
however; relies on the appropriateness of the use
require judgments on several options and
performance. Unlike MC items, MTF items
items should likewise be examined and
thus the patterns of judgment within MFT
compared to the corresponding clustered score.
The research questions of the study are:
Scoring Multiple
8
between sum of raw scores and
1. Does the same type of linear relationship exist
in MTF items as in MC and CR
IRT ability estimates based on response patterns
items?
MTF item rather than separate
2. Is it appropriate to use clustered scores for an
item? Also, is it appropriate to use sum of
scores for each option within an MTF
to estimate
item raw scores rather than weighted item response pattern scores
latent trait?
relationship between the raw scores
The purpose of this study is to examine the
the use of item clustered scores and
and the response pattern scores in MTF items, and
examining
estimates of latent traits. This is done by first
sum of item scores as
pattern scores within
relationship between IRT ability estimates derived from response
from
then between the ability estimates derived
MTF items and item clustered scores,
stepwise.
different scoring methods and the sum of item scores
Method
Instrument and Data
from the Group I Mathematics
The data examined in this study are the MTF items
Examination (NCFF) held in Taiwan on July 2,
test of the National College Entrance
for examinees who aim at
2000 and July 2, 2001. The Group I mathematics is the test
Humanistic Science, and thus the
majoring in Social Science, Art, Business, and other
knowledge and skills quite different from the
test places emphasis on mathematical
those planning to major in the Natural
Group II Mathematics test which is designed for
graduates took the Group I
Sciences. A total of 85,614 and 86,314 high school
each year, 5,000 examinees were
Mathematics test in 2000 and 2001 respectively. For
Scorifig Multiple.
9
examinees were eliminated from analysis
randomly selected from the population. Sample
left unanswered. The data screening
and ability estimation if any of the MTF item was
for year 2000 and 2001 respectively.
resulted in sample examinees of 3,960 and 3,831
is similar to 25 TF items clustered
Each MTF item is followed by5 options. This
(see Appendixes A and B) cover the
into 5 testlets. The five MTF items for each year
10th to 12th grade, which
Mathematics curriculum from
content in the standard Group I
Statistics. A difference from the traditional
includes Algebra, Geometry, Probability, and
following the
indicated that at least one option
MTF item is that the directions for the test
the
Multiple Answer (MA) format where
item stem is true. This is sometimes called the
2k -1 (k is number of options). In a 5-
number of possible response patterns becomes
the number of response patterns is then
option MTF item with at least one correct option,
items
The examinees' response patterns to all 5
31 because "all false" pattern is excluded.
analysis.
were collected for the
Insert Appendix A and Appendix B Here
Item Scoring
compared. The first method was to
Each MTF item was scored twice and then
(for correct response).
dichotomously as 0 (for incorrect response) or 1
score each option
item cluster score that ranges from 0 to
5.
The five option scores were added to create an
method
of raw option scores. The second
The item cluster score was mere summation
the response
in which item score was estimated based on
was the IRT ability estimate,
method, the parameter estimations
pattern to the five options. Prior to choosing the IRT
using
item. Model fitness was estimated
and item fit statistics were 'performed for each
10