DTIC ADA527190: Numerical Simulations of Mountain Waves in the Middle Atmosphere over the Southern Andes

9 Pages·1.7 MB·English

by  Defense Technical Information Center

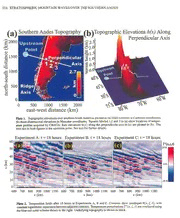
Numerical Simulations of Mountain Waves
in the Middle Atmosphere over the Southern Andes
Kwok-Aun Tan
Schoof of Mmhemalics.Unil.ersiryofNewSouthWales.Syd.ley.Allslralia
Stephen D. Eckermann
E. O. Hulburt Center for Spoco!' Research. Naval Research lAborolOry. Washington. DC
We use a two-dimensional nonlinear compressible mesoscale model to study
mountain waves in the middle atmosphere over the southern Andes. Using re
alistic temperatures, winds and topography, the model generates large-amplitude
long-wavelength breaking mountain waves in the middle atmosphere that compare
favorably with satellite measurements. Modeled waves have preferred horizontal
wavelengths. Spectral analysis reveals correspondences between these wavelengths
and peaks in the spectrum of Andean topographic elevations. The shorter waves
reach (he stratosphere weJl before (he longer ones, consistent with group veloc·
ity arguments. with longer wavelengths ultimately dominating. At later times we
find evidence of downward propagating secondary waves produced by upper.level
breaking of the primary waves.
I. INTRODUCTION linear nonhydrostatic mountain wave solutions within real
istic wind profiles from the ground up to -70-80 km. More
Theory and parameterization have indicated that gravity detailed numerical simulations were performed by Bacmeis
waves forced by flow over mountains are a major source terand ScJweber/ [1989] using a two-dimensional nonlinear
of dynamical driving for the stratosphere and mesosphere time-dependent anelastic model of flow over an obstacle.
[e.g., Bacmeisler, 1993; Bovifle. 1995J. Detailed mesoscale They found zones of strong wave overturning in the middle
model simulalions have proved useful in modeling mountain atmosphere that generated secondary down ward-propagating
wave dynamics and refining simpler parameterizations of waves. Their model used idealized representations of the
these processes in the troposphere and lower stratosphere background atmosphere. Satomura and Sato 11999] used a
[e.g., Laprise. 1993; Kim and Arakawa, 1995; D!uran, 1995; fully nonlinear compressible two-dimensional model of Row
Broad. 1996; Diirnbrack et al., 1998]. over orography with realistic representations of the lower
However, only a few such models have incorporated a and middle atmospheres, based on climatology. They too
middle atmosphere and investigated mountain wave dynam simulated strong wave breaking in the middle stratosphere
ics up to and beyond the stratopause. One of the first rela and generation of secondary waves from these unstable re
tively detailed studies was by Sclweberl (1985], who derived gions. although the wavelengths differed from those found by
Bacmeister and Schoeberl [1989]. All of these studies con
sidered flow over a bell-shaped obstacle and omitted Coriolis
accelerations.
Here, we lake further Sleps towards "real world" mesoscale
Atmospheric Science Aeross the Stratopause
model simulations of mountain waves in the middle atmo
Geophysical Monogntph 12]
sphere. Our simulations focus on a specific set of satellite
Copyright 2000 by the American Geophysical Union
311
Report Documentation Page Form Approved
OMB No. 0704-0188
Public reporting burden for the collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources, gathering and
maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information,
including suggestions for reducing this burden, to Washington Headquarters Services, Directorate for Information Operations and Reports, 1215 Jefferson Davis Highway, Suite 1204, Arlington
VA 22202-4302. Respondents should be aware that notwithstanding any other provision of law, no person shall be subject to a penalty for failing to comply with a collection of information if it

does not display a currently valid OMB control number.
1. REPORT DATE 3. DATES COVERED
2000 2. REPORT TYPE 00-00-2000 to 00-00-2000
4. TITLE AND SUBTITLE 5a. CONTRACT NUMBER
Numerical Simulations of Mountain Waves in the Middle Atmosphere
5b. GRANT NUMBER
over the Southern Andes
5c. PROGRAM ELEMENT NUMBER
6. AUTHOR(S) 5d. PROJECT NUMBER
5e. TASK NUMBER
5f. WORK UNIT NUMBER
7. PERFORMING ORGANIZATION NAME(S) AND ADDRESS(ES) 8. PERFORMING ORGANIZATION
Naval Research Laboratory,E.O. Hulburt Center for Space REPORT NUMBER
Research,Washington,DC,20375
9. SPONSORING/MONITORING AGENCY NAME(S) AND ADDRESS(ES) 10. SPONSOR/MONITOR’S ACRONYM(S)
11. SPONSOR/MONITOR’S REPORT
NUMBER(S)
12. DISTRIBUTION/AVAILABILITY STATEMENT
Approved for public release; distribution unlimited
13. SUPPLEMENTARY NOTES
14. ABSTRACT

15. SUBJECT TERMS
16. SECURITY CLASSIFICATION OF: 17. LIMITATION OF 18. NUMBER 19a. NAME OF
ABSTRACT OF PAGES RESPONSIBLE PERSON
a. REPORT b. ABSTRACT c. THIS PAGE Same as 8
unclassified unclassified unclassified Report (SAR)
Standard Form 298 (Rev. 8-98)
Prescribed by ANSI Std Z39-18
312 STRAT OSPHERJC MOUNTAIN WAVES OVER THE SOUTHERN ANDES
measurements of mountain waves over the region shown in 3. NUMERICAL MODEL AND DOMAIN
Plate la. Colored squares, labeled 1,2 and 3. show locations
3./. Model Description
of three successive vertical temperature profiles acquired by
the Cryogenic Infrared Spectrometers and Telescopes for the The model used here was developed from an earlier version
Atmosphere (CRISTA) on 6 November, 1994 at 6:24 lff. first described by Tan and Leslie (1998J. It solves the Eu
These profiles, reproduced in Plate 4 of Grossmall (2000]. ler equations for fully compressible nonlinear nonhydrostalic
reveal coherent stratospheric temperature oscillations. Eck atmospheric How over arbitrary terrain in a two-dimensional
emwnn alld Preusse (1999) used theory and parameteriza spatial domain. The velocity u = (u, v, w), potential tem
tion to argue that these oscillations were large-scale mountain perature 0 and Exner pressure "/I" are split into background
waves generated by How over the Andes. and perturbation tenns, as follows:
In section 2. we show that two-dimensional mesoscale
model simulations offer a potentially useful means of study u(z,z,t) ii(z) + u'(z, z,t),
ing the generation and evolution of the mountain waves ob 8(z",t) 8(,) + 8'«" ,t),
served on this day. We describe our mesoscale model in 1I"(z,z,t) = i(z) + "/I"'(z, Z, t).
section 3, and apply it in section 4 using "best" estimates
of the large-scale winds, temperatures and orography. The The velocity components v and w contain perturbation terms
results are analyzed in section 5 and the findings are summa only. A background temperature profile 1'(z) is used to
rized in section 6. initialize the background density ,o(z), potential temper
aure 8(z) and Exner pressure i(z) = T(z)/8(z), assuming
2. CRISTA OBSERVATIONS AND REGIONAL hydrostatic equilibrium. The cross-ridge background How,
DOMAIN ii(z), is assumed to be in thennal wind balance. The m0-
mentum, thennodynamic and continuity equations become:
Plate I shows that the large-scale topography here is quasi
two dimensional. The "ridge axis" in Plate 1a is a subjective
fit to the orientation of the long axis of the Andes. The "per
du' 8u 87r'
pendicular axis," aligned normal to this ridge axis, passes as -+w'-+,8--fv' = D(u'), (\a)
close as possible to the three CRISTA profiles, and illustrates dt 8z p 8x
that the CRISTA data were acquired along an orbital segment -dv+' uf' = D(v'), (\b)
dt
that passed nearly orthogonally across the ridge axis of the
Andes. -dw+' ,o8-"/1-"' g_8' = D(w'), (\,)
We take the blue dot in Plate I at the westem end of the dt p 8:: 8
perpendicular axis as our "upstream point," since surface d8' ,89
-+w- D(8'), (\d)
winds were eastward and the atmosphere here is far enough dt 8,
upstream to remain unaffected by the Andes [Seluchi et al. .
1998). Figure I a plots a hodograph of the horizontal wind dd7rt' + w ,88:i: + c~p8 2 V . (p8u') = 0, (\e)
profile at the upstream point on 6 November. 1994 at 6:00 UT, p
using data from NASA's Data Assimilation Offiee [Coy and
Swillballk, 1997]. Upstream troposphere-stratosphere winds where
were roughly parallel to the perpendicular axis at this time.
( 8(;;8u') 8(pBW'))
particularly near the surface and in the stratosphere, our pri 'V . (pBu') -
8x + 8:: '
mary regions of interest. Maximum deviations of _450 oc
curred near the tropopause in Figure 1a. d a (_ ') a ,8
= &t. + u+u 8x +w 8::'
Similar conditions occur when eastward surface winds dt
How in from the ocean across the Norwegian Mountains.
In these situations, three-dimensional mesoscale models of
ten predict long two-dimensional (plane) mountain waves c and c" are the mass specific heats at constant pressure and
p
in the lower stratosphere over Scandinavia, which compare volume, respectively, R = cp - c" is the gas constant for
well with aircraft and radiosonde data [Leutbecller and Volk dry air. 9 is the gravitational acceleration, c, is the speed of
ert, 1996: Dombrack et aI., 1998, 1999]. Consequently. sound and f is the Coriolis parameter. The D(X') terms
these waves can be modeled fairly accurately using a two in (la}-{Id) are damping terms for the perturbation quanti
dimensional mesoscale model [Volkert and fnrts, 1992J. We ties X', and represent the combined effeclS of a first-order
too use a two-dimensional mesoscale model as a first step in turbulence closure scheme [Lilly, 1962], fourth-ordercompu
this study. talional damping (to suppress small-scale numerical modes),
TAN AND ECKERMANN 313
cause numerical aliasing. In all experiments. wind profiles
were ramped up over 2 hours from an initia1 state of rest, to
minimize the generation of transient oscillations [e.g.,lkllwa.
19901. The upper-level sponge was effective above ...... 55 km.
Equations were forwarded using 6J./ = 5 sand 6J., = I s.
4. MODEL SIMULATIONS
4.1. ExperimefltsA. Ballde
Figure I. (a) Hodograph of horizontal winds over the upstream Three different model experiments, denoted A, B and C,
point in Figure I. taken from DAO assimilated data on 6 November. were conducted. As shown in Figures Ib and Ic, each
1994. 6:00 lIT. The altitudes (in kilometers) of each wind value successive experiment more closely approximated the up
are labeled along the hodograph trace. Orientation of the perpen
stream DAO wind and temperature profiles at the time of the
dicular axis in Plate 1a is shown with a broken line; (b) black
CRISTA measurements.
solid curve shows the upstream DAO winds along the perpendic
ular axis. u(:). Other labeled curves show model ii(:) profiles Experiment A used an idealized wind profile u(z) that
used in Experiments A. 8 and C; (c) vertical profile of upstream omitted the westward shear layer in the DAO profile above
DAO temperatures (solid black curve). and the model curves used 35 km (Figure Ib). This control experiment allowed us to
in Experiments A. 8 and C. study mountain wave generation and propagation without the
complication of critica1-level effects (u(z) = 0).
and a sponge layer (Rayleigh damping) at upper levels [Dur
In Experiment B, a linear westward shear layer was intro
ran and Klemp, 1983].
duced above 35 km, yielding u(z) = 0 at z ~ 43 km. Experi
To incorporate topography at (he bouom boundary, the
ment B allowed us to introduce the critical layer. while main
model uses the terrain-following vertical coordinate
taining an identical atmospheric situation to Experiment A
below 35 km. To this end, both experiments used background
L [, - h(.)]
temperatures 1'( z) from the 1976 U.S. Standard Atmosphere
(.,,)= L-h(. ) , (2)
at mid-latitudes [MinZfler, 1977]. which fit the upstream DAO
temperatures from ....... 0-55 km quite well (Figure Ic).
where L is the top model altitude and h(:t) is the topographic Experiment C used cubic spline fits to the DAO wind and
height function [Gal-Chen and Sommerville, 1975J. A free temperature profiles from 0-55 Jun. This yielded a zero wind
slip lower boundary condition is used. line at z ~ 46 Jun, slightly higher than in Experiment B.
The model equations (laHle) are solved numerically Lacking DAO data above 55 km. from 55-80 km we used
using the Klemp-Wilhelmson time-splitting method on an constant winds and a linear temperature gradient equal to
Arakawa C-grid [Klemp and Wilhelmson, 1978; Durran and that in Experiments A and B.
Klemp, 1983; Wicker and Skomarock, 19981. The second
order Runge-Kuua method is used for the large time steps. 4.2. Results
6.t/, and the forward-backward scheme is used for the small In all three experiments, mountain waves entered the mid
time steps. 6J.,. An implicit method is used in the verti
dle atmosphere after a few hours and produced overturning
cal for the acoustic tenns in the governing equations. A
isentropes after ....... 6 hours. We focus on temperatures since
third-order upwind finite difference scheme is used for the
CRISTA measured temperature perturbations. Plate 2 plots
advection terms and second-order centered finite differenc potential temperatures 8(x,(,t) and temperature perturba
ing is used for the pressure gradient and divergence tenns. tions T'(x, (, t) after t = 18 hours over the orographic region
The Miller-Thorpe radiation condition is used at the lateral
in each experiment. The critica1levels in Experiments B and
boundaries to prevent side reflections [Miller and Thorpe,
C efficiently absorb mountain waves, and yield rapid wave
19811. The current model configuration was validated by
shortening and intense breaking at closely underlying alti
reproducing mountain wave patterns from previous two
tudes. Despite the different wind profiles and the significant
dimensional model experiments (e.g .• Doyle et al.. 2000J.
amounts of overturning and mixing by this time, the large
scale wave structures below 35 km are quite similar in each
3.2. Model Domain and Initialization
experiment.
The perpendicular axis:t in Plate 1 extended to 3000 km The wave fields evolve significantly with time. as illus
in our model with a grid resolution 6.z = 2 km. We set the trated in Figure 2 using results from Experiment C. The
model lid L = SO km and vertical resolution 6.z = 0.5 km. middle atmosphere is dominated initially by short horizontal
Topographic elevations h (:t) in Plate I b were smoothed to wavelengths, which trigger vigorous overturning and mixing
remove the two and four grid-point wavelengths that can by 8 hours. The turbulent zones persist and seem to move
314 STRATOSPHERIC MOUNTAIN WAVES OVER THE SOUTHERN ANDES
(a)
Southern Andes Topography ) Topographic Elevations h(x) Along
EOOO Perpendicular Axis
<I)
g
1500
~
:'a"
-
..d 1000
'"
o
,
'"
' €
g
500 1000 1500 2000
east-west distance (lan)
Plate 1. Topognphic elevations over southern South America. ploued as (a) filled contours in Canesian coordinates.
(b) three-dimensional elevations in Mercator coordinates. Squares labeled 1,2 and 3 in (a) show locations of temper
ature profiles acquired by CRISTA. Raw elevations h( x) along the perpendicular axis in (a) are ploned in (b). The
blue dot in both figures is the upstream point. See text for further details.
600 700 gOO 900 1000 1100 600 700 800 900 1000 1100 600 700 800 900 1000 11 00
x (Ion) x (Ion) x (Ion)
Plate 2. Tempenlture fields after 18 hours in Experiments A. Band C. Contours show isenuopes 8(z,("t). with
constant logarithmic separation between adjacent contours. Tempenlture perturbations T(x, (" t) are overlayed using
the blue-red color scheme shown to the right. Underlying topography is shown in black.
TAN AND ECKERMANN 31S
600 700 800 900 1000 1100 600 100 800 900 1000 1100 600 700 800 900 1000 1100 600 700 800 900 1000 1100 600 700 800 900 1000 1100
.. (km) • (km) .. (bII) .. (bn) .. (km)
Figure 2. lsentropes 9(z, (, t) from Experimenl C afler t = 6, 8, 10, 15 and 24 hours. Same constant logarithmic
separation between contours is used in each panel. Underlying topography is shaded.
downstream after 10 hours. Thereafter, progessively longer 5.2. 1i~ Evolution
horizonlal wavelengths come to dominate the wave field, and
Figures 2 and 3 show that the dominant horizonlal wave
less vigorous overturning is evident. After 24 hours, waves
lengths change with time. Short~.z: values dominate the mid
at lower stratospheric levels are suppressed compared to their
dle atmosphere initially, giving way to progressively longer
earlier intensities.
horizontal wavelengths at later times. The vertical group
velocity of any hydrostatic wave ().;! ~i <: 1) is given by
5. ANALYSIS
IJw '\;N(,)
5.1. Wavelength Selection = =
cgz {)m 2lf~.z: . (4)
Preferred vertical wavelengths are evident in Plate 2 and
Figure 2. The vertical wavelength of a slationary hydrostatic From (3), all waves below 35 km have similar vertical wave
mountain wave is given theoretically by lengths ~z, and so the vertical group velocities of various
,\ ( ) _ 2,.(,) .'r-,';'- '''It.t'-''~ ... ,',-I'!'~!!t;;;~~i!=!!l
• z -.. N(z) , (3) T,('i;':il i'l IIJ
I "I"""
where N is Brunt-Vaisala frequency and lI' has its usual
meaning here. At 1$-30 kin, u(z) = 20 m S-I and
N = 0.021 rad S-I, which yields ~. = 6 km, in agreement
with the dominant vertical wavelengths found below 35 km
in all three experiments. In Experiments Band C, where
westward shear was introduced above 35 km, ~. decreases
with height in accordance with (3).
Preferred horizonlal wavelengths~.z: also emerged in each
experiment (Figure 2). We studied this spectrally by re
gridding T'(z,(, t) fields onto a regular height grid z, then
computing two-dimensional power spectra Fr(K, M) over
the range x = 250-1250 km and Z = 12-32 km. As ex
pected from (3), for all K a sharp spectral peak occurred
at a vertical wavenumber lA"711:::: 211'(6 km)-', enabling us to
study overall spectral variability in these simulations using
the one-dimensional spectral slice Fr(K, M ~ AI).
Spectra from each experiment are plotted in Figure 3 after
6, 15 and 24 hours. The power spectrum of the topogra Figure 3. One-dimensional sections of the two-dimensional power
phy hex) is plotted in Figure 3d, with evident peaks marked spectra FT(K, AI) at AI = At = 116 cyc km-I from Experiments
by light solid lines. These same lines are also ploued in the A, 8 and C after (a) 6 hours, (b) 15 hours, and (c) 24 hours.
Spectra were computed from T'(z, z, t) fields in the region z = 12-
other panels of Figure 3, and show that peaks in stratospheric
32 kin and:r; =250-1250 km. Since AI straddles the third and
temperature spectra correspond quite well with peaks in the
founh hannonics of these spectra, we plot averages of the slices at
topographic spectrum. Thus, horizontal wavelength selec·
these two hannonics. Panel (d) plots power spectral density of the
tion seems to be governed by spectral features in the Andean topographic elevation hex). Local maxima in (d) are highlighled
topography. with gray venicallines, and are also shown in the preceding panels.
316 STRATOSPHERIC MOUNTA IN WAVES OVER THE SOUTHERN ANDES
mountain wave modes are inversely proportional to their hor spectral density appeared in each ex.periment. most promi
izontal wavelengths. )...,. nently at long horizontal wavelengths. Vertical velocity spec
Using (3) and (4). a wave of )..., = 50 km has a group tra FT(l<, M) also showed downward propagating variance
velocity c~. ~ 2.5 m S-I. and thus takes -3.5 hours to at shorter horizontal scales. The appearance of these features
propagate to z = 30 km. Spectra in Figure 3a confirm in Experiment A indicates that this is not a critical-level reo
that the peak near )..., = 50 km is fully developed after 6 Hection effect, as expected since mean Richardson numbers
hours. Conversely. a)..., = 150 km wave takes -10 hours to are too large [Jones. 1968). Rather, these findings are in qual
propagate to 30 km. Stratospheric mountain wave energy at itative agreement with previous simulations of secondary
this scale does not develop fully until-IO-l5 hours into the wave generation by mountain wave breaking [Bacmeister
simulation (Figure 3b). Note that u(z) was ramped up from alld Schoeberl, 1989; Satomura and Sato. 1999).
zero during the first two hours, and was <20 m S-1 below Bacmeisler and Schoeberl (1989) found that their down
17 km. making actual propagation times somewhat longer. ward propagating secondary waves eventually led to reduc·
The mean width of the topography h(.:t) is ...... 300-500 km tions in overall wave intensity well below the regions of wave
(see Plate I). which might be expected to force a).r - 300- breaking. Attenuated wave activity at lower levels also arose
500 km wave most strongly. Indeed, ridge widths here are in our simulations (Figure 2e). Whether the attenuation noted
similar to those in northern Scandinavia, where very long here results mostly from the effects of downward propagating
mountain waves often dominate the stratospheric wave field secondary waves, or from breakdown of and additional tur·
[Dombrock el 01., 1998, 1999]. Using (3) and (4), after bulent damping by progressively longer upward-propagating
24 hours a 400 km wave would have propagated to a height primary waves, is unclear at present.
of only 20 kmor so, and thus would not be fully developed in
the middle atmosphere. Spectra after 24 hours confirm this: 5.4. Comparison with CRISTA Profiles
while Ex.periments A and B show a peak at a wavelength
The general form of the profiles over the Andes compares
-400·500 km in Figure 3c. spectra from Ex.periment C peak
favorably with the CRISTA data. Figure 4 plots a sam·
most strongly nearer 200·250 km. Thus. longer simulations
pIe temperature perturbation profile from fuperiment C at
are needed to assess whether a)..., -400 km wave eventually .:t = 845 km, a location between points I and 3 in Plate
dominates the middle atmospheric wave fluctuations [see
la. The CRISTA profiles at these points are overlayed [see
also Dombrock et 01., 1999).
Plate 4 of Grossmann. 2000]. The wavelength. amplitude
Once each spectral peak has developed in Figure 3, its
and general height variation of the model profile are all quite
intensity tends to wane thereafter. due to wave breaking and
similar to the data. Oscillations in Ex.periment C seem to
increasing turbulent damping. As longer waves subsequently
penetrate slightly higher prior to shortening and dissipating
enter the region and break, the additional turbulence and
below the critical layer. Note too that the amplitudes of the
interactions they engender probably act to damp these shorter
CRISTA profiles are probably underestimated due to instru·
horizontal wavelengths further.
mental effects. and that CRISTA cannot resolve any waves
of),. ,:5. 3-5 km {Eckennann and Prr!usse. I999J.
5.3. Downward Feedback
Model profiles from locations directly over points I and
AlthoughExperiments A and B used identical background 3 are not in phase with the CRISTA perturbations. This
atmospheres below 35 km, the results in Plates 23 and 2b is due to somewhat different horizontal wavelengths in the
after 18 hours are identical only below -20 km, and show model simulations. Eckenllann and Prr!usse [1999J showed
significant differences above -25 km. The time evolution that the oscillations measured by CRISTA had a horizontal
of these differences can be gleaned from Figure 3. After wavelength of either 400 km or 400/3 ~ 130 km. Peaks
6 hours the spectra in Experiments A and 8 are identical, but somewhat near these values appear in Figure 3c. although
show differences after 15 hours. 8y24 hours (Figure 3c), the other peaks also occur and there are variations among the
differences are as large in places as those from Ex.periment C. experiments.
These differences become evident below 35 km after
waves start breaking. Implicit numerical diffusion in this
6. SUMMARY AND DISCUSSION
model is very small, so these differences must originate from
downward feedback of differing dynamics originatingabove We have developed a high·resolution high~altitudenonlin­
35 km, where different u(z) profiles yield different wave and ear numerical model of compressible atmospheric flow over
turbulence fields. Turbulence itself cannot be advccted this arbitrary topography, and have used it here to simulate moun
far downwards, since we include no mean vertical wind. tain waves in the middle atmosphereoverthe southern Andes.
Two-dimensional spectra FT(K, M) separate upward and The results have confirmed that stratospheric temperature
downward propagating waves [e.g., Bacmeister and Schoe perturbations measured by CRISTA on 6 November, 1994
berl, 1989]: only the upward components are ploued in Fig were produced by intense breaking mountain waves forced
ure 3. After 12-24 hours, significant downward~propagatjng by flow over the southern Andes, as argued by Eckemlanll
TAN AND ECKERMANN 317
Wlr---~----'-~~~~-c 1998]. While two-dimensional models with turbulence pa
_CRIS'Aprllllle~ -.....".... rameterizations provide reasonable simulations of breaking
50'f- -CRISTA PrtIIIt 3 .. M5" 1. . 15 ... gravity waves [Liuet aI., 1999; Doyle etal., 2000], long-term
fine-scale simulations of wave breakdown beneath a critical
~40 level seem to require three-dimensional models [WilZtersand
D'Asaro, 1994; Dornbrack, 1998: Fritts and Werne, 2000].
~30
Additionally, the model here did not include mean flow evo
lilo
lution. which may be important in this problem. Thus, multi
day interactive runs using three-dimensional models may be
needed to describe these evolving mountain wave fields fully.
Acknowledgments. These simulations were made possible by
a grant of computing time on the Australian National University
Supercomputing Facility"s Fujitsu VPP300 vector supercomputer.
Figure 4. Black curve shows a vertical profile of temperalUre SDE acknowledges support for this research by the Office of Naval
perturbations at z = 845 km. 15 hours into Experiment C. Two Research and by NASA through the Atmospheric Chemistry Mod·
shaded solid curves reproduce the temperature perturbation pro eling and Analysis Program and the UARS Guest Investigator Pro
files acquired by CRISTA al locations 1 and 3 in Plate la (after gram. We thank D. Brouunan, A. DOmbrack. P. Preusse and two
Eckennann alld Preusse (\999]). reviewers for helpful comments on earlier drafts.
and PreU$se [19991. Amplitudes and vertical wavelengths REFERENCES
from CRISTA compare fairly well with model profiles. The
results showed that attenuated oscillations above 30 km were Bacmeisler, 1. T., Mountain-wave drag in the stratosphere and meso
sphere inferred from observed winds and a simple mountain-wave
the result of vertical wavelength reductions and intense wave
parameterization scheme.i. Armos. Sci.. 50• • 377-399.1993.
breaking, as conjectured by EckemlQlln and Preusse [19991.
Bacmeister, 1. T. . and M. R. Schoeberl. Breakdown of vertically
Recent analysis of satellite data by McLandress el al. [2000] propagating two-dimensional gravity waves forced by orography.
has shown that temperature fluctuations appear recurrently in i. Armos. Sci., 46. 2109-2134.1989.
the middle atmosphere over southern South America. Thus Boville, B. A. . Middleatmosphere version oftheCCM2 (MACCM2):
these breaking mountain waves may be relevant to the clima annual cycle and interannual variability, i. Geophys. Res .• 100.
tology of this region of the middle atmosphere [Garcia and 9017·9039,1995.
Boville, 1994]. Broad. A. S .. High resolution numerical-model integrations 10 vali·
date gravily-wave-drag parameterization schemes: a case study.
Presently we have a limited understanding of the ampli
Q. i. R. Meteorol. Soc .. 122. 1625-1653, 1996.
tudes and wavelengths of mountain waves radiated into the
Coy. L., and R. Swinbank. Characteristics of stratospheric winds
middle atmosphere by complex topography. Existing pa
and temperatures produced by data assimilation.i. Geophys. Res.
rameterizations make use of topographic elevation spectra, 102,25,763-25.781.1997.
focusing either on dominant peaks [e.g., Bacmeister, 1993] DOmbrack, A.. Thrbulent mixing by breaking gravity waves, i.
or their power-law shapes [e.g., Shutts, 1995] to specify ra· Fluid Mech .• 375. 113-141, 1998.
diated mountain wave fields. Our results, though limited to DOmbrack. A., M. Leutbecher, H. Volkert and M. Wirth. Mesoscale
forecasts of strntospheric mountain waves, Meterol. Appi., 5,
a specific two-dimensional section of the Andes, produced
117-126.1998.
stratospheric wave fluctuations with distinct vertical and hor DOmbrack, A., M. Leutbecher, R. Kivi and E. KYll), Mountain
izontal wavelengths. These horizontal wavelengths were wave-induced record low stratospheric temperatures above nonh
closely related to peaks in the power spectrum of the topo em Scandinavia. Tel/us. 51A. 951·963.1999.
graphic elevations h(.:c). lending some support to spectral Doyle. 1. D., et al., An intercomparison of model-predicted wave
parameterization methods. However, the various horizontal breaking for the 11 January 1972 Boulder windstorm. Mon. Wea.
Rev. • 128,901-914,2000.
wavelengths evolved differently with time in our model, due
Dumn. D. R. . Do breaking mountain waves decelerate the local
mostly to varying vertical group velocities. Wave fields were
mean flow?,i. Atmas. Sci. • 52. 4010-4032.1995.
further complicated at later times by breaking and turbulence. Dumn, D. R.. and J. B. Klemp, A compressible model for the
leading not only to increased damping of primary waves but simulation of moist mountain waves, Mon. Weo. Rev. . II J.
apparent generation of secondary waves. Even after 24 hours. 2341-2361.1983.
when simulations were terminated due to computational con Eckermann. S. D., and P. Preusse. Global measurements of strato
spheric mountain waves from space, Science, 286. 1534-1537,
straints, mountain waves in the middle atmosphere were s6ll
1999.
evolving. Fritts, D. c., and 1. A. Weme, Turbulence dynamics and mixing
Actual topography and flow fields here are intrinsically
due 10 gravity waves in the lower and middle atmosphere. this
three-dimensional [plate I b; Figure la; Seluchi et al. . 1998], volume.
which can influence mountain waves significantly [Shut/so Gal-Chen, T., and R. C. T. Sommerville. On the use of a coordinate
318 STRAT OSPHERlC MOUNTAIN WAVES OVER THE SOUTHERN ANDES
transfonnation for the solution of the Navier-Stokes equations.J. Minzner. R. A.. The 1976 standard atmosphere and its relationship
Compo Phys. . 17.209-228.1975. to earlier standards. Rev. Geophys. Space Phy:s .. 15, 255-264,
Garcia. R. R .. and B. A. Boville. "Downward control" of the mean 1977.
meridional circulation and temperature distribution of the polar SlItomura. T. • and K. Sato. Secondary generation of gravity waves
winter stratosphere. J. A/mos. Sci., 51.2238-2245, 1994. associated with the breaking of mountain waves. 1. Armos. Sci..
Grossmann. K. U .. Recent improvements in middle atmosphere 56. 3847-3858.1999.
remote sounding techniques: the CRISTA-SPAS experiment. this Schoeberl. M. R .. The penetration of mountain waves into the mid
volume. dle atmosphere,J. Amlo:s. Sci., 42. 2856-2864, 1985.
lkawa. M .. High-drag states and foehns of a two-layered stratified Seluchi. M., Y. V. Serafini and H. Le Treut, The impact of the
fluid past a two-dimensional obslacle. 1. Me/eorot. Soc. Japan., Andes on trnnsient atmospheric systems: a comparison between
68. 163-182,1990. observations and GeM results. Mall Wea. Rt!V., 126,895-912.
Jones, W. L .. Reflexion and stability of waves in stably stratified 1998.
fluids with shear flow: a numerical study. J. Fluid Mech .• 34, Shutts, G., Gravity-wave drag parameterization over complex ter
609-624. 1968. rain: the effect of critical level absorption in directional wind
Kim. y ..J .. and A. Arakawa. Improvement of orographic gravity shear. Q. J. R. Me/torol. Soc. . 121, 1005-1021,1995.
wave parameterization using a mesoscale gravity wave model. J, Shutts. G. 1. • Stationary gravity-wave structure in flows with di
Almos. Sci. . 52,1875-1902,1995. rectional wind shear. Q. 1. R. Me/eorof. Soc .. 124, 1421-1442,
Klemp. 1. B. . and R. B. Wilhelmson, The simulation of three 1998.
dimensional convective stonn dynwnics,J. Almos. Sci.,35, 1070- Tan. K. A .• and L. M. Leslie, Development of a non.hydrostatic
1096.1978. model for atmospheric modelling, in Computational Techniques
Laprise. 1. P. R. . An assessment of the WKBI approximation to mId Applications: CTAC97. edited by BJ. Noye. M.D. Teubner.
the vertical structure of linear mountain waves: implications for and A.W. Gill. pp. 679-686. World Scientific Press, Singapore.
gravity wave drag parameterization, J. Armos. Sci .. 50, 1469- 1998.
1487.1993. Volkert. H .• and O.lntes. Orographically forced stratospheric waves
Leutbecher. M., and H. Volkert. Stratospheric temperature anoma over nonhem Scandinavia. Geophys. Re:s. Lett., 19. 1205-1208.
lies and mounlain waves: A three-dimensional simulation using 1992.
a multi·scale weather prediction model. Geophys. Res. Lell. . 23, Wicker, L. 1 .. and W. C. Skamarock. A time-splitting scheme for the
3329-3332, 1996. elastic equations incorporating second-order Runge-KUlla time
Lilly, D. K. . On the numerical simulation of buoyant convection. differencing. Mon. Wta. Rev., 126. 1992-1999.1998.
Ttl/us. 14, 148-172. 1962. Winters. K.. B. . and E. A. 0' Asaro. Three-dimensional wave inSIa
Liu. H.-L .. P. B. Hays. and R. G. Roble. A numerical study of bility near a critical level. J. Fluid Mech .. 272. 255-284. 1994.
gravity wave breaking and impacts on turbulence and mean state,
J. Almos. Sci. . 56. 2152-2177.1999.
c.,
McLandress. M. 1. Alexander. and D. L. Wu. Microwave Limb
Sounder observations of gravity waves in the stratosphere: a
climatology and interpretation. J. Geophys. Res. • (in press). K. Tan. School of Mathematics. University of New Sooth Wales.
2000. Sydney. NSW 2052. Australia. (e-mail: [email protected])
Miller, M. J. and A. J. Thorpe. Radiation conditions for the lateral S. D. Eckennann. E. O. Hulburt Center for Space Research. Code
boundaries of limited-area numerical models, Q. J. R. Mtteorot. 7641.2. Naval Research Laboratory, Washington. DC 20375. (e
Soc .. 107. 615-628. 1981. mail: [email protected])