Decoherence on a two-dimensional quantum walk using four- and two-state particle

0.76 MB·English

by  C. M. Chandrashekar

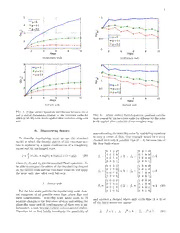
Decoherence in two-dimensional quantum walks using four- and two-state particles
C. M. Chandrashekar1,2,∗ and Th. Busch1,2,†
1Department of Physics, University College Cork, Cork, Republic of Ireland
2Quantum Systems Unit, Okinawa Institute of Science and Technology Graduate University, Okinawa, Japan
We study the decoherence effects originating from state flipping and depolarization for two-
dimensional discrete-time quantum walks using four-state and two-state particles. By quantifying
thequantumcorrelationsbetweentheparticleandpositiondegreeoffreedomandbetweenthetwo
spatial (x−y) degrees of freedom using measurement induced disturbance (MID), we show that
the two schemes using a two-state particle are more robust against decoherence than the Grover
walk, which uses a four-state particle. We also show that the symmetries which hold for two-state
quantum walks breakdown for the Grover walk, adding to the various other advantages of using
two-state particles over four-state particles.
3
1 I. INTRODUCTION and then following it by a conditional shift operation
0
2 Sˆ ≡(cid:88)[|0(cid:105)(cid:104)0|⊗|ψ (cid:105)(cid:104)ψ |+|1(cid:105)(cid:104)1|⊗|ψ (cid:105)(cid:104)ψ |].
x x−1 x x+1 x
Quantum walks are a close quantum analog of classi-
n x
a cal random walks, in which the evolution of a particle is (3)
J given by a series of superpositions in position space[1– The state after t steps of evolution is therefore given by

2 5]. Recently they have emerged as an efficient tool to
|Ψ (cid:105)=[Sˆ [Bˆ(θ)⊗1ˆ]]t|Ψ (cid:105). (4)
2 carry out quantum algorithms[6, 7] and have been sug- t x in
gested as an explanation for wavelike energy transfer All experimental implementations of quantum walks re-
]
h within photosynthetic systems[8, 9]. They have applica- ported by today have used effectively 1D dynamics. A
p tions in the coherent control of atoms and Bose-Einstein naturalextensionof1Dquantumwalkstohigherdimen-
- condensates in optical lattices[10, 11], the creation of sion is to enlarge the Hilbert space of the particle with
t
n topological phases[12], and the generation of entangle- one basis state for each possible direction of evolution at
a ment[13]. Quantum walks therefore have the potential the vertices. Therefore, the evolution has to be defined
u to serve as a framework to simulate, control and under- usinganenlargedcoinoperationfollowedbyanenlarged
q
stand the dynamics of a variety of physical and biologi- conditioned shift operation. For a two-dimensional (2D)
[
cal systems. Experimental implementations of quantum rectangular lattice the dimension of the Hilbert space of

3 walks in last few years have included NMR[14–16], cold the particle will be four and a four dimensional coin op-
v ions[17, 18], photons[19–24], and ultracold atoms[25], eration has to be used. Two examples of this are given
7
which has drawn further interest of the wider scientific by using either the degree four discrete Fourier opera-
8
2 community to their study. tor (DFO) [Fourier walk] or the Grover diffusion opera-
1 The two most commonly studied forms of quantum tor (GDO) [Grover walk] as coin operations[33–35]. An
4. walks are the continuous-time[26] and the discrete-time alternative extension to two and higher (d) dimensions
0 evolutions[5, 27–32]. In this work we will focus on the is to use d coupled qubits as internal states to evolve
2 discrete-timequantumwalkandjustcallitquantumwalk thewalk[36,37]. Boththesemethodsareexperimentally
1 for simplicity. If we consider a one-dimensional (1D) ex- demanding and beyond the capability of current exper-
v: ample of a two-state particle initially in the state imental set ups. Surprisingly however, two alternative
i schemes to implement quantum walks on a 2D lattice
X
were recently proposed which use only two-state parti-
r |Ψin(cid:105)=(cid:0)cos(δ/2)|0(cid:105)+eiηsin(δ/2)|1(cid:105)(cid:1)⊗|ψ0(cid:105), (1) cles. In one of these a single two-state particle is evolved
a
in one dimension followed by the evolution in other di-
mensionusingaHadamardcoinoperation[38,39]. Inthe
then the operators to implement the walk are defined
other,atwo-stateparticleisevolvedinonedimensionfol-
on the coin (particle) Hilbert space H and the position
c lowed by the evolution in the other using basis states of
Hilbert space H [H=H ⊗H ]. A full step is given by
p c p different Pauli operators as translational states[40, 41].
first using the the unitary quantum coin
Inthisworkweexpandtheunderstandingof2Dquan-
tum walks by studying the effects decoherence has on
(cid:20) (cid:21) the four-state Grover walk and the two two-state walks
cos(θ) sin(θ)
Bˆ(θ)≡ , (2) mentioned above. The environmental effects are mod-
sin(θ) −cos(θ)
eled using a state-flip and a depolarizing channel and we
quantifythequantumcorrelationsusingameasurebased
on the disturbance induced by local measurements [42].
∗Electronicaddress: [email protected] While in the absence of noise the probability distribu-
†Electronicaddress: [email protected] tions for all three schemes are identical, the quantum
2
correlations built up during the evolutions differ signifi- where |ψ (cid:105) = |ψ (cid:105)⊗|ψ (cid:105). It is well known that the
x,y x y
cantly. However, due to the difference in the size of the operation[Sˆ [Gˆ⊗1ˆ]]t resultsinmaximalspreadofthe
(x,y)
particles Hilbert space for the Grover walk and the two- probability distribution only for the very specific initial
statewalks,quantumcorrelationsgeneratedbetweenthe state
particleandthepositionspacecannotbecompared. The
1
quantumcorrelationsbetweenthetwospatialdimensions |Ψ4 (cid:105)= (|0(cid:105)−|1(cid:105)−|2(cid:105)+|3(cid:105))⊗|ψ (cid:105), (7)
in 2 0,0
(x−y), obtained after tracing out the particle state, on
the other hand, can be compared and we will show that whereas the walk is localized at the origin for any other
they are larger for the walks using the two-state parti- case[43, 44]. Choosing |Ψ4in(cid:105) and evolving it for t steps
cles. Whentakingtheenvironmentaleffectsintoaccount, one finds
we find that all three schemes lead to different proba- t t
(cid:88) (cid:88)
bility distribution and decoherence is strongest for the |Ψ4(t)(cid:105) = [A |0(cid:105)+B |1(cid:105)
(x,y),t (x,y),t
Grover walk, therefore making the two-state walks more x=−ty=−t
robust for maintaining quantum correlations. Interest- +C |2(cid:105)+D |3(cid:105)]⊗|ψ (cid:105) (8)
(x,y),t (x,y),t (x,y)
ingly, we also find that certain symmetries which hold
for the two-state quantum walk in the presence of noise where A(x,y),t, B(x,y),t, C(x,y),t and D(x,y),t are given by
do not hold for a Grover walk. Together with the spe- the iterative relations
cific initial state and the coin operation required for the 1
A = [−A +B
evolutionoftheGroverwalk, thisreducesthechancesto (x,y),t 2 (x+1,y+1),t−1 (x+1,y+1),t−1
identifyanequivalenceclassofoperationsonafour-state +C +D ] (9a)
(x+1,y+1),t−1 (x+1,y+1),t−1
particle to help experimentally implement the quantum
1
walk in any physical system that allows to manipulate B = [A −B
(x,y),t 2 (x+1,y−1),t−1 (x+1,y−1),t−1
the four internal states of the coin.
+C +D ] (9b)
This article is organized as follows : In SectionII we (x−1,y−1),t−1 (x+1,y−1),t−1
1
define the three schemes for the 2D quantum walk used
C = [A +B
tostudythedecoherenceandinSectionIIIwedefinethe (x,y),t 2 (x−1,y+1),t−1 (x−1,y+1),t−1
measure we use to quantify the quantum correlations. −C +D ] (9c)
(x−1,y+1),t−1 (x−1,y+1),t−1
In SectionIV, the effect of decoherence in the presence 1
D = [A +B
of a state-flip noise channel and a depolarizing channel (x,y),t 2 (x−1,y−1),t−1 (x−1,y−1),t−1
are presented and we compare the quantum correlations
+C −D ]. (9d)
(x−1,y−1),t−1 (x−1,y−1),t−1
betweenthexandydirectionsforthethreeschemes. We
finally show in Section V that the state-flip and phase- This results in the probability distribution
flip symmetries, which hold for the two-state quantum
t t
walk, breakdown for the four-state walk and conclude in P = (cid:88) (cid:88) (cid:104)|A |2+|B |2
4s (x,y),t (x,y),t
SectionVI.
x=−ty=−t
(cid:105)
+|C |2+|D |2 (10)
(x,y),t (x,y),t
II. TWO-DIMENSIONAL QUANTUM WALKS
which is shown in Fig.1 for t=25.
A. Grover walk
B. Alternate walk
For a Grover walk of degree four the coin operation is
given by[33, 34] Veryrecentlya2Dquantumwalkwassuggestedwhich
usedonlyatwo-stateparticlewhichwalksfirstonlyalong
−1 1 1 1 the x-axis followed by a step along the y-axis [38]. This
Gˆ = 1 1 −1 1 1, (5) walk can results in the same probability distribution as
2 1 1 −1 1 the Grover walk and its evolution is given by
1 1 1 −1
|Ψ (cid:105)=(Sˆ [Bˆ(θ)⊗1ˆ])(Sˆ [Bˆ(θ)⊗1ˆ])|Ψ (cid:105), (11)
1 (0,y) (x,0) in
and the shift operator is where
Sˆ ≡(cid:88)(cid:104)|0(cid:105)(cid:104)0|⊗|ψ (cid:105)(cid:104)ψ | Sˆ(x,0) ≡ (cid:88)(cid:2)|0(cid:105)(cid:104)0|⊗|ψx−1,y(cid:105)(cid:104)ψx,y|
(x,y) x−1,y−1 x,y
x,y
x,y
(cid:3)
+|1(cid:105)(cid:104)1|⊗|ψ (cid:105)(cid:104)ψ | (12a)
+|1(cid:105)(cid:104)1|⊗|ψ (cid:105)(cid:104)ψ | x+1,y x,y
x−1,y+1 x,y
+|2(cid:105)(cid:104)2|⊗|ψx+1,y−1(cid:105)(cid:104)ψx,y| Sˆ(0,y) ≡ (cid:88)(cid:2)|0(cid:105)(cid:104)0|⊗|ψx,y−1(cid:105)(cid:104)ψx,y|
(cid:105) x,y
+|3(cid:105)(cid:104)3|⊗|ψx+1,y+1(cid:105)(cid:104)ψx,y| , (6) +|1(cid:105)(cid:104)1|⊗|ψ (cid:105)(cid:104)ψ |(cid:3). (12b)
x,y+1 x,y
3
(cid:20) (cid:21)
0 1
states for x−axis and eigenstates of σˆ = , |+(cid:105) =
1 1 0
√1 (|0(cid:105) + |1(cid:105)) and |−(cid:105) = √1 (|0(cid:105) − |1(cid:105)) as basis states
2 2
for y−axis[40], which also implies that |0(cid:105) = √1 (|+(cid:105)+
2
|−(cid:105)) and |1(cid:105) = √1 (|+(cid:105) − |−(cid:105)). In this scheme a coin
2
operation is not necessary and each step of the walk can
be implemented by the operation
Sˆ ≡Sˆ (16)
σ3 (x,0)
followed by the operation
FIG.1: (Coloronline)ProbabilitydistributionfortheGrover Sˆ ≡(cid:88)(cid:104)|+(cid:105)(cid:104)+|⊗|ψ (cid:105)(cid:104)ψ |
after 25 steps. An identical distribution using the two-state σ1 x,y−1 x,y
particle with the |0(cid:105)√+i|1(cid:105) can be obtained using the alternate x,y
2 (cid:105)
walkwiththecoinoperationB(π/4)andthePauliwalkafter +|−(cid:105)(cid:104)−|⊗|ψ (cid:105)(cid:104)ψ | . (17)
x,y+1 x,y
25 steps.
The state after t steps of quantum walk is then given by
Using a coin operation with θ = π/4, the state of the |Ψ (cid:105) = [Sˆ Sˆ ]t|Ψ (cid:105)
walk after t steps can then be calculated as t σ1 σ3 in
t t
(cid:88) (cid:88) (cid:2) (cid:3)
|Ψ(t)(cid:105) = Wˆ(π/4)t|Ψ (cid:105) = A(x,y),t|0(cid:105)+B(x,y),t|1(cid:105) ⊗|ψx,y(cid:105),
in
x=−ty=−t
t t
(cid:88) (cid:88) (cid:2) (cid:3) (18)
= A |0(cid:105)+B |1(cid:105) ⊗|ψ (cid:105),
(x,y),t (x,y),t (x,y)
x=−ty=−t
where A and B are given by the coupled iter-
(x,y),t (x,y),t
(13)
ative relations
whereWˆ(π/4)=(Sˆ [Bˆ(π/4)⊗1ˆ])(Sˆ [Bˆ(π/4)⊗1ˆ]), 1(cid:104)
(0,y) (x,0) A = A +B
andA andB aregivenbythecouplediterative (x,y),t 2 (x+1,y+1),t−1 (x−1,y+1),t−1
(x,y),t (x,y),t
(cid:105)
relations
+A −B (19a)
(x+1,y−1),t−1 (x−1,y−1),t−1
1(cid:104)
1(cid:104)
A = A +A
(x,y),t 2 (x+1,y+1),t−1 (x−1,y+1),t−1 B(x,y),t = 2 B(x−1,y+1),t−1+A(x+1,y+1),t−1
(cid:105)
(cid:105)
+B −B (14a)
(x+1,y+1),t−1 (x−1,y+1),t−1 +B −A . (19b)
(x−1,y−1),t−1 (x+1,y−1),t−1
1(cid:104)
B = A −A
(x,y),t 2 (x+1,y−1),t−1 (x−1,y−1),t−1 The probability distribution
(cid:105)
+B +B . (14b) t t
(x+1,y−1),t−1 (x−1,y−1),t−1 P = (cid:88) (cid:88) (cid:2)|A |2+|B |2(cid:3) (20)
2sσ (x,y),t (x,y),t
The resulting probability distribution is then x=−ty=−t
t t isagainequivalenttothedistributionobtainedusingthe
P = (cid:88) (cid:88) (cid:2)|A |2+|B |2(cid:3), (15) Grover walk and therefore also to the alternative walk
2s (x,y),t (x,y),t
x=−ty=−t for the initial state |Ψin(cid:105) = √1 (|0(cid:105)+i|1(cid:105))⊗|ψ0,0(cid:105) (see
2
Fig.1).
which for the initial state |Ψin(cid:105)= √1 (|0(cid:105)+i|1(cid:105))⊗|ψ0,0(cid:105) WhiletheshiftoperatorfortheGroverwalkisdefined
2
gives the same probability distribution as the four-state by a single operation, experimentally it has to be imple-
Grover walk (see Fig.1). mented as a two shift operations. For example, to shift
thestate|0(cid:105)from(x,y)to(x−1,y−1),ithasfirsttobe
shifted along one axis followed by the other, very simi-
C. Pauli walk larlytothewayitisdoneinthetwo-statequantumwalk
schemes. Therefore,atwo-statequantumwalkin2Dhas
A further scheme to implement a 2D quantum walk many advantages over a four-state quantum walk. The
using only a two-state particle can be constructed using two-state walk using different Pauli basis states for the
different Pauli basis states as translational states for the different axes has the further advantage of not requir-
two axis. For convenience we can choose the eigenstates ingacoinoperationatall,makingtheexperimentaltask
(cid:20) (cid:21)
1 0 even simpler in physical systems where access to differ-
of the Pauli operator σˆ = , |0(cid:105) and |1(cid:105) as basis
3 0 −1 ent Pauli basis states as translational states is available.
4
One can, of course, also consider including a coin opera-
tion in the Pauli walk, which would result in a different
probability distributions [41].
For general initial states, quantum walks in 2D with a
coinoperation∈U(2)canresultinamanynon-localized
probability distribution in position space. This is a fur-
ther difference to the Grover walk which is very specific
with respect to the initial state of the four-state particle
and the coin operation.
III. MEASUREMENT INDUCED
DISTURBANCE
Quantifyingnon-classicalcorrelationsinherentinacer-
tain state is currently one of the most actively studied
topics in physics (see for example [45]). While many
of the suggested methods involve optimization, making
themcomputationallyhard,Luo[42]recentlyproposeda
computablemeasurethatavoidsthiscomplication: ifone
considers a bipartite state ρ living in the Hilbert space
H ⊗H ,onecandefineareasonablemeasureoftheto-
A B
tal correlations between the systems A and B using the
mutual information
I(ρ)=S(ρ )+S(ρ )−S(ρ), (21)
A B
where S(·) denotes von Neumann entropy and ρ and
A
ρ are the respective reduced density matrices. If ρ =
(cid:80)B pj Πj and ρ = (cid:80) pj Πj , then the measuremAent FIG. 2: (Color online) Quantum correlations Q(ρpp) and
j A A B j B B Q(ρ ) for the different schemes in the absence of noise.
inducedbythespectralcomponentsofthereducedstates xy
is
(cid:88) sizeoftheparticlesdegreeoffreedomfortheGroverand
Π(ρ)≡ Πj ⊗ΠkρΠj ⊗Πk. (22)
A B A B the two-state walks, a direct comparison of the quantum
j,k correlationsQ(ρ )doesnotmakesense. Amongthetwo-
pp
state schemes on the other hand, we see that the Pauli
GiventhatI[Π(ρ)]isagoodmeasureofclassicalcorrela-
walk has a larger Q(ρ ) in comparison to the alternate
tions in ρ, one may consider a measure for quantum cor- pp
walk.
relations defined by the so-called Measurement Induced
A fair comparison between all systems can be made
Disturbance (MID) [42]
by looking at the quantum correlations generated be-
tween the two spatial dimensions x and y, Q(ρ ) (see
Q(ρ)=I(ρ)−I[Π(ρ)]. (23) xy
Fig.2(b)). ρ is obtained by tracing out the particle
xy
MID does not involve any optimization over local mea- degree of freedom from from complete density matrix
surements and can be seen as a loose upper bound on [ρ˜4s(t), ρ˜2s(t)andρ˜2sσ(t)]comprisingoftheparticleand
quantum discord [46]. At the same time it is known to the position space. We find that Q(ρxy) is identical for
capture most of the detailed trends in the behaviour of both two-state schemes and exceeding the Grover walk
quantumcorrelationsduringquantumwalks[47]. There- result. This behaviour is similar to the one described in
fore, we will use MID (Q(ρ)) in the following to quantify Refs. [38, 39], where the entanglement created during
quantum correlations for the different 2D quantum walk the Grover walk was compared with the alternate walk
evolutions. using the negativity of the partial transpose, in its gen-
Despite having the same probability distributions in eralization for higher-dimensional systems [48, 49].
the absence of noise, the MIDs for the four-state walk
and the two-state walks differ. In Fig.2(a) we show the
MIDbetweentheparticleandthepositiondegreeoffree- IV. DECOHERENCE
dom, Q(ρ ) for all three walks and find that it is signif-
pp
icantly higher for the Grover walk. Where ρ is ρ˜ (t) The effects of noise on 1D quantum walks has been
pp 4s
for Grover walk, ρ˜ (t) for alternate walk and ρ˜ (t) for widely studied [47, 50–53] but the implications in 2D
2s 2sσ
the Pauli walk. However, due to the difference in the settings are less well known [37, 54, 55]. In particular no
5
(a) (b)
FIG. 3: (Color online) Probability distribution of the Grover
walk when subjected to a different state-flip noise level with
k=23after15steps. (a)and(b)arefornoiselevels,p=0.1
and p=0.9, respectively.
study has been done on either of the two-state schemes
presented in the previous section and we therefore now
comparetheirdecoherencepropertiestotheGroverwalk,
using a state-flip and a depolarizing channel as noise
models. We show that this leads to differing probability
distributions and has an effect on the amounts of quan-
tum correlations as well.
A. State flip noise
1. Grover walk FIG. 4: (Color online) Quantum correlations created by the
Grover walk in the presence of a noise channel including all
possible state flips (k=23).
Foratwo-stateparticle,state-flipnoisesimplyinduces
(cid:20) (cid:21)
0 1
abitflip[σ = ]butfortheGroverwalk,thestate-
1 1 0
2. Two-state walks
flipnoiseonthefourbasisstatescanchangeonestateto
23 other possible permutations. Therefore, the density
matrix after t steps in the presence of a state-flip noise The evolution of each step of the two-state quantum
channel can be written as walkcomprisesofamovealongoneaxisfollowedamove
along the other. Therefore, the walk can be subjected to
(cid:34) k (cid:35) a noise channel after evolution along each axis or after
ρˆ (t) = p (cid:88)fˆSˆ ρˆ (t−1)Sˆ †fˆ† eachfullstepofthewalk. Inthefirstcase,thenoiselevel
4s k i 4 4s 4 i p(cid:48) = p isappliedtwotimesduringeachstepinodertobe
i=1 2
+(1−p)[Sˆ ρˆ (t−1)Sˆ †], (24) equivalent to the application of a noise of strength p in
4 4s 4
the second case. For the alternate walk the evolution of
the density matrix with a bit-flip noise channel applied
where p is the noise level, S =Sˆ [Gˆ⊗1ˆ], and the fˆ
4 (x,y) i after evolution along each axis is then given by
arethestate-flipoperations. Foranoisychannelwithall
the 23 possible flips one has k =23 and in Figs.3(a) and p(cid:104) (cid:105)
ρˆ(cid:48) (t)= σˆ Sˆ ρˆ (t−1)Sˆ†σˆ†
3(b) we show the probability distribution of the Grover 2s 2 1 x 2s x 1
for weak (p=0.1) and strong (p=0.9) noise levels after (cid:16) p(cid:17)(cid:104) (cid:105)
+ 1− Sˆ ρˆ (t−1)Sˆ† (25a)
15 step. Compared to the distribution in the absence of 2 x 2s x
noise(seeFig.1)aprogressivereductioninthequantum p(cid:104) (cid:105)
ρˆ (t)= σˆ Sˆ ρˆ(cid:48) (t)Sˆ†σˆ†
spread is clearly visible. Note that for p = 1 the walk 2s 2 1 y 2s y 1
corresponds to a fully classical evolution. +(cid:16)1− p(cid:17)(cid:104)Sˆ ρˆ(cid:48) (t)Sˆ†(cid:105), (25b)
InFig.4(a)weshowthequantumcorrelationsbetween 2 y 2s y
the particle state with the position space, Q(ρ ), as a
pp (cid:20) (cid:21)
0 1
functionofnumberofstepst. Withincreasingnoiselevel, where σˆ = ⊗1ˆ, Sˆ = Sˆ [Bˆ(θ)⊗1ˆ], and Sˆ =
1 1 0 y (0,y) x
adecreaseinQ(ρ )isseen,whereasforthequantumcor-
pp
relationsbetweenthexandyspatialdimensions,Q(ρ ), Sˆ [Bˆ(θ)⊗1ˆ].
xy (x,0)
the same amount of noise mainly leads to a decrease in Similarly, the density matrix with a bit-flip noise ap-
the positive slope (see Fig.4(b)). plied after the evolution along each axis for the Pauli
6
(a)Alternatewalk (b)Alternatewalk
(a)Alternatewalk
(c)Pauliwalk (d)Pauliwalk
FIG. 5: (Color online) Probability distributions of the two-
state walk with the bit-flip noise applied after evolution in
each direction. The strength of the noise is p/2=0.05 in (a)
and (c) and p/2=0.45 in (c) and (d) and the evolution was
carried out for 25 step each time.
walk is given by
p(cid:104) (cid:105)
ρˆ(cid:48) (t)= σˆ Sˆ ρˆ (t−1)Sˆ† σˆ† (b)PauliWalk
2sσ 2 1 σ3 2sσ σ3 1
(cid:16) p(cid:17)(cid:104) (cid:105)
+ 1− 2 Sˆσ3ρˆ2sσ(t−1)Sˆσ†3 (26a) FIG.6: (Coloronline)Particle-positionquantumcorrelations
createdbythetwo-statewalksfordifferentbit-flipnoiselevels
p(cid:104) (cid:105)
ρˆ (t)= σˆ Sˆ ρˆ(cid:48) (t)Sˆ† σˆ† applied after evolution along each axis.
2sσ 2 1 σ1 2sσ σ1 1
(cid:16) p(cid:17)(cid:104) (cid:105)
+ 1− Sˆ ρˆ(cid:48) (t)Sˆ† . (26b)
2 σ1 2sσ σ1
The density matrix for the second case, that is, with
a noisy channel applied only once after one full step of
In Figs.5(a) and 5(b) the probability distributions for
walk evolution, for both two-state walks is given by
the alternate walk after 25 steps of noisy evolution with
p = 0.1 and p = 0.9 are shown and Figs.5(c) and 5(d) (cid:104) (cid:105)
ρˆ (t)=p σˆ Qˆ(t−1)σˆ† +(1−p)Qˆ(t−1) (27a)
show the same for the Pauli walk. It can be seen that 2s 1 1
thebit-flipnoisechannelactssymmetricallyonbothaxes ρˆ (t)=p(cid:104)σˆ Qˆ (t−1)σˆ†(cid:105)+(1−p)Qˆ (t−1) (27b)
for the alternate walk, but asymmetrically on the Pauli 2sσ 1 σ 1 σ
walk. Thisisduetothefactthatthebit-flipnoiseapplied
where
along the axis in which the σ Pauli basis is used leaves
1
the state unchanged. A completely classical evolution is
Qˆ(t−1)=Sˆ Sˆ ρˆ (t−1)Sˆ†Sˆ† (28a)
recovered for p = 1 (p(cid:48) = 0.5) and an evolution with y x 2s x y
p=2 is equivalent to one with p=0. Qˆ (t−1)=Sˆ Sˆ ρˆ (t−1)Sˆ† Sˆ† . (28b)
σ σ1 σ3 2sσ σ3 σ1
Evolving the density matrix and calculating the MID
for a noiseless evolution (p=0), one can see from Fig. 6 Inthiscasemaximumdecoherenceandacompletelyclas-
that the initial difference in Q(ρ ) between the Pauli sical evolution is obtained for p = 0.5 and the evolution
pp
walk and the alternate walk decreases during the evolu- with p = 1 is equivalent to the one with p = 0. The ob-
tion and eventually both values settle around 1.5. For a tained probability distributions are almost identical for
noisy evolution, however, the initial difference in Q(ρ ) bothwalksanddifferonlyslightlyfromtheonesobtained
pp
does not decrease over time and we find a higher value for the alternate walk with noise applied after evolution
forthePauliwalkcomparedtothealternatewalk. Simi- along each axis (see Fig.5(a) and 5(b)). The correlation
larly,carefulexaminationofFig.7showsthattheQ(ρ ) functionsQ(ρ )andQ(ρ )behaveverysimilarforboth
xy pp xy
forthealternatewalkandthePauliwalkareidenticalin walks (see Figs. 8 and 9) and we can conclude that the
the absence of noise, but differ for noisy evolution, with presence of bit-flip noise on both two-state walks when
thealternatewalkbeingaffectedstrongerthanthePauli applied after a full step leads to equally strong decoher-
walk. ence.
7
(a)Alternatewalk (a)Alternatewalk
(b)Pauliwalk (b)Pauliwalk
FIG. 7: (Color online) Quantum correlations between the x
and y spatial dimensions created by the two-state walks for FIG. 8: (Color online) Particle-position quantum correla-
differentbit-flipnoiselevelsappliedafterevolutionalongeach tionscreatedbythetwo-statewalksfordifferentbit-flipnoise
axis levels applied after evolution of one complete step.
B. Depolarizing channel
approximatingthestateflipnoisebyrestrictingourselves
to only a subset of flips. One example would be a noisy
To describe depolarizing noise we use the standard
channel with only 6 possible flips (k =6) between two of
model in which the density matrix of our two-state sys-
the four basis states
tem is replaced by a linear combination of a completely
mixed and an unchanged state,
0 1 0 0 0 0 1 0
p 1 0 0 0 0 1 0 0
ρˆ= 3(σˆ1ρˆσˆ1+σˆ2ρˆσˆ2+σˆ3ρˆσˆ3)+(1−p)ρˆ, (29) fˆ1 =0 0 1 0⊗1ˆ ; fˆ2 =1 0 0 0⊗1ˆ
0 0 0 1 0 0 0 1
whereσˆ ,σˆ andσˆ arethestandardPaulioperators. To
1 2 3
beabletocomparetheeffectsofthedepolarizingchannel 0 0 0 1 1 0 0 0
ontheGroverwalkandthetwo-statewalkswewillapply fˆ =0 1 0 0⊗1ˆ ; fˆ =0 0 1 0⊗1ˆ
the noise only once after each full step. 3 0 0 1 0 4 0 1 0 0
1 0 0 0 0 0 0 1
1 0 0 0 1 0 0 0
1. Grover walk 0 0 0 1 0 1 0 0
fˆ = ⊗1ˆ ; fˆ = ⊗1ˆ (30)
5 0 0 1 0 6 0 0 0 1
Forthefour-stateparticlethedepolarizingnoisechan- 0 1 0 0 0 0 1 0
nel comprises of all possible state flips, phase flips and
their combinations. State-flip noise alone leads to 23
and another a channel where only cyclic flips (k = 3) of
possible changes in the four-state system and adding the
all the basis states can appear
phase-flip noise and all combinations of these two is un-
fortunately a task beyond current computational ability.
Therefore let us first briefly investigate the possibility of fˆ =fˆ⊗1ˆ ; fˆ =fˆ2⊗1ˆ ; fˆ =fˆ3⊗1ˆ (31)
1 2 3
8
(a)Alternatewalk
FIG. 10: (Color online) Quantum correlations between the x
andyspatialdimensionsfortheGroverwalkinthepresenceof
astate-flipnoisechannelwithp=0.1. Thenoiseismodelled
asstate-flipsincludingallpossibleflips(k=23),flipsbetween
only two of the basis states (k=6) and cyclic flips of all the
four basis state (k=3)
(b)Pauliwalk
(a) (b)
FIG. 9: (Color online) Quantum correlations between the
FIG. 11: (Color online) Probability distribution of (a) the
x and y spatial dimensions created by the two-state walks
Grover walk and (b) the two-state walks when subjected to
fordifferentbit-flipnoiselevelsappliedafterevolutionofone
a depolarizing channel. For the Grover walk the channel is
complete step.
given by Eq. (33) and for all walks the noise level is p=0.1.
The distribution is shown after 15 steps of evolution.
0 1 0 0
0 0 1 0 1 0 0 0 
with fˆ=  . The probability distributions for
01 00 00 10 where rˆ=00 ω0 ω02 00  with ω =e2π4i.
thesetwoapproximationsarevisuallyverysimilartothe 0 0 0 ω3
situation where all possible state-flips are taken into ac- Boththeseapproximationsforstate-flipandphase-flip
count (k = 23) and in Fig. 10 we compare the results noise will makes the complex depolarization noise man-
obtained for the the x−y spatial quantum correlations ageable for numerically treatment. The density matrix
for a noise level of p=0.1. of the Grover walk can then be written as
One can see that the spatial quantum correlations are (cid:34) 3 (cid:35)
affected stronger by the k = 3 than by the full k = 23 ρˆ (t) = p (cid:88)fˆSˆ ρˆ (t−1)Sˆ †fˆ†
flip noise. This implies that the two- and three state 4s 15 i 4 4s 4 i
i=1
flips included in k = 23 acts as reversals of cyclic flips,  
3
tfohrertehbeyderecdreuacsiengoftthheeeqffueacnttuomf ncooirsree.latSioinncaerethfeuntcrteinodns- + 1p5(cid:88)rˆjSˆ4ρˆ4s(t−1)Sˆ4†rˆj†
j=1
ally similar for k = 3,6 and 23, we will use the model
 
with k = 3 cyclic flips as the state-flip noise channel 3 3
for the Grover walk in this section. Similarly, taking + 1p5(cid:88)(cid:88)rˆjfˆiSˆ4ρˆ4s(t−1)Sˆ4†fˆi†rˆj†
intoaccountthecomputationallimitationsandfollowing i=1j=1
the model adopted for the state-flip, we will use a cyclic +(1−p)[Sˆ ρˆ (t−1)Sˆ †] (33)
phase-flips to model the phase-flip noise, 4 4s 4
andtheprobabilitydistributionforthiswalkisshownin
rˆ =rˆ⊗1ˆ ; rˆ =rˆ2⊗1ˆ ; rˆ =rˆ3⊗1ˆ, (32) Fig.11(a) for p=0.1. The quantum correlations Q(ρ )
1 2 3 pp
9
(a)Groverwalk (a)Alternatewalk
(b)Groverwalk (b)Pauliwalk
FIG.12: (Coloronline)Quantumcorrelationscreatedbythe FIG. 13: (Color online) Particle-position quantum correla-
Grover walk for different depolarizing noise levels. tionscreatedbythetwo-statewalksfordifferentdepolarizing
noise levels.
(cid:20) (cid:21) (cid:20) (cid:21) (cid:20) (cid:21)
and Q(ρ ) are shown in Fig.12. With increasing noise 0 1 0 −i 1 0
xy whereσˆ = ⊗1ˆ,σˆ = ⊗1ˆ,σˆ = ⊗1ˆ
level, a decrease in Q(ρ ) is seen, whereas for the quan- 1 1 0 2 i 0 3 0 −1
pp
tumcorrelationsbetweenthexandy spatialdimensions, and Qˆ(t−1) and Qˆ (t−1) are given by Eqs.(28a) and
σ
Q(ρ ), the same amount of noise mainly leads to a de-
xy (28b).
crease in the positive slope (see Fig.12). From this we
Similarly to the situation where we considered only
can conclude that the general trend in the quantum cor-
state-flip noise after one complete step (see Figs.8 and
relaltion due to state-flip noise (Fig.4) and depolarizing
9) we find again that the quantum correlations for both
noise is the same but the effect is slightly stronger when
walks behave nearly identical and only differ slightly in
including the depolarizing channel.
strength compared to the case of state-flip noise alone
(see Figs.13 and 14).
2. Two-state walks
C. Robustness of two-state walk
The depolarizing channels for the alternate walk and From the preceding sections we note that the x − y
Pauli walk can be written as spatial correlations, Q(ρ ), have a larger absolute value
xy
forthetwo-statewalkscomparedtotheGroverwalkand
ρˆ (t)= p(cid:34)(cid:88)3 σˆ Qˆ(t−1)σˆ†(cid:35)+(1−p)Qˆ(t−1) that the presence of noise affects all schemes in a similar
2s 3 i i manner. To quantify and better illustrate the effect the
i=1 noise has we therefore calculate
(34a)
Q(ρ ) for noisy walk
(cid:34) 3 (cid:35) R(ρ )= xy , (35)
ρˆ (t)= p (cid:88)σˆ Qˆ (t−1)σˆ† +(1−p)Qˆ (t−1), xy Q(ρxy) for noiseless walk
2sσ 3 i σ i σ
i=1 as a function of number of steps, which gives the rate
(34b)
of decrease in the quantum correlations. In Figs.15 and
10
(a)Alternatewalk
FIG.16: (Coloronline)Relativedecayofthequantumcorre-
lationsQ(ρ )inthepresenceofadepolarizingnoisechannel
xy
with p=0.2.
V. BREAKDOWN OF STATE-FLIP AND
PHASE-FLIP SYMMETRIES FOR FOUR-STATE
WALKS
The quantum walk of a two-state particle in 1D is
(b)Pauliwalk known to remain unaltered in the presence of unitary
operations which equally effect each step of the evolu-
tion. This is due to the existence of symmetries[52, 53],
FIG. 14: (Color online) Quantum correlations between the x which can help to identify different variants of the same
and y spatial dimensions created by the two-state walks for quantum walk protocol and which can be useful in de-
different depolarizing noise levels. signing experimental implementation. For example, in
a recent scheme used to implement a one-dimensional
quantum walk using atoms in an optical lattice[56], the
16 we show this quantity in the presence of state-flip conditional shift operator also flipped the state of the
or depolarizing noise, respectively, for a noise level of atom with every shift in position space. However, the
p=0.2. One can clearly see that in both cases the two- existence of a bit-flip symmetry in the system allowed to
statewalksaremorerobustagainstthenoiseatanypoint implement the walk without the need for compensation
during the evolution. Note that the Grover walk only ofthesebit-flips. Inthissectionwelookatpossiblesym-
producescorrelationsfromstep2on,whichisthereason metries in the walks discussed above and show that the
for its graph starting later. bit-flip and phase-flip symmetries, which are present in
the evolution of the two-state particle are absent in the
evolution of the four-state particle.
The density matrix for a two-state quantum walk in
the presence of a noisy channel will evolve through a
linear combination of noisy operations on the state and
the unaffected state itself. As an example we illustrate
the symmetry due to bit-flip operations in the alternate
walk with bit-flip noise after evolution of one complete
step. The density matrix in this case is given by
(cid:104) (cid:105)
ρˆ (t) = p σˆ Sˆ Sˆ ρˆ (t−1)Sˆ†Sˆ†σˆ†
2s 1 y x 2s x y 1
(cid:104) (cid:105)
+(1−p) Sˆ Sˆ ρˆ (t−1)Sˆ†Sˆ† , (36)
y x 2s x y
FIG. 15: (Color online) Relative decay of the quantum cor-
rweiltahtipon=s Q0.(2ρ.xy) in the presence of a state-flip noise channel whereσˆ1 =(cid:20)01 10(cid:21)⊗1ˆ. Whenthenoiselevelisp=1this