Coupled $S=1/2$ Heisenberg antiferromagnetic chains in an effective staggered field

0.32 MB·English

by  Masahiro Sato

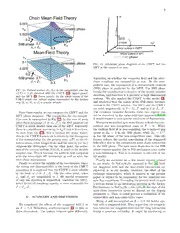
1
Coupled S = Heisenberg antiferromagnetic chains in an effective staggered field
2
Masahiro Sato and Masaki Oshikawa
Department of Physics, Tokyo Institute of Technology,
Oh-okayama, Meguro-ku, Tokyo 152-8550, Japan
We present a systematic study of coupled S = 1/2 Heisenberg antiferromagnetic chains in an
effective staggered field. We investigate several effects of the staggered field in the higher (two or
4 three) dimensional spin system analytically. In particular, in the case where the staggered field
0
and the inter-chain interaction compete with each other, we predict, using mean-field theory, a
0
characteristicphasetransition. Thespin-wavetheorypredictsthatthebehaviorofthegapsinduced
2
bythestaggeredfieldisdifferentbetweenthecompetitivecaseandthenon-competitivecase. When

n the inter-chain interactions are sufficiently weak, we can improve the mean-field phase diagram by
a using chain mean-field theory and theanalytical results of field theories. The ordered phase region
J predictedbythechainmean-fieldtheoryissubstantiallysmallerthanthatbythemean-fieldtheory.

0
3 PACSnumbers: 75.10.Jm

]
l I. INTRODUCTION known examples are Cu-benzoate,6,7,8 [PM Cu(NO )
-e (H2O)2]n (PM=pyrimidine),9 and Yb4As3.1·0,11,12 A3ll2of·
r
t Theeffectsinducedbymagneticfieldsinmagnetshave these have low-symmetry crystal structures which allow
.s been a subject of theoretical research interest for a long a staggered g tensor and a DM interaction along the
at time. Inparticular,recentlythe magnetizationprocesses chain.13 It is expected in Refs. 1,14 and 5 that the stag-
m ofvariousspinchainsandladdershavebeeninvestigated gered field induces an excitation gap in the S = 1/2
intensively. Owing to the progress of the various experi- Heisenbergantiferromagnetic(HAF)chain,whichshould
-
d mentalmethods,therehasbeenanincreasingconnection be otherwise gapless. The excitation gap caused by the
n betweenthetheoriesandtheexperiments. Insuchacon- staggered field is indeed found in these materials.6,9,12
o text, one of the new attractive subjects in magnetism is Moreover, low-temperature anomalies in physical quan-
c
[ the effects of a staggered magnetic field, namely, a mag- tities, such as the susceptibility and the electron spin
netic field which changes direction alternatingly. While resonance line-width,15,16 are also successfully explained

1 it may soundunrealistic, there exist atleastthree mech- as effects of the staggered field5. Thus it is confirmed
v anisms generating the staggered fields in real magnets, that they are described by an S =1/2 HAF model with
7
as discussed in Refs. 1 and 2. an effective staggeredfield.
2
6 The first mechanism is due to the staggeredgyromag- Thereisanother,ratherdifferent,mechanismtogener-
1 netic(g)tensor,whichcanbepresentifthecrystalstruc- ateastaggeredfield. Letussupposethatthesystemcon-
0 tureisnottranslationallyinvariant. Thestaggeredgten- sistsoftwosublattices,withaweakinter-latticecoupling
4 sor gst is defined in the coupling between the spin and and strong intra-lattice one. If one of the sublattices is
0 the eαxβternal magnetic field (Zeeman term) as N´eel ordered, the inter-lattice coupling, as a mean field,
/
t could give an effective staggered field on the other sub-
a
m HˆZeeman =−µB Hα[gαuβ +(−1)jgαstβ]Sjβ, (1) lwahtteircee.RTihsearmeaalgiznaettiiocnroafretheiasrtshce,naanrdiotihseinR-Rio2nBalaNttiOice3
j
- X provides a staggered field for Ni chains (S =1).17,18
d
n where H~ =(Hx,Hy,Hz) is an applied uniform magnetic Actually all the materials discussed above are highly
o fieldandSβ isthespinoperatorofthelocalmagneticmo- one-dimensional (1D). However, at lower temperature
c ment. Herje H gst is nothing but an effective staggered andlowerenergy,the inter-chaininteractionwill eventu-
v: field. Inadditiαonα,βthestaggeredfieldmayalsoarisefrom allybedominant. Inaddition,therearereportsonafew
Xi the staggeredDzyaloshinskii-Moriya(DM) interaction3,4 materials[CuCl2·2DMSO(DMSO=dimethylsulphoxide)
(Refs. 19,20,21) and BaCu (Si Ge ) O (Refs. 22)]
2 1−x x 2 7
r
which seem to have an effective staggered field and also
a
Hˆ = ( 1)jD~ S~ S~ , (2) a relatively large inter-chain interaction. Therefore the
DM j j+1
− · × work including the inter-chain interaction could be rele-
Xj (cid:16) (cid:17) vant for experiments.
which can be present if the crystal symmetry is suffi- Given these backgrounds, in the present paper, we
ciently low. It is shown in Refs. 1and 5 that in the pres- would like to clarify the characteristic roles of staggered
enceofthestaggeredDMinteractionalongthe chain,an fields in higher dimensional spin systems. In this pa-
applied uniform field H~ also generates an effective stag- per,we areconcernedwith dimensionshigher than 1 but
gered field ~h D~ H~. Several quasi-one-dimensional stillrealisticincondensedmatterphysics,namely,twoor
∝ ×
Heisenberg antiferromagnets are now known to have the three dimensions. However, most of the analyses in this
staggered field due to the above mechanisms. The well paperapplystraightforwardlyeventofourdimensionsor
2
higher. H
weakly coupled direction
Varieties of spin models with effective staggered fields
are conceivable. As a simplest model including both the h
staggered field and the inter-chain coupling, in this pa-
per, we concentrate on the following S = 1/2 spatially J
⊥
anisotropic Heisenberg Hamiltonian
Hˆ = JS~ S~ +J S~ S~ (3) J
i,j,k i+1,j,k ⊥ i,j,k i,j+1,k
· ·
X~r (cid:16)
+J′ S~ S~
⊥ i,j,k· i,j,k+1
(cid:17) z
H Sz h ( 1)iSx , S
− i,j,k− − i,j,k
X~r X~r y
S
x
where S~i,j,k is the spin 1/2 operator on ~r =(i,j,k) site. strongly coupled direction S
ThecouplingconstantsarerestrictedtoJ > J J′ ,
| ⊥|≥| ⊥|
andthustheidirectionisthestronglyantiferromagnetic
FIG. 1: Directions of the magnetic fields and the spin mo-
(AF) coupled one. The system with J⊥′ = 0 is 2D, in mentsinthe2Dcompetitivecase. Theshortblackarrowsare
whichtheindexkvanishes. Thelasttwotermsrepresent thespinmomentsprojectedontospinxyplaneintheordered
the uniform and staggered Zeeman terms respectively. phase (spontaneous symmetry breaking phase, see text) ex-
pected by the MFT. The gray arrows indicate the direction
In our model (3), one can immediately find that when
of the staggered field h. The uniform field H is applied per-
the inter-chain interactions are AF, they compete with
pendicular tothis paper.
the staggeredZeemanenergy,while in the ferromagnetic
(FM) case, both the interactions and the staggered field
h jointly make a N´eel state stable. Let us refer the AF
case as the competitive case, and the FM case as the II. MEAN-FIELD THEORY APPROACH
non-competitive one. As will be explained later on, we
predictthatthecompetitionbringsasecond-orderphase
In this section, we treat the model (3) within mean-
transition in the competitive case. Its emergence is one
fieldtheory(MFT)framework. Wefirstdiscussthecom-
of the mostcharacteristiceffects ofthe staggeredfield in
petitive case, and then touch the non-competitive case
our higher dimensional spin model.
briefly.
Therestofthispaperisorganizedasfollows. InSec.II,
In the competitive case, considering the advantage of
weapplymean-fieldtheorytothemodel(3). Inthecom-
both the inter-chain energy and the staggered Zeeman
petitive case a phase transition is predicted. Since we
energy as well as the intra-chain coupling J, we can ex-
are primarily interested in the transition, which is char-
pect that the spin moment turns as Fig. 1 at sufficiently
acteristic for the higher dimensional system, in the later
lowtemperatureandsmallfieldscomparabletotheinter-
sectionswewillmainlydiscussthecompetitivecase. The
chain couplings. The assumed spin moment is
non-competitive case is touched as a comparison to the
competitivecase. Besidesthephasediagrams,themean-
field magnetizationcurves and critical exponents are de- S~i,j,k MFT = ( 1)imx, ( 1)i+j+kmy, mz . (4)
h i − −
rivedfromtheself-consistentequations. InSec.III,using
(cid:0) (cid:1)
linear spin-wave approximation,we derive the spin-wave The choice of the mean field (4) is presumably valid as
dispersions in the the competitive case and in the non- long as J is sufficiently larger than J and J′ . On the
⊥ ⊥
competitivecase. Asaresult,wefindthattheexcitation other hand, for instance, in the limiting case: J 0,
→
gapinducedbythestaggeredfieldbehavesdifferentlybe- where the model is reduced to a 2D or 1D AF one with
tweenthecompetitivecaseandthenon-competitivecase. a uniform field, there are possibilities that Sx,z are in-
h j,ki
In Sec. IV, we improve the mean-field phase diagrams homogeneous along the j or k directions, and thus Eq.
by using chain mean-field theory.23,24 The latter is ex- (4)is invalid. In this paper, the MFT in the competitive
pected to be superior, when the inter-chain interactions case is performed only within the mean field (4).
are weak and the effective 1D model can be solved ex- The minimal condition for the mean-field free energy
actly. The improved diagram shows that in the weakly gives the following self-consistent equations:
couplingregionofthecompetitivecase,theorderedphase
becomes much narrower than the mean-field prediction. ǫ
α
m = tanh(βǫ), (5a)
In the last section, we summarize those results and dis- α 2ǫ
cuss future problems. In Appendix, the details of the 1
spin-wave results are given. m2 = tanh2(βǫ), (5b)
4
3
where H spin-direction h-direction
ǫ (J J J′ )m +h/2
ǫx ≡ (J +−J⊥+−J⊥′ )mx J
ǫy ≡ (J +⊥J +⊥J′ )my +H/2 , (6) J⊥
ǫz ≡≡ (−ǫ2x+ǫ2y⊥+ǫ2z)1⊥/2 z my h = 0 hcritical h
and β and m are, respectively, the inverse temperature U(1) SSB phase Symmetric
phase
1 and the total magnetization per site. The numeri- degeneracy
kBT
cal solutions of Eq. (5b) are given in Fig. 2. They in-
dicate that there is a second-order phase transition, and FIG. 3: Variation of the spin configuration in a plaquette
whenthestaggeredfieldisincreasedgraduallyinthe2Dcom-
thecorrespondingorderparameteristhey componentof
the spin moment m = Sy . Going back to Fig. 1, petitivecase. Theblackarrowsrepresentspindirectionspro-
y |h i,j,ki| jectedontospinxy plane. Thegrayarrows arethestaggered
field h.
(a) (b)
0.5
m
x
m
y
ns mz
o
ati H Uniform Field
z
eti
gn 2(J+J ⊥ +J’⊥ )
a
M
Critical
Surface
SSB phase
0.0
Sy 0
0.0 0.5 k BT 1.0 1.50.0 0.5 k BT 1.0 1.5 2(J ⊥ +J’⊥ ) 1/2 (J+J⊥ +J⊥’ )
(c) (d)
0.5
h
Staggered Field k T
ns B
o
ati Temperature
z
eti
n
ag FIG. 4: Schematic mean-field phase diagram in the competi-
M
tivecase.
In the SSB phase, the relations m = h and
0.0 x 4(J⊥+J⊥′ )
m = H hold within the MFT. Inserting these
0.0 0.4 0.80.0 0.4 0.8 z 4(J+J⊥+J⊥′ )
h h intoEq.(5b)andtakingthelimitmy 0,weobtainthe
→
mean-field critical surface in the space (k T,H,h):
B
FIG. 2: Magnetization curves of the competitive case for
′ 1
(J,J⊥+J⊥,H)=(1,0.2,0.2). Theseareobtainedbythenu- h˜2+H˜2 = tanh2 β (J +J +J′ ) h˜2+H˜2 , (7)
merical iterative method for Eq. (5b). The upper two parts c c 4 c ⊥ ⊥ c c
(cid:26) q (cid:27)
(a) and (b) are in h = 0.05 and h = 0.35, respectively. The
lroewspeercttwivoelpy.arts(c) and(d)are inkBT =0.3 andkBT =0.7, where h˜c ≡ 4(J⊥h+cJ⊥′ ), H˜c ≡ 4(J+JH⊥c+J⊥′ ) and the sub-
script c represents critical values. It can be simplified in
the cases T =0, h=0 and H =0, respectively, as
oneseesthatthephasewithfinitem breaksthetransla-
y
tional symmetry in the weakly coupled direction. In the h˜2+H˜2 = 1
c c 4
sfoylmlomwientgry, wbreeackailnlgt)hipshpahsea.seTahsetohteheSrSpBha(sspe,onintawnehoicuhs  H˜c = 21tanh βc4Hc . (8)
the spins are aligned to the field with m = 0, will be  h˜ = 1tanh β (J +(cid:16)J +(cid:17)J′ )h˜
y c 2 c ⊥ ⊥ c
called as the symmetric phase. We emphasize that the
transition between these two phases occurs only in the Thus the mean-field pnhase diagram can boe represented
highdimensionalspinsystemsandinthe presenceofthe as Fig. 4. Using the critical condition, one can calculate
competition. From these results, we can illustrate the somecriticalexponentswithintheMFT.Nearthecritical
variation of the spin moment when the staggered field h surface in the SSB side, the order parameter, the off-
is increased gradually at small T and H with Fig. 3. diagonal uniform and staggered susceptibilities: χ
u
≡
4
∂my and χ ∂my behave , respectively,as m (A (a) (b)
∂H s ≡ ∂h y ∼ c− H H
A)β, χ (A A)γ and χ (A A)γ′ where A h=0
u c s c
∼ − − ∼ − − Para
standsforT,H orh. Thecriticalexponentβ isfoundto Paramagnetic
be the conventional mean-field value 1/2. On the other 2J Phase 2J
pcfhroaeonrnmpjdue,gtnbhadoetietcshutfilaγaenlraddtnaoadrsHdγi′MnatunFtrdhTnehsr,soetausanutndltdtota1hrb.udesT1cta/hhs2iees,.lwiasTthtbihecerehcaaimsrueedsaeniffnome-tfiryteehnlidest PhaseAntiferromag AF Sz
energy per site is given as netic Sx
H=0
ǫMFT = − J(m2x+m2y −m2z)+Hmz+hmx (J+|J⊥ |+|J’⊥ |) /2 kB T S2n,j,k S2n+1,j,k
n
+(J⊥+J⊥′ )(m2y −m2x−m2z) , (9) FIG. 5: (a) Schematic mean-field phase diagram of the non-
competitive case in h = 0. (b) the variation of the spin
o
moment when the uniform field is increased gradually in
From this, one can easily confirm that the critical expo-
h=T =0.
nent for the specific heat is zero.
Now, we turn to the non-competitive case. Because
ator c (c†) as follows:
of no competitions, no singular phenomena occur when
h = 0. Canting of the spins in zx plane lowers both the
6 i S(1 c†c)(c† c) i S(c† c)
inter-chain interactions and the Zeeman energies. Thus 2 − 2S − 2 −
the expectationvalue ofthe spin moments canbe put as S~HP = q S c†c   qS c†c ,
− ≈ −
 S(1 c†c)(c†+c)   S(c†+c) 
S~i,j,k MFT = ( 1)imx, 0, mz . (10)  q2 − 2S   q2 (12)
h i −
where S is the spin quantum number generalized from
(cid:0) (cid:1)
The MFT in this case gives the self-consistent equations S = 1/2 and the sign denotes the leading approxima-
mx(z) =(ǫ′x(z)/2ǫ′)tanh(βǫ′)whereǫ′x(z) ≡[(−)J+|J⊥|+ tion in the 1/S expan≈sion. The above HPT is useful if
J′ ]m +h(H)/2 andǫ′ (ǫ2+ǫ2)1/2. At h=0, the the spin points to the y direction in the classical ground
|sy⊥st|emxr(ezd)ucestoaconventi≡onalxAFmz agnetinauniform state,asthebosonsthenrepresentquantumfluctuations.
magnetic field. Hence, there must be a phase transition In the SSB phase, actually, a canting structure (4) is
which divides the AF and paramagnetic phases, charac- expectedintheclassicalgroundstate,whichisequivalent
terized by the order parameter m . The critical line is to the MFT atT =0. The cantedspinmomentsmay be
x
given by expressed by the angles (θ,φ) as
( 1)icosθsinφ
Hc = 1tanh β (J + J + J′ )Hc . (11) S~i,j,k =m ( 1−)i+j+kcosθcosφ . (13)
4J 2 c | ⊥| | ⊥| 4J h i  − sinθ 
(cid:26) (cid:27)
 
Thus in order to apply the HPT to the present case, we
Thephasediagramandthevariationofthespinmoment
use the representation
are drawn in Fig. 5. In the three-dimensional parameter
space(kBT,H,h),theAFphasegivesafirst-orderphase S~ R ( 1)i+j+kθ
transition plane. i,j,k → x − ×
(cid:16) (cid:17)
R ( 1)j+k( φ)+δ π S~ ,(14)
z i+j+k,odd HP
− −
(cid:16) (cid:17)
where the operator R (β) represents a rotation about α
III. LINEAR SPIN-WAVE APPROXIMATION α
axisbyangleβ. Theoperation(14)isdescribedinFig.6.
IN T =0
For the original spin model (3), these rotations corre-
spond to a unitary transformation. After these trans-
With the MFT described in the preceding section, we formations,the leading order terms in 1/S is retainedto
investigatetheeffectsofthequantumfluctuationsinboth giveasolvableHamiltonianwhichisquadraticinbosonic
thecompetitiveandthenon-competitivecases,atT =0. operators.
The standard linear spin-wave approximation, based on The canting angles of the classical ground state are
the Holstein-Primakoff transformation (HPT) (Ref. 25) given by minimizing the classical Hamiltonian, which is
is employed. The detailed results are given in Appendix equivalent to the MFT energy, Eq. (9). The canting an-
A. gles in the classical ground state are thus given as
FirstwediscusstheSSBphaseofthecompetitivecase,
cosφ sinθ = H ,
which is the main subject. In the HPT, we replace the cl cl 4S(J+J⊥+J⊥′) (15)
spin operator with a boson annihilation (creation) oper- sinφcl = 4S(J⊥h+J⊥′ ).
5
(a) z (b) z (a)H=0 1.5 ω (k x ,0) (b)H=0 1.5 ω (k x ,0)
S S h=0 h=0.05
1.0 1.0
Si=2m,i+j+k=2n
S2n,j,k π S2n+1,j,k 0.5 0.5
(2)θ θ ∆
h
Sx (1)φ Sy Sx Sy -(πc )H=-π0/ 2 1.50ω ( πk x/ 2 ,π) π (-dπ)H=-π0/. 22 1.50ω ( πk x/ 2 ,π) π
h=0 h=0
FIG. 6: Definitions of the canting parameter. In the SSB 1.0 1.0
phase, as in (a), each spin direction is given by two rota-
0.5 0.5
tions (1) R ( φ) and (2) R (θ) applied in this order to spin
z x
pointingtoy−direction. Inthesymmetricphaseorinthenon- ∆
H
competitive case, spins are canted in the zx plane as shown π π π π π π π π
- - / 2 0 / 2 - - / 2 0 / 2
in (b).
FIG.7: MagnondispersionsoftheSSBphaseinthe2Dcom-
For the resulting quadratic Hamiltonian Hˆ , we petitive case for (S,J,J⊥) = (1/2,1,0.1) and ax = ay = 1.
HP
perform a Fourier transformation (FT) c† = The gray circles represent thegapless points.
i,j,k
N−d/2 ei~k·~rc†, where N is the linear system size, d
~k ~k
is the dimension of the system, k (k <π/a ) and a the staggered field alone can open the gap, because the
P α | α| α α
are, respectively, the wave-number and the lattice con- ground state does not break any continuous symmetry
stantfortheα-direction. Afour-modeBogoliubovtrans- spontaneously. On the other hand, the system remains
formation (BT),26 which mixes c~k,c−~k,c~k−~π,c−~k−~π and gapless at~k =0 due to the NG mechanism if h=0 and
their Hermitian conjugates (~π (0,π/a ,π/a )), leads H is not too large. The h-induced gap is thus defined as
y z
≡
to the diagonalized form ∆˜ =ω˜(~k =~0).
h
Whiletheh-inducedgapisdefinedforbothcases,there
Hˆ = ω(~k)c˜†c˜ +const, (16)
HP ~k ~k is a characteristic difference in the h dependence of the
X~k gaps. In the limit of small h, ∆˜h h1/2 for the non-
∼
with a single band in the first Brillouin zone, where c˜~k competitive case, but ∆h ∼ h for the competitive case.
isthemagnonannihilationoperatorandthek direction In other words, one can say that the h-induced gap in
x
corresponds to the strongly AF one. The explicit results the competitive case opens more slowly than in the non-
on the dispersion ω(~k) are lengthy and thus are given in competitive case. This is naturally understood because
the competition between J (or J′ ) and h weakens the
Appendix A. Here we discuss physical implications of ⊥ ⊥
effect of the external symmetry breaking by h. It also
our results.
First, the obtained dispersion satisfies ω(~k) 0 for all implies that the ground state is more stable in the non-
≥ competitive case, against quantum and thermal fluctu-
values of parameters. This implies that the SSB phase,
ations. The opening gaps are drawn in Fig. 8. On the
which appears as the classical ground state, is stable
other hand, in the limit of small H, ∆ H. Similarly
againstquantumfluctuations,atleastinthelowestorder H
∼
to the case of ∆ , this may be interpreted as a result of
of1/S. Somerepresentativesofthedispersionareshown h
the competition between the uniform field and the AF
in Fig. 7. At zero field (H = h = 0), there are two gap-
less points ~k = (0,0,0) and ~k = (π/a ,π/a ,π/a ), couplings.
h H x y z
We expect the spin-wave theory for the gaps to be
with linear dispersions in the neighborhoods. Let us de-
fine ∆ = ω(~k ) and ∆ = ω(~k ). Since our results in qualitatively correct even for S = 1/2. As discussed in
h h H H AppendixA2,thespin-wavedispersionofthesymmetric
Appendix A1 indicates that ∆ (∆ ) is non-vanishing
h H phasecanbe obtainedbythe replacement(J , J′ )
goanply. wThheentrhue6=ex0ci(tHatio6=n0g)a,pw, neacmalellyi,ttahsehm(Hini)m-inudmuceexd- (−J⊥,−J⊥′ ) in the dispersion of the non|-c⊥o|m|pe⊥t|iti→ve
case.
citation energy, is given by ∆ = min(∆ ,∆ ). Thus
h H
Finallyletusdiscusstherelationofthepresentresults
the gap ∆ vanishes exactly as long as either h or H
to the spin-wave theory in the 1D model (J =J′ =0)
remains zero. This is contrasting to the S = 1/2 1D ⊥ ⊥
with the staggered field h discussed in Ref. 5. The spin-
HAF model, where the staggered field alone induces the
gap.27 The gapless excitations are identified as Nambu- wave dispersion ω˜(~k) for the non-competitive case does
Goldstone (NG) modes. Indeed, when either H or h is approach smoothly to the 1D dispersion [Eq. (3.11) in
zero, the Hamiltonian has a continuous U(1) symmetry, Ref. 5], when J⊥,J⊥′ → 0. On the other hand, the dis-
which is broken spontaneously in the SSB phase. persionω(~k)forthecompetitivecaseapparentlydoesnot
In the non-competitive case, the magnon dispersion reduce to the 1D one in the limit of J⊥,J⊥′ → 0. This
relationω˜(~k)isgiveninEq.(A20)inAppendixA2. Now is because ω(~k) is the dispersion of the magnon excita-
6
0.5 ~∆ is
h
Hˆ Hˆ +Nd(J +J′ )(m2 m2 m2),
→ j,k ⊥ ⊥ y − x− z
j,k
X
∆
h Hˆ = JS~ S~
j,k i,j,k i+1,j,k
·
i
X
0.1 −(−1)j+k[h′+2(J⊥+J⊥′ )my](−1)iSiy,j,k
[h 2(J +J′ )m ]( 1)iSx
0.02 0.1 − − ⊥ ⊥ x − i,j,k
[H 2(J +J′ )m ]Sz , (17)
− − ⊥ ⊥ z i,j,k
FIG. 8: ∆h and ∆˜h in the 2D case for (S,J,J⊥,H) = where we introduced an infinitesimal staggered field
(1/2,1,0.1,0). In the present case where H = 0, the gaps
have simple forms: ∆h = (1+J/J⊥)1/2h and ∆˜h = [1+ (−1)i+j+kh′ paralleltotheorderparameter. TheCMFT
h/(4SJ)]1/2√4SJh (see Appendix). requiresthatthe meanfieldsmx,y,z areequivalentto the
correspondingmomentsoftheeffectivechainHˆ . Ithas
j,k
the twoeffective staggeredfieldsh h 2(J +J′ )m
x ≡ − ⊥ ⊥ x
tInionfaicnt,thfoerSaSnBy pfihnaitsee,hw,htihcehSisSBabpsehnatseinisthreea1lDizemdo[adneld. atinvde uhnyifo≡rmhfi′ e+ld2H(Jz⊥≡+HJ⊥′−)m2y(Ja⊥s+weJl⊥′l)amsz.theCleeffaerlcy-
henceω(~k)isapplicable]onlywhenJ andJ′ areabove it is sufficient to consider one chain where j + k is
the criticalvalues. Thusbydecreasin⊥gJ (J′⊥)atafixed even, and we represent it as Hˆ1D. Within the linear-
⊥ ⊥ responsetheory,themoment Sy ,inwhich stands
h,the systemundergoesaphasetransitionintothe sym- |h ii| h···i
metricphase. Atthetransitionthedispersionshouldalso for the mean value of Hˆ1D, can be approximated by
change drastically. In the symmetric phase, similarly to χ1yD(Hz,hx,0)hy wherethestaggeredsusceptibilityisde-
the non-competitive case, the dispersion does approach fined as χ1D(H ,h ,h ) ∂|hSiyi|. Therefore the above
continuously to the 1D dispersion. y z x y ≡ ∂hy
requirement leads to m = χ1Dh which is transformed
y y y
to
IV. CHAIN MEAN-FIELD THEORY m = χ1yD h′. (18)
APPROACH y 1−2(J⊥+J⊥′ )χ1yD
Similarly m and m can be determined by the CMFT
In this section, we reconstruct the phase diagram of x z
as well. The critical condition of our model is
our model using chain mean-field theory (CMFT). In
theCMFT,weakcouplingsamongthechainsaretreated
1 2(J +J′ ) χ1D(H ,h ,0)=0. (19)
with a MFT, and the resulting effective 1D problem is − ⊥ ⊥ y z x
analyzed as precisely as possible. If the 1D problem can
Atthispoint,oneseesthattheoriginal3Dor2Dsuscep-
be treated exactly, the CMFT is expected to be much
tibilities and moments can be described by those of the
reliable when the one dimensionality is strong enoughas
effective chain.
in the case of Cu-benzoate, since it includes the fluctu-
The staggered field in Hˆ has both x and y com-
ations in the strongly coupled direction correctly. The 1D
ponents: h and h . By the infinitesimal rotation R (δ)
usefulness of the CMFT has been demonstrated in sev- x y z
eral applications.23,24,28 aboutz axisbyangleδ,wheresinδ =−[h2y/(h2y+h2x)]1/2,
the effective Hamiltonian is simplified as
In Sec. IVA, we discuss how the CMFT determines
the phase transition for our model (3). Sec. IVB is a
brief overview of susceptibilities of the S = 1/2 HAF Hˆ1′D = JS~i′·S~i′+1−HzSi′z −h′x(−1)iSi′x, (20)
chainwhicharenecessarytotheCMFT.InSec.IVC,we i
X
presenttheCMFTphasediagramsandcomparethemto
with the one-component staggered field h′ = h /cosδ.
the MFT ones. x x
Inordertoobtainanalternativeformuladeterminingm
y
instead of Eq. (18), we focus on the relation
A. CMFT for Our Model S′x ′ = cosδ Sx sinδ Sy
h i i h ii− h ii
= ( 1)i(cosδ m sinδ m ), (21)
Letusderivetheeffective1Dmodelforoursystem(3), x y
− −
within the CMFT.
In the competitive case, we consider the symmetric where h···i′ represents the expectation value of Hˆ1′D
phasesideforconvenience. Themean-fieldprocedurefor and the secondequality is caused by the self-consistency
the weak inter-chain couplings replaces them with the of the CMFT. Here we define the susceptibilities of
effective external fields. Thus the resulting Hamiltonian the HAF chain (20) as χ1uD(T,Hz,h′x) ≡ ∂∂mHz′z and
7
χ1sD(T,Hz,h′x) ≡ ∂∂mh′x′x where m′x,z = |hSi′x,zi′|. Within coorym2p9,a30c,t3i1ficaantdionthreasdpiuins-wofavteheveelffoeccittyiv.eTbhoesoenxaficetldvatluhees-
the linear-response theory Eq. (21) is reduced to
v(H) and R(H) as functions of the uniform field H are
χ1D(T,H ,h′) h′ =cosδ m sinδ m . (22) given by a solution of a set of the Bethe ansatz integral
s z x x x− y equations.32 In the case of H = 0, they are explicitly
Let us recall that δ is defined by m and m , and that given as
x y
m are determined by the CMFT. Consequently, m
x,z y
can be determined as a solution to Eq. (22). The condi- v =πJa/2, R=1/√2π. (24)
tion that m diverges would determine the phase transi-
y
tion.
For a small uniform field H =H( J), the asymptotic
z
behavior of the radius R follows5 ≪
B. Susceptibilities of S =1/2 AF chains 1
2πR2 1 . (25)
≈ − 2ln(J/H)
In order to solve Eqs. (19) or (22) in terms of
m , we need the explicit forms of the susceptibili-
y The logarithmic temperature correction due to the
ties: χ1D and χ1D. Here we briefly summarize the
u s marginal operator of the HAF chain is discussed in
known results5,29,30,31 on these quantities, obtained by Ref. 33. Although the transverse staggered field h′ in-
x
the bosonization technique. duces a gap, it is expected to have little effect1,5 on the
Intheabsenceofthestaggeredfieldh′x,thelow-energy uniform susceptibility χ1D if h′ is small enough.
u x
effectivetheoryofoftheHeisenbergchain(20)isgivenby
Next we turn to the staggered susceptibility χ1D. In
a free boson field theory, and the uniform susceptibility s
the caseJ h′, k T,the low-energyeffective theoryof
at zero temperature is obtained as ≫ x B
theHamiltonian(20)isgivenbyaquantumsine-Gordon
a fieldtheory. Usingthe exactsolutionsofthe HAF chain,
χ1D(T,H,0) , (23)
u ≈ (2π)2R(H)2v(H) thescalingargumentsandLukyanov-Zamolodchikovpre-
diction34,35, the staggered susceptibility χ1D for small
s
where H = H, and R and v, respectively, are the H =H and h′ =h at T =01,5 is given as
z z x
D[2(1 2πR2)]−1/3 πR2 J −2(1−2πR2)/3 h πR2/(2−πR2) h−1 (H h)
− 2−πR2 H J ≫
χ1sD ≈ DD2e1−/31/3h31lnlnJHJ 1/13/3h−Jh1 1/(cid:0)3 h(cid:1)−1 (cid:0) (cid:1) ((HJ ≫=H0)≫h) , (26)
34/3 J (cid:2) (cid:0)h (cid:1)(cid:3) (cid:0) (cid:1)
 (cid:2) (cid:0) (cid:1)(cid:3)
where the radius R is that of the model without the C. Phase diagrams in CMFT
staggered field, and D 0.3868.... The first formula
≡
is actually valid for H 2J (below saturation field), EmployingtheresultsofSecs.IVAandIVB,westudy
≤
but the second is only so for H J. These formulas the phase diagrams, in particular for the competitive
≪
are correct in kBT h J. (More precisely, within case,withinthe CMFT.Unfortunately,itcanbe applied
≪ ≪
kBT ∆h J where ∆h is the h-induced gap in the only to several limited regions in the parameter space,
≪ ≪
HAF chain.5) where the susceptibilities of the 1D model are obtained
exactly.
In the intermediate temperature regime h,H
≪ First, let us consider the region near (kBTc,0,0). In
dkBucTed≪gaJp,,wthheersetatghgeerteedmpsuesrcaetputriebiilsitlyarmgearytbheanaptphreoixni-- the zero-field case, the effective model Hˆ1D has only an
infinitesimal staggered mean field h as long as it is in
mated by that for zero staggered field5 as y
the symmetric phase. Therefore the formula (27) can
give the self-consistent value of m , and Eq. (19) is the
y
critical condition which serves the critical temperature:
[ln(J/k T)]1/2
χ1sD(kBT ≫h) ≈ D kBBT , (27) kBTc = 2D (J⊥+J⊥′ ) ln kBJTc 1/2 (28)
h (cid:16) (cid:17)i 1/2
2 (J +J′ ) ln J ,
≈ D ⊥ ⊥ 2D (J⊥+J⊥′ )
h (cid:16) (cid:17)i
where 0.2779.... which is reasonable when k T , (J + J′ ) J and
D≡ B c ⊥ ⊥ ≪
8
0.8 kB Tc H=h=0 (a) 0.8 kB Tc symmetric phase CombiningEqs.(30)and(31),weobtainthecriticalstag-
gered field:
symmetric phase SSB phase h = D′ J⊥+J⊥′ ln 5J 1/22(J +J′ )
c J 2hc ⊥ ⊥
SSB phase H=h=0 (b) D′hJ⊥+J⊥′ ln(cid:16) 5(cid:17)i J 1/2 1/2 (32)
0 J⊥ + J⊥’ 0.3 0 J⊥ + J⊥’ 0.3 ≈ 2((cid:20)J J+J′ ),(cid:18)4D′ (cid:16)J⊥+J⊥′ (cid:17) (cid:19)(cid:21)
Chain Mean-Field Theory Mean-Field Theory × ⊥ ⊥
wherewekeptonlytheleadingorderof(J +J′ )/J and
⊥ ⊥
FIG. 9: (kBTc,J⊥ +J⊥′ ) in the competitive case for J = 1. D′ (2 102D33−7)1/2 7.27 10−2. This is valid
(a)and(b)are,respectively,predictedwithintheCMFTand ifh≡, (J×+J′ ) J,and≈iscom·p·a·r×edtotheMFTresult
the MFT. It is confirmed that the SSB areas of the CMFT h =c 2(J⊥ +⊥J′ )≪extracted from Eq. (8) in Fig. 10. The
c ⊥ ⊥
are considerably smaller than theMFT. CMFT correction to the MFT is found as a significant
multiplicative factor D′[ ]1/2.
···
0.1 hc H=T=0 (a) 0.1 hc symmetric phase We consider furthermore the critical line in the T =0
plane in the limit of h H J. In the sym-
c c
metric phase near this lin≪e, the ≪effective model Hˆ
symmetric phase 1D
SSB phase has all three kinds of the external fields. Hence mx
and m must be determined concurrently by the CMFT
H=T=0 (b) z
SSB phase scheme. However in the present case hc Hc, mx may
≪
be estimated independently by taking an approximation
0 0.3 0 0.3
J⊥ + J⊥’ J⊥ + J⊥’ χ1D(0,H,h) χ1D(0,H,0) which was given in Eq. (23).
Chain Mean-Field Theory Mean-Field Theory Fruom this ap∼proxuimation, m is also fixed as
z
′ H
(FaI)Ga.n1d0(:b)(hacr,eJ,⊥re+speJc⊥ti)veinly,tphreedcoicmtepdetwitiitvheinctahseeCfoMrFJT=an1d. mz ≈ π2J(1−[ln(J/H)]−1)+2(J⊥+J⊥′ ), (33)
theMFT.SimilarlytoFig.9,thenarrowingoftheSSBareas
occurs. whichisjustifiedinH, (J⊥+J⊥′ )≪J. Inthesufficiently
small field case, J H( h), the logarithmic part can
≫ ≫
be dropped as well. From the second of Eq. (26) and
agrees with the result of Ref. 24. Equation (28) is also Eqs. (30), (31) and (33), we obtain the critical line in
stable against a small staggered field h, because χ1D is T =0
s
independent of h in Eq. (27). These results are also
valid for the non-competitive case, with the replacement h = D′′ J⊥+J⊥′ ln π2J(1−[ln(J/Hc)]−1)+2(J⊥+J⊥′ )
J +J′ J + J′ . Figure 9 represents the compar- c J π2Hc
⊥ ⊥ →| ⊥| | ⊥| h (cid:16) (cid:16) 1/2 (cid:17)
ison between the CMFT result (28) and the mean-field +[ln(J/H )]−1+ 2(J +J′ ), (34)
prediction: k T =(J +J +J′ )/2. c ··· ⊥ ⊥
B c ⊥ ⊥ (cid:17)i
Next we investigate the neighborhood of (0,0,h ). In
c where D′′ (102D3e−13−6)1/2 5.40 10−2. This
this case (H =0), Hˆ has two staggered fields. There- ≡ ≈ ···×
1D conditionispresumablysuitablefork T h H
B c c c
fore through the rotation of Sec. IVB, the order param- ≪ ≪ ≪
J. Thus, in order to obtain a more precise condition, it
eter m can be fixed by Eq. (22). Inserting the third
y isnecessarytoadoptthe firstformula(26)andthe exact
formula of Eq. (26) into Eq. (22), and performing the
values of R and v. Figure 11 exhibits the comparison
Taylor expansion of Eq. (26) around h = 0, we obtain
y between this line and the mean-field prediction.
the linear-response relation: Finally, we consider the point (0,H ,0), where Hˆ
c 1D
has only the uniform field H = H 2(J + J′ )m
my = h−13{1{032(J−⊥16+[lJn⊥′(J)/−h[lxn)(]J−/1h}xm)]x−1}mx h′. (29) efrxocmeptBefotrhethaensinafitznittheasitmtahlefimezldaghnye.tizcIat−thioans sb⊥aeteunrakt⊥neoswanzt
the point H = 2J at T = 0 in the HAF chain having
Therefore the critical condition can be written as z
only the field H . The transition point between the SSB
z
3hc and symmetric phase in this case should be identified
m , (30)
x ≈ 10(J +J′ ) withthesaturationoftheuniformmagnetization. Hence,
⊥ ⊥
within the CMFT, the critical uniform field is given as
where we assumed h , (J + J′ ) J. On the other
hand,mx shouldbeficxedf⊥romth⊥es≪elf-consistencyofthe Hc = 2J +(J⊥+J⊥′ ). (35)
CMFT as well. At T =0, it leads to
The substitution J + J′ (J + J′ ) gives the
⊥ ⊥ → − | ⊥| | ⊥|
m = χ1sD(0,0,h−2(J⊥+J⊥′ )mx) h. (31) critical field of the AF-paramagnetic transition in the
x 1+2(J⊥+J⊥′ )χ1sD(0,0,h−2(J⊥+J⊥′ )mx) non-competitive case.
9
Chain Mean-Field Theory H
0.025
h symmetric phase
c
0.005
SSB
0.2
SSB phase 0.1 H0.1 phase k B T
c
J⊥ + J’⊥ 0.3 critical surface in CMFT
Mean-Field Theory
critical surface in MFT
h
h symmetric phase
c
0.1
symmetric phase
FIG. 12: Schematic phase diagrams of the CMFT and the
MFT in thecompetitive case.
0.025
0.2
0.1
SSB phase 0.1 depending on whether the staggered field and the inter-
H
J⊥ + J’⊥ 0.3 c chain couplings are competitive or not. In the com-
petitive case, the appearance of a characteristic ordered
(SSB) phase is predicted by the MFT. The SSB phase
FIG. 11: Critical surface (h ,H ) in the competitive case for
c c breaksthetranslationalsymmetryoftheweaklycoupled
(J,T) = (1,0) obtained with the CMFT (34) (upper panel)
direction,andthereforeitispeculiartohighdimensional
and the MFT (8) (lower panel). In the whole region of the
systems. We also applied the CMFT to the model (3),
CMFT panel, the critical region surrounded by the dashed
ring (h H J) is greatly reliable. and predicted that the region of the SSB phase becomes
c c
≪ ≪ narrowin the CMFT scheme. The MFT and the CMFT
arevalid,respectively,inJ J ,J′ andinJ J ,J′ .
∼ ⊥ ⊥ ≫ ⊥ ⊥
Fromtheseresults,wecancomparetheCMFTandthe The crossover behavior between these two regions can
MFT phase diagrams. The comparison for the compet- notbedescribedbythemean-fieldtypeapproach.36,37,38
itive case is summarized in Fig. 12. In the case of weak Itwouldrequireamoreprecisetreatmentoffluctuations.
inter-chaincouplings(J J ,J′ ),theSSBphaseofthe Moreoverwestudiedspin-wavetheoryinboththecom-
≫ ⊥ ⊥
CMFT is much smaller thanone ofthe MFT. Especially petitive and non-competitive cases at T = 0. When
there is a significant narrowing in k T and h directions. the uniform field H is non-vanishing, the h-induced gap
B
As seen from Eq. (18), this is because the phase transi- opens as ∆ h in the SSB phase, while ∆˜ h1/2
h h
∼ ∼
tioninthe CMFT frameworkisdrivenbythe divergence in the AF phase of the non-competitive case. This dif-
of the susceptibility (in the present case, χ1D) in the ef- ference reflects the partial cancellation of the staggered
s
fectivechain,whiletemperatureandthefieldh (orm ) field effect due to the competitive inter-chaininteraction
x x
suppress the divergence. On the other hand, the reduc- in the SSB phase. The spin-wave dispersion in the SSB
tionofthecriticaluniformfieldH issmallintheweakly phase remainsgaplessdue to NG mechanismevenunder
c
coupledcase. This is becausethe uniformfieldcompetes a non-vanishing h. This is in contrast to the case of the
with the intra-chain AF interaction as well as with the 1D model.
inter-chain interactions. Finally we comment on a few recent reports related
Finallywereviewthevalidityofthetwotheories. Since to our study. In BaCu Si O reported in Ref. 39, both
2 2 7
the strong one dimensionality is the basis of the CMFT the staggered field and the inter-chain interactions are
procedure,itisexpectedthatthe CMFTismorereliable expected, as in our models. However, the effect of the
Jin⊥thanedlimJ⊥′itaorfeJco≫mpJa⊥ra,bJl⊥′e.toOJn,tthheeostpheecriahlatnrdea,twmheennt epxacphearn,giseaarngiusoedtrotpoiebse, rwehspicohnsiisbliegnfoorretdheinobtsheervperdestewnot
of only one direction is unjustified. Therefore the MFT, spin-floptransitions. Extendingthepresentworktosuch
which treats all couplings equally, is more reasonablefor a system would be an interesting problem in the future.
J ∼J⊥,J⊥′ . Furthermore, in BaCu2(Si1−xGex)2O7,22 the sign of the
inter-chain interaction seems to depend on the doping
parameter x. Thus, it could provide a realization of the
V. SUMMARY AND DISCUSSION competitive and non-competitive cases.
Wang et al.2 investigated an S = 1/2 AF ladder sys-
We considered the effects of the staggered field h in temwithastaggeredfield. Theyarguethatthecompeti-
an S = 1/2 Heisenberg antiferromagnet (3) in two or tionbetweenthestaggeredfieldandtherunginteraction
three dimensions. The system behaves quite differently brings a quantum criticality. It might be interesting to
10
compare our analysis on the higher dimensional system where and T, respectively, stand for the complex con-
∗
with theirs. jugate of each matrix component and the transpose of
matrices, and the 4 4 matrices ξ , η and the column
× ~k ~k
four-vector are given as
C~k
Acknowledgements
We thank Collin Broholm, Dan Reich and Hidekazu
Tanaka for useful comments. This work was partially
supported by Grant-in-Aid by MEXT of Japan.
E (~k) 0 0 iE (k )
APPENDIX A: DETAILS OF SPIN-WAVE 1 4 y,z
RESULTS IN SEC. III ξ~k =  00 iEE1((~kk) ) iEF4((k~ky),z) 00 ,
4 y,z 1
−
Here we supplement the spin-wave results omitted in  iE4(ky,z) 0 0 F1(~k) 
−
Sec. III.  0 E (~k) 0 iE (k ) 
2 3 x
E (~k) 0 iE (k ) 0
1. The competitive case η~k =  20 iE3(kx) 30 x F2(~k) ,
iE (k ) 0 F (~k) 0 
 3 x 2 
 
Wewritedownthedetailsofthecompetitivecase. Af- T
= c c c c . (A2)
ter the FT of the boson operator c , the spin-wave C~k ~k −~k ~k−~π −~k−~π
i,j,k
Hamiltonian can be expressed as the following matrix (cid:0) (cid:1)
form:
HˆHP = X~k (cid:16) C~k†T C~kT (cid:17)(cid:18)ηξ~~kk∗ ηξ~~kk∗ (cid:19)(cid:18)CC~~kk† (cid:19)−4E1(~k)
+Ecl, (A1) Here E are defined as
gs 1,2,3,4
E (~k) = 2SJ(1 2sin2θ cos2φ )+2S(J +J′ )(2cos2θ cos2φ 1) 2SJsin2θ cos2φ cosk a
1 − cl cl ⊥ ⊥ cl cl− − cl cl x x
h
+2S(cos2θ (1+sin2φ ) 1)(J cosk a +J′ cosk a )+Hsinθ cosφ +hsinφ /8,
cl cl − ⊥ y y ⊥ z z cl cl cl
i
E (~k) = SJ(cos2θ sin2θ sin2φ )cosk a +Scos2θ cos2φ (J cosk a +J′ cosk a ) /4,
2 cl− cl cl x x cl cl ⊥ y y ⊥ z z
E (k ) = h SJsin2θ sinφ cosk a /4, i
3 x cl cl x x
−
E (k ) = Ssin2θ sinφ (J cosk a +J′ cosk a )/4, (A3)
4 y,z cl cl ⊥ y y ⊥ z z
and F (~k)=E (~k ~π). Thus ξ is Hermitian and η where Ω = diag(ω (~k),ω (~k),ω (~k),ω (~k)). According
1,2 1,2 − ~k ~k ~k 1 2 3 4
is symmetric. Let us suppose that a four-mode BT to Ref. 26, determining Ω and M (~k) is equivalent to
~k BT
solving an eigenvalue problem
˜
CC˜~~kk† !=MBT(~k)(cid:18)CC~~kk† (cid:19), (A4) (cid:18)ηξ~~kk∗ −−ηξ~~kk∗ (cid:19)MB†T = MB†T(cid:18)Ω0~k −0Ω~k (cid:19). (A6)
wsohner(emaC˜~gkn=on)(c˜o~kp,ec˜r−a~kt,oc˜r~ks−a~πn,dc˜−M~k−B~πT)(T~k)isisaanse8t of8nmewatrbiox-, T±hλel (elig=ht1e,i2g,e3n,v4a)l,uwesh±erωej(~k) (j =1,2,3,4)are givenby
×
diagonalizes the Hamiltonian as follows: λ (~k) = [1/2G 1/2(G2 4G+)1/2]1/2,
1 ~k− ~k− ~k
Hˆ = ˜†T ˜T Ω~k 0 C˜~k 4E (~k) λ2(~k) = [1/2G~k−1/2(G~2k−4G~−k)1/2]1/2,
HP X~k (cid:16)C~k C~k (cid:17)(cid:18) 0 Ω~k (cid:19) C˜~k† !− 1 λ3(~k) = [1/2G~k+1/2(G~2k−4G~+k)1/2]1/2,
+Egcsl, (A5) λ4(~k) = [1/2G~k+1/2(G~2k−4G~−k)1/2]1/2, (A7)