Clustering of Sloan Digital Sky Survey III Photometric Luminous Galaxies: The Measurement, Systematics and Cosmological Implications

4.7 MB·English

by  Shirley Ho

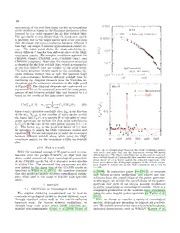
Draft version January 11, 2012
PreprinttypesetusingLATEXstyleemulateapjv.5/2/11
CLUSTERING OF SLOAN DIGITAL SKY SURVEY III PHOTOMETRIC LUMINOUS GALAXIES: THE
MEASUREMENT, SYSTEMATICS AND COSMOLOGICAL IMPLICATIONS
Shirley Ho1,2,3, Antonio Cuesta4, Hee-Jong Seo5, Roland de Putter6,7, Ashley J. Ross8, Martin White1,9,10,
Nikhil Padmanabhan4, Shun Saito10, David J. Schlegel1, Eddie Schlafly11, Uros Seljak1,9,10,12,13, Carlos
Hernández-Monteagudo14,26, Ariel G. Sánchez15, Will J. Percival8 Michael Blanton16, Ramin Skibba17 Don
Schneider 27,28 Beth Reid1,29 Olga Mena7, Matteo Viel19,20 Daniel J. Eisenstein 11 Francisco Prada21
Benjamin Weaver16 Neta Bahcall22 Dimitry Bizyaev 23 Howard Brewinton 23 Jon Brinkman23 Luiz Nicolaci
2 da Costa24,25 John R. Gott 22 Elena Malanushenko 23 Viktor Malanushenko 23 Bob Nichol 8 Daniel
1 Oravetz 23 Kaike Pan 23 Nathalie Palanque-Delabrouille 30 Nicholas P Ross 1 Audrey Simmons 23 Fernando
0 de Simoni24,25,31 Stephanie Snedden 23 Christophe Yeche 30
2 (Dated: January 11, 2012)
Draft version January 11, 2012
n
a ABSTRACT
J
The Sloan Digital Sky Survey (SDSS) surveyed 14,555 square degrees, and delivered over a trillion
0
pixels of imaging data. We present a study of galaxy clustering using 900,000 luminous galaxies with
1
photometric redshifts, spanning between z = 0.45 and z = 0.65, constructed from the SDSS using

methods described in Ross et al. (2011). This data-set spans 11,000 square degrees and probes a
]
O volume of 3h−3Gpc3, making it the largest volume ever used for galaxy clustering measurements. We
C describeindetailtheconstructionofthesurveywindowfunctionandvarioussystematicsaffectingour
measurement. Withsuchalargevolume,highprecisioncosmologicalconstraintscanbeobtainedgiven
.
h acarefulcontrolandunderstandingoftheobservationalsystematics. Wepresentanoveltreatmentof
p the observational systematics and its applications to the clustering signals from the data set. In this
- paper,wemeasuretheangularclusteringusinganoptimalquadraticestimatorat4redshiftsliceswith
o
an accuracy of ∼ 15% with bin size of δ = 10 on scales of the Baryon Acoustic Oscillations (BAO)
r l
t (at (cid:96) ∼ 40−400 ). We also apply corrections to the power-spectra due to systematics, and derive
s
cosmological constraints using the full-shape of the power-spectra. For a flat ΛCDM model, when
a
[ combined with Cosmic Microwave Background Wilkinson Microwave Anisotropy Probe 7 (WMAP7)
andH constraintsfromusing600CepheidsobservedbyWideFeildCamera3(WFC3)(HST),wefind
0
1 Ω =0.73±0.019 and H to be 70.5±1.6 s−1Mpc−1km. For an open ΛCDM model, when combined
v Λ 0
with WMAP7 + HST, we find Ω = 0.0035±0.0054, improved over WMAP7+HST alone by 40%.
7 K
For a wCDM model, when combined with WMAP7+HST+SN, we find w =−1.071±0.078, and H
3 0
to be 71.3±1.7 s−1Mpc−1km, which is competitive with the latest large scale structure constraints
1
2 fromlargespectroscopicsurveyssuchasSDSSDataRelease7(DR7)(Reidetal. 2010, Percivaletal.
. 2010,Montesanoetal. 2011)andWiggleZ(Blakeetal. 2011). Wealsofindthatsystematic-corrected
1
power-spectragivesconsistentconstraintsoncosmologicalmodelswhencomparedwithpre-systematic
0
correction power-spectra in the angular scales of interest. The SDSS-III Data Release 8 (SDSS-III
2
DR8) Angular Clustering Data allows a wide range of investigations into the cosmological model,
1
cosmic expansion (via BAO), Gaussianity of initial conditions and neutrino masses. Here, we refer
:
v to our companion papers (Seo et al. 2011, de Putter et al. 2011) for further investigations using the
i clustering data. Our calculation of survey selection function, systematics maps, likelihood function
X
for COSMOMC package will be released at http://portal.nersc.gov/project/boss/galaxy/photoz/.
r
a
1Lawrence Berkeley National Laboratory, 1 Cyclotron Rd, CSIC,Spain
MS50R-5045,Berkeley,CA94720,USA 8Institute of Cosmology & Gravitation, Dennis Sciama
2Carnegie Mellon University, Physics Department, 5000 Building,UniversityofPortsmouth,PortsmouthPO13FX,UK
ForbesAve,Pittsburgh,PA15213,USA 9Department of Physics,University of California Berkeley,
[email protected] Berkeley,CA
4Yale Center for Astronomy and Astrophysics, Yale Univer- 10Department of Astronomy, University of California Berke-
sity,NewHaven,CT06511,USA ley,CA
5BerkeleyCenterforCosmologicalPhysics,LBLandDepart- 11Department of Astronomy, Harvard University, 60 Garden
ment of Physics, University of California, Berkeley, CA 94720, St. MS20,CambridgeMA02138
USA 12Institute for Theoretical Physics, University of
6ICC, University of Barcelona (IEEC-UB), Marti i Franques Zurich,Winterthurerstrasse 190, CH-8057 Zurich, Switzer-
1,Barcelona08028,Spain land
7Instituto de Fisica Corpuscular, Universidad de Valencia- 13EwhaUniversity,Seoul120-750,Korea
2
1. INTRODUCTION Micron All sky Survey (2MASS, Skrutskie et al. 2006),
COSMOS (Scoville et al. 2007), Canada-France-Hawaii
The distribution of light in the Universe has long been
used as a probe into the structure of the Universe. Ein- TelescopeLegacySurvey34 (CFHTLS,Ilbertetal.2006),
stein wrote of the distribution of stars as possibly being Galaxy And Mass Assembly survey (GAMA, Driver et
uniform on average over large enough distances in 1917 al. 2009), The WiggleZ Survey (Blake et al. 2010), the
whenhediscussedthestructureoftheUniverse. Hubble Sloan Digital Sky Survey (SDSS, York et al. 2000). By
tested the uniformity of distribution of faint nebulae in 2008, the SDSS35 has probed ∼ 1.5 Gpc3 with galaxies,
1926. As the structure of the Universe unfolds, distribu- while the current SDSS-III(Eisenstein et al. 2011) will
tionoflightfromobjectssuchasgalaxieshasremaineda finish surveying ∼ 15 Gpc3 in 2014. The planned Large
powerful cosmological probe (Peebles 1973; Groth 1973; SynopticSurveyTelescope(LSST)36 willobserve∼1000
Wang et al. 1999; Hu 1999; Eisenstein et al. 1999). Gpc3 of the Universe.
Smoothed over large scales, we expect galaxy density Hidden in the ever-increasing volume of surveyed Uni-
to have a simple relationship to the underlying matter verse, isthewealthofcosmologicalinformationthathad
density; this implies that the clustering of galaxies at not been fully exploited. In particular, the large scale
largescalesisdirectlyrelatedtotheclusteringoftheun- clustering of any mass tracer, usually characterized by
derlying matter and is thus a sensitive probe of both the its power-spectrum, in the Universe contains three fea-
initialconditionsoftheUniverseanditssubsequentevo- turesthatareofsignificantinteresttocontemporarycos-
lution. It is therefore not surprising that a large fraction mologists. The first distinguishing feature is oscillations
oftheeffortinobservationalcosmologyhadbeendevoted in the power-spectrum caused by acoustic waves in the
to measuring the spatial distribution of galaxies, as in baryon-photonplasmabeforehydrogenrecombinationat
the CfA Redshift Survey (Huchra et al. 1983),The APM z ∼1000, called Baryon Acoustic Oscillations (hereafter
Galaxy Survey (APM, Maddox et al. 1990), The DEEP BAO) (Peebles & Yu 1970; Sunyaev & Zeldovich 1970;
survey33 (DEEP, Koo 1998), VIMOS-VLT Deep Survey Bond & Efstathiou 1984; Holtzman 1989; Hu & White
(VVDS, Le Fèvre et al. 2005), Two-Degree Field Galaxy 1996; Eisenstein & Hu 1998). The BAO technique has
Redshift Survey (2dFGRS, Cole et al. 2005),The Two emerged as the new precision cosmology probe, espe-
cially in discerning the properties of this unknown dark
14Centro de Estudios de Física del Cosmos de Aragón component of the Universe "Dark Energy". The BAO
(CEFCA), Plaza de San Juan 1, planta 2, E-44001, Teruel, was first observed in early 2005 both in the SDSS Lu-
Spain
minous Red Galaxy sample (Eisenstein et al. 2005), the
15Max-Planck-InstitutfürExtraterrestrischePhysik,Giessen-
bachstrasse1,85748Garching,Germany 2dFGRS data (Cole et al. 2005) and in 2006 by using
16Center for Cosmology and Particle Physics,Department of photometric Luminous Galaxies (LRGs) in 3500 deg2 of
Physics,New York University,4 Washington Place, New York,
SDSS (Padmanabhan et al. 2007). However, neither of
NJ10003,USA
17StewardObservatory,UniversityofArizona,933N.Cherry thesignalswerestrongenoughtoplacestrongcosmologi-
Avenue,Tucson,AZ85721,USA calconstraintsviaBAO.Second,thelargestscalesofthe
18Instituto de Fisica Corpuscular (IFIC), Universidad de power-spectrum can be used to constrain the primordial
Valencia-CSIC,Spain
potential of the Universe, thus testing inflation. In par-
19INAF - Osservatorio Astronomico di Trieste, Via G.B.
Tiepolo11,I-34131Trieste,Italy ticular, Dalal et al. (2008) has pointed out the relation-
20INFN/National Institute for Nuclear Physics, Via Valerio shipbetweennon-gaussianityofthepotentialintheearly
2,I-34127Trieste,Italy Universe (due to various possible inflationary scenarios)
20Instituto de Fisica Corpuscular (IFIC), Universidad de
and the large scale power of mass tracer in the Universe.
Valencia-CSIC,Spain
21Instituto de Astrofísica de Andalucía (CSIC), E-18080 Finally, at k ∼ 0.01hMpc−1, the power spectrum turns
Granada,Spain over from a k1 slope (for a scale invariant spectrum of
22Astrophysical Science, Princeton University, Princeton,
initialfluctuations),toak−3 spectrum,causedbymodes
NJ08544
23Apache Point Observatory, P. O. Box 59, Sunspot, that entered the horizon during radiation-dominated era
NM88349-0059 and were therefore suppressed. The precise position of
24Laboratório Interinstitucional de e-Astronomia - LIneA,
thisturnoveristhusdeterminedbythesizeofthehorizon
RuaGal. JoséCristino77,RiodeJaneiro,RJ20921-400,Brazil
25Observatório Nacional, Rua Gal. José Cristino 77, Rio de at matter-radiation equality. It corresponds to a physi-
Janeiro,RJ20921-400,Brazil cal scale determined by the total matter (Ω h2) densi-
M
26Max-Planck-Institut für Astrophysik, Karl-Schwarzschild tiesandradiationdensities(Ω h2). Inparticular, witha
Str. 1,D-85748Garching,Germany γ
27DepartmentofAstronomyandAstrophysics,ThePennsyl- large survey such as SDSS, various groups had used the
vaniaStateUniversity,UniversityPark,PA16802 large scale power-spectrum to put stringent constraints
28Institute for Gravitation and the Cosmos, The Pennsylva- on cosmological parameters, most notably Zehavi et al.
niaStateUniversity,UniversityPark,PA16802
(2002); Tegmark et al. (2004); Eisenstein et al. (2005);
29HubbleFellow
30CEA, Centre de Saclay, IRFU, 91191 Gif-sur-Yvette, Padmanabhan et al. (2007); Percival et al. (2010); Reid
France
31Departamento de Física e Matemática,
PURO/Universidade Federal Fluminense, Rua Recife s/n, 34 http://www.cfht.hawaii.edu/Science/
JardimBelaVista,RiodasOstras,RJ28890-000,Brasil 35 www.sdss.org
33 http://deep.berkeley.edu/ 36 http://www.lsst.org
3
et al. (2010). of the sky using the dedicated Sloan Foundation 2.5 m
TheSDSShasnowsurveyed14,555deg2,andwithap- telescope located at Apache Point Observatory in New
propriatephotometricselection,wecanconstructalarge Mexico (Gunn et al. 2006). A drift-scanning mosaic
uniformsampleofthephotometricluminousredgalaxies CCD camera (Gunn et al. 1998; Gunn et al. 2006) im-
(Ross et al. 2011), and their photometric redshifts that aged the sky in five photometric band-passes (Fukugita
can be easilycalibrated using the acquired spectroscopic et al. 1996; Smith et al. 2002) to a limiting magnitude
redshifts of a uniform sub-sample (∼ 10%) of the pho- of r(cid:39) 22.5. The imaging data were processed through
tometric galaxies. This approach allows the possibility a series of pipelines that perform astrometric calibration
of using both standard rulers (from the turn over scale (Pier et al. 2003), photometric reduction (Lupton et al.
of power spectrum, and also the baryon acoustic oscilla- 2001) and photometric calibration (Padmanabhan et al.
tions) to acquire cosmological constraints. 2008). In particular, Baryon Oscillations Spectroscopic
We make use of this opportunity to derive one of Survey (hereafter BOSS) which is a part of SDSS III
the most accurate measurements of the galaxy angu- (Eisenstein et al. 2011; Aihara et al. 2011), has com-
lar power-spectra achieved to date. We start with the pleted an additional 3000 square degrees of imaging and
five band imaging of the SDSS-III DR8; Aihara et al. is now obtaining spectra of a selected subset of 1.5 mil-
(2011); Eisenstein et al. (2011)), and photometrically lion galaxies. The targets are assigned to spectroscopic
select a sample of luminous red galaxies, following the plates(tiles)usinganadaptivetilingalgorithmbasedon
CMASS galaxy selection detailed in White et al. (2011); Blanton et al. (2003), and observed with a pair of fiber-
thedetailsoftheconstructionofthesampleandthered- fed spectrographs.
shift distribution is described in Ross et al. (2011). We The availability of large uniform photometric data-set
then measure the angular clustering power spectra as a prompted the start of this project, thus a series of pa-
functionofredshiftwithanoptimalquadraticestimator, pers,startingwiththegenerationofthephotometricred-
which is proved to provide the best statistical error-bar shiftscatalogbyRossetal.(2011),whichuses112,778of
when the field is Gaussian. The galaxy density field is BOSS spectra as a training sample for photometric cat-
notGaussianonsmallscales,duetonon-linearevolution; alog. The photometric redshift catalog contains over 1.6
however, at relatively large scales, which are the scales million objects, and 900,000 of these objects lie within
weareconcernedhere, thefieldisclosetoGaussian. We our imaging mask and the selected redshift range (0.45
willdiscussthisissueindetailinthepaper. Withsucha < z < 0.65). The redshift range is selected so that it
large volume of data, we realize that the effects of large is nearly completely independent from DR7 analysis of
scale systematics are not negligible. To gauge and cor- LRGclusteringusingspectroscopywhichstopsatz ∼0.4
rect the effects of large scale systematics, we develop a (Reid et al. 2010; Percival et al. 2010); this allows for
novel method in correcting the large scale systematics possibility of trivial combination of likelihoods. These
given that we know the list of possible systematics. We galaxies are among the most luminous galaxies in the
construct the maps of various systematics, and calcu- universeandtracealargecosmologicalvolumewhilehav-
late their cross-correlation with the galaxy density, the ing high enough number density to ensure shot-noise is
systematic auto-correlations and cross-correlations. We not a dominant contributor to the clustering variance.
can then correct for these systematics applying this new The majority of the galaxies have spectral energy distri-
method. butions (∼ 85% , see Masters et al. (2011) and private
The paper is organized as follows : Sec. 2 describes communication with the BOSS galaxy-evolution group)
the construction of the sample; Sec. 3 then presents the that are distinctive of old stellar populations.
theory and measurement of the angular power spectra;
Sec. 4 discusses the various potential systematics and 2.2. Defining Luminous Red Galaxies
the novel method applied in correcting for the observa-
WemakeuseoftheCMASSsamplefromBOSS,which
tional systematics. Sec. 6.1 describes the validation of
is defined in White et al. (2011) and Ross et al. (2011);
the cosmological parameter fitting method, and Sec. 7
and we write down the criteria here again for conve-
summarizesthecosmologicalconstraintsthemselves. We
nience:
conclude in Sec. 8.
Wherever not explicitly mentioned, we assume best fit 17.5<i <19.9
cmod
WMAP7 (Larson et al. 2011) parameters (from model
r −i <2
lcdm+sz+lens as specified on LAMBDA website 37), mod mod
d >0.55
which are: a flat ΛCDM cosmology with Ω = 0.266, ⊥
M
Ωb =0.0449, h=0.71, and σ8 =0.801. ifiber2 <21.7
i <19.86+1.6×(d −0.8)
2. THEDATA cmod ⊥
c >1.6 (1)
2.1. Observations (cid:107)
The Sloan Digital Sky Survey (SDSS; York et al. where
(2000); Eisenstein et al. (2011)) mapped over a quarter
d ≡(r−i)−(g−r)/8≈r−i
⊥
37http://lambda.gsfc.nasa.gov/product/map/dr4/parameters.cfm c ≡0.7∗(g−r)+1.2∗(r−i−0.18) (2)
(cid:107)
4
The magnitudes denoted by ”cmod” are ”cmodel mag-
nitudes” (see White et al. (2011) for more discussions),
and the colors are defined with model magnitudes, ex-
cept for i , which is the magnitude in the 2(cid:48)(cid:48) spec-
fiber2
troscopic fiber (Stoughton et al. 2002; Abazajian et al.
2004). Note that we applied i <21.7, although the
fiber2
current BOSS target selection has moved the limit from
21.7 to 21.5. All magnitudes are extinction corrected
using maps of Schlegel et al. (1998).
In addition to constructing galaxy density maps, we
created several additional maps that we use to reject
regions heavily affected by sample systematics such as
Fig. 1.—Thefullimagingangularmaskinequatorialcoordinate
poor sky or stellar density, and to make sure our final
systemaftergeneratingauniquesetofallpolygonsthatcontains
power-spectra are free of systematics. These include (i) primary fields with good observing conditions. The colors repre-
a map of the full width at half-maximum (FWHM) of sentstheModifiedJulianDateofobservationofeachfield.
the point-spread function (PSF) in r band; (ii) a map
of stellar density (18.0 < r < 18.5 stars); (iii) a map of
sky brightness in i-band in nanomaggies38/arcsec2; (iv)
3 map of the color offsets in u−g, g−r and r−i from
Schlafly et al. (2010); (v) a map of Galactic extinction
simply rescaled from the extinction maps from Schlegel
et al. (1998).
2.3. Angular and Redshift Distributions
To interpret the clustering of any sample, one must
characterize the expected distribution of the sample as
if it is completely random. This involves understanding
boththeangularandradialselectionfunctioninaddition
totheexpectedgalaxydensity,whichischaracterizedby
Fig. 2.—Thepreliminaryimagingmaskafterapplyingprimary
its mean density.
selection cuts such as cuts on seeing and the bright star mask on
To characterize the angular window function, we gen- thefullimagingangularmask.
erate the complete angular mask of the survey following
the procedures described below. The observed sky is de- ily visible, and we can also see that the north and south
fined as a union of all fields. Determining the window Galacticcapsareobservedatsignificantlydifferentepoch
function requires identifying the fields that cover each ofthesurvey. Thisprovideshintastowhatpotentialob-
position on the sky and deciding which of those fields servational systematic effects would look like. To create
should be considered primary at that position. There is a more restrictive mask which is catered towards photo-
auniquesetofdisjointpolygonsontheskydefinedbyall metricredgalaxies, weproceedtoexcluderegionswhere
the field boundaries, which are calculated using MAN- E(B−V)>0.08 (Scranton et al. 2002; Ross et al. 2006;
GLE package 39(Hamilton 1993; Hamilton & Tegmark Padmanabhan et al. 2007; Ho et al. 2008), which is al-
2004; Swanson et al. 2008) and each field can be divided mostidentitaltoAr >0.2,whenseeinginthei-bandex-
intomultiplepolygons. Wenowmustdecidewhichfields ceeds 2.0(cid:48)(cid:48) in FWHM, and masking regions around stars
are primary for each polygon in the sky; the process is in the Tycho astrometric catalog (Høg et al. 2000). The
described in Aihara et al. (2011) in detail. Once we de- final angular selection function covers a solid angle of
termine which fields are primary for all the polygon in ∼11,000 square degrees, and is shown in Fig. 2.
the sky, we make a cut on the field observing conditions Applying the selection criteria in Sec 2.2 to the 14,555
(SCORE>=0.6;formoredetailsonSCORE,seeAihara deg2 ofphotometricSDSSimagingconsideredinthispa-
et al. (2011) or the SDSS-III webpage 40). We now have per yields a catalog of approximately 1,500,000 galax-
an unified MANGLE polygon file that includes all the ies. Applying the angular selection function as shown
fields that are imaged in the entire SDSS footprint, with in Fig. 2 to the Ross et al. (2011) photometric redshift
the correctly assigned primary fields with good observ- catalog yields a sample of 872,921 objects, 96% of which
ing conditions. We call this the "full imaging mask", as are believed to be galaxies (3% are stars, and 1% are
plotted in Figure 1. The color in Figure 1 represents the quasars, according to statistics gathered in the spectro-
date at which the imaging data was taken. The striped scopic sub-sample; Ross et al. (2011)). For every ob-
pattern perpendicular to the scanning direction is eas- ject, photometric redshifts and probabilities of being a
galaxies were determined using the ANNz Neural Net-
38http://data.sdss3.org/datamodel/glossary.html#nanomaggies work (Collister & Lahav 2004; Firth et al. 2003). The
39 http://spae.mit.edu/m˜olly/mangle calibration and accuracy of these data are discussed in
40 sdss3.org detail in Ross et al. (2011). In the range considered in
5
Label zmid Ngal bg
CMASS0 0.425 23517
CMASS1 0.475 154531 1.92±0.06
CMASS2 0.525 198132 1.98±0.05
CMASS3 0.575 190603 2.19±0.05
CMASS4 0.625 121181 2.19±0.05
CMASS5 0.675 54744
TABLE 1
Descriptions of the 6 ∆z=0.05 redshift slices; z is
mid
the midpoint of the redshift interval. Bias parameters
are deduced from marginalizing over all the other
cosmological parameters (and a free shot noise term)
from combining WMAP 7 + HST + DR8 angular
power-spectra likelihood using only 30<(cid:96)<150
multipoles. The first and last bins are dropped from
Fig. 3.— The redshift distribution of the photometric CMASS here on due to the small number of galaxies in those
sample when we match the objects with an unbiased sub sample bins.
fromSDSS-IIIBOSS.
ple is plotted in Fig. 3. We can see that although the
majority of the objects in one photometric-redshift bin
is in their corresponding true redshift bin, a significant
fraction of them fall into neighboring bins. The compar-
isons of these photometric redshifts to the spectroscopic
redshifts (obtained via SDSS III spectra) are plotted in
Fig.4,whilepropertiesofthedifferentslicesaresumma-
rized in Table 1. We see that the numbers of galaxies in
both the first and the last bins are significantly smaller
thantheothers,therefore,wedecidetodropthese2bins
fromouranalysis. Thisdecisionisalsofacilitatedbythe
fact that we wish to have a nearly independent sample
from the Reid et al. (2010); Percival et al. (2010) LRG
clusteringanalysis, thusallowingforsimplecombination
of their likelihoods in the cosmological parameter analy-
sis.
2.4. Sample Systematics
There are a number of potential systematic effects in
photometric samples that contaminate clustering: stel-
lar contamination and obsuration, seeing variations, sky
brightness variations, extinction and color offsets (such
Fig. 4.—Thephotometricvsspectroscopicredshiftdistribution as those described in Schlafly et al. (2010)). Ross et al.
of112,778ofSDSS-IIIBOSSCMASSgalaxies. (2011) had extensive discussions on these potential sys-
tematics; we will concentrate on the particular effects
this paper,the redshifts have calibrated errors ∼ 0.04 from various systematics on the angular power-spectra
at z ∼ 0.45 and ∼ 0.06 at z ∼ 0.65. We pixelize in the range of scales that affects our science analysis.
these galaxies as a weighted (with the probabilities of The above cuts remove only parts of the sky that are
being a galaxy) number overdensity, δ = δn/n¯, onto a significantlyaffectedbyextinctionandseeingvariations.
g
HEALPixpixelization (Gorskiet al.1999)of thesphere, With such a large sky coverage, an accurate determina-
with 12,582,912 pixels over the whole sphere (HEALPix tion of the angular power-spectra of the the large scale
resolution 10, nside=1024), each pixel covers a solid an- tracer is only possible through an thorough understand-
gle of 11.8 arcmin2. These pixelized maps are used di- ingofthesystematics. However,ifweonlyretainpartsof
rectly to compute the angular power-spectra using opti- the sky that have the minimum systematics effects; we
mal quadratic estimator. The optimal quadratic estima- must remove most of the coverage, as we have demon-
tor does not down-sample input pixelized maps, rather, strated in Ross et al. (2011). Therefore, we developed
it computes the covariance matrix directly from these a novel way of dealing with residual sample systematics
pixelized maps, and this will be discussed further in 3.4. which we will discuss in Sec. 5 in detail.
Thesampleisdividedinto6photometricredshiftslices
of thickness ∆z = 0.05 starting at z = 0.4 for CMASS 3. THEANGULARPOWERSPECTRUM
sample(CMASS0throughCMASS5,seeTable1forde- As was noted in the introduction, the angular power-
tails), and the underlying redshift distributions for each spectrum contains information of both the growth and
slice are calculated using BOSS spectroscopic redshift of the expansion of the Universe through two standard
the same sample. The redshift distribution of the sam- rulers of the Universe: the baryon acoustic oscillations
6
and the matter-radiation equality turn-over scale; thus constant shot noise term which is estimated by the opti-
theshapeofthepower-spectrum. Inthissection,wewill mal quadratic estimator and a is a constant term that is
describeboththetheoryandthecomputationofangular fitted as a freely floating parameter. This is a good ap-
power spectrum. proximation on large scales, but breaks down on smaller
scales; we defer a discussion of its regime of validity, as
3.1. From galaxy distributions to angular well as the nonlinear evolution of the power spectrum to
power-spectrum a later section of this paper 3.3.
The intrinsic angular galaxy fluctuations are given by: Throughout the paper, we adopt this linear redshift
independent (within our redshift slice) bias model with
(cid:90)
g(θˆ)= dzb(z)N(z)δ(χ(z)θˆ,z), (3) a constant shot noise term. The bias and the shot noise
termofgalaxysampleforthevariousredshiftslicesarefit
asextraparametersinCosmologicalMonteCarlo(COS-
where b(z) is an assumed scale-independent bias factor
MOMC; Lewis & Bridle (2002)) chains to ensure we do
relating the galaxy overdensity to the mass overdensity,
notbiasourcosmologicalmodelsviafixinganyparticular
i.e. δ = bδ, N(z) is the normalized selection function,
g pre-computed bias.
andχ(z)isthecomovingdistancetoredshiftz. Wefocus
on the auto power-spectrum of the galaxies: 3.2. Redshift-Space Distortions
2 (cid:90) The position of observed galaxies can be inferred from
Cgg((cid:96))= k2dkP(k)[g] (k)[g] (k) (4)
π (cid:96) (cid:96) their redshift, and hence the peculiar velocity along the
line-of-sight can in principle affect our angular power-
where P(k)=P(k,z =0) is the matter power spectrum spectrum. Sofarwehaveneglectedtheeffectofthepecu-
today as a function of the wave number k, and the func- liar velocity, i.e., the redshift-space distortion (RSD) ef-
tion [g](cid:96) is fectontheangularpowerspectrum. Inthe3-dimensional
(cid:90) redshift-space power spectrum measured with spectro-
[g] (k)= dzb (z)N(z)D(z)j (kχ(z)) (5) scopic surveys, the modeling of RSD is still challenging
(cid:96) i (cid:96)
due to the fact that the mapping process from real to
The Limber approximation, which is quite accu- redshift-space is nonlinear in terms of peculiar velocity.
rate when (cid:96) is not too small ((cid:96) > 10), can be For recent efforts, see for example Scoccimarro (2004);
∼
Taruya et al. (2010); Reid & White (2011); Seljak &
obtained from Eq. (4) by setting P(k) = P(k =
McDonald (2011). It is comparatively easy to model the
((cid:96)+1/2)/χ(z)) and using the asymptotic formula that
(2/π)(cid:82) k2dkj (kχ)j (kχ(cid:48))=(1/χ2)δ(χ−χ(cid:48)) (when (cid:96)(cid:29) RSD effect on the angular power spectrum, because the
(cid:96) (cid:96) RSD information along the line of sight is projected out
1). We find that the substitution k = ((cid:96) + 1/2)/χ(z)
in the angular clustering. Padmanabhan et al. (2007)
is a better approximation to the exact expressions than
formulated the RSD for the angular power spectrum at
k = (cid:96)/χ(z). Note that j (x) is the lth order spherical
l the linear level, and showed that the linear RSD effect
Bessel function. On large scales where the mass fluctu-
can be seen only at large scales ((cid:96) < 20). However we
ation δ (cid:28) 1, the perturbations grow according to linear
could imagine that, if we select thin redshift slices, the
theory δ(k,z) = δ(k,0)D(z)/D(0).
nonlinear RSD effect may not be projected out and be-
For auto-correlation, applying Limber approximation
comes non-negligible at small scales. Saito et al. (2012)
will change Eq. 4 to the following:
shows that such nonlinearities becomes important only
(cid:90) 1 in the case when σ <0.01 at (cid:96)>500 but this is not the
Cgg = dz b2(z)N2(z)P(k,z) (6) z
(cid:96) χ2(z) case here.
We here include the linear RSD effect following Pad-
For cross-correlation between two different large scale manabhan et al. (2007). To be complete, let us review
structuresamples(beitdifferentselectionfunctions,red- some of the important details from Padmanabhan et al.
shift distributions, different biases), we can write the (2007).
cross-correlation as follows:
(cid:90)
Cgg(cid:48) =(cid:90) dz 1 b(z)b(cid:48)(z)N(z)N(cid:48)(z)P(k,z) (7) 1+g(θˆ)= dχN(s)[1+δ(χθˆ,χ)], (9)
(cid:96) χ2(z)
wherewehavenowwrittenthenormalizedselectionfunc-
where g(cid:48) can have different biases, redshift dependence tionasafunctionofredshift-spacedistance,s=χ+v·θˆ
etc. with the peculiar velocity component, v. Assuming the
Wehavenotyetdistinguishedbetweenthegalaxyand peculiarvelocitiesaresmallcomparedwiththethickness
the matter angular power-spectrum yet. Throughout oftheredshiftslice,weTaylorexpandtheselectionfunc-
this paper, we simply assume tion to linear order,
C ((cid:96))=b2C (cid:96))+N +a , (8) dN
g g ( shot N(s)≈N(χ)+ (v·θˆ). (10)
dχ
where C ((cid:96)) and C (cid:96)) are the galaxy and matter angu-
g (
lar power spectra; b is the linear galaxy bias, N is a Substituting this expression into Eq. 9, we express sep-
g shot
7
arately the 2D galaxy density field in two terms, g = 3.3.1. Non-linear effects on the overall shape of the
g0 +gr, where g0 is the term discussed in the previous power-spectrum
section, while gr is the linear RSD correction. With the
Thereisanextensiveliteraturediscussinghowonecan
help of linear continuity equation, we have the Legendre
model the linearities of 3D power-spectrum over a large
coefficient as
range of scales (Sánchez et al. 2008; Carlson et al. 2009;
(cid:90) d3k Hamaus et al. 2010). This paper does not intend to ad-
δr((cid:96))=i(cid:96) Wr(k). (11) dresstheissueoffullymodelingthenon-linearitiesin3D
g (2π)3 (cid:96)
power-spectrum; we do, however, take a simple model
that happens to perform quite satisfactorily for the 2D
The component is given by
angular power-spectrum. We adopt the simple linear
β (cid:90) dN redshift-independentbiasingmodel(withshotnoisesub-
Wr(k)= dχ j(cid:48)(kχ), (12) tracted for every single angular power-spectra). There-
(cid:96) k dχ (cid:96)
fore, in addition to the cosmological parameters that are
where β is the growth parameter defined by β ≡ ofinterestforeachmodel,weincludethreeextraparam-
cdallnBDe/sdsellnfau/nbcgt,ioannwditjh(cid:96)(cid:48) riessptheectdteoriivtsatairvgeumofentht.eWspehcearin- e8t.ers for each redshift slice (b, Nshot and a) as shown in
then apply the fact that C ≡ (cid:104)g g∗(cid:105), and calculate the We test the sufficiency of this model in multiple ways.
redshift space distorted ang(cid:96)ular p(cid:96)ow(cid:96)er-spectra. We test this model by fitting only 2 < (cid:96) < 150 and 2 <
(cid:96) < 200 using simulated CMASS mocks (as is discussed
in Sec.3.5). We compute optimally quadratic estimated
3.3. Non-linearities
power-spectra of simulated data (a total of 160 realiza-
Non-linearities in the power-spectrum are caused by tions from 20 independent simulation boxes, 8 lines of
the non-linear evolution of components of the Universe, sight each), and then we compute 8 averaged (over 20
especiallythelatetimeevolutionofmatterandbaryons. independent simulations) power-spectra, and combined
To capture the full extent of the non-linearities, with it with a pseudo-WMAP7 likelihood (which has the co-
a lack of full-fledged non-linear evolution theory, one variances of WMAP7 likelihood, but with cosmologi-
will need to simulate the evolution of most if not all cal parameters centered on the input parameters of the
of the components of the Universe. Extensive research CMASS mocks. We find that when using above men-
and discussion have been carried out in multiple fronts tioned model for the averaged power-spectra, in combi-
(Sánchez et al. 2008, 2009), whether it is by perturba- nation with pseudo-WMAP7, we recover all input cos-
tion theory (Carlson et al. 2009), dark matter simula- mological parameters of the CMASS mocks for all 8 av-
tions (Hamaus et al. 2010; Heitmann et al. 2009), or eragedpower-spectratowithin1.5σ. Weconcludethata
fitting functions suggested by dark matter simulations spread over 1.5σ is reasonable. The bias parameters re-
(Smith et al. 2003). Historically, there are a few ways to covered are also similar to the input bias of the CMASS
deal with non-linearities in utilizing power-spectrum to mocks as described in White et al. (2011). We therefore
constrain cosmology, such as comparing the non-linear conclude that this model is accurate in recovering cos-
power-spectrum to the linear power-spectrum (usually mological parameters when used in the range of angular
for specific cosmological model), and keeping only scales scales as specified above.
that are believed to be linear (Tegmark et al. 2004; Pad- We further tests this model by comparing this model
manabhan et al. 2007); or utilizing the halo occupation with Hamaus et al. (2010), we found that our sim-
model to convert a galaxy power-spectrum into a halo ple method fits the non-linear power-spectrum derived
power-spectrum, which can be easily compared to halo from cosmological simulations quite well even up to k =
power-spectra from dark matter simulations(Reid et al. 0.2h/Mpc. In Figure 5, we plot the non-linear power-
2010); or using a variety of fitting functions developed spectrum from numerical simulations of halos (points
Carlson et al. (2009) to fit its observed galaxy power- witherrorbars),whilethesolidlinesarepower-spectrum
spectra (Blake et al. 2010). Our project both benefits of various halo mass bins calculated using our simple
and suffers from the fact that it is a photometric sur- model b2P (k)+ 1 , the model fits the non-linear
non−lin n¯
vey. Ononehand,itsBAOsignalissmearedaswedon’t power-spectrum quite well over a significant range in k
have accurate redshifts; on the other hand, the integra- evenwhenwehavenotyetaddedtheadditionalconstant
tion along lines of sight ameliorates the non-linearities term a. The dashed lines show the results without the
that would have been considerably stronger. Therefore, shotnoisetermforvarioushalomassbins. Ourmodelof
traditionally,angularpower-spectraanalysisusuallyonly non-linearpower-spectrumisbasedonHALOFIT(Smith
appliesasimplecutontheangularscalethatroughlycor- etal.2003),soinordertonotconfusethereader,wewill
responds to k =0.1kMpc−1 (Padmanabhan et al. 2007). call Pnon−lin(k) by Phalofit(k). The lower panel shows
In this paper, we take a small step forward in terms of theratiosbetweena≡P (k)−(b2P (k)+1/n)and
hh halofit
non-linearity treatment of the overall shape of angular P (k) are plotted as lines. The non-linear bias is fairly
hh
power-spectrum, and also adopt a similar treatment as wellfitbyoursimplemodelevenifwedonotincludethe
in Eisenstein et al. (2007); Blake et al. (2010) for the extra constant bias term. We decided to include the ex-
non-linear treatment on the BAO scales. traconstanttermatohelpremovetheresidualdifference
8
Fig. 5.— To justify our choice of scale for fitting our cosmo- Fig. 6.— We applied two different methods in calculating the
logical parameters, and the model we adopted, we show how well power-spectrum(includingtheBAO)withnon-lineareffectstaken
simple model such as b2P (k)+1/n+a can fit fairly well into account, and find that it makes very little difference in the
halofit
up to k = 0.2h/Mpc. Top panel shows the non-linear power- cosmologicalparameterconstraints.
spectrum of halos in a cosmological simulations (dots with er-
ror bars), the model being considered here b2Phalofit(k) + 1/n ting method with COSMOMC with Σnl set to 2hMpc−1
(solid line) and the dashed line shows what happens if we only higher and lower than its currently chosen value (7.527),
use b2(k)PNL(k) instead. Bottom panel shows a/Phh(k) where and find that when we fit for a ΛCDM model in combi-
a=Phalofit(k)+1/n,wecanseethattheratioisfairlyconsistent nation with WMAP7, there is less than 5% change for
with 0.0 for a large range of mass, and it starts to deviate from
any of the parameters.
0.0 starting at k = 0.1Mpc/h. Therefore, we find it prudent to
include an extra parameter a in our formalism, as we do include However, the addition of the nonlinear ratios is quite
some modes at k larger than k =0.1 Mpc/h. The different color important, not only because the power in small scales
lines correspond to different halo mass ranges. The largest halos
in the angular power spectrum at high multipoles is not
arethosewithhighestbias,whichalsogivesthelargestdeviations
expected to be accounted for the shot noise due to finite
fromthemodel.
number of galaxies, but also because the small shift in
between Phh(k) and b2Phalofit(k)+1/n. the BAO wiggles can slightly modify the best-fit shape
ofthepowerspectrumandhencereturnadifferentvalue
3.3.2. Non-linear effects on the BAO of Γ ≡ Ω h. We applied two different methods in cal-
m
Wetesttheeffectonourresultsofnon-linearevolution culating the power-spectrum (including the BAO) with
onthesmearingoftheBAOfeaturebyassumingthatthe non-linear effects taken into account, and find that it
non-linearmatterpowerspectrumfollowstheexpression makes essentially no difference (see Figure 6).
in Eisenstein et al. (2007):
3.4. Optimal Estimation of Angular Power Spectrum
P(k)=exp(cid:0)−k2Σ2 /2(cid:1)P (k)+
nl wiggle Thetheorybehindoptimalpowerspectrumestimation
(cid:0)1−exp(cid:0)−k2Σ2 /2(cid:1)(cid:1)P (k) (13) is now well established, so we limit ourselves to details
nl no−wiggle
specifictothisdiscussion,andreferthereadertothenu-
where Σnl = 7.527h−1Mpc, Pwiggle(k) is the linear merous references on the subject (Hamilton 1997; Seljak
theory power-spectrum (which includes the BAO) and 1998, and references therein). We also refer the reader
Pno−wiggle(k)isasmoothpowerspectrum,withthesame to the Appendix A for more specific details that relate
shapeasPwiggle(k)butwithoutanybaryonicoscillations; to our paper directly.
which is computed using the approximation described We start by parametrizing the power spectrum with
in Eisenstein & Hu (1998). Both the wiggle and the twenty step functions in l, C˜i,
no-wiggle part have been computed in linear theory; we l
then added to both of them the corresponding nonlinear C =(cid:88)p C˜i , (14)
ratios as a function of the scale. This approach signifi- (cid:96) i (cid:96)
i
cantly enhances the power in small scales. We find that
the results are not very sensitive to the exact value of wherethepiaretheparametersthatdeterminethepower
Σ provided that it is in the range of 5.527 to 9.527 spectrum. We form quadratic combinations of the data,
nl
h−1Mpc(Eisensteinetal.2007). Inprinciple,Σ iscos-
nl 1
mology dependent, and thus can change our cosmologi- q = xTC C−1C x , (15)
i 2 i i
cal constraint if it is kept as a free parameter. We have
therefore examined our constraints on cosmological pa- wherexisavectorofpixelizedgalaxyoverdensities,Cis
rametersusingdifferentΣ . Wetestthisissuebyfitting the covariance matrix of the data, and C is the deriva-
nl i
the full set of cosmological parameters using MCMC fit- tive of the covariance matrix with respect to p . The
i
9
covariance matrix requires a prior power spectrum to
account for cosmic variance; we estimate the prior by
computing an estimate of the power spectrum with a
flat prior and then iterating once. We also construct the
Fisher matrix,
F = 1tr(cid:2)C C−1C C−1(cid:3) . (16)
ij 2 i j
The power spectrum can then be estimated, pˆ = F−1q,
with covariance matrix F−1.
WealsoreferthereadertoAppendixAfordetailsmore
specific to our project.
3.5. Tests with simulations
To test whether the errors estimated by the quadratic
estimator employed here are accurate or not and to test
the results of our pipeline, we must compute the errors
obtained via a series of simulations.
One way to do this is to generate Gaussian random
field using the prior power spectra for each redshift slice
to simulate over the entire sphere. We can Poisson dis-
tribute galaxies with probability (1+δ)/2 over the sur-
vey region, trimmed with the angular selection function.
Padmanabhan et al. (2007) has tested this pipeline with
the Gaussian random fields simulations, thus what we
need to test here is whether the errors estimated by the
quadraticestimatorareappropriate,consideringthatthe
power-spectrum measurement is only minimum variance
measurement when the field is Gaussian, which is not
the case here. Given the non-gaussianity of the field, we
needtodeterminehowclosewearetominimumvariance
measurement.
As we would like to simulate our galaxy sample as
closely as possible, we employed CMASS mock catalogs
from White et al. (2011) to test the accuracy of the op-
timal quadratic estimator. White et al. (2011) has pro-
ducedaseriesofmockcatalogsthatusethebest-fitHOD
models from White et al. (2011), and populate a series
of N-body simulations (White et al. 2011). The major-
ity of the galaxies are central galaxies living in halos of
mass1013h−1M . Wegenerate8linesofsightfromeach
(cid:12)
cornerofeachofthe20independentCMASSsimulations
from White et al. (2011). These mock catalogs are then
processed the same manner as the real data through the
quadraticestimatorcode,andanalyzedinthesameman-
nerastherealdataset. Themockangularpower-spectra
are thus optimally estimated angular power-spectra.
We plotted the distribution of the power-spectrum
fromeachsimulationthatareestimatedbythequadratic Fig. 7.— (top)The estimated (from Optimal quadratic estima-
estimator code, and compare these results to the aver- tor)powerspectrumfrom160simulatedrealizations(redcrosses)
out of 20 independent dark matter only simulations (White et al.
aged error-bar of the simulation (see Figure 7). When
2011). The green points show the averaged recovered power-
comparing the expected error to the distribution of esti- spectrumfromeachofthesimulations,whilethebluepointsshow
matedpower-spectrumfromeachsimulationandtheav- theaveragedmeasurederrorasestimatedfromoptimalquadratic
eragedmeasurederrorfromeachsimulation,weconclude estimator. Weconcludethattheaveragedmeasurederrorfromthe
optimalquadraticestimatorisagoodmeasureoftheexpecteder-
that the averaged measured error is a good measure of
ror. (middle)Theestimatederror(redcrosses)isbaseduponthe
the expected error. We have plotted the estimated error varianceoftheestimatedpower-spectrumfromeachsimulationat
(redcrossesofthemiddlepanelofFigure 7)byexamin- eachell-mode. Wehavealsoplottedtheaveragedmeasurederror
ing the variance of the estimated power-spectrum from (greenpoints),anditisabithigherthantheestimatederrorfrom
the variance of the simulations (bottom panel). Nevertheless, we
each simulation at each (cid:96)-mode. We have also plotted
showthatthequadraticestimatorcodecanestimatetheerrorsof
the power-spectrum in the scale of interest here with reasonably
highaccuracy.
10
the averaged measured error (green points), and it is a tions(whichcannotcomefromgalaxyauto-correlations),
bit higher than the estimated error from the variance of therefore, we know that there is significant systematics
the simulations (bottom panel). This is probably due to withinCMASS1. Thebottompanelshowsthatthehigh
the fact that since there are only 20 simulation boxes, redshift slice CMASS 4 also has substantial effects from
with 8 lines-of-sights overlapping slightly in within each systematics.
box. Therefore, the variance of simulated C is probably Finally, to estimate whether it is worth including the
l
slightlysmallerthanitshouldbeatallscales,duetothe cross-power of various redshift slices into the cosmologi-
correlations between lines of sight. Regardless, we show cal analysis, we performed a simple Fisher analysis. We
that the quadratic estimator code can estimate the er- calculatedFishermatricesusingangularspectrafromthe
rors of the power-spectrum in the scale of interest here four redshift bins (CMASS 1-4), with the redshift distri-
with reasonably high accuracy. It is important to note butionsgiveninFigure3. AstandardΛCDMcosmology
that at all scales of interest (to the current paper), the is employed to calculate the fiducial spectra. We used
estimated error from the quadratic estimator codeis not the Limber approximation (where the input power spec-
under-estimated. trum was given by CAMB 41 linear power-spectrum and
HALOFIT) and ignored redshift space distortions. We
3.6. The Optimally Estimated Angular Power Spectrum employ the standard Gaussian expression for the covari-
ance matrix of the spectra. The shot noise term was
The angular power-spectra estimated using the
calculated assuming N = 1/n¯ (with n¯ being the num-
methodology described in Sec 3.4 are displayed in Fig- l
ber of galaxies per steradian of the individual bin). Fi-
ure8. Inparticular,weplotseparatelythenorth(Galac-
nally, to construct the Fisher matrix, we used the range
tic), south and full angular power-spectra of these 4 red-
l=30−300. Theparameterspaceisgivenby: Ω ,Ω ,Ω ,
shift bins (CMASS 1-4, from z =0.45−0.65). We plot- b c ν
Ω ,σ ,n ,b ,b ,b andb (b referstobiasesofgalaxy
tedthenorthandsouthseparatelytoinvestigatepossible Λ 8 s 1 2 3 4 N
sample at redshift slice N). The Fisher matrix is then
systematic differences due to the long separation of ob-
added to WMAP7 Fisher matrix and invert to find the
servation time between north and south galactic caps.
covariance matrix for the parameters. We then consider
For the scales of interest (30 < (cid:96) < 150), the north and
twocases: (1)usingonlytheauto-spectraasobservables
southarenotdifferenttopromptseparateanalyses. Nev-
and (2) using both auto- and cross-spectra as observ-
ertheless,thisdoesnotprecludepossibilityofsystematic
ables. The errors on allparameters improve by less than
differences at the largest scales (at low multipole) in the
5%ingoingfrom(1)to(2). Wealsofoundthatignoring
angular power-spectrum. This is only possible, since the
covariancesbetweendifferentauto-spectra(wedoinclude
estimated power in each (cid:96)-bin is not correlated, there-
the covariance between auto power-spectra in the anal-
fore a systematic difference in one (cid:96)-bin does not affect
ysis) makes less than 5% difference. This suggests that
another.
whenweincludethesecovariancesintheMCMC,theer-
To test the similarity of north and south region on
rors will not change significantly. We therefore adopt a
scales of interest ( 30<(cid:96)<150), we find all best fit cos-
conservative approach where we don’t include the cross-
mology parameters (with combined with WMAP7, via
power as extra signal, but we include the bin-to-bin co-
MCMC chain using COSMOMC) found by north and
variancethatcan,inprinciple,bedouble-counteddueto
south alone respectively are consistent with each other.
the overlap of redshift slices.
It is interesting to note that the south has smaller area
thanthenorth,andthustherearelessinformationperl-
4. POTENTIALSAMPLESYSTEMATICS
bin,thustheerror-barsinthesouthissignificantlylarger
than the north. It will also be discussed later in Sec 4 Without accurately addressing known potential sys-
as the systematic treatment presented in this paper will tematics on the observed number density of objects in
in principle correct systematic variations even when the our sample, we cannot claim to understand its expected
full survey is analyzed in one piece. We can also see angular power-spectra, nor can we extract cosmological
the evolution of the angular power-spectra over different information from it. The treatment of systematics is es-
redshift slices, as it is expected. pecially crucial for the overall shape of power-spectrum,
AsshowninFigure3,weneedtoinvestigatethepoten- since the shape does not deviate much from power-laws,
tial effects of overlapping redshift distributions. We cal- and has no specific features such as those in BAO. The
culate the cross-power of various redshift combinations, oscillatory nature of the BAO signal helps it from be-
and they are shown in Figure 9. Cross-power between ing contaminated by any systematic signal that doesn’t
different redshift bins not only add information in terms have oscillatory features. Moreover, most BAO detec-
of cosmology, but also from the perspective of systemat- tion methods attempt to minimize any influence from
ics. the shape directly (Eisenstein et al. 2007), thus further
When we examine cross-power across various redshift shieldingtheBAOtechniquefromanysystematiceffects.
bins, any difference between the measured power and We will propose a novel method of systematic correc-
theexpectedpower(fromgalaxyauto-correlationsinthe tions in Sec 5 which helps mitigate the effects in power-
same redshift range) can be used as a measure of the spectrum caused by any systematics.
effects of systematics. In the top panel, there is signifi-
cantextrapoweratlargescale,andalsonegativecorrela- 41 http://camb.info/