Arbitrarily Degenerate Helium White Dwarfs as Donors in AM CVn Binaries

0.49 MB·

by  Christopher J. Deloye

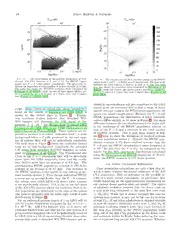
Draftversion February2,2008
PreprinttypesetusingLATEXstyleemulateapjv.7/15/03
ARBITRARILY DEGENERATE HELIUM WHITE DWARFS AS DONORS IN AM CVN BINARIES
Christopher J. Deloye
DepartmentofPhysics,BroidaHall,UniversityofCalifornia,SantaBarbara,CA93106 1
Lars Bildsten
KavliInstitute forTheoreticalPhysicsandDepartmentofPhysics,KohnHall,UniversityofCalifornia,SantaBarbara,CA93106
and
Gijs Nelemans
DepartmentofAstrophysics,RadboudUniversityNijmegen,P.O.Box1910,NL-6500GLNijmegen,TheNetherlands
5 Draft versionFebruary 2, 2008
0
0 ABSTRACT
2
We apply the Deloye & Bildsten (2003) isentropic models for donors in ultracompactlow-massX-ray

n binaries to the AM CVn population of ultracompact, interacting binaries. The mass-radius relations
a of these systems’ donors in the mass range of interest (M2 < 0.1M⊙) are not single-valued, but
J parameterized by the donor’s specific entropy. This produces a range in the relationships between

6 system observables, such as orbital period, P , and mass transfer rate, M˙ . For a reasonable range
orb
2 in donor specific entropy, M˙ can range over several orders of magnitude at fixed P . We determine
orb
the unique relation between M˙ and M in the AM CVn systems with known donor to accretor mass
1 2
v ratios, q = M2/M1. We use structural arguments, as well as each system’s photometric behavior, to
7 place limits on M˙ and M in each. Most systems allow a factor of about 3 variation in M˙ , although
2
7 V803Cen, if the currentestimates of its q areaccurate,is an exceptionandmust haveM2 ≈0.02M⊙
5 and M˙ ≈10−10M⊙ yr−1. Our donor models also constrain each donor’s core temperature, Tc, range
1
and correlate T with M . We examine how variations in donor specific entropy across the white
0 c 2
dwarf family (Nelemans et al. 2001b) of AM CVn systems affects this population’s current galactic
5
distribution. Allowing for donors that are not fully degenerate produces a shift in systems towards
0
/ longer Porb and higher M˙ increasing the parameter space in which these systems can be found. This
h shiftincreasesthefractionofsystemswhoseP islongenoughthattheirgravitywave(GW)signalis
orb
p
obscuredbythebackgroundofdetacheddoublewhitedwarfbinariesthatdominatetheGWspectrum
-
o below a frequency ≈2 mHz.
r Subject headings: binaries: close—gravitationalwaves—stars: AM CVn
t
s
a
: 1. INTRODUCTION servedspectrallinebroadeningrequiresacompactaccre-
v
tor(Nather et al.1981;Patterson et al.1993;Ruiz et al.
i The AM CVn class of variable stars are He-rich ob-
X 2001; Groot et al. 2001) while their weak X-ray emis-
jects which show a striking absence of H and photo-
sion indicates the accretor is a WD (Nather et al. 1981;
r metric and spectroscopic variations with periods of ≈
a Ruiz et al. 2001; Ulla 1995).
300-4000 s (see Warner 1995, for an overview). These
Because AM CVn systems are undergoing mass trans-
periods appear to be orbital and the commonly held
fer, we can constrain the donor’s structure from the or-
modelforthesesystemsisthatofamass-transferringbi-
bital period, P . For stable mass transfer, the donor’s
narywitha low-massHe white dwarf(WD) donoranda orb
radius,R ,mustequalitsRochelobe’sradius,R ,which
C/OorHeWDaccretor(Paczyn´ski1967;Faulkner et al. 2 L
can be approximated as
1972). This model is supported by several lines of ev-
idence: the spectra are dominated by double peaked M 1/3
lines (e.g., Marsh et al. 1995; Groot et al. 2001), imply- RL ≈0.46a 2 , (1)
(cid:18)M +M (cid:19)
ingthepresenceofanaccretiondisk(Nather et al.1981; 1 2
Nasser et al. 2001), rapid photometric flickering is ob- when q ≡M2/M1 <0.8 (Paczyn´ski 1967). Here M1 and
served, suggesting ongoing mass transfer (e.g. Warner M2 arethemassesoftheaccretoranddonorrespectively
1972;Warner & Robinson1972),and,inseveralsystems, and a is the orbital separation (throughout, we assume
the spectral line profiles vary with a stable, regular pe- thattheorbitiscircular). CombiningRL =R2 withKe-
riod coincident with one of the primary photometric pe- pler’sthirdlawleadstotheperiod-meandensityrelation,
riods, indicating this is the system’s P (Nather et al.
orb 3/2 1/2
1981; Nelemans et al. 2001a). These systems’ large ob- P ≃101s R2 0.1M⊙ . (2)
orb
(cid:18)0.01R⊙(cid:19) (cid:18) M2 (cid:19)
Electronicaddress: [email protected]
Electronicaddress: [email protected] In analyzing and modeling AM CVn systems, it is cus-
Electronicaddress: [email protected] tomary to specify a mass-radius, M-R, relation for the
1 currentlyatDepartmentofPhysics&Astronomy,Northwest-
donor producing a one-to-one relation between M and
ernUniversity,2131TechDrive,Evanston,IL60208 2
P .
orb
2 Deloye, Bildsten, & Nelemans
TwosuchM-Rrelationshavebeenutilizedextensively, In§2,wesummarizethedetailsofourmodelsandcom-
each motivated by a different AM CVn formation chan- pare their continuous M-R relations to the discrete set
nel. In both of these channels, severalcommon envelope of M-R relations above. We highlight how a range in
(CE)episodes(see,e.g.,Paczynski1976;Yungelson et al. the donor’s physical parameters translates into a range
1993) are involved in producing a close binary pair con- in observables,focusing on the relation between the sec-
sisting of a degenerate WD accretor and a low-mass ular mass transfer rate, M˙ , and P . We apply our
orb
He core remnant. The latter may eventually becomes models to the known AM CVn binaries in §3. For sys-
the donor when and if gravity wave angular momentum tems where q = M /M is known or inferred, there is
2 1
losses bring the pair into contact. In the first channel, a single-valued relation between M˙ and M . Making
2
which we will refer to as the WD-channel, this He ob-
reasonable assumptions about the nature of the donor
jectneverignitedafter the endofthe CEphase,andthe and accretor, we place limits on M˙ and M . Our mod-
donormakescontactasa(possiblysemi-)degenerateHe 2
els provide a connection between these constraints and
WD. In this case,the donor is typically modeled using a
limits on the donor’s specific entropy, the first such con-
T =0M-RrelationsuchasthatofZapolsky & Salpeter
straints on the AM CVn donors. With the current ob-
(1969) (e.g., Nelemans et al. 2001b). In the other chan-
servations, this does not yet provide a strong constraint
nel, which we refer to as the He-star channel, the He
ondonorproperties(exceptpossiblyforthecaseofV803
object is able to ignite He and makes contact as a He-
Cen which must have T < 106 K given its assumed q).
burning star (Savonije et al. 1986; Tutukov & Fedorova c
With stronger observational limits, we may be able to
1989; Ergma & Fedorova 1990; Nelemans et al. 2001b).
constrain the donor’s prior evolution and possibly pro-
Forthischannel,Nelemans et al.(2001b)usedafittothe
vide a means of determining individual system’s forma-
evolution track of model 1.1 from Tutukov & Fedorova
tion channel. In §4, we use our models to explore how a
(1989) to obtain a donor M-R relation, while Warner
rangeindonorspecificentropyatcontactinWD-channel
(1995) has also quoted a M-R fit to the Savonije et al.
AM CVn systems alters the M˙ , P distribution from
(1986)evolutionarycalculation. Inadditiontothesetwo orb
that calculated assuming a T = 0 M-R relation. A siz-
channels,Podsiadlowskiet al.(2002,2003)haverecently
able fraction of systems in this population make con-
proposed a scenario involving stable mass transfer from
tact within several 100 Myr or so of the end of the last
aH-depletedmainsequencestarthatcouldalsoproduce
CEphase(Tutukov & Yungelson1996),notallowingthe
AMCVnsystems. ThepotentialcontributiontotheAM
donors to cool much before mass transfer begins. These
CVn population from this channel has not be systemat-
highspecificentropydonorsfollowtracksthatdifferfrom
ically explored nor have M-R relations for the donors
the T =0 evolutiontrack. The consequence is apopula-
produced in this channel been reported.
tion that occupies a larger region of M˙ -P parameter
These sets of M-R relations have been used exten- orb
space. In general, higher entropy donors follow tracks
sively to approximate the properties of known sys-
shifted towards longer P relative to fully degenerate
tems (e.g., Warner 1995; Provencalet al. 1997; Marsh orb
donors. We also discuss how this calculation impacts
1999; Nasser et al. 2001; El-Khoury & Wickramasinghe
the gravity wave, GW, signal produced by this popula-
2000; Nelemans et al. 2001a; Wood et al. 2002) and in
tion. In particular, by the shifting of systems with hot-
AM CVn population synthesis studies (Nelemans et al.
ter donors to longer P , the number of AM CVn sys-
2001b; Farmer & Phinney 2003). However, the use of orb
tems, relativeto a populationwith only fully degenerate
discrete,single-valuedM-Rrelationslimits what we can
donors, that will be undetectable behind the detached
learnaboutthesesystems. Forexample,theydonotpro-
WD-WD binary GW background increases. Finally, in
vide a means of inferring internal donor properties from
§5wesummarizeourresultsanddiscussfuturedirections
observations. Nor do they allow us to model the effects
for study.
of the expected differences between systems formed in
a given channel. For example, in the WD-channel there
shouldbevariationsinthedonor’sentropyatinitialcon- 2. HOTLOW-MASSHELIUMDONORS:IMPLICATIONS
tact (Tutukov & Yungelson1996; Bildsten 2002). In the FORINTERACTINGBINARIES
He-star channel, the amount of He burned to C impacts Details concerning the calculation of our low-mass
the system’s minimum Porb and the donor’s subsequent He models can be found in Deloye & Bildsten (2003).
evolution (Ergma & Fedorova 1990). A discrete set of Briefly, we integrate hydrostatic balance using a mod-
M-R relations does not allow us to model the impact ernequationofstate (EOS)(Chabrier & Potekhin1998;
of these differences on the AM CVn population nor to Potekhin & Chabrier 2000) that includes realistic treat-
interpretpotentialobservationalsignsofsuchvariations. ment of Coulomb contributions, which are important at
Progress on these fronts has been hampered by a lack thelowdensitiesoftheselow-massobjects. Knowingthe
of models in the mass range (M2 < 0.1M⊙) applicable internalthermalprofileofanobjectisimpossiblewithout
to the AM CVn donors. Our recent calculation of mod- followingagivenevolutionaryscenario,soweassumethe
els for low-mass donors in ultracompact low-mass X-ray limiting case of an adiabatic internal profile; see DB03
binaries (Deloye & Bildsten 2003, hereafter DB03) now for further justification. We calculate models for 2 ≤
provides a set of models continuously parameterized by log(T /K) ≤ 7.9 and 2.0−2.3 ≤ log(ρ /gcm−3) ≤ 6.6
c c
thedonor’sspecificentropyinthisregime. Incontrastto (the lower limit depending on T ) to produce a set of
c
theaboveM-Rrelations,ourmodelset’sM-Rrelationis models parameterized by specific entropy.
not single-valued, therefore allowing us to make connec- WeshowinFigure1theM-RrelationsforourHemod-
tionsbetweenthe macroscopicandinternalpropertiesof els by the solid lines. Each line shows a sequence with
the donor. In this paper we apply the DB03 models to the same T and terminates with models that fill their
c
the AM CVn binaries. R at P ≈ 170 min. The coldest isotherm (T = 104
L orb c
Arbitrarily Degenerate Donors in AM CVn Systems 3
Fig. 1.—AcomparisonbetweentheHeWDmodelsofDB03and Fig. 2.— The relation between M˙ and Porb for fixed M1 =
the M-Rrelations currently used inthe AMCVnliterature. The 0.6M⊙ as produced by our He WD models. The solid lines show
solid lines show a set of isotherms for the DB03 He WD models this relationat constant Tc =104,106,5×106, and 107 K (from
with log(Tc/K) between 4.0 and 7.5 at intervals of ∆log(Tc/K) bottom to top). The symbols indicate where along each isotherm
=0.5. ThelowerdashedlineshowstheT =0Zapolsky&Salpeter M2 = 0.01M⊙ (triangles), 0.02M⊙ (squares), and 0.05M⊙ (pen-
(1969) He WD relation. The upper dashed line shows the M-R tagons). Alongseveralhotterisotherms,thesamemassisindicated
relationsfortheHe-starchannel usedbyNelemansetal.(2001b). attwopoints,asituationresultingfromtheexistence ofbothup-
The dotted lines show the RL filling solutions at the Porb of the per and lower branch models at these Tc. In these cases, for the
indicatedsystems(seeTable1forthesesystem’sparameter). shorterPorbpoint,thedonorisonthelowerM-Rbranch,whilefor
thelongerPorbpoint,thedonorisontheupperM-Rbranch. The
Tsugawa&Osaki(1997)Hediskstabilitycriteria(with q=0.05)
are shown by the dashed lines. At longer Porb, allowing for hot
donorsproduces aseveralordersofmagnituderangeinM˙.
K) is equivalent to the T = 0 M-R relation. The differ-
ence in this curve and the Zapolsky & Salpeter (1969)
relation as fit by Nelemans et al. (2001b) (the lower
P ,the minimumM adonorcanhaveandsatisfythis
dashed line) is due to the more simplified treatment of orb 2
constraint is set by the intersection of each dotted line
CoulombphysicsintheZapolsky & Salpeter(1969)EOS
with the T = 0 M-R relation. For M greater than this
as compared to that of Chabrier & Potekhin (1998) and 2
minimum, there is a continuous set of R filling solu-
Potekhin & Chabrier (2000). The turn-over in the M-R L
tions parameterized by the donor’s entropy. Thus, at
relations seen at low T is due to Coulomb interactions
c fixed P , the donor’s specific entropy determines M .
becoming the dominant source of binding in the WD. orb 2
OnthelowerbranchoftheM-Rrelations,hotterdonors
As T increases, thermal contributions to the EOS at
c must be more massive as seen along the dotted lines in
low density eventually dominate Coulomb contributions
Figure 1.
and the M-R relation no longer turns over (for He ob-
ThefactthatM andR cantakeonarangeofvalues
jects, this occurs for T ≈ 105 K, DB03). For higher T , 2 2
c c produces a range in binary parameters that is related to
there is a minimum mass below which equilibrium mod-
the donor’s specific entropy. To illustrate this, consider
elsdonotexist(Cox & Guili1968;Cox & Salpeter1964;
M˙ , which, assuming conservative mass transfer, is given
Hansen & Spangenberg 1971; Rappaport & Joss 1984)
by
that is related to the transition between thermal pres-
M˙ J˙ 1
sure and degeneracy pressure dominating the object’s
=2 . (3)
structure (Deloye & Bildsten 2003). Correspondingly, M2 (cid:12)J(cid:12)n+5/3−2q
for each isotherm, there are 2 branches to the M-R re- (cid:12) (cid:12)
Here J is the orbital(cid:12) a(cid:12)ngular momentum, J˙ < 0
lation: an upper branch where the object is thermally
the angular momentum loss rate from GW emission
supported and a lower branch where degenerate elec-
(Landau & Lifshitz 1962) and
trons provide the dominant pressure support. For a
wfixheidle Mon2,thoenutphpeerlowbrearnbchra,nRch,dRec2reianscerseawseitshwinitchreTasc-, n≡ ∂ lnR2 . (4)
2 ∂lnM
ing T (a fact related to the negative heat capacity of 2
c
thermally supported stars). For comparison, the upper Throughout this paper we assume that the donor re-
dashed line shows the Nelemans et al. (2001b) fit to the spondsadiabaticallysothatn is calculatedalongawell-
He-star M-R track of Tutukov & Fedorova (1989) used defined adiabat. This is equivalent to assuming that no
in the Nelemans et al. (2001b) population synthesis cal- specificentropyisgeneratedorlostinthedonorandthat
culation and elsewhere. M˙ is high enough that the orbital evolution timescale is
The dotted lines in Figure 1 show M-R relations re- shorter than the donor’s cooling time. This latter as-
quired for the donor to fill it Roche lobe (equation 2) at sumption seems well justified for ultracompact binaries
the P for the indicated AM CVn systems. At fixed (Bildsten2002),butsee§4forafurtherdiscussionofthe
orb
4 Deloye, Bildsten, & Nelemans
donor in this case follows an adiabat set by its specific
entropyatcontact. Thecoretemperaturedecreaseswith
M as the donor expands along the adiabat. We show
2
a few of the resulting M˙ -P evolution tracks in Figure
orb
3 calculated from the initial conditions M1,i = 0.6M⊙
M2,i = 0.2M⊙. The solid lines show tracks for our He
models starting on the lower, degenerate, branch of the
M-Rrelations,eachlinecorrespondingtoadifferentini-
tial T (between 104 and 6 × 107 K). The dot-dashed
c
show hot models initially on the upper branch. The
dashed lines show the evolution along the He-star (up-
per dashed line) and T =0 (lower dashed line) tracks of
Nelemans et al. (2001b). Donors from the WD-channel
are much less likely to make contact while on the upper
branch (due to their rapid cooling while hot). Objects
thatdo makecontactwhile onthe upper branchwillfol-
lowtrackssimilartothedot-dashedlinesatmuchhigher
M˙ than the those with T = 0 donors (shown by the
lowest solid line Figure 3). The distribution of M˙ at a
Fig. 3.— The relation between M˙ and Porb along evolution- specific Porb depends on the distribution of the donors’
ary tracks. Each line shows evolution from an initial configu- specific entropy at contact (assuming donors evolve adi-
ration of M2,i = 0.2M⊙ and M1,i = 0.6M⊙. The solid lines abatically). We discuss in §4 the properties of this dis-
show the adiabatic evolution of our He WD models initially with tribution in the context of the WD-channel population
Tc =104,107,3×107, and6×107 K (lefttoright)onthe lower synthesis model of Nelemans et al. (2001b).
branchoftheM-Rrelations. Thedot-dashedlinesshowthesame
for initial Tc = 6×107 and 5×107 K (again, left to right) on The AM CVns produced through the He-star channel
the upper branch. The dashed lines show the evolution using the willhave,onaverage,donorswithhigherspecificentropy
Nelemansetal.(2001b)fitsfortheT =0(lower)andHe-star(up-
than those from the WD-channel, thus populating a re-
per)M-Rrelations.
gion in Figure 3 above the T = 0 track. The track pro-
ducedbytheNelemans et al.(2001b)fittoaHe-starevo-
lution (the upper dashed line in Figure 3) provides one
such example. The difference in the slope of this track
validity of this assumption. With equations (2) and (3),
andtheDB03adiabatsmaybeduetoseveralcauses—the
we relate M˙ to P based on M , R , n, and assuming
orb 2 2 donorcoolingoverthecourseoftheTutukov & Fedorova
some value for M .
1 (1989)calculationisonepossibility,differencesinthein-
Firstconsiderthisrelationassumingthereisnorestric-
ternal structure of the models another—and indicates
tiononT (otherthanitislowenoughsothatHeburning
c that the approximations inherent in our models and in
cannot occur) at any Porb. In this case, M˙ can vary by calculating their evolution are only a first step towards
as much a factor of 100 or more at fixed Porb. This is a more realistic understanding of compact binary evolu-
illustrated in Figure 2 by the solid lines, which show the tion. We willdiscuss somefuture directionsforimprove-
M˙ -Porb relation along lines of constant donor Tc assum- ments to our calculations below.
ing a fixed M1 = 0.6M⊙ (M˙ varies a small amount for
M1 = 0.4−1.4M⊙). It should be noted that these lines 3. APPLICATIONTOTHEKNOWNAMCVNSYSTEMS
do notrepresentanevolutionarysequence, sincen along
We now apply our models to the AM CVn systems
an adiabat is used to calculate M˙ . Instead, they show
and determine the constraints that observations place
the parameters needed for a system to have some M˙ at on the binary and the donor. Each binary has a range
agivenPorb. Thedashedlinesshowtheupperandlower in M2 over which the donor can fill its Roche Lobe,
thermal stability criteria for a He disk as determined by leading to a range of possible binary parameter. For
Tsugawa & Osaki(1997). Abovetheupperline,thedisk most AM CVn systems, q = M /M has either been
2 1
is in a high-luminosity stable state; below the lowerline, spectroscopically measured (Nather et al. 1981; Marsh
the disk is in a low-luminosity stable state. For systems 1999) or can be inferred from P and the so-called
orb
located between these two lines, the disk is expected to superhump period observed in many of the AM CVn
exhibit periodic outbursts (see the discussion in §3). A systems (Whitehurst 1988; Hirose & Osaki 1990, 1993;
population of AM CVn binaries with variable evolution Ichikawa et al. 1993; Solheim et al. 1998; Skillman et al.
histories should be expected to have a range in M˙ at 1999;Provencalet al.1997;Pattersonet al.1997,2002).
fixed P , with M˙ providing a diagnostic of M and T In all cases q <0.1 (see, e.g., Woudt & Warner 2003, as
orb 2 c
in individual systems. Additionally, the rate at which a well as Table 1) . We use these q to obtain a unique
given AM CVn systems evolves in M2 and in Porb also relation between M˙ and M2 for each AM CVn system.
varies with the donor’s specific entropy (DB03). Theserelations,calculatedusingequation(3),areshown
The plausible range in Tc for a given Porb depends in Figure 4 by the solid lines.
on the formation channel and past evolution so that the The minimum value of M for each system is set by
2
range in M˙ at longer P will depend on the properties the intersection of the DB03 T = 0 M-R relation with
orb
of the progenitor population. We show this by consid- the Roche-lobe filling solutionto equation (2) at the ap-
ering adiabatic evolution from the minimum P . The propriate P (see Figure 1). The upper limit on M is
orb orb 2
Arbitrarily Degenerate Donors in AM CVn Systems 5
1998; Wood et al. 2002; O’Donoghue & Kilkenny 1989;
Pattersonet al. 2000; Abbott et al. 1992), while the
long period systems, GP Com and CE 315, are con-
sistently faint and again do not exhibit large ampli-
tude brightening (Richer et al. 1973; Ruiz et al. 2001;
Woudt & Warner 2001). This behavior is believed to be
explainedwithathermal-tidalHeaccretiondiskinstabil-
ity model (Smak 1983; Tsugawa & Osaki 1997) that re-
latesM˙ to thesedifferentobservedphotometricregimes.
TakingtheTsugawa & Osaki(1997)results,weusetheir
stability criteria to place limits on the allowed M˙ in the
AM CVn systems based on the photometric behavior of
each. In some cases, disk stability gives stronger con-
straints than those above and we show these additional
limits in Figure 4 as upper and lower limits on M˙ .
Fromour He WD models, we canalsodetermine T as
c
afunctionofM ineachsystem. Weindicatethemodels
2
withT =105,106,and107 Kbyopencirclesalongeach
c
system’s M˙ -M relation in Figure 4. We summarize the
2
Fig. 4.—For thesystems listedinTable1,the solidlinesshow limits placed on these systems from donor and accretor
the relation between M2 and M˙ based on Porb and q = M2/M1. structural constraints, along with other system proper-
The lower limiton each curve is set byour T =0 M-Rrelations, ties, in Table 1. For those systems in which He disk
the upper limit by the requirement that M1 ≤1.4M⊙. For some stability arguments provide stronger limits, we provide
systems, the accretion disk’s thermal stability, inferred from the
system’s photometric behavior, further constrains M˙. The bold these limits in Table 2. These represent the first limits
lineswitharrowsindicatesuchupperandlowerlimitswhereappli- placed on the donor’s specific entropy in AM CVn sys-
cable(forclarityweshowonlyonearrowforAMCVnandHPLib tems. Again, given current observations, most of these
whichsharealowerdisk-setM˙ limit). Thecirclesalongeachsolid limits are not strong. However, the lower limits on AM
lineindicatewhereourdonormodelshaveTc=105,106, and107 CVnandHPLibsetbydiskstabilityargumentsindicate
K(fromlefttoright).
their donors are far from being T = 0 objects. In V803
Cen, the donor has a maximum T ≈ 106 K, placing it
c
onthe degeneratebranchofthe M-Rrelations. Perhaps
this provides evidence that V803 Cen formed through
set by q and the requirement that M1 < 1.4M⊙, the theWD-channel; however,abetterunderstandingofthe
Chandrasekhar mass. The relations described by the
range in the donor’s initial specific entropy in each for-
solid lines only depend on the donor model through n
mationchannelis neededto supportsuchaclaim. Com-
in equation (3). For M2 < 0.1M⊙, DB03 show that bined with stronger observational limits on other AM
n varies by ≈ 5% between He models with T = 0
c CVn systems, connections between the formation chan-
and T = 107 K. Hence, these M˙ -M relations are only
c 2 nel and the donor’s specific entropy could provide one
weakly dependent on the donor model. Between these
tool for determining a system’s prior evolution.
limits, each system has a potential spread in M of a
2
factor of about 3. The exception is V803 Cen, whose 4. AMCVNSYSTEMSFORMEDTHROUGHTHEWD
very small q sets a minimum whose accretor mass of CHANNEL
M1,min ≈ 1.3M⊙, so that M2 has an extremely narrow We have shown that the AM CVn binaries can oc-
allowed range: 0.021M⊙ ≤ M2 ≤ 0.022M⊙. However, cupy a larger region of M˙ -Porb parameter space than
since there is some uncertainty in the identification of previously thought. There remains the question, how-
P andthesuperhumpperiodinV803Cen(Kato et al. ever, of how much of this parameter space they ac-
orb
2004), and therefore in the derived q, for this system, tually occupy given reasonable evolution scenarios. In
theseconstraintsshouldbeconsideredtentative. Forthe the WD channel, variations in M and in the time the
2
other systems, roughly half (HP Lib, CR Boo, CP Eri, donorhastocoolbeforeitmakescontact,t ,produces
cont
and GP Com) have M1,min > 0.5M⊙, indicating that donors with different initial specific entropies. Figure 3
the accretorcouldbe a C/OorHybrid(Iben & Tutukov showed how this can lead to a wide range of evolution-
1985) WD. However,since M may have grownas much ary tracks. In the He-star channel, the donor initiates
1
as ≈ 0.1−0.2M⊙ during the AM CVn phase, the pos- mass transfer as a He-burning star and its structure de-
sibility the accretor in these systems is a He WD is not pends on M and the amount of He burned to C/O. If
2
ruled out. the composition was fixed, then there would be a sin-
Observations place further constraints on M in some gle M-R relation (the He-burning main-sequence) and
2
of these systems. There is an observed correlation be- all systems would have the same minimum P and the
orb
tweenthephotometricbehaviorofAMCVnsystemsand same subsequent evolution, modulo the variations due
their P . The short period systems, AM CVn and HP to a range in M (up to a factor of 5). However, vari-
orb 1
Lib, are bright and do not exhibit large amplitude vari- ations in t impact how much He is processed before
cont
ability(Warner1995;Solheim et al.1998;Skillman et al. nuclear reactions are quenched by mass loss, affecting
1999). The intermediate period objects—CR Boo, KL the donor’s M-R relation, the binary’s minimum P ,
orb
Dra, V803 Cen, and CP Eri—exhibit large amplitude andproducingvariationinthesubsequentevolutiondur-
variability(≈3-4magnitude;Wood et al.1987;Schwartz ing the AM CVn phase. Our current models cannot ac-
6 Deloye, Bildsten, & Nelemans
Table 1. AM CVn System Parameters with Limits Set by Donor and
Accretor StellarStructure
System Porb (s) Psh (s) q (cid:16)MM2,m⊙in(cid:17)a (cid:16)MM1,m⊙in(cid:17) log(cid:16)M⊙My˙r−1(cid:17) log(cid:16)Tc,Kmax(cid:17) References
AMCVn 1029 1051 0.087 0.035 0.40 -9.43–-8.01 7.48 Nelemansetal.(2001a)
Skillmanetal.(1999)
Solheimetal.(1998)
HPLib 1103 1119 0.056 0.032 0.625 -9.49–-8.46 7.28 Pattersonetal.(2002)
CRBoo 1471 1487 0.042 0.023 0.547 -10.12–-9.09 7.10 Provencaletal.(1997)
Woodetal.(2002)
Pattersonetal.(1997)
KLDra 1502 1533 0.081 0.022 0.277 -10.37–-8.47 7.40 Woodetal.(2002)
V803Cen 1612 1619 0.016 0.021 1.29 -10.12–-10.02 5.95 Pattersonetal.(2000)
CPEri 1701 1716 0.03 0.019 0.641 -10.46–-9.46 6.98 Patterson(2001)
GPCom 2794 ··· 0.022b 0.010 0.46 -11.66–-10.50 6.70 Marsh(1999)
CE-315 3906±42 ··· 0.0125b 0.006 0.48 -12.47–-11.28 6.48 Ruizetal.(2001)
D.Steeghs, priv. comm.
aLowerlimitsonM2,M1,M˙,andTc aresetbyDB03T =0HeM-Rrelations,upperlimitsbyM1<1.4M⊙.
bDeterminedfromspectroscopy.
Table 2. Limits on AM CVn System Parameters set by He Disk
Stabilitya
System (cid:16)MM2,m⊙in(cid:17)a (cid:16)MM1,m⊙in(cid:17) log(cid:16)M⊙My˙r−1(cid:17) log(cid:16)TKc(cid:17)
AMCVn 0.039 0.45 -9.30–-8.01b 6.38–7.48b
HPLib 0.038 0.677 -9.30–-8.46b 6.52–7.28b
KLDra 0.023 0.282 -10.34–-9.00 5.33–7.22
GPCom ··· ··· -11.66b –-11.14 <6.32
aCalculatedusingTsugawa&Osaki(1997)Hediskthermalstabilitycriteria.
bLimitsetbydonororaccretorstructurallimits;seeTable1.
commodate varying internal composition and so we will butthecentralconditionsofthedonorwillbelargelyun-
only address variability within the WD-channel. We re- changed from their state at the start of the CE phase.
fer the reader to Podsiadlowskiet al. (2002, 2003) and Afterwards, the donor will settle towards a cooling He
Nelson & Rappaport (2003) for discussions of the evolu- WD configuration on its thermal time (≈ 106-107 yr).
tionary variations in AM CVns and other ultracompact In the meantime, it cools and contracts until it makes
binaries formed through the H-depleted main sequence contact at a time t later. The system’s evolution
cont
star channel. through these phases determines the specific entropy of
We now show how a range in t affects the P -M˙ the donoratcontact, andthe distribution ofthe donor’s
cont orb
distributionofWD-channelAMCVnsystems. Webegin specificentropyatcontactdeterminesthenumberofsys-
with the population synthesis data fromNelemans et al. tems evolving along a specified range of adiabatic tracks
(2001b). We refer the reader to Nelemans et al. (2001b) (see Figure 3) during the subsequent AM CVn phase
andreferencesthereinforthedetailsoftheirmodel. The and, hence, the resulting population distribution. For
informationneeded for our calculationare the initial ac- donors with M2 ≈ 0.01−0.03M⊙, as is appropriate for
cretoranddonormasses,M andM ,atthebeginning the known AM CVns, it is the specific entropy of the
1,i 2,i
of the AM CVn stage, t , and the galaxy’s age when inner ≈ 10% of the initial donor mass that matters for
cont
the system begins the AM CVn stage. We use t to current the evolution. We thus emphasize a proper ac-
cont
determine the donor’s specific entropy at contact using countingofthedonor’scentralconditionsthroughoutthe
existing He WD evolution calculations. We evolve each pre-contact evolution to ensure we calculate a realistic
systemadiabaticallyfromcontactassumingconservative population distribution for P &20 min.
orb
mass transfer driven by GW emission up to the present To determine the initial donor model, we begin by de-
ageofthegalaxy(takentobe10Gyrs)inagreementwith terminingthecentralconditionsinthedonor’sprogenitor
Nelemans et al.(2001b). WeremovedsystemswhereM at the time the CE phase begins. The Nelemans et al.
1
grew larger than 1.4 M⊙ during this evolution. (2001b)datagivestheprogenitor’sageandHecoremass
(M ) at this time. These two quantities constrain the
2,i
4.1. Determining the Initial Donor Model progenitor’s initial mass. We use the EZ stellar evolu-
tion code (derived from Peter Eggleton’s stellar evolu-
The donor starts out as the core of a red giant branch
tion code; see Paxton 2004, and references therein) to
star which initiates unstable mass transfer and a CE
calculate ρ , T in a star of this initial mass and age.
phase. The state of the outer regions of the donor af- c c
The central conditions in the donor do not change dur-
tertheCEphaseends(e.g.,howmuchofaHenvelopeis
ing the rapidCE phase and we use the ρ , T just found
left)willdependontheuncertaindetailsofCEevolution, c c
Arbitrarily Degenerate Donors in AM CVn Systems 7
to determine the initial conditions for the WD cooling and the isentropic donors have the most compact con-
phase. To calculate the WD cooling, we use the pure- figuration for a given central specific entropy. Therefore
He WD cooling models of Althaus & Benvenuto (1997) our results provide a lower limit on the impact of finite
(hereafter AB97). For a given WD mass, these models T on the WD-channel AM CVn population.
c
do not necessarily have a (ρ , T ) pair matching that The uncertainties associated with the CE phase and
c c
just found for the core (due to differences in the interior the subsequent He WD cooling phase lead to uncertain-
profile between the two models). We map from the core ties in R near contact. While this clearly impacts the
2
model to the WD cooling model by fixing ρ and M , shortperiodAMCVndistribution,itmayalsobesignif-
c 2,i
which then determines T for the cooling model. While icanttotheoverallpopulation. DonorswithlargerR at
c 2
thisisanadhocmethodology,withoutbeingabletocal- contact—as expected for hotter, isothermal donors—are
culate the thermal evolution of the donor relaxing from notaslikelytoexperienceamasstransferinstabilitydue
its post-CE configuration to the WD configuration it is toadvectionofangularmomentumontotheaccretor(ei-
difficult to argue for a more accurate prescription. In ther during a direct-impact accretion phase or because
any case, the change in central specific entropy involved the accretiondisk atshortperiods hasasmallradialdy-
in this mapping is usually small compared to the en- namic range; Nelemans et al. 2001b; Marsh et al. 2004).
tropy lost during the cooling. We then use t and the Taking account of this effect could, therefore, increase
cont
AB97coolingsequencestodeterminethe donor’scentral the number of WD-channel systems that survive to be-
conditions at contact. Finally, to determine the start- come AM CVn binaries (as well as the upper limit on
ing AM CVn evolution model, we find the DB03 model M in those that do).
2
with M = M and a specific entropy that equals the
2 2,i 4.2. The Resulting Population
central specific entropy of the AB97 model at contact.
Generallyspeaking,mostdonorsmakecontactas mildly We now compare the WD-channel population calcu-
to extremely degenerate objects, but there is a fraction lated using the DB03 T = 0 M-R relations with the
of non-degenerate donors in the population. Once the onecalculatedtakingintoaccountthe pre-contactdonor
initial model is determined, we calculate a from the re- cooling. We will refer to these two populations as the
quirement that R = R at contact and integrate the T = 0 and RWDC (realistic WD cooling) populations,
L 2
system’sevolutionwithM˙ calculatedfromequation(3). respectively. This T =0 population differs slightly from
WecalculateP fromequation(2)andnfromourmod- theanalogousresultsofNelemans et al.(2001b),astheir
orb
els assuming adiabatic evolution. fully degenerate M-R relation differs from DB03. In
While providing a reasonable estimate of the central the M2 range of interest, the Nelemans et al. (2001b)
conditions inthe donor’score,this prescriptiondoes not donors are more compact than DB03’s so that the re-
allow us to determine the evolution of the donor’s outer sultingM˙ (P )relationfromtheDB03donorsisshifted
orb
regions prior to contact. This will impact the evolution upwardby≈10−20%fromthatforthe Nelemans et al.
of these AM CVn systems at short P . For example, (2001b)donors. IntheRWDCpopulation,thetrackeach
orb
R (atfixedT andM )issmallerinourisentropicmod- system follows is determined by the donor’s specific en-
2 c 2
els than in the thermal equilibrium AB97 models, as is tropy at contact, with the relative number of systems
expected. If we were to take the AB97 model’s R at evolving along each adiabat determined by the distri-
2
contact instead of the DB03 R , the initial P would bution in t . In the Nelemans et al. (2001b) data ≈
2 orb cont
increasebyuptoafactorof2-3,dependingonthedonor’s 10%,30%,and70%ofthesystemshavet ≤100Myr,
cont
degeneracy. Additionally, using isentropic donors post- 500Myr,and1Gyr,respectively,producingasignificant
contact produces a different evolution than obtained by fraction of systems not evolving along the T = 0 track.
self-consistently evolving the structure of the donor at Since these numbers are based on using T = 0 radii for
contact (something we are not able to do with our cur- the pre-contact donor, they are a lower limits to a self-
rentmodels). Thediscrepancybetweenthetwoevolution consistentlydetermineddistributionoft ,wheremore
cont
tracks should grow smaller as the donor loses mass and systemswouldhavehotterdonorsatcontact. Thedistri-
only the central regions of the star matter. bution of t also depends onthe assumptions made in
cont
Other factors also create uncertainty in the evolution calculatingtheCEphase. AlargerCEefficiencyparame-
during the early AM CVn phase. The cooling rate of a ter(theratioofthechangeinenvelopebindingenergyto
He WD depends on the amount of H left in its envelope changes in orbital energy) than used by Nelemans et al.
after the CE event and whether H/He diffusive mixing (2001b), forexample,wouldproducesystemswithwider
is considered or not (Driebe et al. 1999; Althaus et al. separations at the end of the CE phase and reduce the
2001; Althaus & Benvenuto 1997; Benvenuto & Althaus number of systems with hot donors.
1998; Sarna et al. 2000). The amount of H that remains Figure 5 shows the distribution of AM CVn binaries
after the CE is uncertain (see, e.g., Iben & Livio 1993). versusP inthetwopopulations. Bothexhibit,atfirst,
orb
In general, more H leads to slower WD cooling due to therapidincreaseinthenumberofsystemswithincreas-
its greater opacity and the possible residual H burning ingP duetotheincreaseinbinaryevolutiontimewith
orb
in the lower atmosphere. Further uncertainty is added P . The T = 0 population (dot-dashed lines in Figure
orb
by the questions of whether strong shell flashes can oc- 5) has a sharp cut-off at P ≈ 80 min set by how far
orb
cur (Driebe et al. 1999; Sarna et al. 2000; Althaus et al. a T = 0 donor can evolve in 10 Gyr. Hot donors make
2001), altering the subsequent cooling rates by rapidly contact at, and evolve out to, longer P than fully de-
orb
consuminglargeamountsofH.Allofthisleadstosignif- generate ones. The range in the donor’s specific entropy
icantuncertaintyintheAMCVnpopulationdistribution inthe RWDCpopulationthereforepreventsasharpcut-
at short P . However, pure He WDs cool the fastest off in systems above P ≈ 80 min. Instead there is a
orb orb
factor of ≈ 20 decrease between the number of systems
8 Deloye, Bildsten, & Nelemans
Fig. 6.— The distribution of systems in M˙ at the approxi-
mate Porb of AM CVn and CE-315. Our RWDC population is
shownbythesolidline,theT =0populationisshownbythedot-
dashedline,andtheNelemansetal.(2001b) T =0resultsbythe
Fig. 5.—Ahistogramofthenumberofsystemsasafunctionof dotted lines. A comparison between the Nelemansetal. (2001b)
Ppoorpbulbaettiownese.ntThheeTh=igh0e(rdsopt-edcaifischeedntlirnoep)yaonfdsRoWmeDCdo(nsoorlsidinlintehse) pshoipftuliantitohneaM˙nddiosutrribTu=tio0npporopduulacteidonbyshtohwesdtihffeermenacgenbiteutdweeeonftthhee
RWDCpopulationleakssystemstowardslongerorbitalperiodsas Zapolsky&Salpeter(1969)M-Rrelationandour,moreaccurate,
compared to the T =0 population. The smooth curves show the T = 0 relations. The existence of hotter donors in the RWDC
percentage of each population lying above a given Porb. In the produces the tail seen in that population’s M˙ distribution. At
RWDC population, 65% of systems have Porb > 60 min (50% of the longer Porb of CE-315, the spread in M˙ increases as specific
the T = 0 population lies above this period); 10% of the RWDC entropy differences have more a significant impact on lower-mass
populationliesabovetheT =0population’sPorb≈80mincutoff. donor’sstructure.
at P = 80 and the number at P = 100 min in the
orb orb larpopulationsynthesis calculationusedhere to provide
RWDC population. The overall result is a shifting of
the initial conditions. The number of systems in the tail
systems from shorter to longer P in the RWDC pop-
orb of the distribution increases with P , as a higher spe-
orb
ulation as compared to the T = 0 population, resulting
cificentropyhasamoresignificantimpactonthedonor’s
in a reduction in the number of systems we expect to
structure at lower M . The majority of systems in the
2
see in the P range of the known AM CVn population
orb RWDC population lie near the T = 0 tracks as is ex-
(i.e. Porb < 65 min). In the RWDC population, 65 % pected, but ∼ 10% of this population have donors that
of systems have P > 60 min, while 50% of the T = 0
orb produce mass transfer rates greater than the spread at-
populationliesabovethisperiod;10%oftheRWDCpop-
tributabletoM variationsalone(atleastatlongerP ;
1 orb
ulation lies above the T =0 population’s P =80 min
orb see the right hand panel in Figure 6 in particular).
cut-off.
The range in M˙ that AM CVn binaries can attain at 4.3. Implications for the AM CVn Gravity Wave Signal
fixed P is increased in the RWDC population. Fig-
orb
ure 1 shows that at fixed P , hotter donors must be The galactic population of AM CVn binaries con-
orb
more massive. As M˙ ∝ M2/3M2 (at fixed P and tains objects that can be detected with the planned
2 2 orb Laser Interferometer Space Antenna (LISA) gravity
when M ≪M ), hotter donors lead to a larger M˙ (see
2 1 wave detector mission (see http://lisa.nasa.gov/ and
also Figure 2). We show in Figure 6 the distribution
http://sci.esa.int/home/lisa/ for mission details), and
of the AM CVn WD-channel population M˙ ’s at the or- the gravity wave signal of the AM CVn binary pop-
bital periods of AM CVn, and CE-315 in the T =0 and ulation has been considered in several recent stud-
RWDC populations. In addition, we also show the re- ies (Nelemans et al. 2001c; Farmer & Phinney 2003;
sults obtained with the Nelemans et al. (2001b) T = 0 Nelemans et al. 2004). Here we discuss the differences
M-R relation to indicate the magnitude of the shift in betweentheT =0andRWDCpopulations’gravitywave
M˙ produced when using our more accurate T = 0 re- signals.
lation. The M˙ range in the T = 0 populations is due Abinarysysteminacircularorbitemitsgravitywaves
to the range in M1 at each Porb. In the RWDC pop- at a frequency f = 2/Porb (i.e. twice the orbital fre-
ulation, the existence of higher entropy donors leads to quency) and luminosity, LGW, (Press & Thorne 1972)
systems with larger M at a given P and the tail to-
2 orb 32G4M2M2(M +M )
wards higher M˙ seen in this distribution. The offset in L = 1 2 1 2 , (5)
theminimumM˙ seenbetweentheT =0andtheRWDC GW 5 c5 a5
populationresultsfromthefactthatforthelowestaccre- where G is the gravitationalconstant and c the speed of
tor masses in the RWDC population, none have donor’s light. The flux, F = L /4πd2, received by a detector
GW
that are close to fully degenerate. It is unclear if this is a distance, d, from the source is often written in terms
a robust result or simply a consequence of the particu- of the so-called dimensionless strain amplitude, h, given
Arbitrarily Degenerate Donors in AM CVn Systems 9
massive, increasing M.
The integrated GW flux from a collection of identical
AMCVnbinariesdependsonthedonor’sspecificentropy
in two ways. First, the flux from each system at a fixed
f increases with the donor’s specific entropy. Second,
eachsystem’sf˙=df/dtdependsonn,whichvarieswith
boththedonor’smassandspecificentropy. Forconstant
n in a steady-state population, one can derive a simple
scaling for the GW energy density per logarithmic fre-
quency interval, E ∝ fN(f)L (f) ∝ fL (f)/f˙
GW GW GW
= fdE /df. This can be expressed in terms of the
GW
dimensionless characteristic amplitude in a logarithmic
interval, h , as
c
πf2c2
E = h2(f). (7)
GW 4G c
Taking R ∝ Mn, and assuming M ≪ M along with
2 2 2 1
stable mass transfer, h2 ∝fα where
c
2+12n
Fig. 7.— An AM CVn binary’s (with M1,i = 0.6M⊙, α= 3(1−3n), (8)
M2,i = 0.2M⊙ at 1 kpc) h versus Porb, showing the impact of
a hot donor on the system’s post-contact GW flux. The dashed
(seePhinney2001;Farmer & Phinney2003,foraderiva-
line shows the system’s pre-contact inward evolution, the sym-
bols showing when its time to contact (for a T = 0 donor) is tionofthis under the assumptionn=−1/3). Returning
log(t/yr)=5.0,5.5,6.0,6.5,and7.0, lefttoright. Thesolidlines to Figure 7, at contact n = −0.350 for the fully de-
showthe post-contact evolutionforaT =0donor andfordonors generate donor, while for the donor making contact at
hot enough to make contact at Porb = 5(10) min. The symbols 5 min (10 min) , n = −0.342 (-0.333). At P = 20
hereshowtimesincecontact: log(t/yr)=5.0,5.5,6.0,6.5,7.0and orb
7.5,lefttoright. AtfixedPorb,hotterdonorsaremoremassiveand min (f = 1.67×10−3 Hz), the three donors have n =
louderGWsources. Thedottedlineshowsthedetached WD-WD −0.233,−0.276, and −0.308 respectively. As α is an in-
binaryconfusionlimitforLISA(Nelemansetal.2001c). creasing function of n and is negative for n < −0.167,
h2 falls off less rapidly with f for cold donors (as they
c
evolve less rapidly in f than donors with higher specific
by (Press & Thorne 1972; Nelemans et al. 2001c) entropy). WhilehotterdonorsproduceAMCVnbinaries
thatareindividuallymoreGWluminousatfixedf,their
4G 1/2
h= F increasedrate of f evolution somewhat mitigates this in
(cid:20)c3πf2 (cid:21) the population’s overallGW energy density at lower f.
M 5/3 P −2/3 d −1 We now move from these simple analytics to a di-
=5.0×10−22 orb , rect numeric calculation of the GW signal from both
(cid:18)M⊙(cid:19) (cid:18) hr (cid:19) (cid:18)kpc(cid:19) the T = 0 and RWDC populations. We begin, follow-
(6) ing Nelemans et al. (2001c), by randomly distributing
the systems in each population in galactic coordinates
where M = (M M )3/5/(M +M )1/5 is known as the
1 2 1 2 with uniform probability in galactic azimuth and with a
chirp mass. In an individual AM CVn binary, changing
probability,P(R , z),ingalacticradius,R ,andheight
the entropy of the donor changes the relation between G G
above the mid-plane, z of
M and P and alters the binary’s GW luminosity. We
orb
showa summary ofhow hotdonorschangethe expected 1 R z 2
GW signal in Figure 7, where we consider the evolution P(RG, z)= 2H2β exp(cid:20)− HG(cid:21)sech(cid:18)β(cid:19) , (9)
of an AM CVn binary with M1,i = 0.6M⊙ and M2,i =
0.2M⊙ located 1 kpc away. The evolution of this binary where β = 200 pc and H = 2.5 kpc. To calculate d
pre-contact is independent of the donor’s state, and the for each system we took the position of the sun to be
system’shasafunctionofP evolvesinwardalongthe R = 8.5 kpc and z = −30 pc, again following
orb sun sun
dashed line in Figure 7 toward shorter periods. If the Nelemans et al. (2001c). We then calculated h for each
donor is fully degenerate, the binary makes contact at system from its d and current orbital parameters using
P ≈ 3.5 min and then evolves outward in P along equation(6). Figure8presentstheresultingdistribution
orb orb
the left-most solid line. The orbital period at contact of AM CVn binaries in f and h for each of these popu-
depends on the donor’s entropy. The other two solid lations. As expected, the qualitative difference between
lines show the evolution for systems making contact at theT =0(lowerpanel)andRWDC(upperpanel)distri-
P = 5 min (requiring a partially degenerate donor butions is a shift in individual systems to lower f in the
orb
withT =5.6×107Katcontact)and10min(requiringa RWDC population with an extended tail in the RWDC
c
non-degeneratedonorwith T ≈6.1×107 K atcontact), distributiontofrequencieslowerthanf ≈4.0×10−4Hz.
c
respectively. Donors with these entropies occur in the The fraction of this AM CVn population that LISA
RWDC population (which contains systems that make will detect is set by LISA’s sensitivity and the galactic
contact at orbital periods as large as ≈ 25 min). The populationofdetachedWD-WDbinaries. Forasignalto
qualitative impact of a hot donor is the increase in h as noise (S/N) ratios of 1 and 3, LISA’s predicted sensitiv-
afunctionofP ashotterdonorsatfixedP aremore ity (as calculated with Shane Larson’s online generation
orb orb
10 Deloye, Bildsten, & Nelemans
P (min) P (min)
orb orb
102 101 102 101
4
200
--222222 -2222 180
3 160
-2233
--222333 140
120
h) h) -2244
log( 2 log( 100
--2222 -2222 80
60
1
--2233 -2233 40
20
-2244
0 0
-3.5 -3 -2.5 -2 log(N) -3 -2.5 -2 N
log(f/Hz) log(f/Hz)
Fig. 8.— The distribution in the galactic population of WD- Fig. 9.—ThedistributionofLISAresolvedsystemsintheRWDC
channel AM CVn binaries in h and f for the RWDC (upper (upperpanel)andT =0(lowerpanel)populations. Thegrey-scale
panel) and T = 0 (lower panel) populations. The grey-scale in- indicatesthetotalnumberofsourcesineach(f,h)bin. Thesolid
dicatesthelogarithmoftotalnumberofsourcesineach(f,h)bin. gray line shows the confusion limit calculated by Nelemansetal.
The solid line shows the WD-WD confusion limit calculated by (2001c), while the dotted line shows LISA’s predicted sensitivity
Nelemansetal. (2001c), while the dotted lines shows LISA’s pre- for a S/N ratio of 1 (lower line) and 3 (upper line) (Larsonetal.
dicted sensitivity for a S/N ratio of 1 (lower line) and 3 (upper 2000,2002).
line)(Larsonetal.2000,2002).
cludedinourcalculationwillalsocontributetotheLISA
signal;as we are interested here in how a range in donor
script, http://www.srl.caltech.edu∼shane/sensitivity/,
specificentropyimpactsthe WD-channelpopulation,we
based on the results of Larson et al. 2000, 2002) is
ignorethisaddedcomplication). BetweentheT =0and
shown by the dotted lines in Figure 8. Popula-
RWDC populations, the distribution of LISA resolvable
tion synthesis studies indicate that detached WD-
sourcesdiffersslightly,asweshowinFigure9. Themain
WD binaries will dominate the GW signal at fre-
quencies f . 10−3 Hz (Evans, Iben, & Smarr 1987; differencebetweenthetwodistributionsistheslightshift
in the maximum of the RWDC population relative to
Lipunov et al. 1987; Hils et al. 1990; Nelemans et al.
that of the T = 0 and a decrease in the total number
2001c; Farmer & Phinney 2003). These systems are ex-
of resolved systems. This is seen more clearly in Fig-
pected to produce a so-called “confusion limit”, a noise
ure 10 were we show the histogram of resolved systems
background below ≈ 2 mHz produced by the vast num-
in each population versus f. Overall, the RWDC pop-
ber of systems that will not be individually resolvable.
ulation contains ≈ 6% fewer resolved systems than the
The solid lines in Figure 8 shows the confusion limited
T = 0 and the RWDC distribution’s mean frequency is
noise set by this background (essentially the averaged
≈ 10−4 Hz less than the T = 0’s. As compared to the
GW signal from detached WD-WD binaries) as calcu-
results for the fully degenerate distribution calculated
lated by Nelemans et al. (2001c). The WD-channel AM
using the Nelemans et al. (2001b) degenerate M-R rela-
CVns in the T = 0 population that will be detectable
tions, the RWDC contains ≈11% fewer systems.
above both the LISA sensitivity curve and the confu-
sion limited noise have an average d of 8.6 kpc. The
4.4. Future Calculation Refinements
corresponding RWDC population contains ≈ 13% fewer
systems at an average d of 8.7 kpc. The decrease in These population calculations are only a first step to-
the RWDC numbers is due mainly to the shifting of sys- wards a more realistic theoretical treatment of the AM
tems towards shorter f. Even though individual RWDC CVn population. Here we speculate on the possible re-
systems are on average louder than the T = 0 systems, sults of a more refined calculation. In particular, how
the volume over which LISA will detect these systems would improving on the approximations necessitated by
is not significantly altered. This is due to the fact most our current donor models alter our result? The choice
of the AM CVn systems above the confusion limit in ei- of adiabatic evolution assumes that the donor cools on
ther population are detectable to the edge of the galaxy a time scale long compared to the mass loss time scale
(the galacticgeometrysetsthe lowerrightcutoffofboth (∼ M /M˙ ). While this is almost certainly the case for
2
distributions in Figure 8). systemsnear contact,it maynot be the case forsystems
For an estimated mission length of 1 yr, LISA will be atlongP . Ifandwhenadiabaticityisviolateddepends
orb
able to resolve frequencies separated by ∆f ≈ 1/1yr = onhow the donor’sluminosity scales with T andM . If
c 2
3 × 10−8 Hz. AM CVn binaries with an h above the adiabatic evolution doesn’t hold, then some fraction of
confusionlimitednoiseandthataretheonlysystemina the long P systems in the RWDC population could
orb
givenresolvedfrequencybinwillbeindividuallyresolved drop out of the AM CVn population as the donor cools
byLISA(this isabitofanoversimplificationsinceother and contracts within its Roche Lobe, reducing the num-
populations, such as detached WD-WD binaries, not in- ber of expected long period AM CVn systems. Whether