
Approximation spaces, limiting interpolation and Besov spaces PDF
Preview Approximation spaces, limiting interpolation and Besov spaces
UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS MATEMÁTICAS Departamento de Análisis Matemático TESIS DOCTORAL Espacios de aproximación, interpolación límite y espacios de Besov (Approximation spaces, limiting interpolation and Besov spaces) MEMORIA PARA OPTAR AL GRADO DE DOCTOR PRESENTADA POR Óscar Domínguez Bonilla Directores Fernando Cobos Díaz Antonio Martínez Martínez Madrid, 2017 © Óscar Domínguez Bonilla, 2016 Universidad Complutense de Madrid Facultad de Ciencias Matemáticas Departamento de Análisis Matemático Espacios de aproximación, interpolación límite y espacios de Besov (Approximation spaces, limiting interpolation and Besov spaces) Memoria para optar al grado de doctor con mención de Doctorado Europeo presentada por Óscar Domínguez Bonilla Bajo la dirección de los doctores Fernando Cobos Díaz y Antonio Martínez Martínez Madrid, 2016 Agradecimientos Quisiera mostrar mi agradecimiento a todas aquellas personas que me han ayudado en la realización de este proyecto. En primer lugar, mis directores de tesis, Fernando Cobos Díaz y Antón Martínez Martínez, por sus consejos que han sido mi guía en estos años. Va también mi gratitud a todos los miembros del Departamento de Análisis Matemático de la Universidad Complutense de Madrid. Quisiera también expresar mi agradecimiento al Department of Mathematics and Computer Science de Friedrich- Schiller-Universität Jena por su calurosa bienvenida y trato recibido. Por último, gracias a mi familia por su constante apoyo. Sobre esta memoria El desarrollo de esta memoria ha sido posible gracias a la Beca de Formación de ProfesoradoUniversitario(FPU)dereferenciaAP2012-0779concedidaporelMinisterio de Educación. Además, participé entre abril de 2013 y diciembre de 2014 como miembro del equipo investigador del proyecto de título Interpolación, Espacios de Funciones y Aplicaciones de referencia MTM2010-15814 financiado por el Ministerio de Ciencia e Innovación, y desde enero de 2015 como miembro del equipo de trabajo del proyecto de título Inter- polación, Aproximación, Entropía y Espacios de Funciones de referencia MTM2013- 42220-P financiado por el Ministerio de Economía y Competitividad. A lo largo de estos cuatro años, he podido realizar una estancia de investigación en la universidad Friedrich-Schiller-Universität de Jena (Alemania) bajo la supervisión del Profesor H.-J. Schmeisser. Dicha estancia fue subvencionada por la beca FPU AP2012-0779 del Ministerio de Educación y durante su transcurso, pude ampliar mis conocimientos y trabajar junto con un grupo de referencia internacional como es el grupo “Funktionenräume". Fruto del trabajo de estos cuatro años son los artículos - F. Cobos, O. Domínguez, Embeddings of Besov spaces of logarithmic smoothness, Studia Math. 223 (2014), 193–204. - F. Cobos, O. Domínguez, Approximation spaces, limiting interpolation and Besov spaces, J. Approx. Theory 189 (2015), 43–66. - F. Cobos, O. Domínguez, On Besov spaces of logarithmic smoothness and Lipschitz spaces, J. Math. Anal. Appl. 425 (2015), 71–84. - F. Cobos, O. Domínguez, On the relationship between two kinds of Besov spaces with smoothness near zero and some other applications of limiting interpolation, J. Fourier Anal. Appl., DOI 10.1007/s00041-015-9454-6, published online: 29 December 2015. - F. Cobos, O. Domínguez, On Besov spaces modelled on Zygmund spaces, preprint, Madrid, 2015. - F. Cobos, O. Domínguez, A. Martínez, Compact operators and approximation spaces, Colloq. Math. 136 (2014), 1–11. - F. Cobos, O. Domínguez, H. Triebel, Characterizations of logarithmic Besov spaces in terms of differences, Fourier-analytical decompositions, wavelets and semi-groups, J. Funct. Anal. (2016), http://dx.doi.org/10.1016/j.jfa.2016.03.007. - O. Domínguez, Tractable embeddings of Besov spaces into small Lebesgue spaces, Math. Nachr., DOI 10.1002/mana.201500244, published online: 25 January 2016. Contents Resumen 9 1 Introduction 19 2 Preliminaries 29 2.1 Basic approximation constructions . . . . . . . . . . . . . . . . . . . . . . . 30 2.2 Interpolation methods. Some interpolation formulae. Extrapolation spaces 33 2.3 Besov spaces. Characterization by approximation . . . . . . . . . . . . . . 42 3 Reiteration of approximation constructions 47 3.1 Reiteration formulae . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 3.2 Applications to Besov spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 4 Compact operators and approximation spaces 63 4.1 Compact operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 7 8 CONTENTS 5 Embeddings of Besov spaces of logarithmic smoothness 71 5.1 Embeddings of Bα,b(T) into Lorentz-Zygmund spaces . . . . . . . . . . . . 73 p,q 5.2 Embeddings between Besov spaces with smoothness close to zero . . . . . 83 5.3 Embeddings between Besov spaces with different metrics . . . . . . . . . . 93 5.4 Embeddings between Besov and Lipschitz spaces . . . . . . . . . . . . . . . 94 6 Some other applications of limiting interpolation 99 6.1 Duality . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 6.2 Fourier coefficients . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101 6.3 Derivatives on Besov spaces B0,−1/q(T) . . . . . . . . . . . . . . . . . . . . . 105 p,q 7 Tractable embeddings of Besov spaces into small Lebesgue spaces 107 7.1 Extrapolation description of small Lebesgue spaces . . . . . . . . . . . . . 108 7.2 Tractable embeddings of classical Besov spaces . . . . . . . . . . . . . . . . 117 7.3 Tractable embeddings of Besov spaces with logarithmic smoothness . . . 123 8 Besov-Zygmund spaces and logarithmic Besov spaces 127 8.1 Spaces Bs(L (logL) ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128 p p b 8.2 Relation with spaces Bs,b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135 p,p 8.3 Embeddings into C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 9 Equivalent characterizations of B0,b 141 p,q 9.1 Characterization of B0,b by differences . . . . . . . . . . . . . . . . . . . . . 142 p,q 9.2 Characterization of B0,b by approximation and limiting interpolation . . 143 p,q 9.3 Fourier-analytical decomposition of B0,b . . . . . . . . . . . . . . . . . . . . 145 p,q 9.4 Characterization of B0,b in terms of wavelets . . . . . . . . . . . . . . . . . 152 p,q 9.5 Semi-groups of operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163 Bibliography 173 Resumen En esta memoria profundizamos en la conexión entre espacios de aproximación y méto- dos límites de interpolación, aplicando los resultados a problemas en espacios de fun- ciones y, en particular, en espacios de Besov. La relación simbiótica entre teoría de aproximación y teoría de interpolación es bien conocida como se puede ver en los libros de Bergh y Löfström [10], Triebel [116], Petrushev y Popov [103] y DeVore y Lorentz [50]. El método de interpolación real (A ,A ) juega un papel importante en este asunto. Se introduce principalmente por 0 1 θ,q medio del K-funcional de Peetre K(t,a)=K(t,a;A ,A )=inf{∥a ∥ +t∥a ∥ ∶a=a +a ,a ∈A },a∈A +A . 0 1 0 A0 1 A1 0 1 j j 0 1 Normalmente 0 < θ < 1 pero para cubrir algunos casos extremos, versiones límites han sido también empleadas, donde θ = 0,1 y pesos logarítmicos pueden ser incluidos. Ver los artículos de Gomez y Milman [72], Evans y Opic [61], Evans, Opic y Pick [63], Cobos, Fernández-Cabrera, Kühn y Ullrich [33], Cobos y Kühn [40] y Edmunds y Opic [58]. Dado un espacio cuasi Banach X y una familia de aproximación (G ) de sub- n n∈N0 conjuntos de X, los espacios de aproximación Xα se definen seleccionando aquellos p elementos f ∈X tales que (nα−1/pE (f)) pertenece a (cid:96) . Aquí los parámetros cumplen n p que 0 < α < ∞ y 0 < p ≤ ∞ y E (f) = inf{∥f −g∥ ∶ g ∈ G } es el error de mejor n X n−1 aproximación de f por elementos de G (ver Sección 2.1 para mayores detalles). Estos n−1 espacios han sido estudiados por Butzer y Scherer [16], Pietsch [104, 105], Petrushev y Popov [103], y DeVore y Lorentz [50], entre otros autores. Los espacios de aproximación límite X(0,γ) se definen haciendo α=0 e insertando el peso (1+logn)γ con la sucesión q (E (f)). Han sido investigados por Cobos y Resina [44], Cobos y Milman [41], Cobos n y Kühn [38], Fehér y Grässler [65] y las referencias dadas en estos artículos. Como fue probado en [44], incluso cuando γ = 0, la teoría de los espacios de aproximación 9
Description:The list of books you might like

What Happened to You?

The Mountain Is You

The 5 Second Rule: Transform your Life, Work, and Confidence with Everyday Courage

The Silent Patient

IS/ISO 105-A03: Textiles- Tests for colour fastness Part A02- Grey scales for assessing staining (Superseding IS 769

by order of the secretary air force instruction 10-702 of the

Budget-At-A-Glance, 2006-07

The Benko gambit

Bürgerliches Recht II. Schuldrecht Allgemeiner Teil, 3. Auflage
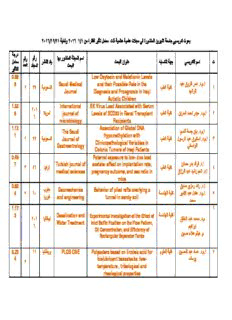
2016 / 12 / 21 ولغاية 2016 1 1

Einstein Product Metrics in Diverse Dimensions
![Verrassing: verliefd! (Wrangler's Creek 02)[Feelgood 18] book image](https://cdn-3.pdfdrive.to/media/content/thumbnails/17318296.jpg)
Verrassing: verliefd! (Wrangler's Creek 02)[Feelgood 18]

Greek Government Gazette: Part 7, 2006 no. 837

Polar Bear: 2006

Glossary

C. J. Cherryh - Union Alliance - Finity' s End

Description of two new species of Nesogobius (Pisces: Gobioidei: Gobiidae) from southern Australia

Greek Government Gazette: Part 3, 2006 no. 388

Jagged Alliance 2

ERIC ED512406: IDRA Newsletter. Volume 37, No. 6




