Anova a 2 vie con repliche PDF
Preview Anova a 2 vie con repliche
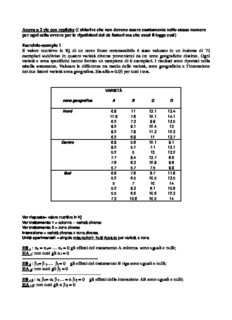
Anova a 2 vie con repliche (( chiarire che non devono essere esattamente nello stesso numero per ogni cella ovvero per le ripetizioni dei de fattori ma che excel li legge così) Esercizio-esempio 1 Il valore nutritivo in Kj di un certo frutto commestibile è stato valutato in un insieme di 72 esemplari suddiviso in quattro varietà diverse provenienti da tre zone geografiche distinte. Ogni varietà e zona specifiche hanno fornito un campione di 6 esemplari. I risultati sono riportati nella tabella sottostante. Valutare le differenze tra medie delle varietà, zone geografiche e l’interazione dei due fattori varietà-zona geografica. Sia alfa = 0.05 per tutti i test. VARIETÀ zona geografica A B C D Nord 6.9 11 13.1 13.4 11.8 7.8 12.1 14.1 6.2 7.3 9.9 13.5 9.2 9.1 12.4 13 9.2 7.9 11.3 12.3 6.2 6.9 11 13.7 Centro 8.9 5.8 12.1 9.1 9.2 5.1 7.1 13.1 5.2 5 13 13.2 7.7 9.4 13.7 8.6 7.8 8.3 12.9 9.8 5.7 5.7 7.5 9.9 Sud 6.8 7.8 8.7 11.8 5.2 6.5 10.5 13.5 5 7 10 14 5.2 9.3 8.1 10.8 5.5 6.6 10.6 12.3 7.3 10.8 10.5 14 Var risposta= valore nutritivo in Kj Var trattamento 1 = colonne – varietà diverse Var trattamento 2 = zone diverse Interazione = varietà diversa x zona diversa Unità sperimentali = singole misurazioni- frutti ripetute per varietà e zona H0 : α = α = … α = 0 gli effetti del trattamento A colonna sono uguali e nulli; α 1 2 i HA : non tutti gli α = 0 α i ------------------------------------------------- H0 : β = β …. β = 0 gli effetti del trattamento B riga sono uguali e nulli; β 1 2 j HA : non tutti gli β = 0 β j --------------------------------------------------- H0 : α β = α β …= α β = 0 gli effetti della interazione AB sono uguali e nulli; α β 1 1 1 2 ij HA : non tutti gli α β = 0 α β ij Numero trattamenti A colonne = k=4; numero trattamenti B righe B = j =3 Numero ripetizioni per interazione trattamento A x trattamento B = n = 6 Gradi di libertà totali =(k*j*n)-1= (4*3*6) -1 = 72-1= 71 Gradi di libertà tra trattamenti A -colonne = k-1 = 4-1= 3 Gradi di libertà tra trattamenti B -righe = j-1 = 3-1 = 2 Gradi di libertà della interazione =( k-1) (j-1)= 3*2 =6 Gradi di libertà della variazione residua-errore =k*j*(n-1)= 4*3*(6-1)= 60 F critico per RV trattamento A colonne : alfa= 0.05, 3 gdl al numeratore / 60 gdl al denominatore = 2.76 F critico per RV trattamento B righe: alfa= 0.05, 2 gdl al numeratore / 60 gdl al denominatore =3.15 F critico per RV interazione fattori colonne-righe: alfa= 0.05, 6 gdl al numeratore / 60 gdl al denominatore = 2.25 ANALISI VARIANZA Analisi Dati Excel Origine della variazione SQ gdl MQ F Valore di significatività F crit Campione-Righe-Zone 31.50694444 2 15.75347 5.478780443 0.00652495 3.150411 Colonne-Varietà 325.5748611 3 108.525 37.74306931 7.82751E-14 2.758078 Interazione 33.17305556 6 5.528843 1.922834169 0.091675558 2.254055 residuo 172.5216667 60 2.875361 Totale 562.7765278 71 Quindi rifiuto H0 rifiutoH0 non rifiuto H0 α, β, α β. Accetto le rispettive HA e HA H0 α β e α β. I risultati indicano che sia le varietà del frutto che le zone di coltivazione hanno un effetto significativo sulla valore nutritivo dello stesso, ma non l’interazione dei due fattori. Con il programma STATA -------------------------------------------------------------------------------- anova varrisposta variet##zona Number of obs = 72 R-squared = 0.6934 Root MSE = 1.69569 Adj R-squared = 0.6372 Source | Partial SS df MS F Prob > F ------------+---------------------------------------------------- Model | 390.25487 11 35.4777155 12.34 0.0000 | variet | 325.574872 3 108.524957 37.74 0.0000 zona | 31.5069453 2 15.7534726 5.48 0.0065 variet#zona | 33.1730526 6 5.5288421 1.92 0.0917 | Residual | 172.521668 60 2.87536114 ------------+---------------------------------------------------- Total | 562.776538 71 7.92643012 --------------------------------------------------------------------------------------- I risultati sono uguali Risoluzione esercizio con il software R (v2.15.1) #Importazione dati data_frutti<-read.csv2(file.choose(), header= TRUE, sep= ";", dec=",", na.strings=" ") #importa dataset "anova2_1R.csv" #Visualizzo un estratto del dataset head(data_frutti) > head(data_frutti) zona risposta varietà 1 6.9 1 1 11.8 1 1 6.2 1 1 9.2 1 1 9.2 1 1 6.2 1 #Uso il comando ‘colnames’ che permette di visualizzare il nome delle variabili colnames(data_frutti) > colnames(data_frutti) [1] "zona" "risposta" "varietà" #Utilizzo il comando ‘attach’ per gestire le variabili con il loro nome attach(data_frutti) #Comunico al software la natura nominale categorica delle variabili blocchi zona<-as.factor(zona) varietà<-as.factor(varietà) #Calcolo le statistiche di sintesi della variabile risposta, della variabile varietà e della variabile zona summary(risposta) > summary(risposta) Min. 1st Qu. Median Mean 3rd Qu. Max. 5.000 7.075 9.200 9.457 12.100 14.100 summary(varietà) > summary(varietà) 1 2 3 4 18 18 18 18 summary(zona) > summary(zona) 1 2 3 24 24 24 #Applico l’analisi della varianza (ANOVA) a 2 vie con interazione anova(lm(risposta~varietà+zona+varietà:zona)) > anova(lm(risposta~varietà+zona+varietà:zona)) Analysis of Variance Table Response: risposta Df Sum Sq Mean Sq F value Pr(>F) varietà 3 325.57 108.525 37.7431 7.828e-14 *** zona 2 31.51 15.753 5.4788 0.006525 ** varietà:zona 6 33.17 5.529 1.9228 0.091676 . Residuals 60 172.52 2.875 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Esercizio-esempio 2 La tavola seguente riporta dei punteggi sulla maturità emotiva di 27 giovani maschi classificati secondo l’età e secondo l’uso di marijuana. Valutare le differenze tra le medie per maturità emotiva secondo i fattori A( uso di marijuana), B (età) e l’interazione dei due A*B. Sia alfa = 0.05 per tutti i test. Fattore A ( uso di marijuana) Fattore B (Età) Mai Occasionalmente Giornalmente 25 18 17 15-19 28 23 24 22 19 19 28 16 18 20-24 32 24 22 30 20 20 25 14 10 25-29 35 16 8 30 15 12 Var risposta= punteggio maturità emotiva Var trattamento A = colonne –uso di marijuana Var trattamento B = righe- età Interazione =uso marijuana x età Unità sperimentali = singoli soggetti repliche per uso marijuana ed età H0 : α = α = … α = 0 gli effetti del trattamento A colonna sono uguali e nulli; α 1 2 i HA : non tutti gli α = 0 α i ------------------------------------------------- H0 : β = β …. β = 0 gli effetti del trattamento B riga sono uguali e nulli; β 1 2 j HA : non tutti gli β = 0 β j --------------------------------------------------- H0 : α β = α β …= α β = 0 gli effetti della interazione AB sono uguali e nulli; α β 1 1 1 2 ij HA : non tutti gli α β = 0 α β ij Numero trattamenti A colonne= k=3; numero trattamenti B righe = j =3 Numero ripetizioni per interazione trattamento A x trattamento B = n = 3 Gradi di libertà totali =(k*j*n)-1= (3*3*3) -1 = 27-1= 26 Gradi di libertà tra trattamenti A-colonne = k-1 = 3-1= 2 Gradi di libertà tra trattamenti B-righe = j-1 = 3-1 = 2 Gradi di libertà della interazione AB =( k-1) (j-1)= 2*2 =4 Gradi di libertà della variazione residua-errore =k*j*(n-1)= 3*3*(3-1)= 18 F critico per RV trattamento A: alfa= 0.05, 2 gdl al numeratore / 18 gdl al denominatore = 3.55 F critico per RV trattamento B: alfa= 0.05, 2 gdl al numeratore / 18 gdl al denominatore =3.55 F critico per RV interazione fattori AB colonne-righe: alfa= 0.05, 4 gdl al numeratore / 18 gdl denominatore = 2.93 Analisi varianza: a due fattori con replica RIEPILOGO 15-19 Conteggio 3 3 3 9 Somma 75 60 60 195 Media 25 20 20 21.66667 Varianza 9 7 13 13.5 20-24 Conteggio 3 3 3 9 Somma 90 60 60 210 Media 30 20 20 23.33333 Varianza 4 16 4 31 25-29 Conteggio 3 3 3 9 Somma 90 45 30 165 Media 30 15 10 18.33333 Varianza 25 1 4 88.75 Totale Conteggio 9 9 9 Somma 255 165 150 Media 28.33333 18.33333 16.66667 Varianza 15.75 12.25 30.25 ANALISI VARIANZA Origine della variazione SQ gdl MQ F Valore di significatività F crit Campione-righe-età 116.6667 2 58.33333 6.325301 0.008308 3.554561 Colonne-uso marijuana 716.6667 2 358.3333 38.85542 2.94E-07 3.554561 Interazione 183.3333 4 45.83333 4.96988 0.007071 2.927749 Errore residuo 166 18 9.222222 Totale 1182.667 26 Quindi rifiuto H0 rifiutoH0 rifiuto H0 Accetto le rispettive HA. α, β, α β. I risultati indicano che sia l’uso di marijuana sia l’età che l’interazione dei due fattori hanno un effetto significativo sulla maturità emotiva. In particolare in presenza di interazione significativa dei fattori, l’effetto dei singoli fattori viene subordinato a questa ultima, ovvero l’uso di marijuana per età. Degno di nota è il valore di F e relativa significatività per il trattamento A uso di marijuana che indicherebbe un effetto più forte per questo fattore. …… Se osserviamo le medie della tabella riportata notiamo che effettivamente chi non fa mai uso di marijuana nella età minore ha maturità emotiva più alta di chi fa uso giornaliero nella età maggiore…… ulteriori valutazioni si rendono opportune per queste interazioni…... Controlliamo anche con il programma STATA . anova varrisposta usomarijuana##et Number of obs = 27 R-squared = 0.8596 Root MSE = 3.03681 Adj R-squared = 0.7973 Source | Partial SS df MS F Prob > F ---------------+---------------------------------------------------- Model | 1016.66667 8 127.083333 13.78 0.0000 | usomariju~a | 716.666667 2 358.333333 38.86 0.0000 et | 116.666667 2 58.3333333 6.33 0.0083 usomariju~a#et | 183.333333 4 45.8333333 4.97 0.0071 | Residual | 166 18 9.22222222 ---------------+---------------------------------------------------- Total | 1182.66667 26 45.4871795 Il risultato è uguale Esercizio-esempio 3 Un esperimento in soggetti adolescenti è stato programmato per studiare gli effetti di tre farmaci diversi in tre tipi di condizioni da stress, che procuravano ansia. La tavola riporta le differenze tra i punteggi, pre – e post- trattamento dei 18 soggetti che hanno partecipato all’esperimento. Valutare se esistono differenze per livelli diversi dei due fattori e la loro interazione. Farmaco Condizioni (Fattore A) da stress (Fattore B) A B C I 4 1 1 5 3 0 II 6 6 6 6 6 3 III 5 7 4 4 4 5 Var risposta= effetto dei farmaci espresso in punteggio Var trattamento A = colonne –tipo di farmaco Var trattamento B = condizioni da stress Interazione =tipo farmaco x condizioni da stress Unità sperimentali = singoli adolescenti repliche per farmaco e condizioni da stress H0 : α = α = … α = 0 gli effetti del trattamento A colonna sono uguali e nulli; α 1 2 i HA : non tutti gli α = 0 α i ------------------------------------------------- H0 : β = β …. β = 0 gli effetti del trattamento B riga sono uguali e nulli; β 1 2 j HA : non tutti gli β = 0 β j --------------------------------------------------- H0 : α β = α β …= α β = 0 gli effetti della interazione AB sono uguali e nulli; α β 1 1 1 2 ij HA : non tutti gli α β = 0 α β ij Numero trattamenti A colonne= k=3; numero trattamenti B righe = j =3 Numero ripetizioni per interazione trattamento A x trattamento B = n = 2 Gradi di libertà totali =(k*j*n)-1= (3*3*2) -1 = 18-1= 17 Gradi di libertà tra trattamenti A -colonne = k-1 = 3-1= 2 Gradi di libertà tra trattamenti B -righe = j-1 = 3-1 = 2 Gradi di libertà della interazione AB =( k-1) (j-1)= 2*2 =4 Gradi di libertà della variazione residua-errore =k*j*(n-1)= 3*3*(2-1)= 9 F critico per RV trattamento A: alfa= 0.05, 2 gdl al numeratore / 9 gdl al denominatore = 4.26 F critico per RV trattamento B: alfa= 0.05, 2 gdl al numeratore / 9 gdl al denominatore =4.26 F critico per RV interazione fattori colonne-righe: alfa= 0.05, 4 gdl al numeratore / 9 gdl al denominatore = 3.63 Analisi varianza: a due fattori con replica RIEPILOGO A B C Totale Stress I Conteggio 2 2 2 6 Somma 9 4 1 14 Media 4.5 2 0.5 2.333333 Varianza 0.5 2 0.5 3.866667 Stress II Conteggio 2 2 2 6 Somma 12 12 9 33 Media 6 6 4.5 5.5 Varianza 0 0 4.5 1.5 Stress III Conteggio 2 2 2 6 Somma 9 11 9 29 Media 4.5 5.5 4.5 4.833333 Varianza 0.5 4.5 0.5 1.366667 Totale Conteggio 6 6 6 Somma 30 27 19 Media 5 4.5 3.166667 Varianza 0.8 5.1 5.366667 ANALISI VARIANZA Origine della variazione SQ gdl MQ F Valore di significatività F crit Campione-righe-stress 33.44444 2 16.72222 11.57692 0.003247 4.256492 Colonne-farmaco 10.77778 2 5.388889 3.730769 0.066065 4.256492 Interazione 9.888889 4 2.472222 1.711538 0.230886 3.63309 Residuo 13 9 1.444444 Totale 67.11111 17 Quindi rifiuto H0 rifiutoH0 non rifiuto H0 α, β, α β. Accetto le rispettive HA e HA H0 α β e α β. I risultati indicano che sia il tipo di farmaco che le condizioni da stress danno risultati significativamente sugli effetti del farmaco, ma non l’interazione dei due fattori. Lo stress inoltre appare avere un effetto più forte rispetto al tipo di farmaco sulla variabile risposta. Controlliamo anche con il programma STATA anova varrisposta stress##farmaco Number of obs = 18 R-squared = 0.8063 Root MSE = 1.20185 Adj R-squared = 0.6341 Source | Partial SS df MS F Prob > F ---------------+---------------------------------------------------- Model | 54.1111111 8 6.76388889 4.68 0.0166 | stress | 33.4444444 2 16.7222222 11.58 0.0032 farmaco | 10.7777778 2 5.38888889 3.73 0.0661 stress#farmaco | 9.88888889 4 2.47222222 1.71 0.2309 | Residual | 13 9 1.44444444 ---------------+---------------------------------------------------- Total | 67.1111111 17 3.94771242 Il risultato è uguale
Description: