Table Of Content

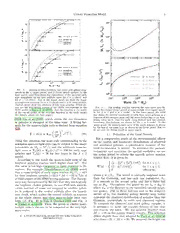
February2,2008: Not toappearin NonlearnedJ.,45. PreprinttypesetusingLATEXstyleemulateapjv.03/07/07 A SUBHALO-GALAXY CORRESPONDENCE MODEL OF GALAXY FORMATION Juhan Kim1,2, Changbom Park1,3, and Yun-Young Choi1,4 February 2, 2008: Not to appear inNonlearned J., 45. ABSTRACT We propose a model of allocating galaxies in cosmological N-body simulations. We identify each subhalo with a galaxy,and assign luminosity and morphologicaltype assuming that the galaxy lumi- nosityisamonotonicfunctionofitshostsubhalomass. Themorphologyassignmentismadebyusing two simple relations between subhalo mass and galaxy luminosity of different types. One is using a 8 constant ratio in luminosity of early (E/SO) and late (S/Irr) type galaxies at a fixed subhalo mass. 0 0 And the other assumes that galaxies of different morphologicaltypes but having an equal luminosity 2 have a constant ratio in their subhalo masses. We made a series of comparisons of the properties of these simulated galaxies with those of the SDSS galaxies. The resulting simulated galaxy sample n is found to successfully reproduce the observed local number density distribution except for in high a density regions. The luminosity function is studied as a function of local density. It was found that J the observed luminosity functions in different local density environments are overall well-reproduced 1 by the simulated galaxies. Discrepancy is found at the bright end of the luminosity function of early 2 types in the underdense regionsandatthe faintendof bothmorphologicaltypes in veryhighdensity regions. A significant fraction of the observed early type galaxies in voids seems to have undergone ] h a relatively recent star formation and became brighter. The lack of faint simulated galaxies in dense p regions may be due to the strong tidal force of the central halo which destroys less massive satellite - subhalos around in the simulation. The mass-to-lightratio is found to depend on the local density in o thewaysimilartothatobservedintheSDSSsample. Wehavefoundanimpressiveagreementbetween r t out simulated galaxies and the SDSS galaxies in the dependence of the central velocity dispersion on s a the local density and luminosity. [ Subject headings: Cosmology: simulation: halo-galaxy: luminosity function: Numerical 1 v 1. INTRODUCTION have reported successful recovery of observational fea- 9 tures of the galaxy distribution like the two-point cor- 6 The current galaxy formation paradigm can be char- relations of galaxies (Conroy et al. 2006; Kravtsovet al. 1 acterized by “hierarchical clustering”. This means that 2004; Berlind & Weinberg 2002), topology (Park et al. 3 massive dark matter halos form by merging less massive 2005a,b;Gott et al.2006),andtheenvironmentaldepen- . halosand/orby accretingambientmatter, andalsothat 1 dence of spin distributions (Cervantes-sodi et al. 2007). a dark matter halo governs the evolution of the galaxy 0 Detailedmodelingofgalaxyevolutionandunderstand- residing inside. Most galaxies are believed to be hosted 8 ing of the galaxy properties have been possible with 0 bythedarkmatterhalosbecuasethehaloscanprovidea the recent advent of the huge redshift surveys such as : deep potential well for baryonic matter to condense and v Sloan Digital Sky Survey5 (SDSS) and 2dFGRS6. These cooldown. Thisleadstotriggeringofthestarformation; i larger surveys provide a rich information on the for- X gas sufficiently accumulated in the halo potential cen- mation and evolution of galaxy. To meet a require- ter begins to experience many hydrodynamic processes, r menttoestablisharelationbetweensimulatedstructures a such as radiative cooling, star-formation, supernova ex- and observed galaxies many techniques have been intro- plosion,andchemicalenrichments. Alloftheseprocesses duced. The semi-analytic model(SAM) of galaxy for- play an important role in making the visible galaxies in mation (Cole et al. 1994; Kauffmann et al. 1997; Baugh the end. Because galaxies as a building block of the 2006) is based on the hierarchical clustering of halos large scale structures consequently follows the evolution whose merging history trees are built by generating a oftheirhosthalosoverthecosmichistory,understanding set of Gaussian random numbers. The mass growth his- gravitationalevolutionofdarkhalosisveryimportantfor toryofhalosonvariousmassscalescanbegeneratedand the study of galaxy formation and evolution. traced by this method. Numerous SAM parameters are Over the past few decades, cosmological simulations implementedinthe merginghistoryto reflectthe hydro- have been proved useful for the study of structure for- dynamical processes of heating, cooling, star formation, mation. Simulations have boosted up many investi- and aging the stellar populations. Their parameter val- gations of the nonlinear structure evolutions and their ues are fine tunned for the best description of collective results have been extensively compared to the obser- properties of observed galaxies. But as the number of vations in various aspects of interest. Many studies observationalcontraintsincreases,thenumberofparam- 1KoreaInstituteforAdvancedStudy,Hoegiro87,Dongdaemun- etersincreasesandtheSAMbecomesmuchcomplicated. Gu,Seoul,130-722, Korea Hydrosimulations employ direct formulations of the [email protected] [email protected] 5 http://www.sdss.org [email protected] 6 http://www.aao.gov.au/2df/ 2 Kim, Choi, and Park hydrodynamic processes (Weinberg et al. 2006). Two thestatisticalpropertiesofsimulatedgalaxieswiththose types of hydro simulations are now widely adopted; the ofgalaxiesobservedbytheSDSS.Weorganizethispaper Lagrangian (Monaghan 1992; Hernquist & Katz 1989) as follows. In section 2 we describe our simulation and andEulerianmethods(Tasker & Bryan2006;Harten, A. the subhalo finding method. In section 3, we implement 1997, and for comparative study, see Heitmann et al. the subhalo-galaxycorrespondencemodel andshow how 2005; Thacker et al. 2000). They set gas particles or gas to assign morphological types to mock galaxies. In sec- grids in the system of interest. Then, gas dynamics are tion 4, the local density is introduced to quantify local taken into account by calculating the hydrodynamic in- environmentsandthelocaldensitydistributionsofmock teractions between neighbor particles or by solving dif- andSDSSgalaxiesareinvestigated. Wealsocomparethe ferential hydro equations between adjacent grids. This luminosity distribution of simulated galaxies with those methodhasseveralweakpoints;itsuffersfromthelackof of the SDSS galaxies in section 5. The environmental resolutionsinspaceandmassastheN-bodysimulations. dependence of central velocity distributions are studied Andinmostcases,thestarformationandsupernovaex- for the mock and SDSS galaxies in section 6. And dis- plosions are far beyond the simulation resolution. Some cussions and conclusions follow in section 7. processes such as radiative transfer, star formation, su- pernovae feedback, and initial stellar mass function, are 2. SIMULATIONANDHALOFINDING not thoroughly understood and are difficult to parame- We have carried out a cosmological N-body simula- terize in a well established way. tion of the universe with the WMAP 3-year cosmolog- One of the offsprings of the SAM is the Halo Oc- ical parameters. We ran 10243 cold dark matter par- cupation Distribution (HOD; Zheng et al. 2005; Seljak ticles using an improved version of the GOTPM code 2000; Berlind & Weinberg 2002) model. It relates the (Dubinski et al. 2004). The code adopts a dynamical Friend-of-Friend (FoF) halo mass to the number of con- domaindecompositionfor the Particle-Meshpartwith a tained subhalos (or galaxies) using a conditional proba- variable width of the z-directional domain slabs. It also bility, P(N M), where M is the FoF halo mass and N usesmorecompactandefficientoct-siblingtreewalksre- | is the number of subhalos inside the FoF halo. This ducing the computational cost for the short-range force probability function is obtained from numerical simu- update which consumes about 90 % of total run time. lations (Kravtsov et al. 2004; Berlind & Weinberg 2002; As a results, this new version outperforms the previous Jing et al. 1998) or from observations (Zehavi et al. version by about factor three in speed. The simulation 2004; Abazajian et al. 2005; Zheng et al. 2007) fitting was run on a beowulf-type system installed at KoreaIn- the model to the observed two-point correlation func- stitute forAdvancedStudy. Thelinuxclusterconsistsof tions. 256 AMD cores and 1 tera-byte main memory. Another variant of the SAM is a one that The simulation and cosmological parameters adopted adopts the one-to-one monotonic correspondence be- in this study are lists in Table 1. The number of time tween the galaxy luminosity and subhalo mass steps in the simulations are empirically pre-determined (Marinoni & Hudson 2002; Vale & Ostriker 2004, 2006; to satisfy the requirement that the maximum displace- Shankar et al. 2006). This method is often called the ment of particles in a step should be less than the force “correspondence model”. It is simpler than other meth- resolutionswhichis0.1timesthemeaninterparticlesep- ods because it requires only two prerequisites; the lumi- aration (d ). The starting epochs of simulations are mean nosityfunctionofgalaxiesandmassfunctionofsubhalos. chosen to constrain that any particle should not over- Its key assumption that a more massive subhalo hosts a shoot neighbors when the Zel’dovich displacement is brighter galaxy, is consistent with the hierarchical clus- made. tering picture. As the halo mass grows, its luminosity Subhalos are identified by the PSB method is expected to grow in general because merging of halos (Kim & Park 2006). The method applies the FoF may be followed by the merging of galaxies. By match- algorithmto identify dark matter particle groups adopt- ing these two functions, the subhalo mass is mapped to ingthestandardlinkinglength,l =0.2d . Thenit link mean galaxy luminosity. divideseachFoFhalointosubhalos. Thistwo-stagehalo However, sometimes a galaxy may survive the merger findingisincommonwithothermethods(Springel et al. eventbecause baryoniccomponentof a galaxyis usually 2001; Shaw et al. 2006). In the second stage we build more concentrated and is more tightly bound than its a particle density field by a coordinate-free method as dark counterpart. These “orphan” galaxies (Gao et al. usuallyadoptedinthesmoothedparticlehydrodynamics 2004) which have no separate corresponding halos could (Monaghan 1992). This adaptive kernel implementation exist in the cluster regions. Also halos of mass below a isintendedtoresolvetightclusteringsofparticles. Then, certaincharacteristicscaleareunabletoprovidebaryonic we search for 26 nearest neighbors at each particle. To matterwithgravitationalattractionstrongenoughtore- constructisodensitycontourwemovealongtheneighbor sist against supernova explosions which can tear up the positions in a similar way used in the origingal PSB small-mass system. Even though such cases are many, method (for details see Kim & Park 2006). Self-bound it is sound to expect that the galaxy census is closely and tidally stable subhalos are identified by measuring related to the population of subhalos because most of the tidal radius of the subhalos and total energies of the observed galaxies are field galaxies who have their their member particles; member candidates are selected own dark halos. It is worth investigating the hypothesis if their distances to the center of a subhalo are less ofthesubhalo-to-galaxycorrespondencemodelofgalaxy than tidal radius of the subhalo. Among these particles, formation. gravitationally unbound particles are discarded. The In this paper, we apply the subhalo-galaxy correspon- resulting subhalos are used to allocate galaxies. We dence model to a large N-body simulation and compare call the most massive subhalo a central halo and other Galaxy Formation Model 3 subhalos satellite halos in the FoF group. Also, the where we adopt the type-specific Schechter function pa- group of particles found by the FoF method are named rameters ⋆ 5log h = 20.23, φ⋆ = 7.11 the FoF group or FoF halo. 10−3h3MpMc−E3, −and α10= 0.5−3 for earlEy type galax×- E 3. THESUBHALO-GALAXYCORRESPONDECEMODEL i1e0s−3ahn3dMpMc−⋆L3,−an5dlogα10h==−0−.9200.f1o2r,laφt⋆Le ty=pes12i.n27th×e We use the monotonic one-to-one correspondence L − r band, which are given in Table 2 of Choi et al. (2007) model between galaxies and subhalos; there is one and for the SDSS galaxies brighter than = 19.0 (Here- onlyonegalaxyineachsubhaloandamoremassivesub- Mr − after, we will drop the term 5log h in the absolute halohostsamoreluminousgalaxy. Weapplythismodel 10 magnitude and the magnitudes are all r–band magni- to assign galaxies within our simulation box. tude.) These parameter values are quite different from The one-to-one correspondence model is formalized in those given by Blanton et al. (2001) and Blanton et al. the following way. We first measure the mass function (2003) mostly because we are using the type-specific Φ(M ) of PSB subhalos. We then take the observed h functions. Reducing the effects of the internal extinc- luminosity functions of the early(E/S0)andlate (S/Irr) tion by Choi et al. also makes a significant difference type galaxies. The relation between the halo mass and in the α parameter compared to Blanton et al.’s results. the corresponding absolute magnitude limits is given by Difference also comesfromthe data size (Dr4plus versus the following integral equation. DR1), adopted cosmology (Ω = 0.27,Ω = 0.73 ver- m Λ ∞ ME(Mh) ∼susΩ =0.3,Ω =0.7),andsampledefinition(volume- Φ(M′)dM′= φE( ′)d ′ limitemd versus aΛpparent magnitude-limited). ZMh Z−∞ M M The β model can be easily solved by using the rela- ML(Mh) tion, (M )= (M ) 2.5log β in equation (1), +Z−∞ φL(M′)dM′, (1) but thMe Lκ mohdel iMs aEbit thric−ky to so1l0ve and needs a few assumptions. The κ model can be solved by a chain of whereΦisthesubhalomassfunctionandφ andφ are E L equations whose n–th term is, the luminosity functions of early and late type galaxies. In this equationwe separate the full luminosity function Mh Mn−1 Φ(M)dM= φ ( )d oafccsouubnhtaltohseindtiofftehreonseceofineamrlyasasndoflattheetyhpaelosstoastsaokceiaintetdo ZMh/κ ZMn−2 L M M with galaxies of different morphologicaltype. Mn + φ ( )d , (5) Two models are proposed to utilize the simple mass ZMn−1 E M M and luminosity scaling ratios between different morphological types at the fixed luminosity and at the fixed where n−2 n−1 n and M ≤M ≤M mass, respectively. The first model uses Mh( L,n−2)=Mh( E,n−1) m (6) M M ≡ LL(Mh)=LE(κMh), (2) Mh( L,n−1)=Mh( E,n)=m/κ, (7) M M where Mh is the subhalo mass, and LL and LE are the for κ>1. Here Mh( L) and Mh( E) denote the halo luminosities of late and early types, respectively. The masses of late type Mand early typeMgalaxies of absolute equation means that at an equal luminosity the early magnitude , respectively. If Mh, n−2, and n−1 type galaxy is κ times more massive than the late type aregiven,thMen canbe derived. FMigure 1 depicMts the n galaxy. This model is based on the findings of Park et M relations among the three magnitudes described above. al. (2007a)whohaveassuredthattheearlytypegalaxies The solid and dashed curves show the luminosity func- brighter than Mr = 19.5 have about √2 times higher tions of early and late types, respectively. And the dot- − centralvelocitydispersionandpairwisepeculiarvelocity tedlineconnectsthesamemassofthetwomorphological differencecomparedtothelatetypesofthe samebright- types. The shaded areas denoted by A and B are the n n ness. This implies κ 2 if (Mh/L)E = κ(Mh/L)L. An- integratednumberdensitiesofgalaxiesofmagnitudebe- ≈ otherconvencingobservationalevidenceforκ=2canbe tween n−2 and n−1 for the late type and between alsofoundinMandelbaum et al.(2006)whoobtainedthe n−1Mand n forMthe early type, respectively. There- same result for halos of mass greater than 1011h−1M⊙ fMore,the sumMof the twoshadedareasshouldbe equalto from the analysis of the galaxy-galaxy weak lensing of the integralsof the subhalo mass function (the left-hand the SDSSsample. Equation(2)thenmakesequation(1) side of Eq. 5). By making a stride to the next mass aone-to-onerelationbetweenhalomassandgalaxylumi- scale which is smaller by 1/κ times, we can get a chain nosity. From now on, we name it κ model. The second of equations and derive the scaling relation between the model uses a constant factor for the luminosity rather massandtheluminosity. Tosolvethischainofequations than the mass. This relation can be formulated as we set initial conditions under the plausible assumption that the late-type contributions to the number density L (M )=βL (M ), (3) L h E h atthe high-mass(orbright)endarenegligiblecompared whichsaysthatlatetypegalaxiesarebrighterthanearly to those of early types (or 0 A ,A B ,B ). This 1 2 1 2 type galaxiesof the same massby a factorof β. Now we ≃ ≪ settingisquitefairfromthefactthatearlytypegalaxies call it the β model. dominate the bright end population of galaxies. Then, For the galaxy luminosity distribution, we use the we are able to solve the series of equation (5) from the Schechter function initial conditions where only the early-type contribution φ( )=(0.4ln10)φ⋆10−0.4(M−M⋆)(α+1) to number density is dominant. M Now we investigate the early type fractions as a func- exp 10−0.4(M−M⋆) , (4) tion of the host subhalo mass. The probability of a h− i 4 Kim, Choi, and Park TABLE 1 Simulationparameters name Np Nm Lboxa Nstep zi h Ωm Ωb ΩΛ nsb b mpc ǫd H2 10243 10243 256 3800 95 0.732 0.238 0.042 0.762 0.958 1.314 1.0×109 25h−1kpc a inh−1Mpc b spectralpowerindex c particlemassinh−1M⊙ d forceresolution Fig. 1.— Illustration to derivethe Mh–Mr relation forthe κ. The solidand dashed curves are the luminosityfunctions of early andlate type galaxies, respectively. Andthe dotted lineconnects Fig. 2.— Early type fractions as a function of host subhalo the same mass of the two types. The shaded areas tagged by An mass. Each curve shows the fractional distributions of early type baannetddwMeBennnMaforernt−thh2eeaennaudrlmyMbteynrps−e1,ofrfeogsraptleahcxetiievlsaetlyien.tythpee amnadgnbiettuwdeeeninMternva−l1s g2aa,ttlaaancxhdieesd3fto(ourptβphee=rcp1ua,rnv1ee.5sl)., m2,oadnedls.3T(lohweemropdaenlelp)aaranmdeftoerrκva=lu1e,s1a.r5e, galaxy of mass Mh to be early type is given by Mh–M relation for the early type galaxies with β = 2, and κ=2 and 3. φ ( M ) E E h In the lower panel of Figure 4 shows the mass versus f (M )= M | , (8) E h φ ( M )+φ ( M ) luminosityrelation(solidline)fortheearlytypegalaxies. E E h L L h M | M | where the denominator is the luminosity function of all HereweadoptM⊙ =4.64−5log10h(Blanton & Roweis 2006)totransformthemagnitudetoluminosityinther– galaxiesofmassM andthenumeratoristheluminosity h bandfilter. Itcanbenotedthatgalaxyluminositydrops function of early types of mass M . Figure 2 shows the h steeply at the low mass end and rises in a power law at results for the κ and β models. Using f we are able to E the high mass end. Taking into account these features, randomlyassignmorphologicaltypetoeachmockgalaxy we propose a function inaccordancewithitshalomass. Foralargervalueofβ, tdhoewenatrolylotwypeer mgaalsasxysctaelensds(Mto)daonmdinbaetleowthMe pofpuldartoiopns L(M)= M⋆ M⋆ γ−1e−(MM⋆), (9) c c E Ψ (cid:18) M (cid:19) more rapidly. But for the κ model, those changes in f ml E are not so much steep. Also, in this plot, we note that a as a fitting function for the halo mass versus early-type moredramaticchangeofthe f inthe β modelthanthe galaxy luminosity relation. We apply the χ–square fit- E κ model. tingtotherelationandobtainthebest-fitparameterval- Figure 3 shows the relation between the subhalo mass ues of Ψml = 38.3hM⊙/L⊙, M⋆ = 2.04 1011h−1M⊙, × M andabsolutemagnitude ofearly(solid lines)and and γ = 0.644 for the early type in the β = 2 model. h late (dashed lines) type galaMxies derived from equation In the κ = 2 model, Ψml = 39.8(20.3)hM⊙/L⊙, M⋆ = (1) and the luminosity functions of the SDSS galaxiesin 4.83(1.52) 1011h−1M⊙, and γ =0.667(0.719)for early × the κ (upper) and β (lower panels) models. Only shown (late) type. Only the fitting result for the early type arethecasesofβ =2(thicklines)and1.5(thinlines)and in the β = 2 model is shown by a short-dashed line. κ=2 (thick lines) and 3 (thin lines). For a comparison, Thetoppanelshowsthe mass-to-lightratiosofthe early the characteristicminimum mass of the centralsubhalos (solidcurve)types in the β =2 model. The long-dashed at each absolute magnitude limit estimated by Zheng and dotted curves show those ratios of early and late et al. (2007) based on the HOD model is given as filled type galaxies in the κ = 2 model. In the β = 2 model, circles. Theyobtainedthemagnitude-to-massrelationof thereisaupturnofthe mass-to-lightratioofearlytypes the central subhalo but ignored the morphologicaltypes around Mu = 3 1011h−1M⊙ (for those measured in × ofgalaxies. The HODmodelisquite consistentwithour other bands, see van den Bosch et al. 2003; Yang et al. Galaxy Formation Model 5 -22 -21 -20 -19 -22 -21 -20 -19 Fig. 3.— Scaling relation between halo mass and galaxy magnitude inthe κ (upper panel) and β (lower panel) models. In the lowerpanel,solidlinesshowsthedependenceofthemodeledearly type magnitude on the host subhalo mass for β = 2 (thick) and for β = 1.5 (thin). And in the upper panel, we show the mass- to-magnitude relations forκ=2(thick) andκ=3(thin) models. Dashed curves show the relations of late type galaxies. Filledcir- cles are the best-fitting results of the SDSS observations to the Fig. 4.— The scaling relation between the halo mass and the HODmodelinZhengetal.(2007). Andtheerrorbaristhewidth galaxyluminosity(lowerpanel)ormass-to-lightratio(upperpanel) of the cut-off profile of the step-like function in the HOD model in the β = 2 and κ = 2 model. In the lower panel, the solid (fordetails,pleaseseetheirpaper). lineshowsthederivedluminosityofearlytypemockgalaxiesasa functionofthesubhalomassandtheshortdashedlineisthebest- 2003; Eke et al. 2006), which means the star formation fitting curve for it. Alsothe early (long dashed) and late (dotted) in galaxies is strongest at the mass scale. A fitting for- luminosity distributions are shown for the κ = 2 model. In the mula for the mass-to-lightratiois derivedfromequation upperpanel,themass-to-lightratioofthemockgalaxiesisshown bythe lineof the sametype as showninthe lowerpanel. Butwe (10), donotplotthefittingresultinupperpanel. γ M (M⋆) Υ M/L=Ψ e M . (10) 4.1. Definition of the Local Density ≡ ml(cid:18)M⋆(cid:19) For a comparative study of the environmental effects Using this equation,the massscale correspondingto the on the spatial and luminosity distributions of observed minimummass-to-lightratiocanbe relatedtothe shape and simulated galaxies, a quantitative measure of the parameters as M = M⋆/γ and the minimum mass-to- u local environment is needed. To minimize the parame- light ratio is Υ (E) = Ψ (e/γ)γ 100 for early type u ml terizations and maximize the spatial resolution we use ≃ galaxies and Υ (L) 50 for late types in the β = 2 u the spline kernel to obtain the smooth galaxy number ≃ model. density field. It is given by According to our result the mass-to-light ratio of the brightest galaxies reaches much higher than 103. But 1 3q2+ 3q3 /(πh3) for 0<q 1, − 2 4 s ≤ this value is too high compared to those reported in lit- W(q)= ((cid:0)2 q)3/(4πh3(cid:1)) for 1<q 2, erature. For example, Mandelbaum et al. (2006) noted  0 − s otherwise≤, that a mass-to-lightof earlytypes reaches M /L =674 fortheirbrightestsamples( 22.5 2h2inrTab. 4 where q r/hs. The kernel is centrally weighted more oftheirpaper)oftheSDSSl−ensing≤gaMlaxi≤es−. Thediscrep- than the≡Gaussian, and has only one parameter, hs. ancymaybeexplainedbythefactthattheyaretypically It is smooth to the second order and has a finite tail the brightest cluster galaxies. In our PSB halo identifi- out to 2hs. Throughout this paper we set hs = d20/2, cation method all mass not assigned to satellite galax- where d20 is the distance to the twentieth nearestneigh- ies is assigned to the central subhalo after the bound- bor galaxy. Due to these features and to the adaptive ness check, which makes the central subhalo as massive nature of hs the resulting galaxy density map better as the whole cluster and their mass-to-light ratio very represent the observed distribution of galaxies than the large (cf. Fig. 10 in Vale & Ostriker 2006 and Fig. 4 Gaussian, particularly in voids and clustered regions. in Tinker et al. 2005). Then, the group or cluster mass- To compare the observed and mock galaxy samples, it to-light ratio is the one to be comparedat the very high is necessary to make the number density of the den- mass scales. sity tracers the same. We use galaxies brighter than = 20 as the galaxy density tracers. This selection 4. ENVIRONMENTALEFFECTSONTHEGALAXY Mdiffers−slightly from that adopted by Park et al. (2007a) DISTRIBUTION who chose 21< < 20. We removedthe brightcut − M − 6 Kim, Choi, and Park to better resolve the centers of clusters where galaxies brighter than L are concentrated. ⋆ 4.2. Number Density Distributions Thelocaldensityatgalaxypositionsismeasuredinour SDSS volume-limited samples. The density estimate is correctedfortheboundaryeffectswhenthekernelsphere of radius d overlaps with the survey boundary. The 20 late type galaxies having axis ratio b/a < 0.6 are re- moved from the sample to reduce the effects of internal absorption on luminosity. After this exclusion, we give the weight of 1/0.505 to late type galaxies to correct the galaxynumber density for the missing inclined ones, where 0.505 is the fraction of late types with b/a > 0.6 inasamplecontaininggalaxiesdownto = 17.5(the M − CM sample of Choi et al. 2007). The correction for boundary effect is unnecessary for mock galaxies since their distribution is periodic in all directions. The redshift distortions effects causedby the peculiar velocities are mimicked by shifting the mock galaxies along the x axis using x′ = x+v /H , where x 0 v is the x-component of peculiar velocity and H is the x 0 hubble constant. Figure 5 shows the distribution of local density (open circles) at the locationof galaxiesin two volume-limited SDSS samples with absolute magnitude limits of 20.0 − (D5) and 18.5 (D2) for the β =2 model. Also plotted − are the local density distributions of simulated galaxies selected by the same magnitude-limit criteria. It can be noted that the local density distributions of the SDSS galaxies and the corresponding mock galaxies match closely to each other at all densities except for at high densities. Also those distributions for the κ = 2 model are shown in Figure 6 with the same criteria. Fig. 5.— Distributions of local overdensities for the sample Ostriker et al. (2003) employed a log normal function of mock (filled circles) and SDSS galaxies (open circles) in the magnitude ranges of M < −20 (upper) and M < −18.5 (lower to fit the one-point distribution of dark matter den- panels)intheβ=2model. Thedashedlineshowsthelog-normal sity and luminosity density in their hydro-simulation. A fittoobservations. spherical top-hat filter of constant radius is adopted in their study. They found a good agreement between the simulateddensitydistributionsandthelognormaldistri- TABLE 2 butionwhilethedistributionofluminositydensityshows Thelog normalfunctionparametersof thelocaldensity distributions of the a poor fit. We check how well the galaxy density distri- SDSSgalaxies bution,insteadofdarkmatterorluminosity,isdescribed by the non-normalized log normal function Mmin sample A(h−1Mpc)−3 µ σ Ξ(∆) dN(∆) = A e−(ln∆−µ)2/2σ2, (11) −18.5 D2 4.53×10−2 0.662 1.27 ≡ dlog ∆ √2πσ −20 D5 1.47×10−2 0.949 1.34 10 −20.5 D5 7.44×10−3 1.11 1.30 where ∆ ρ/ρ¯ and A is the amplitude of the distri- −21 D5 2.76×10−3 1.23 1.26 ≡ bution. The mean number density of galaxies is n = Alog e. Thebest-fitting resultsareshownwithdashed 10 lines in each panel of Figure 5 and the fitting param- densities (ρ/ρ¯<10) even though there is only one input eter values for various magnitude-limit ( ) samples parameter in our model. Late type galaxies dominate lim are listed in Table 2. As can be noted, Mbrighter galax- these regions. From these figures, it appears that the ies tend to be located at higher local densities. Also the galaxy morphology depends only on the halo mass and local density distribution becomes broader for brighter does not directly depend on environment. But the num- subsamplesif viewedinthe linearscale ofoverdensityor berdensityanalysisaloneisnotsosufficienttodrawany has nearly a constant width ( σ 1.29) in log-scale. definite conclusion of the environmental effect. We will Figure 7 and 8 shows the dhistiri≃bution of local density further investigate this effect by comparingthe luminos- atlocationsof early(circles)andlate (stars)type galax- ityfunctionsoftheSDSSwiththoseofthemockgalaxies ies in the β = 2 and κ = 2 models, respectively. Open in various environments in the next section. In the high symbols are for the SDSS samples and the rest are for density regions our model gives too few galaxies, which the simulated galaxies. The local density distributions isprobablydue tothe insufficientresolutionofthesimu- of the simulated early and late type galaxies are very lation to maintain small subhalos within clusters and to well matched with observations at low and intermediate the lack of gas physics. Galaxy Formation Model 7 Fig. 7.— Local overdensity distributions for the two morpho- Fig. 6.— SimilartoFig. 5butfortheκ=2model. logical types inthe β =2 model. The distributions of local overdensity of mock and SDSS galaxies (D5 and D2) are shown for two magnitude-limit samples M < −20 (upper) and M < −18.5 5. LUMINOSITYFUNCTION (lower panels). Open cirlces and open stars mark the distribu- tionsofoverdensityoftheearlytypeandlatetypeSDSSgalaxies. There have been several works reporting the environ- Andfilled circlesand skeletal starsarethose of mock galaxies for mental dependence of the galaxy luminosity function the corresponding types. We tag each panel with the magnitude (Parketal. 1994and2007ainobservationsandMo et al. criteriaofthesampleintheupper-leftcorner. 2004 in the HOD model). It was found that the char- acteristic galaxy luminosity (L⋆) is an increasing func- and for different morphological types. For this compar- tion of the local density, and the faint-end slope (α) of ison we use the luminosity functions measured from the theluminosityfunctionisinsensitivetothelocaldensity. D3 sample of Park et al. (2007a) because this absolute However,Parketal. (2007a)usedasplinekernelweight- magnitude-limited sample covers both bright and faint ingtoestimatelocaldensities,andMo et al.(2004)(also magnitudes well, relative to other volume-limited sam- Cooray 2005) use a spherical top-hat filter of a constant ples. The fitting of the measured luminosity functions radius. For a quantitative comparison between observa- to the Schechter formula is carried out by using the MI- tions and models the same density estimation scheme is NUIT 7 packageswhichemploy the maximumlikelihood required. method. In the previous section, we studied the one-point dis- Figure 9 and 10 show the comparison of the luminos- tributionofthelocaldensityatgalaxylocationsforeach ity functions in four differentlocaldensity regionsin the morphology sample of galaxies brighter than a certain β =2andκ=2 models. The resultingenvironmentand absolute magnitude limit. In this section, we investigate morphology-specific luminosity function reproduces the the distribution of the absolute magnitude of early and observations surprisingly well. However, there are no- late type galaxies located in different local density en- tabledisagreementsfortwocases. Atveryhighdensities vironment. This gives us environment and morphology- (ρ/ρ¯>10)theabundanceoffaintearlytypegalaxiesare specific luminosity function of galaxies. In our galaxy significantly low in the simulation. This is again proba- morphologyassignmentschemeweonlyusetheobserved blyduetothelackofsmallsubhalosthatweredestroyed total luminosity function and the parameter β (or κ), in high density environment. Another problem is seen the ratio of luminosity (or mass) of the early and late at low densities (ρ/ρ¯< 1), where the early type galax- types at a fixed mass (or luminosity). It will be inter- ies are too few in the bright end of luminosity function. esting to see how accurately our model reproduces the observedluminosity functions at different local densities 7http://wwwasdoc.web.cern.ch/wwwasdoc/minuit/minmain.html 8 Kim, Choi, and Park Fig. 9.— Luminosity functions of mock (curves) and SDSS (symbols) galaxies inthe β =2model. Each lineshows the luminosity functions of the mock galaxies; solid lines for total, dotted linesfor early type galaxies, and dashed lines forlate type galaxies. Forcomparison,weshowtheluminositydensitiesoftheSDSS subsamplesdividedbythesamedensitycuts. Thesampleselection criteriaarebasedonthe logscaleoflocaldensityandarewritten inthelower-rightcornerofeachpanel. Fig. 8.— SameasFig. 7butfortheκ=2model. It seems that the morphology transformatin to bright early types in underdense regions through close interac- tions and mergers is more efficient in the nature than in our model (Park et al. 2008 for observational evidence). In the high density regions, the κ = 2 model describes thenumberdistributionoffaintlatetypegalaxiesbetter than the β = 2 model while this κ model shows a slight overestimation in the population of faint late types in the mean fields (0.4 < log(ρ/ρ¯) < 1) compared to the observation. Figure 11 and 12 compare the parameter of the Fig. 10.— SimilartoFig. 9butfortheκ=2model. Schechter function best fit to the SDSS data (open symbols) and simulated galaxy samples (filled symbols) as a caldensityforearlytypegalaxiesinfoursubsampleswith function of local density in the β =2 and κ=2 models. absolute magnitude limits of 19.0> > 19.3 (bot- − M − The dependence of both r∗ and α on local density is tom curve). 19.3> > 20.1, 20.1> > 20.5, M − M − − M − qualitatively well-reproduced by the simulation. How- and < 20.5 (top curve with filled circles). The M − ever,thecharacteristicmagnitudeM∗ oftheearlytypes curves delineate the median value of σv in each local is significantlyfainteratρ/ρ¯<2 inthe simulation. This density bin, which monotonically increases as luminos- isduetopaucityofbrightearlytypegalaxiesinlowden- ity increases. We also plot the scaled one-dimensional sityregions,whichismentionedabove. Theparameterα velocity dispersion of the early type mock galaxies with of the simulation is quite different from the observation black symbols. Because the observedvelocity dispersion at ρ/ρ¯> 2 for early type galaxies. This is again due to is obtained by sampling the inner part ( 1′′.5) of the ≤ the flat faint end slope of the luminosity function of the galaxy, we have to apply a scaling factor to the mock simulated early type galaxies. galaxy velocity dispersions. Because it is irrelevant in this paper to derive the exact value of the scaling factor 6. CENTRALVELOCITYDISPERSION and apply it to the related analysis, we make a rough Figure13showsthecentralvelocitydispersionofearly estimation of the relation between σ and V , where los v type galaxies in the D3 sample. The gray symbols with σ is the line-of-sight aperture velocity dispersion and los connecting lines are the relationsbetweenσ andthe lo- V is the virial velocity. According to Lokas & Mamon v v Galaxy Formation Model 9 Fig. 11.— Dependence oftheSchechter parameter values, M⋆ Fig. 12.— SimilartoFig. 11butforκ=2model (top) and α(bottom panel), on the local density forthe SDSS D3 (open symbols) and Mock (filled symbols) samples in the β = 2 model. Circles mark the fitting values of full galaxy samples and boxesarefortheearlytypesamples. Openstarsandfilledhexagons areforthelatetypesoftheSDSSandmocksamples,respectively. In this plotwe add the errorbars onlyto the SDSS fitting values andconnect onlythemockresultswithsolidlinesforclarity. (2001), the resulting scaling ratio of the velocity dispersions, f ( σ /V ), is c los v ≡ 0.5.f .3 (12) c for the acceptable ranges of the velocity anisotropy and the concentration parameter in 0 < (r /R ) < 1, where a v r isthecomovingapertureradius. Hereweassumethat a V = σ , where σ is the three-dimensional velocity dis- v v v persionandV 2GM /R . Intherangeoff written v v v c ≡ in equation (12),pwe simply set fc = 0.8 ( < 20.5), M − f = 1 ( 20.5 < < 20.1), f = 1.1 ( 20.1 < < c c − M − − M 19.3), and f = 1.2 ( 19.3 < < 19.0) to match c − − M − for the mean amplitudes of velocity dispersions for each mock and SDSS sample pair. At a fixed luminosity the velocity dispersion of the early type mock galaxies increases as the local density increases for bright galaxies Fig. 13.— Mediandistributionofcentralvelocitydispersionsof SDSS(graysymbols)galaxiesandscaledone-dimensionalvelocity and the slopes are decreasing for the faint sample. It dispersionsof Mock(black symbols)galaxiesof earlytypes inthe is reassuring that this trend is exactly the kind of phe- fourmagnitude-limitsamplesdividedbyfourmagnitudecuts. The nomenonfoundintheobservation(gray symbols). While magnitude ranges of the subsamples are M < −20.5, −20.5 < M< −20.1, −20.1 < M < −19.3, and −19.3 < M< −19 from theswitchoftheslopeinthefaintestSDSSsamplesisnot toptobottom lines,respectively. clearly observed in the mock sample (it shows a nearly flat slope on the local environments), the change of the slope is similar to each other. Both observation and our 7. SUMMARY&CONCLUSION modelshowthatthemass-to-lightratiooftheearlytype We have proposed a model to assign galaxy luminos- galaxies is a function of environment, and that this de- ity and morphology to the dark subhalos directly iden- pendence in turn is a function of luminosity. The mass- tified in cosmologicalN-body simulations. It is assumed to-light ratio of the early types decreases as the local thatthe galaxyluminosity is a monotonicfunction ofits density increases for galaxies brighter than about ∗, host halo mass. In the κ model we assume that the halo M but increases for those fainter than about ∗+1. masses of early and late type galaxies of equal luminos- M 10 Kim, Choi, and Park ity have a constant ratio. Another alternative model is ple analyzed. the β model which assumes the constant luminosity ra- We have found an impressive agreement between our tio between equal-mass galaxies of different types. This simulated galaxies and the SDSS galaxies in the depen- model has been proposed by Marinoni & Hudson (2002) dence ofthe centralvelocity dispersiononthe localden- who found that the observed B–band luminosity func- sityandluminosity. Theearlytypegalaxiestendtohave tion of galaxies can be reproduced from the PS function higherσ orhighermassinhighdensityregionsatagiven v assuming double power-law mass-to-light ratios and de- luminosity when they are brighter than about ∗. In M rivedhalooccupationnumbers. Ithasbeenexpandedby other words, these bright galaxies tend to become rel- Vale & Ostriker (2004, 2006) who adopted the satellite atively fainter in high density regions at a given halo halomassfunctionsanddirectlylink subhalostothe ob- mass. This interesting dependence of the mass-to-light servedgalaxies. Inthispaper,wehaveintroducedthera- ratioonenvironmentwassuccessfullyreproducedbyour tioofluminosityoftheearlyandlatemorphologicaltype subhalo-galaxy correspondence model of galaxy forma- galaxies at a given halo mass, and derived type-specific tion. A more detailed study of this phenomenon will be mass-to-lightratios as a function of subhalo mass. They presented in a forthcoming paper. are used to assign luminosity and morphology to subhalos. The mass-to-light ratio of the early type galaxies derivedin this wayhas a minimum value ofΥ 100at u the scale of Mu 3 1011h−1M⊙ in the β = 2≃model. CBP acknowledges the support of the Korea Science ≃ × Themass-to-lightratiostartstoexponentionalyincrease and Engineering Foundation (KOSEF) through the As- below M and increases in a power law above M . trophysical Research Center for the Structure and Evo- u u Weusethelarge-scalebackgroundgalaxynumberden- lution of the Cosmos (ARCSEC). Funding for the SDSS sity as an environmentalparameter. The smooth galaxy and SDSS-II has been provided by the Alfred P. Sloan densityfieldisobtainedbyusingtheadaptivesplineker- Foundation, the Participating Institutions, the National nelwhichenabledustoresolvecrowdedregionswell. The Science Foundation, the U.S. Department of Energy, localdensitydistributionoftheSDSSgalaxiesiswellde- theNationalAeronauticsandSpaceAdministration,the scribed by the log normal function. The obtained log JapaneseMonbukagakusho,theMaxPlanckSociety,and normal parameter values indicate that brighter galaxies theHigherEducationFundingCouncilforEngland. The tend to locate in dense regions. The local density distri- SDSS Web Site is http://www.sdss.org/. butionofthesimulatedgalaxiesisquitesimilartothatof The SDSS is managed by the Astrophysical Research theSDSSgalaixesinvoidsandmoderate-densityregions Consortium for the Participating Institutions. The Par- for both morphological types. The underestimation of ticipatingInstitutionsaretheAmericanMuseumofNat- galaxypopulationin clustersis thoughtto be due to the ural History, Astrophysical Institute Potsdam, Univer- evaporation of subhalos by the dynamical friction and sity of Basel, Cambridge University, Case Western Re- tidal stripping. This can also explain the discrepance in serve University, University of Chicago, Drexel Univer- theluminosityfunctionoftheearlytypegalaxiesinhigh sity, Fermilab, the Institute for Advanced Study, the density regions. Japan Participation Group, Johns Hopkins University, Recently,Gott et al.(2006)measuredthegenusstatis- the Joint Institute for Nuclear Astrophysics, the Kavli tic from a large sample of the SDSS galaxies and Institute for Particle Astrophysics and Cosmology, the compared it with those of mock galaxies created by Korean Scientist Group, the Chinese Academy of Sci- the three distinctive methods such as the semi-analytic ences(LAMOST), LosAlamos NationalLaboratory,the galaxy formation model applied to the Millennium run Max-Planck-Institute for Astronomy (MPIA), the Max- (Springel et al. 2005), a hydrodynamic simulation, and Planck-Institute for Astrophysics (MPA), New Mexico thesubhalo-galaxycorrespondencemodeladoptedinthis State University, Ohio State University, University of paper. It was found that the observed topology of large Pittsburgh, University of Portsmouth, Princeton Uni- scale structure was best reproduced by the subhalo- versity, the United States Naval Observatory, and the galaxy correspondence model even though other models University of Washington. were also consistent with the observation. However, the The authors would like to acknowledge the use of the observed topology was marginally inconsistent with all linux cluster, QUEST, at the Korea Institute for Ad- simulations in the sense that it showed a strong meat- vanced Study (KIAS). Its huge computing power is in- balltopologyatthe significancelevelof2.5σ atthe scale dispensible forthe study,andwethank the systemman- studied. The prominence of the isolatedhigh density re- agers for their efforts in providing a stable and comfort- gions in the observation seems to be due to the Sloan able computation resources during the simulation and Great Wall which was a dominant structure in the sam- subsequent analysis. REFERENCES Abazajian,K.,Zheng,Z.,Zehavi,I.,Weinberg,D.H.,Frieman,J.A., Cole,S.,Aragon-Salamanca,A.,Frenk,C.S.,Navarro,&Zepf,S.E. Berlind, A.A., Blanton, M.R., Bahcall, N.A., Brinkmann, J., 1994,MNRAS,271,781 Schneider, D.P.,&Tegmark,M.2005,ApJ,625,613 Conroy,C.C.,Wechsler,R.H.,&Kravtsov,A.V.2006,ApJ,647,201 Baugh,C.M.2006,ReportonProgressinPhysics,69,3101 Cooray,A.2005,MNRAS,363,337 Berlind,A.A.&Weinberg,D.H.2002, ApJ,575,587 Dubinski,J.,Kim,J.,Park,C.,&Humble,R.2003,NewAstronomy, Blantonetal.2001,AJ,121,2358 9,111 Blanton,M.R.&Roweis,S.2007,ApJ,133,754 Eke,V.R.,Baugh,C.M.,Cole,S.,Frenk,C.S.,&Navarro,J.F.2006, vandenBosch,F.C.,Yang,X.,&Mo,H.J.2003,MNRAS,340,771 MNRAS,370,1147 Cervantes-Sodi, B., Hernandez, X., Park, C., & Kim, J. 2007, Evans,N.W.&Wilkinson,M.I.2000,MNRAS,316,929 arXiv/0712.0843