Table Of Content

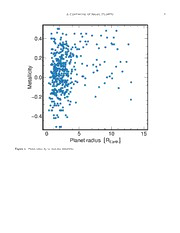
ApJL in press PreprinttypesetusingLATEXstyleemulateapjv.05/12/14 A CONTINUUM OF SMALL PLANET FORMATION BETWEEN 1 AND 4 EARTH RADII Kevin C. Schlaufman1,2 1 KavliInstituteforAstrophysicsandSpaceResearch,MassachusettsInstituteofTechnology,Cambridge,MA02139,USA; [email protected] Received 2014 November 14; accepted 2014 December 31 ABSTRACT It has long been known that stars with high metallicity are more likely to host giant planets than stars with low metallicity. Yet the connection between host star metallicity and the properties of 5 smallplanetsisonlyjustbeginningtobeinvestigated. Ithasrecentlybeenarguedthatthemetallicity 1 distributionofstarswithexoplanetcandidatesidentifiedbyKepler providesevidenceforthreedistinct 0 clusters of exoplanets, distinguished by planet radius boundaries at 1.7R and 3.9R . This would ⊕ ⊕ 2 suggestthattherearethreedistinctplanetformationpathwaysforsuper-Earths, mini-Neptunes, and giantplanets. However,asIshowthroughthreeindependentanalyses,thereisactuallynoevidencefor n theproposedradiusboundaryat1.7R . Ontheotherhand,amorerigorouscalculationdemonstrates a ⊕ J thatasingle, continuous relationshipbetweenplanet radius andmetallicityis abetterfittothe data. The planet radius and metallicity data therefore provides no evidence for distinct categories of small 3 planets. This suggests that the planet formation process in a typical protoplanetary disk produces a 2 continuum of planet sizes between 1R and 4R . As a result, the currently available planet radius ⊕ ⊕ ] and metallicity data for solar-metallicity F and G stars give no reason to expect that the amount of P solidmaterialinaprotoplanetarydiskdetermineswhethersuper-Earthsormini-Neptunesareformed. E Keywords: methods: statistical — planetary systems — planets and satellites: formation — stars: h. statistics p - o 1. INTRODUCTION small-planet and large-planet subsamples for different r The probability that a giant planet orbits a star is a choices of the radius boundary dividing the two sub- t samples. They calculated the p-value from a two-sample s steeplyrisingfunctionofthehoststar’smetallicity(e.g., a Kolmogorov–Smirnov test on the two subsamples as a Santos et al. 2004; Fischer & Valenti 2005). This obser- [ function of planet radius and identified local minima p- vation is the key piece of evidence that the giant planets values. They saved the radii at which the local min- 1 identified by the radial velocity and transit techniques ima occurred. To account for measurement uncertain- v form through core accretion and not through gravita- ties, they repeated this process 106 times, sampling the 3 tional instability. This observation is perhaps the most planet radius and host star metallicity from their uncer- 5 important constraint placed on models of planet forma- tainty distributions on each iteration. They identified a 9 tion since the discovery of the first exoplanets. 5 The connection between stellar metallicity and the distinct p-value minimum at Rp = 1.7R⊕ and argued 0 presenceofsmallplanetsislessclear. TheNeptune-mass that it represents a boundary between terrestrial and 1. planets discovered by radial velocity surveys do not ap- “gas dwarf” planets. This approach is inappropriate be- cause it performs a large number of hypothesis tests on 0 pear to preferentially orbit metal-rich FGK stars (e.g., the same data set without correcting the test thresholds 5 Sousa et al. 2008; Mayor et al. 2011). While Kepler to account for the large number of tests. That strat- 1 has discovered a large number of small exoplanet can- egyisknowntoproduceahighfalse-discoveryrate(e.g., : didates (planets from here), it has not yet settled the v Dunn 1959, 1961). Moreover, the B14 technique creates issue. Schlaufman & Laughlin (2011) showed that while i a sequence of p-values at many split points for data sub- X the giant planets discovered by Kepler orbit metal-rich ject to measurement uncertainty. Consequently, before stars, the small planets discovered around F and G stars r attachinganysignificancetofeaturesinthatsequenceof a did not appear to prefer metal-rich stars. This observa- p-values,itisalsocriticaltoensurethatthep-valuesthat tion was later confirmed by Buchhave et al. (2012). result from the Monte Carlo simulation accurately rep- Recently, Buchhave et al. (2014) (B14 from here) ar- resent the p-value measurement uncertainties that result gued that the observed distribution of metallicity in a from uncertainties in the input sample. sample of more than 400 Kepler planet host stars re- There are at least four more problems with the analy- vealed three distinct clusters of exoplanets: terrestrial planets with planet radius R (cid:46) 1.7R , “gas dwarf” sis presented in B14. First, B14 overlooked the effect planets with 1.7R (cid:46) R (cid:46) 3p.9R , an⊕d ice or gas gi- of planet radius uncertainty due to transit depth un- ants with R (cid:38)3.9⊕R . Tphey sugge⊕sted that these three certainty. Second, their approach used an asymptoti- p ⊕ callyinconsistentestimatoroftheaveragep-valueateach populations formed via distinct planet formation chan- split point in the presence of observational uncertainty. nels. Third, their analysis is subject to the multiple compar- To reach that conclusion, B14 repeatedly split their isonsproblem,whichreducesthesignificanceoftheirob- sampleofplanethoststarmetallicitymeasurementsinto servation by a large amount. Fourth, while B14 assert 2KavliFellow. that local minima in a plot of p-value as a function of 2 Schlaufman splitradiusindicatetransitionsbetweendistinctclusters Monte Carlo iterations, they determined the mean radii of exoplanets, this is not necessarily so. I describe my atwhichlocalp-valueminimaoccurredbyaveragingover sampleselectioninSection2,Idetaileachissuewiththe theindividualradiicalculatedoneachiteration. Inother B14 calculation in Section 3, I outline a more rigorous words, they applied the nonlinear function f that takes way to investigate the issue in Section 4, and I discuss a sequence of p-values and identifies the radii of local the implications and my conclusion in Section 5. p-value minima before averaging over all iterations to identify the mean radii at which p-value minima occur. 2. SAMPLECONSTRUCTION Thecentrallimittheoremdoesnotapplyinthiscase,as I use the planet host star data from B14. Those data f(p(cid:48))=f(cid:0)p+N(0,σ2)(cid:1), (6) include T ,logg, [M/H], M , R , and their associated eff ∗ ∗ uncertainties. B14 did not include in their planet radius E[f(p(cid:48))]=E(cid:2)f(cid:0)p+N(0,σ2)(cid:1)(cid:3), (7) uncertainties the effect of uncertainties in transit depth, n n even though transit depth uncertainties are more impor- 1 (cid:88)f(p(cid:48))= 1 (cid:88)f(cid:0)p+N(0,σ2)(cid:1), (8) tantthanthehoststarradiusuncertaintiesin25%ofthe n n i=1 i=1 sample. As aresult, I supplementthe B14 datawith the latest Kepler object of interest period and R /R esti- f(p(cid:48))=f(p+N(0,σ2))(cid:54)⇒f(p(cid:48))=f(p). (9) p ∗ matesfrom theKepler CasJobsdatabase2 hostedby the As a result, the p-values in their Figure 1 improperly MikulskiArchiveforSpaceTelescopes. Ithenrecompute account for measurement uncertainty and are asymptot- planet radii from the B14 stellar radii and the updated icallyinconsistentwiththetruep-valuesabsentmeasure- transitdepths. FollowingB14,Iremovefromthesample ment uncertainty. all planets smaller than 3R⊕ subject to strong stellar To address that problem, I first generate 105 realiza- irradiation (i.e., F >5×105 J s−1 m−2), as these plan- ν tionsofeachplanetradiusfromthedistributionsthatre- ets may have lost a significant fraction of their initial sult from the propagation of measurement uncertainties atmospheres. I plot these data in Figure 1. inR andR /R . Isplitthemetallicitydataintosmall- ∗ p ∗ planet and large-planet subsamples at 321 split points 3. ISSUESWITHTHEBUCHHAVEETAL.(2014) from0.3to13.1R instepsof0.04R andcomputethe CALCULATION ⊕ ⊕ p-value from a two-sample Kolmogorov–Smirnov test. I 3.1. An Asymptotically Inconsistent p-value Estimator save the resulting p-value for each split point and repeat Anasymptoticallyinconsistentestimatorofaparame- this process 105 times. At the end of the calculation, I ter does not converge to the true value of the parameter average the p-values for each split point. I plot the re- in the large-sample limit. One problem with the B14 sult in Figure 2. The apparent local minimum in the analysis is that they used an asymptotically inconsistent p-value distribution identified by B14 at R = 1.7R is p ⊕ estimatorofthep-valueaveragedoverplanetradiusmea- not present. surement uncertainty in their Monte Carlo simulation. The p-value measurements depend on the planet radius 3.2. The Multiple Comparisons Problem measurements,whicharesubjecttomeasurementuncer- Another issue involves the multiple comparisons prob- tainty in the inferred stellar radii R and the measured ∗ lem. The multiple comparisons problem occurs in sta- ratios R /R . The true p-values in the absence of un- p ∗ tistical analyses when the same data is both used to certainty cannot be measured directly. Instead, one can select a model and estimate its parameters (e.g., Ben- only measure p(cid:48) jamini2010). Itfrequentlyleadstotheunderestimateof p(cid:48)=p+N(cid:0)0,σ2(cid:1), (1) the uncertainty of the model parameters. In this case, B14 used the same metallicity data to both identify the where p is the true p-value and N(0,σ2) is due to mea- planet radius boundaries that separated the three dis- surement uncertainties in R and R /R . Repeatedly tinct clusters and to estimate the mean metallicity and ∗ p ∗ calculating p(cid:48) after perturbing each planet radius due to associated uncertainty for each cluster. Since they used theuncertaintiesinR andR /R andaveragingthere- their data both to set the boundaries and determine the ∗ p ∗ sultwillprovideanasymptoticallyconsistentestimateof mean metallicities for each region, their analysis is sub- p by the central limit theorem ject to the multiple comparisons problem. One way to correct for this problem is to use indepen- E[p(cid:48)]=E(cid:2)p+N(0,σ2)(cid:3), (2) dentdatasets,onetoselectthemodelandanothertofit E[p(cid:48)]=E[p]+E(cid:2)N(0,σ2)(cid:3), (3) themodelparameters. Inthiscase,thecorrectapproach is to split the metallicity data in half. The first half 1 (cid:88)n 1 (cid:88)n 1 (cid:88)n should be used to identify the planet radius boundaries p(cid:48)= p+ N(0,σ2), (4) that separate the three distinct clusters of exoplanets. n n n i=1 i=1 i=1 The second half should then be used to infer the aver- p(cid:48)=p+0⇒p(cid:48) =p. (5) age metallicity of each proposed cluster. This process can be repeated a large number of times with different B14neveraveragedthep-valueproducedforeachsplit randomly selected subsamples. Consequently, on each point over all iterations. Instead, after each iteration iteration of a Monte Carlo simulation, I split the data of their Monte Carlo simulation they identified the local set described in Section 2 in half. I follow the approach p-value minima and saved them. After completing 106 of B14 and identify p-value minima at R < 2R and p ⊕ 2R <R <4R . Iusethoseplanetradiiasthebound- ⊕ p ⊕ 2 http://mastweb.stsci.edu/kplrcasjobs/ ariesofeachexoplanetclusterandusethesecondhalfof A Continuum of Small Planets 3 (cid:26) (cid:27) the metallicity data to compute the mean metallicity of exp −1(x −µ )TΣ−1(x −µ ) (.12) each cluster. I repeat this process 105 times. I find that 2 i j j i j thedifferencebetweenthemeanmetallicitiesfortheter- Here µ and Σ are the mean and covariance of each restrialand“gasdwarf”regionsisonly0.7σ—muchlower j j of the m components of the model. I fit the Gaussian than the 3.1σ offset reported by B14. Metal-poor stars are smaller than metal-rich stars, so mixture models using the mclust3 package in R4 (Fraley & Raftery 2002; Fraley et al. 2012; R Core Team 2014). a bias toward finding small planets around metal-poor To account for the observational uncertainties, I use stars in a transit-depth-limited survey is a systematic a Monte Carlo simulation. I sample the planet radii effect that will further decrease the significance of this from the distributions that result from the propagation offset (Gaidos & Mann 2013). The fact that the mean of measurement uncertainties in R and R /R and di- metallicities of the stars on either side of the claimed ∗ p ∗ rectly use the measured metallicities (since the uncer- transition at R = 1.7R are indistinguishable contra- p ⊕ tainty in [M/H] is already reflected in the uncertainty in dictstheB14interpretationofthetransitionasevidence R ). On each iteration, I fit linear models of the form of of different planet formation pathways. ∗ Equation (10) for m = 1,2,...,5 and Gaussian mixture modelsm=1,2,...,7. Ichooseboththebestlinearand 3.3. Do Local p-value Minima Indicate Distinct GaussianmixturemodelsusingtheBayesianinformation Exoplanet Regimes? criterion(BIC;Schwarz1978),thenusetheAkaikeinfor- While B14 argue that local minima in a plot of split mation criterion (AIC; Akaike 1974) to choose between radius versus p-value indicate transitions between dis- the favored linear and Gaussian mixture models. I re- tinct exoplanet clusters, this is not always the case. To peat this process 103 times. In all cases, the best linear demonstrate this, I use the same Monte Carlo simula- model is preferred. For the linear model, the m = 1 tion described in Section 3.1. However, instead of using model is favored 76.4% of the time, the m = 2 model is the observed metallicities, on each iteration I randomly favored 22.3% of the time, while a higher-order model is sample the metallicities of stars hosting planets with favored 1.3% of the time. While the Gaussian mixture R ≤ 1.7R , 1.7R < R ≤ 3.9R , and R ≥ 3.9R p ⊕ ⊕ p ⊕ p ⊕ modelisdisfavoredrelativetothelinearmodel, thetwo- from their observed distributions. Those distributions component model is the best of the mixture models: the are N(0.00,0.202), N(0.05,0.192), and N(0.18,0.192). I two-component model is preferred on 92.8% of the itera- plottheresultinFigure3. Despitethefactthatdistinct tions,whilethethree-componentmodelispreferred7.2% metallicity distributions were imposed on each planet of the time. I plot representative examples of the BIC- cluster, there is no local minimum in the p-value distri- selected models from one iteration of my Monte Carlo bution at the boundary between the terrestrial and “gas simulation in Figure 4. dwarf” planets. The inability of the B14 technique to identify a metallicity boundary imposed by construction 5. DISCUSSIONANDCONCLUSION as a local p-value minimum implies that the technique is Theperformanceofalargenumberoftestsonthesame not sensitive to subtle features in the metallicity distri- datasetwithoutcorrectingthetestthresholds,theuseof bution. anasymptoticallyinconsistentestimatorofthep-valuein the presence of measurement uncertainty, the oversight 4. AMORERIGOROUSAPPROACH of the multiple comparison problem, or the inability of Abetterwaytoidentifythenumberofsubpopulations the B14 technique to identify an imposed metallicity ef- required by the planet radius and host star metallicity fect as a p-value minimum are all sufficient reasons to data is to compare statistical models with varying num- be skeptical of the claimed transition at R = 1.7R . bersofcomponents,thenidentifythemodelthathasthe p ⊕ The problems with the B14 analysis technique cannot minimum number of parameters yet the maximum like- be mitigated by examining a larger or independent data lihood of producing the observed data. I consider two set—they are inherent in the analysis technique itself. classes of models. First, I fit single-population linear Instead, the analysis in Section 4 shows that a smooth, models of the form one-component linear model is a better fit to the data m than any multi-component model. If a multi-component (cid:88) [M/H]=a0+ ajRpj +(cid:15), (10) model is used, then the two-component model is consis- j=1 tently a better fit than the three-component model. As a result, the planet radius and metallicity data for the where(cid:15)isthestandarduncertaintytermintheregression Kepler F and G star planet hosts does not support the equation. Second, I fit finite Gaussian mixture models idea of multiple types of small planets. Instead, a con- with varying numbers of subpopulations of the form tinuum of planet sizes between 1R and 4R are likely ⊕ ⊕ n m formed independent of the amount of solids present. (cid:89)(cid:88) w N (x |µ ,Σ ), (11) While observational evidence suggests that most plan- j j i j j ets larger than about 2R have significant hydrogen at- i=1j=1 ⊕ mospheres (e.g., Marcy et al. 2014), Kepler-10c is an ex- where x is the data, m is the number of components in ception with a radius of 2.35R and a density of 7.1 g the model, the wj are weights such that (cid:80)mj=1wj = 1, cm−3 (Dumusque et al. 2014). L⊕ikewise, smaller planets and each N is a two-dimensional Gaussian component probably have a wide range of atmospheric properties j of the overall density 3 http://www.stat.washington.edu/mclust/ 1 N (x|µ ,Σ )= × 4 http://www.R-project.org/ j j j 2π|Σ |1/2 j 4 Schlaufman (e.g., Rogers 2014; Wolfgang & Lopez 2014). Moreover, Facilities: Kepler awiderangeofdensitiescanbepresenteveninthesame system, with Kepler-36 the best example (Carter et al. REFERENCES 2012). For these reasons, near solar metallicity it does not seem likely that the final masses or compositions of Akaike,H.1974,ITAC,19,716 Benjamini,Y.2010,Biom.J.,52,708 small exoplanets are controlled primarily by the amount Buchhave,L.A.,Bizzarro,M.,Latham,D.W.,etal.2014, of solid material present in their parent protoplanetary Natur,509,593 disks. Buchhave,L.A.,Latham,D.W.,Johansen,A.,etal.2012, Natur,486,375 Carter,J.A.,Agol,E.,Chaplin,W.J.,etal.2012,Sci,337,556 Dumusque,X.,Bonomo,A.S.,Haywood,R.D.,etal.2014,ApJ, 789,154 Dunn,O.J.1959,Ann.Math.Statist.,30,192 Dunn,O.J.1961,J.Am.Stat.Assoc.,56,64 Fischer,D.A.,&Valenti,J.2005,ApJ,622,1102 Fraley,C.&Raftery,A.E.2002,J.Am.Stat.Assoc.,97,611 I thank Lars Buchhave, Andy Casey, Bryce Croll, Fraley,C.,Raftery,A.E.,Murphy,T.B.,&Scrucca,L.2012, David W. Latham, Dimitar Sasselov, and Josh Winn. mclustVersion4forR:NormalMixtureModelingfor I am especially grateful to the referee Eric Feigelson for Model-BasedClustering,Classification,andDensity suggestionsthatsubstantiallyimprovedthispaper. This Estimation,TechnicalReportNo.597(Seattle,WA:Univ. Wash.Dept.ofStatistics) researchhasmadeuseofNASA’sAstrophysicsDataSys- Gaidos,E.,&Mann,A.W.2013,ApJ,762,41 tem Bibliographic Services. Some of the data presented Koenker,R.,quantreg:QuantileRegression.Rpackageversion in this paper were obtained from the Mikulski Archive 5.05(Champaign,IL:Univ.ofIllinois) for Space Telescopes (MAST). STScI is operated by the Marcy,G.W.,Isaacson,H.,Howard,A.W.,etal.2014,ApJS, Association of Universities for Research in Astronomy, 210,20 Mayor,M.,Marmier,M.,Lovis,C.,etal.2011,arXiv:1109.2497 Inc., under NASA contract NAS5-26555. Support for RCoreTeam2014,R:ALanguageandEnvironmentfor MASTfornon-HSTdataisprovidedbytheNASAOffice StatisticalComputing(Vienna:RFoundationforStatistical of Space Science via grant NNX13AC07G and by other Computing) grants and contracts. This paper includes data collected Rogers,L.A.2014,arXiv:1407.4457 by the Kepler mission. Funding for the Kepler mission Santos,N.C.,Israelian,G.,&Mayor,M.2004,A&A,415,1153 Schlaufman,K.C.,&Laughlin,G.2011,ApJ,738,177 is provided by the NASA Science Mission directorate. Schwarz,G.E.1978,AnSta,6,461 Support for this work was provided by the MIT Kavli Sousa,S.G.,Santos,N.C.,Mayor,M.,etal.2008,A&A,487,373 InstituteforAstrophysicsandSpaceResearchthrougha Wolfgang,A.,&Lopez,E.2014,arXiv:1409.2982 Kavli Postdoctoral Fellowship. A Continuum of Small Planets 5 ll l l l l l l l l l l l l l 0.4 lll l l l l l l l l ll l l l l l l llll l l l ll l lll l l l ll l l l l l lll l ll l l l ll l l l l l l ll ll llllll l l ll ll l ll l l l l l l l l l 0.2 l llllll lll l llllll ll l l l lllll l ll l l l l llllllll l l ll lllllll l l llll l l l l l l lllll l y llllllll llllll l l l llllllll l l it l llllllllllllllllllllll ll l ll l c lllllllllllll l l l i llllllllllllllll l all 0.0 llllllllllllllllllllllllllll l l lll l ll l l llllll t llllllll lllllllllllll l ll l e ll l llllll llll l l l l ll l M lll lll l ll l l ll l llllll lll ll l l llll ll lll ll l lllll llll llllll l l llll l l −0.2 l ll l l l l ll lll ll l l llll l l l ll l l l lll l l lll llll −0.4 l l l l l lll l ll 0 5 10 15 [ ] Planet radius R Earth Figure 1. PlanetradiusRp vs. hoststarmetallicity. 6 Schlaufman 0 10 G 10- 1 llllllllllllllllllllllllllllllllllllllll as dw llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll llllllll arfs llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll 10- 2 llll ? llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll ue llllll llllllllllllllllllllllllllll -pval 1100-- 43 llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll ll ll Te llllllllllllllllllllllllllllllllllllllllllllllllllllllllll r r - 5 e 10 s t Ice/gas giants r i a l ? - 6 10 0 2 4 6 8 10 12 14 [ ] Planet radius R Earth Figure 2. Meanp-valueasafunctionofplanetradius. Isplitthesampleintosmall-planetandlarge-planetsubsamplesat321splitpoints from 0.3R⊕ to 13.1R⊕ in steps of 0.04R⊕ and compute the p-value from a two-sample Kolmogorov–Smirnov tests on the metallicity distributions of both subsamples. I repeat this process 105 times. The black points are mean p-values averaged over the uncertainties in hoststarradiusR∗ andtransitdepth(Rp/R∗)2. Iindicatetheuncertaintyateachradiusasasemi-transparentgrayrectanglewithheight given by the uncertainty in the p-value and width 0.02R⊕. After accounting for the uncertainties in R∗ and (Rp/R∗)2, the p-values do notsupporttheideaofaqualitativedifferencebetweenplanetswithradiiaboveorbelow1.7R⊕. A Continuum of Small Planets 7 0 10 G -pvalue 1111100000----- 54321 Terrestrllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllas dwarfs?llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllIllllllllcllllllllllllllellllllllllllll/llllllllgllllllllllllllllallllllllllllllllsllllllllllllll llllllllgllllllllllllllillllllallllllllllllllllnlllllllllllllllltllllllllsllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll i a l ? - 6 10 0 2 4 6 8 10 12 14 [ ] Planet radius R Earth Figure 3. Mean p-value as a function of planet radius in the scenario advocated by B14 for three distinct planet clusters separated at 1.7R⊕ and3.9R⊕ withmetallicitydistributionsN(0.00,0.202),N(0.05,0.192),andN(0.18,0.192). Ifplanetradiusboundariesat1.7R⊕ and 3.9R⊕ do separate the exoplanet population into three clusters with unique metallicity distributions, then that difference would manifestitselfasanon-continuousfirstderivative—a“kink”—at1.7R⊕. Eventhoughthreeuniquemetallicitydistributionwereimposed byconstructioninthiscase,thereisnop-valueminimumat1.7R⊕. Consequently,eveniftherewerethreedistinctclustersofexoplanets, eachwithauniquemetallicitydistribution,theanalysisdescribedinB14wouldnotbeabletoidentifythembyp-valueminima. 8 Schlaufman ll ll l l 0.4 llllllll ll lllll l l l 0.4 llllllll ll Metallicity−000...202 llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll lllllll llllllllllllllllll llll Metallicity−000...202 lllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll l l l l lll llll lll llll −0.4 lllllll l −0.4 lllllll l l ll l ll 0 5 10 15 0 5 10 15 Planet radius [R ] Planet radius [R ] Earth Earth Figure 4. Two different models for the relationship between Rp and metallicity. Left: a one-component, linear relationship between Rp and metallicity. The blue line shows the best-fit model, while the green-shaded region shows the 25% and 75% quantile regression bands computed using the quantreg package (Koenker 2013). Right: a Gaussian mixture model with two components. Planets plotted as blue circles are assigned to one component, while gray squares are assigned to the other. The divide between the two populations occurs at Rp ≈4R⊕. While the two-component Gaussian mixture model is favored over mixture models with one to seven components, theone-componentlinearmodelisfavoredbytheAkaikeinformationcriterion(AIC)overanyofthemixturemodels. Forthatreason, a one-componentsmoothmodeliscurrentlythebestmatchtotheKepler planetradiusandmetallicitydataforFandGstarspresentedin B14.