On Doppler Ultrasonic Measurements of the Blood Flowing Through Vessels

6 Pages·1.106 MB·English

by  Prodeus A. et al.

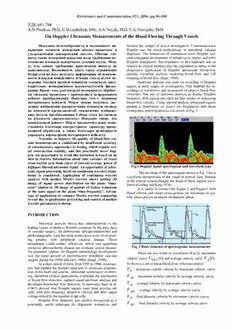
Electronics and Communication, #21, 2004, pp.94-100
УДК 681.784
A.N.Prodeus, PhD, U.B.Lushchyk, DSc, S.A.Nayda, PhD, E.G.Nesvijski, PhD
On Doppler Ultrasonic Measurements of the Blood Flowing Through Vessels

Показаны целесообразность и возможность по- became the subject of active investigation. Continuous-wave
вышения точности измерений объема кровотока в Doppler was the initial methodology in peripheral vascular
ультразвуковой доплеровский системе. Обычно точ- diagnosis. The limitations of continuous-wave Doppler sys-
ность таких измерений невысока из-за требования по- tems stimulated development of pulsed-wave, duplex and color
стоянства площади поперечного сечения сосуда. Меж- Doppler instruments. Developments of this approach and its
ду тем, данное требование практически никогда не relation to clinical interests may be considered in terms of the
выполняется. Возможность снять такое ограничение progressive application of Doppler ultrasound: blood-flow
базируется на идее получать информацию об изменчи- sensing, waveform analysis, localizing blood flow, and 2-D
вости площади поперечного сечения сосуда путем из- mapping of blood flow (Sigel, 1998).
мерения текущей средней мощности эхосигнала, пред- Spectrum analysis was used for recording of Doppler
варительно подверженного высокочастотной фильт- signals at early stages of investigation. This enabled the re-
рации. Кроме того, рассмотрена возможность обработ- cordings of waveforms and assessment of relative blood flow
ки сигналов кровотока с применением непрерывного velocities. The use of spectrum analysis to display Doppler
вейвлет преобразования. Показано, что с помощью frequency shift signals provided the best means of measuring
материнского вейвлета Морле можно получить дву- blood-flow velocity. Using spectral analysis ultrasound signals
мерное изображение распределения мощности сигнала present a distribution of power on frequencies and times
на плоскости время-масштаб, аналогичное изображе- (sonograms, spectrograms) as it is shown in Fig. 1.
нию модуля преобразования Габора этого же сигнала
на плоскости «время-частота». Показано также, что
комплексный вейвлет Морле предпочтительнее веще-
ственного благодаря квадратурному характеру произ-
водимой обработки, а также благодаря возможности
управлять параметрами материнского вейвлета.
Necessity to improve the quality of blood-flow vol-
ume measurements is conditioned by insufficient accuracy
of contemporary approaches to testing, which require ves-
sel cross-section stability, and this practically never hap-
pen. An opportunity to avoid this limitation is based on an
idea to retrieve information about time variance of vessel
cross-section area from curve of current average power of
highpass filtered ultrasonic signal. An opportunity of ultra- Fig.1 Doppler signal spectrogram and waveform type
sonic signal processing based on continuous wavelets trans-
The envelope of the spectrogram shown in Fig. 2 has a
forms is considered. Application of continuous wavelet
waveform characteristic of the vessel in normal state. Disease
analysis with mother Morlet wavelet allows getting 2D
in the arterial system changes the shape of these regular wave-
image of signal power distribution on the plane “time-
forms (Gosling and King 1974).
scale” similar to 2D image of module of Gabor transform
It is useful to connect the Figure 2 and Figure3: both
of the same signal on the plane “time-frequency”. Advan-
blood velocity and vessel cross-sections are maximum on sys-
tage of application of complex Morlet wavelet comparing
tolic phase and are minimum on diastolic phase.
to real due to quadrature processing and control of mother

wavelet parameters is shown.

INTRODUCTION

Statistical analysis shows that atherosclerosis is the
leading causes of death in Western countries. In the early days
of vascular surgery, the stethoscope, sphygmomanometer and
plethysmography were the main noninvasive tools for evaluat-
ing patients with peripheral vascular disease. These
instruments could neither effectively detect and quantitate
occlusive atherosclerotic disease nor evaluate venous disease. Fig. 2 Basic elements of spectrograms measurements
An important impetus for Doppler methodology development
There are two kinds of waveforms (Fig.2): maximum
was the rapid growth or reconstructive peripheral vascular
velocity curve V (t)and average velocity curve V (t).
surgery during the 1950s and early 1960s (Sigel, 1998). MAX A
In a short period of time, from 1956 to 1966, investiga- So there is a set of linear blood-flow velocities (smps):
tors had applied the Doppler principle to ultrasonic examina- V – maximum systolic velocity by maximum velocity curve;
S
tion of the heart and arteries, performed noninvasive monitor-
ing, identified clinical applications, explained the mechanism V – maximum systolic velocity by average velocity curve;
AS
of blood flow detection, applied sound spectrum analysis and
developed directional flow detection. In particular, Kato et al. VM – average velocity by maximum velocity curve;
(1962) showed that Doppler signals were from moving red V – average velocity by average velocity curve;
cells, with their frequency related to velocity and their output AM
voltage related to the number of red cells. V – final diastolic velocity by maximum velocity curve;
D
Doppler flow detection was quickly recognized as a
potentially useful technique for diagnostic evaluation, and VAD – final diastolic velocity by average velocity curve.
Electronics and Communication, #21, 2004, pp.94-100
The volume of blood flowing through a vessel is often where N (t) - noise caused by reflection of practically mo-
of clinical importance. Volume flow measurements made with 1
a uniform insonation technique assume that the sample volume tionless tissues, surrounding a vessel, and N (t) - noise
2
is large compared to the vessel (Fig.3). Martin et al. (2000)
caused by reflection of vessel walls oscillating in the direction
studied the brachial artery volume flow, Schiller and Osipov orthogonal to the direction of blood flow.
(1993) studied echocardiographic parameters and evaluated
As the sample volume does not change in time it is
minute volume flow rate: reasonable to assume that the current average power of the
CO = HR×SV ; (1) signal X(t) also should be practically a constant:
SV = A×VTI ; (2)
t+T
1
VTI = ET×VAM ; (3) PX(t)= ∫X2(t)dt ≈cX , (6)
T
CO – minute volume flow rate; HR – heart ratio; t
SV – stroke volume; A=πD2 4 - measured cross- where T << ET - range of averaging.

sectional area; D – section diameter; VTI – integral of
linear blood-flow velocity on time interval ET ; ET – in-
terval between two neighbor systolic peaks of waveform.
Assumed-profile technique uses a small sample vol-
ume. Multi-gate techniques measure the Doppler shifts along a
vessel diameter and make assumptions about the velocity pro-
file to calculate volume flow. A technique described by Picot
et al. (1995) uses transverse color Doppler images to calculate
volume blood flow and thus eliminates any assumptions about
the velocity profile. However, this method assumes that the
color Doppler sample volumes are small relative to the vessel
diameter. Unfortunately, the accuracy of volume flow meas-
urements made with ultrasound has traditionally been very

disappointing. It has not been shown previously whether im- a)
provements in Doppler instrumentation will improve the accu-
racy of volume flow measurements.
There are some serious restrictions for such measure-
ments. Cross-sectional area of vessel has to be stable during
measurements time (Schiller and Osipov 1993) is one of them.
Of course this condition rarely observed in a real situation, so
such measurements may cause a serious error and, conse-
quently, diagnostic significance of the parameter may be far
from really reachable. So the first goal of this paper is to im-
prove assessment of blood flow volume on the assumption that
the sample volume is large compared to the vessel ignoring the
restriction of stability of cross-sectional area of vessel.
The second goal of the paper is demonstration of use-
fulness of continues wavelet transform (CWT) for processing
b)
of Doppler-shifted ultrasound signals.

Fig.3 Vessel in systolic (a) and diastolic (b) phases
PHYSICAL STATE AND SIGNAL MODELING
As mass of vessel walls is practically constant, current

A simplified model of a blood flow in vessels, where average power of component N2(t) should be also be con-
the area of a vessel cross-section is considered a constant, is stant:
used, and only blood velocity periodically changes (Webb
t+T
1
1988). A more realistic model is considered in this paper. Ac- P (t)= ∫N2(t)dt ≈c . (7)
cording to this model a vessel cross-section periodically varies N2 T 2 N2
with changes in blood flow, synchronously with velocity of t
erythrocytes. Furthermore it is assumed that the size of the On the contrary the curve of current average power of
sample volume is adapted to the vessel diameter to cover it signal component P (t)
entirely – it is right for a uniform insonation technique. Eryth- S
rocytes participating in ultrasonic signal reflections are pre- 1 t+T
sented as areas shaded with crossing horizontal and vertical P (t)= ∫S2(t)dt (8)
S
lines in Fig. 3. T
t
Based on the considered above ultrasonic echo signal
should have very variable form because of the number of
X(t) on receiver output can be presented as the sum:
erythrocytes participating in ultrasonic signal reflections is
X(t)= S(t)+N(t), (4) changing considerably reaching its maximum in systolic phase
and minimum in diastolic phase. That is why maximum of
where S(t) - informative part of echo signal, caused by re-
function P (t) should be reached in systolic phase, and
S
flection from moving erythrocytes. Noise N(t) in turn can
minimum in diastolic phase.
be presented as a two-component formula: Curve of current average power of the component
N(t)= N1(t)+N2(t), (5) N1(t) also should vary in time:
Electronics and Communication, #21, 2004, pp.94-100
t+T The short-time spectrum of the signal component:
1
PN1(t)= T ∫N12(t)dt . (9) 1 t0+T 2
t G (f,t )= ∫S(t)exp(−j2πft)dt (11)
S 0
Taking into account relations (4)-(6) it is possible to T
t
conclude that approximate equality should be executed: 0
P (t)+P (t)≈c , (10) concentrates in the area of Doppler frequency
S N SN
1 1 2v
i.e. maximum of function PN1(t) should be reached in dia- fd = f0(1+ cd ), where f0 - radiation frequency, vd -
stolic phase, and minimum in systolic phase (Fig.3).
average on time-interval T erythrocytes velocity. Periodical
Example of graphs of functions PX(t), PS(t), variations in erythrocytes velocity causes changes in Doppler
frequency:
P (t), P (t) is shown in Fig.4a.
N N
1 2  2v (t)
The function PS(t) is of particular interest among fd(t)= f01+ dc . (12)
other functions considered here because it contains information
It could be observed on a spectrogram as an “enve-
about variation of vessels cross-section in time. There is a
lope” and is named “waveform”.
progressive dependency between power of the echo signal
reflecting from moving erythrocytes and cross-section area of
a vessel.
A brief explanation of the curves of shot-time spec-
trum of the signal X(t) and its components is given in
Fig.4b.

Fig.4 Current average power (a) and short-time spectrums (b) of signal X(t) and its components

Spectrum component of noise N1(t) concentrates in 1 t+T 2
near radiation frequency f0, and spectrum of noise compo- GS(f,t)= T ∫S(t)exp(−j2πft)dt . (13)
t
2v
nent N (t) - near frequency f = f (1+ d0), But it is proposed in this work to analyze current aver-
2 d0 0
c age power P (t), that can be calculated in accordance with
S
where vd0 - velocity of vessel walls movements the available spectrogram:
(v <<v ). ∞
d0 d
P (t)= ∫G (f,t)df . (14)
Thus, the echo signal X(t) should be exposed to S S
−∞
highpass filtration for picking up of signal component S(t) It is based on the assumption that current average
(Kozlov et al 2000). power P (t) is proportional to vessel cross-section area
S
Waveform is “envelope” of spectrogram in classical
Doppler systems analysis: A(t), while waveform only qualitatively reminds function
A(t).
Electronics and Communication, #21, 2004, pp.94-100
So it is possible to assume that application of function
P (t) will give an opportunity to measure blood flow vol-
S
ume without requirements of stable vessel cross-section area.
It is reasonable to expect that application of function P (t)
S
instead of spectrogram waveform might improve diagnostic
meaning of the measured blood flow volume.

IMPROVEMENT OF MEASUREMENTS OF BLOOD-
FLOW VOLUME
a)

It was described above that volume of blood flow ac-
cording to formulae (1)-(3) was measured using spectrogram
until now. Requirement for stability of vessel cross-section
area for all duration of measuring time has been a serious limi-
tation of this approach. This requirement is acceptable for
aortal valve and taking out path of the left ventricle (Schiller
and Osipov 1993). In other cases considerable error of meas-
urement should be expected.
To eliminate this limitation it is proposed to calculate

stroke volume SV using formula (15) instead of formula (2):
b)
ET Fig.5 Ultrasonic echo signal X(t) (a) and current average
SV = ∫A(t)V (t)dt, (15) power P (t) (b)
A X
0 As it is shown in the Fig.5b, current average power of
where V (t) - current average velocity of blood flow; A(t) signal X(t) randomly oscillates around some constant value.
A
- immediate vessel cross-section area. A result of application of a simple highpass filtering
Immediate vessel cross-section area A(t) could be y = x −x
n n n−1
calculated by formula: of the signal X(t) is shown in Fig.6.
A
A(t)= max ⋅P (t), (16)
S
P
Smax
where P - maximum value of curve P (t);
Smax S
A =πD2 4.
max max
Certainly power P (t) of signal S(t) is propor-
S
tional to quantity of erythrocytes in vessel cross-section and
then is proportional to cross-section area A(t).
A
max
Evidently coefficient of proportionality in
P
Smax Fig.6 Blood flow signal S(t) after highpass filtering
formula (16) could be looked upon as calibration factor ap-
plied to transition from curveP (t) to curve A(t). Spectrograms of the signal S(t) are presented in Fig.7.
S
Along with described algorithms (15)-(16), simplified Estimation of current average power PS(t) of signal
algorithm described by formula (17) could be also effective:
S(t), calculated by formula (8), is shown in Fig.8a, and by
SV = A ⋅V ⋅ET , (17)
A AM formula (14) – in Fig.8b.
ET
1
where A = ∫A(t)dt - vessel average cross-section There is no difficulty to see that curves presenting cur-
A
ET rent average power of signal S(t) ant its spectrogram are
0
practically concurrent. Some minore difference between curves
ET
1
in Fig.8a and Fig.8b is determined by sampling frequency
area and V = ∫V (t)dt - average velocity by
AM ET A which is 14000 Hz for Fig.8a and 112.9 Hz for Fig.8b.
0
average velocity curve.
CONTINUOUS WAVELET TRANSFORM OF

ULTRASONIC SIGNALS
SAMPLE OF HIGHPASS FILTERED ULTRASONIC
SIGNAL Wavelet transforms are fairly new mathematical tools,
which can be used to present the changing spectrum of a non-
A part of real ultrasonic echo signal X(t) is shown stationary signal in a time-frequency plane. The area of appli-
cation of wavelet transforms for practical problems is con-
in Fig.5a, and estimation of current average power P (t) of stantly growing, so it is only natural to try this approach in
X
signal X(t), calculated by formula (11), is shown in Fig.5b. ultrasonic Doppler technique.
Electronics and Communication, #21, 2004, pp.94-100
and translating of the mother wavelet function ψ (τ)accord-
ing to the following equation
1 t−τ
ψ (τ)= ψ ( ) (18)
a,t
a a
The continuous wavelet transform (CWT) of a signal
x(τ) using wavelet function ψ (τ), W x, is defined
ψ
through the convolution between x(τ) and analyzing wave-
lets over a finite range of scales as,
∞
a) Wψxa,t = ∫x(τ)ψa*,t(τ)dτ (19)
−∞
where ψ* (τ) indicates the complex conjugate of ψ (τ)
a,t a,t
.If a signal correlates well with the analyzing wavelet, the
wavelet coefficient W x will be large, otherwise, it will
ψ a,t
be small.
A variety of different types of wavelets have been de-
veloped for different analysis purposes. The result of CWT
depends mostly on the choice of a mother wavelet.
CWT could be interpreted as signal filtration with a
special set of filters. For example Morlet wavelets could be
interpreted as set of unit-impulse responses of narrowband
b) filters. Their pattern form is those (Fig.9,10), that a result of
Fig.7 Spectrograms of highpass filtered signal: CWT should rather remind a well-known spectrogram.
a) T=0.073 s; b) T=0.02 s There are two types of Morlet wavelets: real and com-
plex. Mother real Morlet wavelet is described by function

x2
−
ψ(x)=e 2 cos(5x), (20)
and a complex type by function
x2
1 −
ψ&(x;F ,F )= e Fb ⋅ej2πFcx (21)
c b
πF
b
Similarity of formulas (20) and (21) is obvious: real
type of Morlet wavelet is equal to real part of complex Morlet
wavelet accurately to constant when F =2 and
b
5
a) F = ≈0.8. Distinction of kind of wavelet functions
c
2π
(20) - (21) is that complex type allows to control effective
length and infill frequency of mother wavelet.
Real Morlet wavelet graph is presented in Fig.9 , and
real and imagine parts of complex Morlet wavelet are given in
Fig.10a,b (for F =2, i.e. with the same width, but with
b
doubled infill frequency F =1.6.
c
CWT with Morlet wavelets of a part of a real blood
flow response (Fig.5) signal is demonstrated in Fig.11.

b)
Fig.8 Current average power P (t) of signal S(t): a) by for-
S
mula (13); b) by formula (19)
A Wavelet transform is a convolution between the sig-
nal and a set of analyzing wavelets. Wavelets are the scaled
and translated versions of a single function referred to as a
mother wavelet. A mother wavelet ψ (τ) is a well-localized

function in both time and frequency domains. A wavelet Fig.9 Real Morlet wavelet
ψ (τ) at scale a and time t is obtained through scaling
a,t
Electronics and Communication, #21, 2004, pp.94-100
CONCLUSION

Possibilities to improve efficiency of measurements of
blood flow volume are presented. Moreover, expediency of
CWT application for processing of ultrasonic signals of blood
flow is considered in this paper.
Necessity to improve the quality of blood flow volume
measurements is conditioned by insufficient accuracy of con-
temporary approaches to testing, which require vessel cross-
b) section stability, and this practically never happen. An oppor-
tunity to avoid this limitation is based on an idea of exhaustive
use of information containing in spectrogram of ultrasonic
signal. It is proposed to retrieve information about vessel
cross-section area in addition to information about erythro-
cytes velocity. It is shown that evaluation of average current
power of signal processed by highpass filtration contains this
information.
It is demonstrated that average current power of ana-
c)
lyzed signal could be determined in time domain by using of
Fig.10 Complex Morlet wavelet (b – real, c – imagine part) moving mean square of the signal or by calculation of areas of
spectrogram time cross-section. Time constant for integral of
moving mean (near 0.07 second) is experimentally determined.
Application of continuous wavelet analysis with
mother Morlet wavelet allows getting 2D image of signal
power distribution on the plane “time-scale” similar to module
of Gabor transform of the same signal on the plane “time-
frequency”. Advantage of application of complex Morlet
wavelet comparing to real due to quadrature processing and
control of mother wavelet parameters is shown. This quadra-
ture processing makes image more clear and sharp. It is possi-
ble to control resolution in time and scale by modifying of
mother wavelet parameters.

a) REFERENCES

Sigel B. A Brief History of Doppler Ultrasound in the Diagno-
sis of Peripheral Vascular Disease. Ultrasound in Medicine &
Biology. 1998;24;2;169-176.
Gosling R.G., King D.H. Arterial assessment by Doppler-shift
ultrasound. Proceedings of the Royal Society of Medicine
1974;67;447-449.
Martin A.G., Grasty M., Lear P.A. Haemodynamics of bra-
chial arteriovenous fistula development. The Journal of Vascu-
lar Access 2000;1;54-59.
Kato K, Kido Y, Motomiya M, Kaneko Z,Kotani H. On the
mechanism of generation detected sound in ultrasonic flow-
meter. Memoires Inst Sci Res Osaka Univ 1962;19;51-57.
Pourcelot L. Clinical applications of transcutaneous Doppler
examinations. In: Perroneau P. ed. Velocimetrie ultrasonore
b) Doppler. Paris: INSERM, #1974;1975:213-240
Fig.11 CWT of signal S(t): real (a) and complex (b) Morlet Moreno J.A., Mesalles E., Gener J., Tomasa A., Ley A., Roca
wavelets J., Fernández-Llamazares J. Evaluating the outcome of severe
head injury with transcranial Doppler ultrasonography. Neuro-
Comparing Fig.11a and Fig.11b, it is possible to see surgical Focus 8 (1): Article 8, 2000
advantages of complex Morlet wavelet: 1) the image is more Schiller N.B., Osipov M.A. Clinic echocardiography.
clear and sharp; 2) image quality can be controlled by parame- Moskow, Mir, 1993
ters of mother wavelet. Kozlov V.A., Artiushenko N.K., Shalak O.V., Girina M.B.,
Morover, comparing Fig.11 with spectrogram of the Girin I.I., Morozova E.A., Monastyrenko A.A. Ultrasonic
same signal in the Fig.8 it is possible to notice their similarity, Doppler echography in assessment of haemodynamics of neck,
that is obvious because frequency f and scale multiplier a face and mouth in norm and some pathologic states. St-
Peterburg, SP Minimax, 2000
are connected by relation a =1 2πf . Webb S. The Physics of Medical Imaging. Adam Hilger, Bris-
Thus, the application of CWT together with Morlet tol and Philadelphia 1988; 633
wavelet brings to the results similar with application of short-
term Fourier transformation with a Gaussian window, i.e. Ga-
bor transform.