1 minute parity lifetime of a NbTiN Cooper-pair transistor

6.2 MB·English

by  David J. van Woerkom

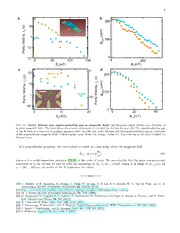
1 minute parity lifetime of a NbTiN Cooper-pair transistor
David J. van Woerkom,∗ Attila Geresdi∗,† and Leo P. Kouwenhoven
QuTech and Kavli Institute of Nanoscience, Delft University of Technology, 2600 GA Delft, The Netherlands.
The parity modulation of the ground state of a a V b
g
superconducting island is a direct consequence of Si/SiO2 2N-1 N N+1
the presence of the Cooper pair condensate pre- Al NbTiN Al Ec 1 τ
ferring an even number of charge carriers [1, 2]. E/ p
5
The addition energy of an odd, unpaired quasi-
1 particle equals to the superconducting gap, ∆, Ibias 0
0
2 suppressing single electron hopping in the low -1 0 1
n
n temperature limit, kBT (cid:28) ∆. Controlling the Counts 0 50 100 g
a quasiparticleoccupationisoffundamentalimpor- c 3.0 d
J tance for superconducting qubits as single elec- 1 τp
6 tron tunneling results in decoherence [3, 4]. In A) max
1 pliaesrtiocnultahre, tpoaproitloygiccoanltqroulanatnudmrecaodmopuuttoaftioMnarjoe-- I(nsw2.0 I/Ic c,0.5
]
n rana bound states [5, 6]. Here we present parity 1.0
o modulation for the first time of a niobium titan- -1 0 1 -1 0 1
c ite nitride (NbTiN) Cooper-pair transistor cou- n n
- g g
r pled to aluminium (Al) leads. We show that this
p
circuit is compatible with the magnetic field re- FIG. 1. Device layout and parity-dependent switch-
u
quirement B ∼100mT of inducing topological su- ing current. (a) Scanning electron microscope image and
s
. perconductivity in spin-orbit coupled nanowires schematic cross-section of a typical Al/NbTiN/Al hybrid
at [7–9]. Our observed parity lifetime exceeding 1 Cooper-pairtransistor(CPT).TheNbTiNislanddimensions
m minuteisseveralordersofmagnitudehigherthan are 250nm×450nm. Scale bar denotes 200nm. The AlOx
oxide barriers are indicated by thick red lines. (b) Energy
- the required gate time of flux-controlled braid-
d level diagram as a function of the gate charge, ng, in the
n ing of Majorana states [10]. Our findings readily presenceoflowenergysubgapstatesrestoring1e periodicity.
o demonstrate that a NbTiN island can be parity- Gray lines denote energy levels in the absence of Josephson
c controlledandthereforeprovidesagoodplatform coupling, i.e. EJ =0. Red and blue lines show energy levels
[ for superconducting coherent circuits operating forevenandoddchargeparityrespectively,bothforEJ =Ec.
1 in a magnetic field. Parity switches occur on the timescale of τp due to quasipar-
ticle tunneling. Measured switching current histogram (c)
v Experimentally, the parity modulation of a supercon-
andcalculatedI (n )(d)inthelowtemperaturelimit. Note
5 ducting island can be observed via the ground state c g
that in (d) the two possible I (n ) values corresponding to
5 c g
charge [2], the even-odd modulation of the charge sta- theevenandoddchargestatesdenotedbyblueandredlines
8
bility diagram [11, 12], or the parity dependence of the respectively. In the measured data (c) the two branches are
3
0 switching current, Isw [13]. The interplay of the charg- superimposed, see text.
. ing energy E = e2/2C and the Josephson coupling
1 c
0 EJ = Ic¯h/2e makes the Cooper-pair transistor (CPT) a
5 single, gate-modulated Josephson junction [13, 14] with rial properties [17], in accordance with earlier measure-
1 a 2e charge periodicity in the absence of parity switches, ments showing that subgap quasiparticle states may ap-
v: i.e. infinitely long parity lifetime, τp. pear in niobium due to oxidization of the bulk material
i Recent, direct measurements of τ [4, 15] yielded val- [19]. In contrast, nitridized niobium compounds, such as
X p
ues up to the millisecond regime for aluminium devices. niobiumtitanitenitride(NbTiN),havebeenshowntobe
ar Despite considerable efforts, however, no 2e periodic- less prone to form oxides and hence are good candidates
ity has been reported for non-aluminium superconduc- for parity-conserving superconducting circuits. Further-
tors[16–18],suchasniobiumorvanadium. Comparative more, NbTiN forms transparent contacts with spin-orbit
studies of aluminium and niobium CPTs suggested that coupled semiconductor nanowires [9], and has become a
the elusiveness of parity effects is related to the mate- preferredsuperconductortoinvestigateMajoranabound
states.
Our device features a NbTiN island sputtered onto Al
leads (Fig. 1a). The tunnel barriers between the island
∗ Theseauthorscontributedequallytothiswork. and the leads are created by means of controlled in-situ
† Correspondingauthor,e-mailaddress: [email protected] surface oxidization of Al, resulting in amorphous AlO
x
2
t (ms)
a 1.0 2.0 b Counts e
102 dI 102
= 1.2μA/s
dt fast
T=25mK I (t) Aluminium NbTiN
s fast bias 10 ρ ρ
nt10 Al NbTiN
u
Co 11.0 2.0 3.0 τp sloIbwiaTs(itm) e τ me, (s)p101-1 S1 ΔAl nqp ρsubgap ΔN bTiN
Isw(nA) eti 24μeV
c 500 t (s)600 700 d 2.5 t (ms) 5.0 y lif10-2 N
102 dI= 1.73pA/s 103 dI = 300nA/s Parit 18μeV 210μeV
dt dt 10-3
nts T=12mK nts102 S2
u10 slow u
o o 10-4
C C 10 100mK
80mK
parity
1 switches 1 70mK 10-5 170μeV
1.0 1.2 1.0 1.5 0 50 100 150
I (nA) I (nA) T (mK)
sw sw
FIG. 2. Characterization and temperature dependence of the parity lifetime. (a) Linecut histogram at integer n
g
of Fig. 1c showing a bimodal distribution. We attribute the two peaks to the two parity states of the CPT (colored red and
blue, respectively). (b) For a fast current ramp (upper panel), the histograms of the two parity states are independently
probedshowingthecharacteristicsofdatainpanel(a). Intheslow limit(lowerpanelin(b)),parityswitchesoccurduringthe
current ramp, leading to an exponential tail of the distribution (shown in green), quantifying τ . The I (t) current ramp is
p bias
represented by a dark gray line. (c) Experimental dataset in the slow limit. Note the change in the current- and timescale
compared to panel (a). We show the exponential cutoff in green, and extract τ = 49s (solid black line). (d) Experimental
p
data at different temperatures show the temperature dependence of τ . (e) τ as a function of temperature for non-shielded
p p
device N, and shielded devices S1, S2. For detailed comparison, see the main text and the supplementary material. All CPTs
exhibitanactivatedbehaviorwith∆≈170...210µVinthehightemperaturelimitcorrespondingtothegapofthealuminium
leads. Saturation of device N without shielding and no quasiparticle traps is observed below T ≈100mK. Shielded devices S1
and S2 exhibit a minigap-activated behavior ∆(cid:63) ≈20µV in the low temperature limit. The fitted τ (T) function is defined in
p
the main text. Star symbol shows τ =15s at T =12mK extracted from parity distilled data for device S2 (see Fig. 3d).
p
barriers [20]. current from zero (non-dissipative state) to beyond the
switchingcurrent. Here,intheresistivestate,quasiparti-
We extract a charging energy E ≈ 50µeV from the
c cle tunneling causes a random reinitialization of the par-
measuredchargestabilitydiagram. Fordifferentdevices,
ity state of the CPT for the next measurement. This re-
we estimate E ≈ 30...50µeV from the superconduct-
J sultsintheapparent1e periodicityinFig.1c. Neverthe-
inggapsandnormalstateresistancesofthejunctions[21]
less, as long as the parity remains constant during each
assumingequalresistancesforthetwotunnelbarriers. A
sweep, we expect to find the two branches as a bimodal
detailed list of parameters and characterization methods
histogram,asweindeedobserveinFig.2a. Inthesemea-
arepresentedinthesupplementarymaterial. Ourdevices
surements, the current ramp time is much shorter than
are in the intermediate coupling regime with E ∼ E ,
J c the parity lifetime, τ (fast measurement limit).
where the energy diagram (Fig. 1b) and the critical cur- p
rent (Fig. 1d) are sensitive to the charge parity. It is im-
We quantify τ in the slow measurement limit. In
portant to note that our CPTs are in the optimal regime p
this regime parity switches occur during the current
to establish flux-controlled braiding of Majorana bound
ramp (Fig. 2b lower panels) such that reaching the up-
stateswithE ∼E (cid:29)k T [10]andhenceausefulplat-
J c B per branch (depicted as blue in Fig. 2a and 2b) be-
formtoestablishtheparitylifetimeforMajoranacircuits
comes exponentially suppressed (Fig. 2c). The expo-
[22].
nential tail represents parity switches during the cur-
We model the CPT as a two level system which can rent bias ramp, resulting in an observable decay of the
exist in either parity state (red and blue bands in Fig. 1, upper branch (depicted as green in Fig. 2b and 2c),
respectively), and switches state on the timescale of τ p (t) = p (0)exp(−t/τ ). Thus, from the decay of the
p u u p
[23]duetoquasiparticletunneling. Wecollecttheswitch- histogram (black solid line in Fig. 2c), we can directly
ing current histograms by repetitively sweeping the bias obtain τ .
p
3
The observed τ is a result of single electron tunneling
p a b
1 2 3 3
events through the junctions of the CPT. In the zero I 1
vsletoaaldttaessg[e2o4ns]tta(hftoeer,isdwleaetnadcilasannsedlienttkhheeτpqsuutapospitlpehamertesincutlbeagrdyaepnmsdaiettynersiiinatyl)t:hoef IVbiga(st()t)I0 twait swng I/Ic c,max0.5
V (t)
sd 1 2
2n ρ
τ−1 = qp subgap, (1) -2 -1 0 1 2
p e2RNρAlρNbTiN time 10 20 ng
c Counts d
1.0
whereR isthenormalstateresistanceoftheCPT.Itis
N
instructive to note that the parity lifetime is determined Fp0.8
bnriyoamlt.heAenosqsluouagmsiciipanalgrDtaiyctlnheeedsrempnaasrlitanymient(eTtrh)e[∝2l5e]√adoTsfe[t2xh2pe](ia−snl∆adntdh/emkpahtTee)-- I(nA)sw2.0 Fidelity,00..64
qp Al B
in the leads, we find ∆ = 170...210µeV (Fig. 2e) 1.0 0.2
Al
for temperatures exceeding 120mK, in good agreement 0
-2 0 2 10-1 1 10 102
with the superconducting gap of the aluminium leads n wait time, t (s)
g wait
extracted from the charge stability diagram. We can
therefore attribute the observed parity lifetime for T > FIG. 3. Parity state distillation. (a) Schematic cur-
120mK to the thermal quasiparticle population in the rent bias and gate voltage waveforms applied to the device.
leads. First, current bias pulse with an amplitude between the two
branchesisapplied(1). Atthesametimethemeasuredvolt-
FordeviceN,however,wefindasaturatedτ =9.5ms
p age V (t) is recorded to initialize the parity state. Then the
in the low temperature limit, a common observation in sd
gatevoltageisramped(2)andfinally,theswitchingcurrentis
superconducting qubits [4] and hybrid single electron
recorded(3). (b)Theschematicrepresentationoftheapplied
transistors [24] signifying the presence of non-thermal waveformsoverlayedontheparity-dependentcriticalcurrent.
quasiparticle excitations. (c)Paritydistilledswitchingcurrenthistogramexhibiting2e
periodicitywitht =100ms. (d)Paritydistillationfidelity
Wefurtherimprovethelowtemperatureparitylifetime wait
asafunctionoft ,seemaintext. Solidredlinedenotesthe
by introducing microwave-tight shielding coated with in- wait
fit∼exp(−t /τ )withτ =15s. Alldatawasrecordedon
wait p p
frared absorber painting and Ti/Au quasiparticle traps
device S2.
for devices S1 and S2. These additions result in a non-
saturated behaviour of τ , and we observe a minigap ac-
p
tivated behaviour with ∆(cid:63) ≈20µeV for both devices. It by defining the fidelity as:
is to be stressed that this observation signals that the
p −p
effective quasiparticle temperature of the CPT follows F = u,f u,i, (2)
p 1−p
the bath temperature down to the 10mK regime. We u,i
find τ = 49s at T = 12mK for device S2. To put
p where p is the conditional probability of the upper
u,f
this number into context, we note that the Josephson
branch in the final step (3), and p is the initial prob-
u,i
frequency f =E /h≈10GHz and thus a single quasi-
J J ability. We note that the above expression is valid for
particle event occurs only once for every τ f ∼ 1011
p J an arbitrary 0<p <1 value set by the average quasi-
u,i
Cooper pairs tunneling through the junctions. This sig-
particle occupation of the CPT. For device S2 we find
nifies the low probability of parity switches for an open
F = 0.88±0.05 for t = 100ms demonstrating the
p wait
device with E ≈E required for flux-tunable Majorana
J c high degree of parity distillation. By changing t be-
wait
braiding schemes.
tween the parity initialization (1) and measurement (3),
Thus far, we started each switching current measure- we acquire an independent measurement τ = 15s for
p
ment from an unknown parity state because of the ran- device S2 at T =12mK (Fig. 3d).
dom reinitialization in the dissipative state of the CPT Finally, we investigate the evolution of τ (B) in differ-
p
for Ibias > Isw. In order to reproducibly select the ent magnetic field directions. In parallel magnetic field,
same parity state, we employ a parity distillation pro- we observe a gradual decrease of τ . The onset of the
p
tocol (Fig. 3) where, by selecting a single parity state steep decay at B = 110mT (yellow arrow in Fig. 4a) is
without switching to the resistive state, we ensure that in agreement with the condition for vortex penetration
the parity remains well defined for the subsequent mea- through a mesoscopic superconducting island [26] with
surement. This protocol indeed results in a 2e periodic Φ ≈ 1.1Φ0 >∼ Φ0. This result underlines the significance
switching current pattern (Fig. 3c) which is observed for of the sample geometry for magnetic field-enabled CPTs
the first time for a non-aluminium CPT. to avoid vortex formation. However, our device exhibits
We quantify the effectiveness of the parity distillation τ >10msinB >100mT,requiredtoinduceMajorana
p (cid:107)
4
measurement data and theoretical expressions of criti-
a
cal magnetic field of thin stripes. We however conclude
1
) S that vortices induced by a perpendicular magnetic field
s
(p S1 B can increase the efficiency of quasiparticle traps, but the
τ M formation of a vortex phase in the near vicinity of the
,
e CPTenhancesquasiparticletransportinagreementwith
m T=12mK
ti earlier observations [28, 29].
e
y lif10-1 [8 ] [7 ] [9 ] CoIonpceor-npcaluirsitorna,nwsiestfoarbsrsichaotweidnganpdarcihtyareaffcteecrtiszefodrNabnToinN-
t
ri B aluminium superconductor for the first time. We char-
a
P acterize the parity lifetime by evaluating the switching
currenthistogramsandfindvaluesexceeding1minuteat
10-2 T =12mK. Our devices are in the regime of Ej ∼Ec (cid:29)
0 50 100 150 k T ideal for Majorana braiding schemes. Furthermore,
B
B (mT)
b II wedemonstratechargeparitydistillationtoreproducibly
initialize the island in a given parity state. We find par-
102 itylifetimesinexcessof10msinexternalmagneticfields
) up to 150mT and showed the importance of sample ge-
s
( S2 ometry for magnetic field-enabled operation required for
p
τ, 10 inducing Majorana bound states.
e
m T=12mK The authors thank A. R. Akhmerov, S. Rubbert,
ti Y.Nazarov,R.LutchynandJ.Pekolaforfruitfuldiscus-
e
f B sions and R. N. Schouten for technical assistance. This
li 1
y work has been supported by the Netherlands Founda-
t
ari tion for Fundamental Research on Matter (FOM) and
P Microsoft Corporation Station Q. A. G. acknowledges
10-1 funding from the Netherlands Organisation for Scientific
Research (NWO) through a VENI grant.
0 10 20
D. J. W. fabricated the devices. D. J. W. and
B (mT)
┴ A.G.performedthemeasurements. D.J.W., A.G.and
L. P. K. discussed the data, contributed to the analysis
FIG. 4. Influence of the magnetic field on the CPT. and wrote the manuscript.
(a)Theparitylifetimeasafunctionofthein-planefield,B
(cid:107)
pointing as shown in the inset. The shaded region depicts
the condition for inducing Majorana bound states (MBS) in
spin-orbit coupled semiconductor wires [7–9]. The change in
slope at B ≈110mT is denoted by the yellow arrow and the
[1] D. Averin and Y. Nazarov, Phys. Rev. Lett. 69, 1993
dashlineservesasaguidetotheeye. (b)Theparitylifetime
(1992).
asafunctionofperpendicularfield,B . Thedashlineshows
⊥ [2] P. Lafarge, P. Joyez, D. Esteve, C. Urbina, and M. H.
the overall trend. The inset shows the electron microscope
Devoret, Nature 365, 422 (1993).
image of the device with the white scale bar denoting 5µm.
[3] J. Clarke and F. K. Wilhelm, Nature 453, 1031 (2008).
[4] D. Riste, C. C. Bultink, M. J. Tiggelman, R. N.
Schouten, K. W. Lehnert, and L. DiCarlo, Nat Com-
bound states [7–9]. mun 4, 1913 (2013).
In contrast, applying a perpendicular field first results [5] J. Alicea, Reports on Progress in Physics 75, 076501
(2012).
in an increase of τ reaching a maximum value τ =94s
p p [6] N. Read, Phys. Today 65, 38 (2012).
atB ≈10mT,beforedroppingathighermagneticfields
⊥ [7] R.M.Lutchyn,J.D.Sau, andS.DasSarma,Phys.Rev.
(Fig. 4b). Making use of the relation between the lower
Lett. 105, 077001 (2010).
critical field and the stripe width, Bc1(w) ∼ Φ0/w2 [27] [8] Y.Oreg,G.Refael, andF.vonOppen,Phys.Rev.Lett.
we attribute the initial increase to vortex formation and 105, 177002 (2010).
hence more effective quasiparticle trapping in the wide [9] V. Mourik, K. Zuo, S. M. Frolov, S. R. Plissard, E. P.
lead sections (w ≈ 2µm) of the device (see wide light A. M. Bakkers, and L. P. Kouwenhoven, Science 336,
1003 (2012).
gray sections in Fig. 4b). Upon reaching B ≈ 10mT,
[10] T. Hyart, B. van Heck, I. C. Fulga, M. Burrello, A. R.
the vortex phase becomes stable in the close vicinity of
Akhmerov, and C. W. J. Beenakker, Phys. Rev. B 88,
the CPT (w ≈250nm) causing a gradual decrease of τ .
p 035121 (2013).
We note that due to ξAl ≈ 100nm ∼ w for our devices, [11] M. T. Tuominen, J. M. Hergenrother, T. S. Tighe, and
we cannot make a quantitative comparison between our M. Tinkham, Phys. Rev. Lett. 69, 1997 (1992).
5
[12] T. Eiles, J. Martinis, and M. Devoret, Phys. Rev. Lett. 486 (1963).
70, 1862 (1993). [22] D. Rainis and D. Loss, Phys. Rev. B 85, 174533 (2012).
[13] P. Joyez, P. Lafarge, A. Filipe, D. Esteve, and M. H. [23] R. M. Lutchyn, L. I. Glazman, and A. I. Larkin, Phys.
Devoret, Phys. Rev. Lett. 72, 2458 (1994). Rev. B 74, 064515 (2006).
[14] L. J. Geerligs, V. F. Anderegg, J. Romijn, and J. E. [24] O.-P. Saira, A. Kemppinen, V. F. Maisi, and J. P.
Mooij, Phys. Rev. Lett. 65, 377 (1990). Pekola, Phys. Rev. B 85, 012504 (2012).
[15] M. D. Shaw, R. M. Lutchyn, P. Delsing, and P. M. [25] R.Dynes,V.Narayanamurti, andJ.Garno,Phys.Rev.
Echternach, Phys. Rev. B 78, 024503 (2008). Lett. 41, 1509 (1978).
[16] R. Dolata, H. Scherer, A. B. Zorin, and J. Niemeyer, [26] V.V.Moshchalkov,L.Gielen,C.Strunk,R.Jonckheere,
Journal of Applied Physics 97, 054501 (2005). X. Qiu, C. V. Haesendonck, and Y. Bruynseraede, Na-
[17] A. M. Savin, M. Meschke, J. P. Pekola, Y. A. Pashkin, ture 373, 319 (1995).
T.F.Li,H.Im, andJ.S.Tsai,AppliedPhysicsLetters [27] G. Stan, S. B. Field, and J. M. Martinis, Phys. Rev.
91, 063512 (2007). Lett. 92, 097003 (2004).
[18] J. J. Toppari, T. Kühn, A. P. Halvari, J. Kinnunen, [28] J.T.Peltonen,J.T.Muhonen,M.Meschke,N.B.Kop-
M. Leskinen, and G. S. Paraoanu, Phys. Rev. B 76, nin, and J. P. Pekola, Phys. Rev. B 84, 220502 (2011).
172505 (2007). [29] C. Wang, Y. Y. Gao, I. M. Pop, U. Vool, C. Axline,
[19] J. Halbritter, Applied Physics A 43, 1 (1987). T. Brecht, R. W. Heeres, L. Frunzio, M. H. Devoret,
[20] W.D.OliverandP.B.Welander,MRSBulletin38,816 G. Catelani, L. I. Glazman, and R. J. Schoelkopf, Nat
(2013). Commun 5, 5836 (2014)
[21] V. Ambegaokar and A. Baratoff, Phys. Rev. Lett. 10,
1
Supplementary online material
1 minute parity lifetime of a NbTiN Cooper-pair box
DEVICE FABRICATION
The Cooper-pair transistors (CPTs) were fabricated using electron beam lithography and thin film deposition
starting with a p++ doped silicon wafer with a 285nm thick thermally grown SiO surface layer. First, aluminium
2
leadsweredefinedandevaporatedinahigh-vacuumchamber(p ∼10−7Torr)atarateof0.2nm/swithathickness
base
of 30...35nm. Subsequently, the mask for the NbTiN island was defined in a second lithography step. The sample
wasloadedintoanultrahighvacuumAJAInternationalATC1800sputteringsystem(p ∼10−9Torr),wherefirst
base
a ∼5nm Al layer was removed by means of argon plasma etching at p=3mTorr. This step was followed by in-situ
oxidization to create AlO tunnel barriers. Without breaking vacuum, the NbTiN island was then sputtered with a
x
layer thickness of 70...100nm.
We used a Nb Ti target with a diameter of 3(cid:48)(cid:48). Reactive sputtering resulting in nitridized NbTiN films was
0.7 0.3
performed in an Ar/N process gas with a typical 10at% nitrogen content at a pressure of 3mTorr using a DC
magnetronsource. Duringdeposition, a−45Vbiaswasappliedtothesamplewithrespecttothetarget. Thecritical
temperatureofthesuperconductingtransitiontemperatureofthinfilmswithalayerthicknessof100nmwasmeasured
to be 14.1K in zero magnetic field.
For the shielded samples S1 and S2, quasiparticle traps were fabricated by first cleaning the Al surface by means
of argon plasma milling at p=0.2mTorr and in-situ evaporation of 25nm Ti and 100nm Au films at a base pressure
of ∼10−7Torr (see Fig. S1c and d).
Care was taken to remove resist mask residues after each electron beam writing step using a remote oxygen plasma
etch with a pressure of 1mbar.
device island size junction size NbTiN thickness traps oxygen exposure R
N
(nm×nm) (nm×nm) (nm) (Torr×s) (kΩ)
N 500 × 500 200 × 200 70 no 7400 58
S1 450 × 200 200 × 200 100 yes 150 125
S2 450 × 250 200 × 250 100 yes 150 66
TABLE S1. Device fabrication parameters of the CPTs discussed in the main text.
MEASUREMENT SETUP
ThemeasurementswereperformedinaLeidenCryogenicsCF-1200drydilutionrefrigeratorwithabasetemperature
of 12mK equipped with Cu/Ni shielded twisted pair cables thermally anchored at all stages of the refrigerator.
Fig.S2ashowstheschematicsofthemeasurement. Thecurrentbiasandgatevoltagewereappliedthroughbattery
operated and optically isolated sources in order to reduce line interference. Similarly, the first stage of the V
sd
amplifier was isolated from the commercial readout electronics. Filtering of the measurement lines was achieved by
room temperature LC π filters with a cutoff frequency of ∼ 100MHz followed by a sequence of a high frequency
copper powder filter [30] and a two-pole RC filter with a nominal f = 50kHz, both thermally anchored to the
−3dB
12mK stage.
Specialcarewastakentoavoidstraymicrowaveradiationbyusinganouterandaninnercoppershieldenclosingthe
device. TheinnersurfaceofbothshieldswastreatedwithcommerciallyavailableAeroglazeZ306paint[31]absorbing
far infrared stray radiation [32]. We note that the inner shield was not present for device N.
A typical DC V −I trace of device S2 at 12mK temperature is presented in Fig. S2b exhibiting a sharp transition
between the dissipationless and the resistive state at the switching current, I . We observe a retrapping current
sw
I (cid:28) I characteristic to unshunted Josephson junctions in the low temperature limit [33]. The additional features
r sw
in the resistive state are consistent with Fiske steps [34].
TheswitchingcurrenthistogramswereacquiredusingaRigolDG4062arbitrarywaveformgeneratorcontrollingthe
isolated current bias source with a triangle wave signal resulting in a dI/dt current ramp. A finite voltage response
above the preset V ∼ 10µV triggers the recording of I (Fig. S2c). We note that the delay of the low pass filters
ref sw
wereaccountedforonthebasisofcircuitsimulations. SubsequentI measurementsweretakenwithsettingzeroI
sw bias
2
a b
c d
FIG. S1. Scanning electron microscope images of the CPTs. (a) Non-shielded device N without quasiparticle traps.
(b), (c), (d) Shielded device S2 featuring quasiparticle traps. Colour legend: dark red: Si/SiO substrate; light blue: NbTiN
2
island, green: aluminium leads and yellow: normal metal (Ti/Au) gate and quasiparticle traps. Scale bars denote 500nm (a),
1000nm (b), 5µm (c) and 200nm (d), respectively.
for approximately 100ms in between to avoid overheating effects. We did not observe a difference in the switching
current histograms taken with waiting times in the range of 20ms and 10s.
BASIC CHARACTERIZATION OF THE CPT
In Fig. S3a we present a typical charge stability diagram of the CPT. First, we establish the superconducting gap
of the aluminium lead and NbTiN island by finding the onset of quasiparticle transport (Fig. S3b and c).
device ∆ ∆ R E E E /E E /E
Al NbTiN N J c J c J c
(µeV) (µeV) (kΩ) (µeV) (µeV) calc. I
sw
N 210 1390 58 54 50 1.08 1.25
S1 218 1420 125 21 62 0.34 0.32
S2 220 1300 66 48 49 0.98 1.16
TABLE S2. Device transport parameters.
It is important to note that we find a finite subgap conductance at eV < 2∆ which is consistent with
sd NbTiN
the presence of the subgap quasiparticle states justifying the analysis leading to equation (1) in the main text.
3
V
a
sd
b
1.0
I
bias
V )
V
g
m
π π π π π (0.0
filte filte filte filte filte Vsd I
r r r r r T sw
room -1.0
-2.0 0.0 2.0
T
I (nA)
MC bias
C C C Outer C C
u u u u u
pow pow pow shield pow pow c I
de de de de de sw
r filter r filter r filter r filter r filter dI
dt
tw tw tw tw tw
o po o po o po o po o po Ibias(t)
le le le le le
R R R Inner R R V
C filte C filte C filte shield C filte C filte Vsd(t) ref
rs rs rs rs rs
time
FIG. S2. Measurement electronic setup and typical waveforms. (a) Schematics of the measurement. (b) Typical
experimentalV −I traceexhibitingawell-definedswitchingcurrent,I . (c)Currentramp(red)withaslopeofdI/dtprobing
sw
I which is recorded when the measured V (blue) reaches V ∼10µV.
sw sd ref
a b c
500 I (pA) 40
100 100 0.1
250
V (µV)sd 0 110 I (pA) 0 0 ( )2dI2ehdV I (nA) 0 0.1 ( )2dI2edVh
-250 0.1 -100 -0.1
-500 -40 0
0 50 -500 -250 0 250 500 -4 -2 0 2 4
V(mV) V (µV) V (mV)
g sd sd
FIG. S3. Basic characterization of the CPT. (a) Stability diagram: log|I| as a function of V and V . We estimate E
sd g c
based on the characteristic resonances (see text). (b),(c) I−V (black) and dI/dV (red) line traces on the scale of ∆ and
Al
∆ , respectively. All data was taken for device S1.
NbTiN
Furthermore, we observe reduced ∆ ≈ 1.3...1.4meV values compared to that of bulk films (∆ > 2meV) [35],
NbTiN
which we attribute to the chemical interaction between the AlO tunnel barrier and the NbTiN film. Indeed, it was
x
shown earlier that the critical temperature of Nb films is particularly very sensitive to contamination with oxygen
[36, 37]. However, the nitridized NbTiN compound is presumably less prone to oxidization [38].
We evaluate the Josephson coupling for a single tunnel junction [39]:
(cid:115) 
¯h ∆ (cid:18) ∆ (cid:19)2
EJ = 2e2R A/l2K 1− ∆ Al  (S1)
N NbTiN
with K(x) being the complete elliptic integral of the first kind. This expression is valid in the zero temperature limit,
4
assuming symmetric tunnel junctions of the resistance of R /2.
N
We estimate the charging energy, E = e2/2C, based on the periodicity of characteristic resonances visible for
c
eV ≤2∆ (Fig. S3a) [40, 41].
sd Al
Alternatively, we can estimate the E /E ratio based on the modulation of I as a function of the gate charge, n
J c sw g
(lastcolumnofTableS2)[42]. WefindagoodagreementbetweentheE /E valuesacquiredbythetwoindependent
J c
methods.
EVALUATION OF THE PARITY LIFETIME
400nA/s
102
100nA/s
T=50mK
s
t
n 10
u
o
C
1
4 2 3 4
I (nA)
sw
FIG.S4. MeasuredswitchingcurrenthistogramsatdifferentdI/dtramprates. Colourlegend: red: dI/dt=100nA/s,
black: dI/dt=400nA/s. The data was acquired on a CPT similar to device N.
Wecheckedtherobustnessoftheextractedparitylifetimeagainstchangingthecurrentramprate. Typicaldatasets
are shown in Fig. S4, giving τ = 1.2ms and τ = 0.98ms for dI/dt = 100nA/s (red) and dI/dt = 400nA/s
p p
(black), respectively. We estimate the typical uncertainty to be 15%, concluding that τ does not depend on dI/dt
p
which validates the analysis in the main text. However, we do not discuss here the intrinsic peak shapes of the
bimodal switching current histogram. Since fast gate charge noise influences the measured distribution [43], we
cannot distinguish between thermally activated [44] and macroscopic quantum tunneling behaviour [33, 45].
We now turn to the temperature dependence of τ . In order to get equation (1) in the main text, we assume the
p
following:
i) The superconducting gap of the island (∆NbTiN >∼ 1.3meV) is much higher than the effective thermal energy
describing the quasiparticle population and the gap of the leads (∆ ≈200µeV).
Al
(cid:112)
ii) ThedensityofstatesintheleadsisBCS-type: ρ (E)=ρ ×|E|/ E2−∆2 for|E|>∆ andzerootherwise.
lead Al Al Al
iii) There is a constant, finite subgap density of states ρ for energies below ∆ in the island.
subgap NbTiN
iv) the energy dependence of the single electron tunnel probability is negligible over the energy range of ∼∆ ,
NbTiN
meaning that the tunnel barrier is much higher than ∆ .
NbTiN
v) The tunnel barriers are identical, each characterized by half the normal state resistance of the full device, R .
N
Considering only single electron tunneling and zero voltage bias across the tunnel barriers, following [46], we get
the quasiparticle tunnel rate:
2 ρ (cid:90) ∞ 2n ρ
τ−1 = subgap ρ (E)f(T,E)dE = qp subgap (S2)
p e2(R /2)ρ ρ lead e2R ρ ρ .
N Al NbTiN 0 N Al NbTiN
5
Assigning an effective temperature to the quasiparticle population in the leads, we find:
(cid:90) ∞
nqp(T)=2 ρlead(E)f(T,E)dE =ρAl(cid:112)2πkBT∆Ale−k∆BATl (S3)
0
in the limit of k T (cid:28) ∆ . For temperatures exceeding 100mK, we assume that the quasiparticle population is in
B Al
thermal equilibrium, and therefore the lattice temperature is equivalent to the effective quasiparticle temperature:
√
τ−1(T)∝ T exp(−∆ /k T).
p Al B
We verify this picture by fitting the observed parity lifetimes with ∆ as a free parameter, and find values ranging
Al
170...210µeV for different devices in good correspondence with the gap determined by voltage bias spectroscopy
(∆ in Table S2).
Al
Notably, the ratio ρsubgap/ρNbTiN is the Dynes parameter [47] of the island material, characterized to be <∼ 10−3
based on measurements of highly resistive single junctions. With this value and using ρ =1.45×1047J−1m−3 [46],
Al
we get n ∼3µm−3 for device N based on the observed parity lifetime of 9.5ms in the low temperature limit.
qp
We now comment on the observed ∆(cid:63) ≈20µeV activation energy observed for devices S1 and S2. We estimate the
maximal even-odd energy difference to be δE ≈ 20...30µeV based on E ≈ E ≈ 50µeV [48] which is in range of
J c
the experimentally observed ∆(cid:63). Similar, activated behaviour of the parity lifetime scaling as ∼ exp(δE/k T) was
B
reported earlier [49].
Providing another possible explanation, we note that a grain size of ≈ 50nm can lead to a level spacing of the
order of 10µeV which can influence single electron transport and hence τ if the grains are weakly coupled, i. e. for
p
disorderedsuperconductingfilms[50]. Disorder-inducedfluctuationsmayalsoexplainthebroadeningofthecoherence
peaks (Fig. S3c) [51, 52].
SUPERCONDUCTING THIN FILM CHARACTERIZATION AND MAGNETIC FIELD DEPENDENCE
Next,weconsiderthepropertiesofsuperconductingstripeswithlayerthicknessd,andawidthwtofindtheLondon
penetration depth λ and the coherence length ξ. We characterize the upper critical field in the parallel (B ) and
L c(cid:107)
perpendiculargeometry(B )basedonthedI/dV tracesofthetunneljunctionsoftheCPT.Inaddition,wemeasure
c⊥
the normal state resistivity of the films that gives an estimate for the mean free path, l [53].
m
First, we establish the length scales of the island material, NbTiN. We find films superconducting at B = 9T
⊥
which leads to an upper limit of ξ <6nm following [54]:
NbTiN
Φ
B = 0 . (S4)
c⊥ 2πξ2
Thepenetrationdepthcanbeestimatedusingthenormalstateresistivityofρ=98µΩcmandthecriticaltemperature
of T =14.1K using the following semi-empirical formula [35]:
(cid:115)
ρ[µΩcm]
λ = ×105nm≈280nm. (S5)
NbTiN T [K]
c
Next we estimate length scales of the Al leads based on the electronic transport through the CPT. Typical thin Al
√
films are type-II superconductors in the dirty limit (l <ξ ) with a reduced coherence length of ξ ≈0.85 ξ l and
m 0 0 m
(cid:112)
withaLondonpenetrationdepthofλ≈λ ξ /l ,whereξ ≈1500nmandλ ≈16nmarethebulkvalues[54]. For
0 0 m 0 0
our films, we estimate l ≈ 8.5nm based on the resistivity of ρ = 4.3µΩcm [53]. From the stability diagram of the
m
devices, weextractuppercriticalfieldsofB =36.4±4mT(Fig.S5d)andB =320±10mT(Fig.S5b)leading
c2,⊥ c2,(cid:107)
to a coherence length of ξ = 96nm and λ = 230nm which enables vortex formation in the aluminium leads in
Al Al
perpendicular magnetic field.
It is important to observe that ξ (cid:28) d ≈ 100nm enables vortex formation for an in-plane geometry in the
NbTiN
NbTiN island. We find a characteristic suppression of τ at B =70mT for device S2 (orange dots in Fig. S5a) and
p (cid:107)
atB =110mTfordeviceS1(cyandotsinFig.S5a). Consideringtheeffectivecross-sectionalareas(seeTableS1for
(cid:107)
dimensions), wefind Φ≈1.5Φ andΦ≈1.1Φ forS2andS1, respectively, whichisinqualitativeagreementwiththe
0 0
threshold of a single vortex formation in a mesoscopic island [55–57]. We also note that B of the leads (Fig. S5b)
c2,(cid:107)
does not depend on the direction of B , therefore the different evolution of τ can only be explained by the different
(cid:107) p
alignment of B with respect to the NbTiN islands.
(cid:107)